在役预应力混凝土桥梁损伤状态承载力评估
2016-09-12姜天华武汉科技大学城市建设学院湖北武汉430070
姜天华,王 强,杨 壮,黄 雯(武汉科技大学 城市建设学院,湖北 武汉 430070)
在役预应力混凝土桥梁损伤状态承载力评估
姜天华,王强,杨壮,黄雯
(武汉科技大学 城市建设学院,湖北 武汉430070)
首先介绍了桥梁冗余度评价指标,而后采用有限元软件MIDAS/Fea对一座在役预应力混凝土连续刚构桥进行实体单元建模,采用调整张拉预应力值、截面开裂的方法来模拟损伤桥梁,并对完好桥梁、预应力损失桥梁和跨中截面损伤桥梁进行材料非线性分析,得到相应的荷载-位移曲线,依据桥梁冗余度评价指标对桥梁的承载能力进行评估。结果表明:在评估在役预应力混凝土桥梁损伤状态承载力方面,桥梁冗余度评估理论可对造成桥梁损伤的因素进行定量分析,并为在役预应力混凝土桥梁的损伤评判和加固提供理论基础。
预应力混凝土;连续刚构桥;冗余度;有限元法;桥梁评估
在役大跨预应力混凝土箱梁桥在运营过程中,经常出现梁体开裂及跨中持续下挠等病害,随着时间的推移,桥梁承载力冗余度将大幅度下降,最终造成桥梁严重安全隐患。目前,国内外基于冗余度理论对框架结构的抗震倒塌能力的评估分析较多,而对桥梁的冗余度评估相对较少,而且在我国公路桥梁设计规范中还未涉及到预应力混凝土桥梁冗余度的计算,仅有一些根据桥梁冗余度理论对双箱结合梁桥的评估[1-2]。本文基于冗余度理论对在役预应力混凝土连续刚构桥损伤状态承载力进行评估,即采用预应力损失、截面开裂的方法来模拟损伤桥梁[3-5],运用有限元软件MIDAS/Fea对损伤桥梁进行材料非线性分析,结合桥梁冗余度评估理论[6-10]对损伤桥梁承载力进行定量分析,为其他桥型损伤状态承载力的评估提供相应基础。
1 桥梁冗余度评价指标
桥梁冗余度是桥梁结构在局部构件损伤的情况下,桥梁系统继续承载的能力。由于冗余度关系到系统的行为,为了弥合单个构件的设计与系统作用之间的差距,美国联合公路项目(NCHRP)报告406中引入了可以评估桥梁构件冗余度水平的系统因数:LF1,LFu,LFf,LFd,4种因素分别对应4种状态:构件破坏、承载能力极限状态、功能极限状态和损伤极限状态。构件破坏:此时,用弹性分析的方法检查独立构件是否安全以及其名义承载力,用荷载系数LF1表征桥梁结构在构件失效前的承载力。承载能力极限状态:桥梁或桥梁构件达到极限承载能力或不能继续承载的状态,用荷载系数LFu来表征桥梁结构达到极限状态时的承载力。功能极限状态:桥梁损伤导致其某一功能不能满足设计规范的特定状态,用荷载系数LFf表征使损伤桥梁挠度达到L/100时的承载力,其中L是跨长。损伤极限状态:桥梁系统中承重构件损伤后的极限承载能力状态,用荷载系数LFd来表征损伤桥梁结构达到极限状态时的承载力。通过LFu,LFf,LFd分别与LF1的比值可以得到桥梁的承载力极限状态、功能极限状态和损坏极限状态的强度储备率Ru,Rf和Rd。NCHRP报告406指出一个桥梁系统被认为有充足的冗余度,要求Ru≥1.30,Rf≥1.10和Rd≥0.5。即承载力极限状态下冗余度需求比ru=LFu/1.3、功能极限状态下冗余度需求比rf=LFf/1.1、损伤极限状态下冗余度需求比rd=LFd/0.5,三者均≥1。在桥梁结构中,符合规范要求的桥梁本身存在的构件强度储备比 r1应等于1,但是实际上桥梁通过设计提供的构件强度储备比r1将大于1。其中

式中:LFreq为桥梁抗弯承载能力荷载系数;MD为恒载作用下的弯矩;Rreq为正截面抗弯弯矩;ML为车辆荷载作用下的弯矩。
最终可得到桥梁冗余度评价指标Φreq为

桥梁冗余度评价指标 Φreq的数值不应小于1,否则该损伤桥梁由于没有足够的冗余度而发生倒塌的可能性极高;同时,桥梁冗余度指标Φreq的数值越大则表明该损伤桥梁抵抗倒塌的能力越高。
2 空间有限元建模
以一座预应力混凝土连续刚构桥作为研究对象。该桥主桥为(57.5+95.0+57.5)m三跨一联的连续刚构;主梁采用单箱单室截面形式,箱梁宽度为6.7 m,箱梁两边的翼板悬臂长度为 2.65 m,全桥宽度为12 m。采用有限元软件MIDAS/Fea进行分析,建立实体单元模型如图1所示。成桥阶段有限元模型共划分为37 672个四面体单元,12 829个节点,同时模拟预应力钢筋的作用,预应力钢筋用杆单元建立,然后划分成138个预应力钢筋单元。

图1 桥梁有限元模型
3 桥梁材料非线性分析
本文在桥梁材料非线性分析中,混凝土采用总应变裂缝模型中的转动裂缝模型[11]。裂缝方向随着主应变的方向发生变化。下述完好桥梁指桥梁材料参数都按设计值取值,其中C50重度取25 kN/m3,弹性模量3.45×104MPa,泊松比0.2。预应力钢筋弹性模量1.95×195MPa,顶板张拉力3 098.9 kN,底板张拉力2 916.8 kN。假定纵向预应力损失10%,20%,30%,40%,其中预应力损失是以完好桥梁中张拉预应力初始值为基础。将主梁跨中梁底相应位置处节点分割,以期实现主梁横向开裂,其中横向裂缝的长度,按跨中梁底宽度的10%,20%,30%进行模拟。
3.1完好桥梁分析
采用有限元MIDAS/Fea对完好桥梁进行材料非线性分析,可得到中跨加载时荷载-位移曲线(见图2)。由图2的荷载-位移曲线可得 LF1=24和 LFu= 38。通过有限元软件MIDAS/Civil对该桥进行线性分析可得到完好桥梁恒载作用下的中跨跨中截面弯矩MD=22 377.9 kN·m和车辆荷载作用下桥梁中跨跨中截面的弯矩ML=12 684.7 kN·m,并且根据桥梁使用阶段正截面抗弯验算结果得到桥梁中跨跨中正截面抗弯承载能力Rreq=123 971.8 kN·m。

图2 完好桥梁跨中荷载-位移曲线
桥梁中跨跨中截面抗弯承载力荷载系数

桥梁结构构件强度比
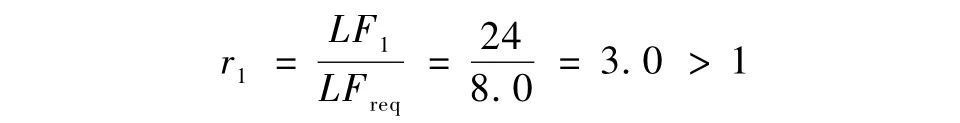
3.2截面开裂后的冗余度计算
分别对截面开裂长度为梁底宽度 10%,20%,30%的桥梁进行材料非线性分析,并用桥梁冗余度指标对损伤桥梁进行计算分析,可得到完好桥梁和截面开裂后的桥梁中跨跨中荷载-位移曲线(见图3)。然后根据冗余度计算公式可分别计算出截面开裂10%,20%,30%状态下桥梁的冗余度。计算结果如表 1所示。

图3 截面开裂状态下桥梁跨中荷载-位移曲线
由图3的荷载-位移曲线可得 LF1等值。通过有限元软件MIDAS/Civil对损伤桥梁进行线性分析。现以截面开裂长度为梁底宽度10%为例,损伤桥梁恒载作用下的中跨跨中截面弯矩MD=22 262.79 kN·m和车辆荷载作用下桥梁中跨跨中截面的弯矩ML= 12 684.7 kN·m,根据 PSC设计求得桥梁中跨跨中使用阶段正截面抗弯承载能力 Rreq=123 972.094 8 kN·m。
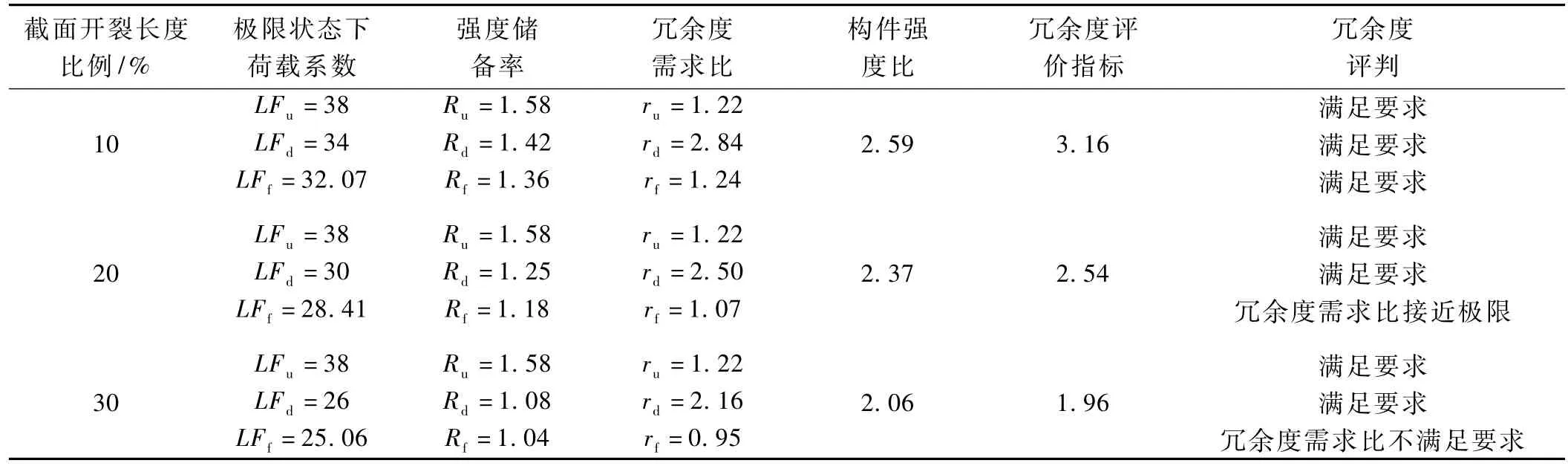
表1 截面开裂状态下桥梁冗余度计算
桥梁中跨跨中截面抗弯承载力荷载系数

桥梁结构构件强度比

由表1可知,当截面开裂长度达到梁底宽度20%时桥梁的冗余度需求比接近极限,在役损伤混凝土桥梁的冗余度指标大约为2.54;如果截面裂缝长度进一步增大,桥梁结构冗余度需求比则不能满足要求,结构承载力达到损伤极限状态,需要对桥梁结构进行加固处理。
3.3预应力损失后的冗余度计算
分别对该桥在预应力损失比例为 10%,20%,30%,40%的状态下进行材料非线性分析,并采用桥梁冗余度指标对损伤桥梁进行计算,可得到完好桥梁和预应力损失后的桥梁中跨跨中荷载-位移曲线(见图4)。然后根据冗余度计算公式可分别计算出预应力损失10%,20%,30%,40%状态下桥梁的冗余度。计算结果如表2所示。
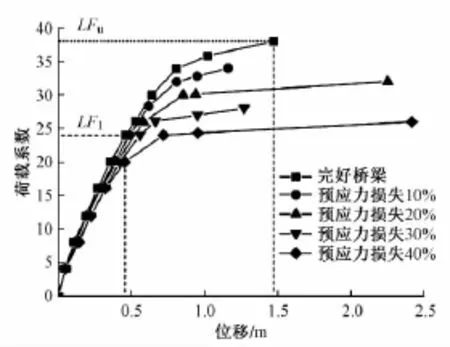
图4 预应力损失状态下桥梁跨中荷载-位移曲线

表2 预应力损失状态下桥梁冗余度计算
由表2中数据可知,当预应力损失达到30%时桥梁的冗余度需求比接近极限,在役损伤桥梁的冗余度指标大约为2.56;如果预应力损失进一步增大,桥梁结构冗余度需求比则不能满足要求,结构承载力达到损伤极限状态,需要对桥梁结构进行加固处理。
将截面开裂和预应力损失2种情况下的冗余度评价指标值绘制图5所示冗余度指标与损失比例变化曲线,可以看出结构截面开裂与预应力损失的比例与桥梁冗余度成线性递减关系,截面开裂对冗余度指标的影响比预应力损失的影响更加显著,说明截面开裂对桥梁结构的安全影响更大。

图5 冗余度指标与损失比例变化曲线
4 结论
1)利用冗余度评价指标可以对有预应力长期损失及截面开裂损伤的桥梁进行定量分析。当截面裂缝长度达到梁底宽度20%、或预应力损失达到30%时,该损伤桥梁的冗余度需求比接近极限,在役损伤混凝土梁桥结构承载力达到损伤极限状态。
2)结构预应力损失和截面裂缝长度比例与桥梁冗余度呈线性递减关系,截面横向裂缝对冗余度指标的影响更加显著,说明截面开裂对混凝土桥梁结构的安全影响更大。
3)桥梁冗余度评价指标不但可以对预应力混凝土连续刚构桥承载力损伤状况进行评价,也可以用于其他桥型的承载能力评价,为在役混凝土桥梁的损伤评判和加固提供理论基础。
[1]左琼.基于冗余度理论的钢筋混凝土框架结构抗地震倒塌能力评估[D].北京:中国建筑科学研究院,2013.
[2]姜勇,苑春艳.双箱结合梁桥结构冗余度评估[J].世界桥梁,2013,41(3):66-72.
[3]赵煜,贺拴海,李春风,等.在役预应力混凝土箱梁开裂后承载力评估[J].同济大学学报(自然科学版),2010,38 (9):1271-1275.
[4]王法武,石雷飞.大跨径预应力混凝土梁桥长期挠度控制研究[J].中外公路,2006,26(4):107.
[5]孙磊,慕玉坤,郝宪武.基于小波分析的PC连续刚构桥损伤识别研究[J].公路工程,2015,40(2):239-243.
[6]尹德兰,邓宇.桥梁设计的冗余度[J].桥梁建设,2013,43 (5):93-98.
[7]GHOSN M,MOSES F.Redundancy in Highway Bridge Superstructures[R]Washington:Transportation Research Board of National Research Council,1998.
[8]KHEDEKAR N C.Redundancy for Steel Highway Bridge Superstructures[D].Cleveland:Case Western Reserve University,1998.
[9]PARK Y,JOE W.An Experimental Study on After-fracture Redundancy of Continuous Span Two-Girder Bridges[J]. International Journal of Steel Structures,2012,12(1):1-13.
[10]GHOSON M,MOSES F,FRANGOPOL D M.Redundancy and Robustness of Highway Bridge Superstructures and Substructures[J].Structure and Infrastructure Engineering,2010,6 (1/2):257-278.
[11]盛康.Midas FEA框架桥非线性裂缝分析[J].铁道勘测与设计,2009(2):52-60.
(责任审编孟庆伶)
Assessment of Bearing Capacity for Damaged Prestressed Concrete Bridge in Service
JIANG Tianhua,WANG Qiang,YANG Zhuang,HUANG Wen
(Institute of Urban Construction,Wuhan University of Science&Technology,Wuhan Hubei 430070,China)
Redundancy evaluation index for bridge was introduced in this paper.A 3D model of a prestressed concrete continuous rigid frame bridge in service was built with solid elements using M IDAS/Fea.T he damages of the bridge were simulated by adjustment of prestress and cracked section.T he undamaged bridge,the bridge with prestress losses and the bridge with cracks at the mid-span were analyzed using non-linear method.T he loaddisplacement curves were obtained.T he bearing capacity was assessed based on redundancy evaluation index.T he results indicate that redundancy theory may be used for quantitative analysis of bridge damage factors.
Prestressed concrete;Continuous rigid frame bridge;Redundancy;Finite element method;Bridge assessment
U441+.4
A
10.3969/j.issn.1003-1995.2016.08.07
1003-1995(2016)08-0031-04
2016-03-05;
2016-05-30
湖北省自然科学基金(2014CFB823);湖北省交通运输厅重点科技项目(2011275)
姜天华(1971— ),男,教授,博士。
