数学符号意识有效生成探究
2016-09-10吴志健
吴志健
数学符号是数学的语言、工具与方法,一般指数字、字母、图形和关系式等。数学符号意识是指在感知、认识、运用数学符号时的一种积极的心理倾向。数学符号意识的有效生成,是指在课堂教学中,通过某个数学活动,使学生对数学符号的引入、理解和运算形成相应的心理反应。这里的“有效”,强调的是学与教的策略合理,数学活动有针对性,心理反应积极。由于“建立符号意识有助于学生理解符号的使用,是数学表达和进行数学思考的重要形式”,因此,培养学生符号意识成为广大教育工作者的一个重要课题。
一、 立足需求,培养数学符号引入意识
数学符号引入意识是指在表示数、数量关系和变化规律时,能比较科学地引入相应的符号来表达。这里主要指引入已知数表示不变量、引入字母表示变量或特定量、引入含有字母的算式表示数量关系和变化规律等。它不仅指初次接触时能在教师引领下引入符号,更指在以后运用所学解决其他问题时能自觉地引入符号。
把生活元素融入主题情境,从情境中引出数学符号,已经成为共识。但符号只有赋予了数学意义,才能成为数学符号,生活中的符号与数学符号常常同形不同义、同形不同法。笔者认为,如果要从生活中引入,还得增添数学化环节,也就是要从数学的发展需要引入数学符号,让数学符号的引入融入到数学发展的需要中。
1.注重表达的需求
实际上,原有的表达和引入符号后形成的新的表达,都有一定的、合理的存在基础。由前者到后者,不仅有学习内容上的转变,而且有学习者心理上的认同。判断引入符号是否成功的维度有两个:一是引入后表述的问题是否更清楚,二是引入后学生能不能感悟到它的必要性。由此不难发现,需要关注表达过程与表达形式的需求。
第一,要让学生自由表达,通过质疑让学生感悟到用符号表达的价值。例如,教学用数对表示物体的位置。当学生从生活经验中的第几排、第几行入手,表达教室里某同学的位置时,产生同一位置有不同的表示方法,很难更方便表达、更准确理解的疑问,从而引出数对。
第二,要让学生通过不同表达形式之间的比较权衡利弊。例如,教学乘法分配律,有的教师怕学生死记硬背,希望他们用自己的语言与方式来表达,故不出示运算律的文字叙述。这样,学生就很难把文字叙述与符号语言进行对比,从而明晰a×(b+c)=a×b+a×c的简洁性。为此,我们可以利用已有经验,强化比较,凸显简洁。譬如,在让学生做简便计算18×27+73×18时,可以提问:你运用了什么运算律?并请学生用语言叙述一下。当学生难以表达清楚时,请他用字母来表示。这样,学生就会在无形中体会数学符号的简洁性。
2.注重思考的需求
从数学思考的过程来看,数学符号的合理引入,有助于压缩思考过程,提高有效性。从数学思考的结果来看,引入数学符号,有助于突出思考结果的本质属性,有利于进行判断与推理、分析与综合。这里的数学思考包含三个内容:首先是引入数学符号的缘由,其次是引入数学符号的过程,第三是根据引入的数学符号来解决相关问题。可见,这种数学思考的需求,必须体现在相应的学与教的过程中。但是在用字母表示公式的教学中,有两种倾向值得关注。一是忽视巩固公式时数学思考上的需求。例如,教学平行四边形面积计算时,教师能注重分层引导学生用字母表示公式,但是在运用公式做习题时,只是让学生指出平行四边形底与相应的高各是多少,而不去引导学生先想一想字母公式。二是忽视在推导新的字母公式时运用已学过的相应的字母公式。例如,在教学三角形面积的计算时,有些教师没有利用平行四边形面积计算的字母公式去引导学生获得三角形面积计算的字母公式。

二、 彰显变化,建立数学符号理解意识
数学符号理解意识是指能阐述数学符号在具体情境中的含义。关于数学符号,对于“教”来讲,其顺序是“引入→理解→运算”;但是对于“学”而言,其顺序是“理解→运算→引入”,或者“理解→引入”。可见,数学符号理解意识直接影响着学生的数学符号引入意识和运算意识,它是学生数学符号意识的重要基石。这里的重点有三:其一,梳理结合具体情境的各种含义;其二,赋予数学符号以具体情境;其三,对数学符号进行更换或者一般化。由此可以看出,建立数学符号理解意识,离不开数学符号形式与含义的变式训练。
1.注重形式的变化
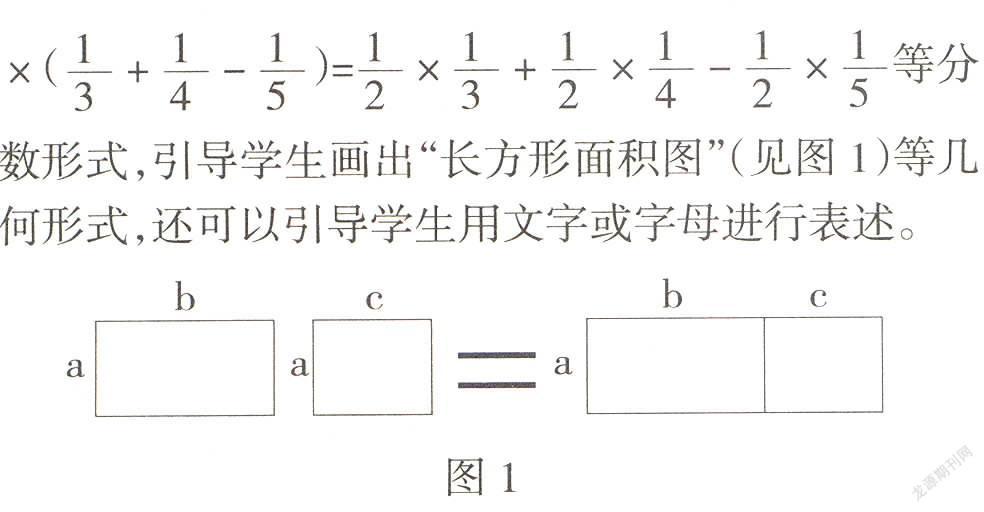
理解数学符号,关键是对其内涵及外延的正确把握,而学生往往受数学符号形式的困扰,难以甄别。因此,若是关系式,就要用各种形式去表示,或具象化,或抽象化。例如,教学乘法分配律。可以引导学生列举25×(16+37)=25×16+25×37等整数形式,4.3×6.1-5.9×4.3=(6.1—5.9)×4.3等小数形式,×(+-)=×+×-×等分数形式,引导学生画出“长方形面积图”(见图1)等几何形式,还可以引导学生用文字或字母进行表述。
若是数,就要变换情境,或序数、或基数、或数量。例如,教学分数的意义,当学生明确的含义后,可以引导学生做以下两道题目。(1)一根木料锯成两段,第一段长米,第二段长,哪一段长一些?(2)有两根同样长的木料,第一根用去米,第二根用去,哪一根剩下的长一些?通过画图、解题,使学生明白题中米和的单位“1”各指的是什么,能不能相同,从而加深对其含义的理解。
同时,也要用字母表示数,或改变取值范围,或更改运算符号。例如,教学公因数与公倍数。先让学生做习题:16÷2=8,16和2的最大公因数是( ),最小公倍数是( )。再引导学生进行抽象,用字母表示数,形成如下题目并解答。(1)a÷b=8(且a、b都是不为0的自然数),a和b的最大公因数是( ),最小公倍数是( )。(2)b=8a(且a、b都是不为0的自然数),a和b的最大公因数是( ),最小公倍数是( )。
2.注重含义的变化
对于数学符号的含义,我们通常让学生在具体的生活情境中获取,导致学生获得的“含义”既具有相对的情境性、初步的独立性,又具有一定的抽象性。即学生头脑里的“含义”可能全部内容都在变化,也可能部分内容在变化。因此,加强“含义”的变式训练,有助于学生建立数学符号理解意识。
第一,要引导学生分析同一个符号的不同含义。例如,教学用字母表示。可以运用下面的题组,帮助学生对a的含义进行对比。(1)摆1个三角形,要用3根小棒;增加1个三角形,共要用5根小棒。那么,增加a个三角形,共要用小棒( )根。(2)摆1个三角形,要用3根小棒;摆2个三角形,要用5根小棒。那么,摆a个三角形要用小棒( )根。其中,第1小题可以填“3+2a”,也可以填“1+2(a+1)”;第2小题可以填“3+2(a-1)”,也可以填“1+2a”。这里,每一个数(含表示数的字母)、每一步算式的含义都要让学生结合题意弄清楚。不仅要明白每一题前后两式之间的联系与区别,而且要知道每一道算式所表达的规律,更要清楚两题中变量a的含义的变化。
第二,要引导学生综合各个情境的不同含义。例如,教学分数的意义。可以运用填空题“把( )平均分成( )份,表示这样的( )份”,来引导学生根据月饼图、长方形图、长度单位图、桃子图各自表示的分数,归纳出单位“1”及分数的含义。
第三,要引导学生推理同一道算式的不同含义。例如,教学长方形面积计算。在学生学完字母公式S=a×b进行综合练习时,可以引导他们推理出a×b= S,进而推出a×b=c,再根据“单价×数量=总价”进行类推,等等。让学生明白a×b=c可以表示两个数相乘的积,也可以表示长方形面积计算公式,还可以表示其他的数量关系式。
三、 把握关系,发展数学符号运算意识
数学符号运算意识主要是指主动地对含有字母的算式进行运算或推理,获得新结论,它包括能解释原式与化简结果。这里的算式,指简单的整式和简易方程。它的运算前提有二,一是掌握运算方法,二是明确对运算结果的要求。
在小学阶段,整式的化简主要集中在形如ax±bx,aπ±bπ之类,运用乘法分配律进行合并同类项;较复杂的简易方程主要有ax±bx=c, ax±b=c之类,运用等式的性质解方程。我们知道,通过有效的训练,学生能够掌握此类运算。问题主要有二:一是学生只是抽象地按规则进行运算,不去具象化思考,不去运用多种方法,不去寻找方法之间的关系;二是学生只是机械地解决此类问题,不去灵活思考结果之间的关系。换句话讲,我们要让学生把握好以上两种关系来全面发展数学符号运算意识。
1.注重方法之间的关系
就习题来讲,分析的角度和思路不同,就会形成不同的解题方法。如何呈现解题方法是教学的关键所在,让学生在解题的过程中提高运算能力是教学的重要举措。笔者认为,对于学生而言,解题方法的意义,不仅仅在于找到题目的答案,更在于发展他们的数学符号运算意识。也正因为后者,才有了对方法的发现进行教学的可能性,才有了对方法进行比较的价值,才有了对方法进行训练的必要性。
在解决一些代数问题时,绝大多数学生倾向于只是运用算术方法,或者只是运用代数方法,不去考虑同时运用它们,也不去分析解题方法之间存在的联系与区别。例如,做选择题:a+124=b+257,a与b相比,( )。①a>b;②a
2.注重结果之间的关系
运算结果往往是学生解题的唯一目标,对结果过于看重,也导致学生对其认可趋向偏执。尤其是对代数式进行运算,其结果不仅可以是一个数,而且可以是一道算式,学生往往难以接受,即使认同,也是囫囵吞枣。对运算结果的有效处理,不仅可以加深学生对运算符号及其运算本身的理解,还可以加深式与形、数与符号之间的理解,更可以通过结果之间关系的分析来发展学生数学符号运算意识。
第一,通过对算理的分析,加深对结果之间区别的认识。可以让学生在解决实际问题的过程中,通过提出问题、列式、说说算式每一步的意义等数学活动,来进一步明晰数学符号运算的规则,尤其是对结果的规定性。例如下面这道习题:利民公司运来a车蔬菜,每车装5吨,供应给菜场65吨。 ?学生能够根据条件提出如下问题:还剩多少吨蔬菜?列出如下算式:5a-65,5(a—65÷5)。通过讨论得出结果的两种形式:5(a—65÷5)=5a-65,5(a—65÷5)=5(a-13),它们分别使用了数量关系式“公司运来蔬菜的总吨数-供应给菜场的吨数=剩下的吨数”、“每车蔬菜的吨数×供应菜场后剩下的车数=剩下的吨数”,这就是它们主要的区别所在。
第二,通过部分与整体的对比,加深对结果之间联系的认识。可以让学生分析代数式不含字母的前几项的特征,找出算法,算出结果,再类推出整个代数式的结果。例如,计算1+2+4+8+…+m。可以先让学生计算1+2+4+8+16+32+64+128,找到算法“尾数×2-1”,再推出原代数式的结果2m-1,同时把结果255与“2m-1”进行比较。也可以在教学相关例题之后的综合练习中,把例题改编成含有字母的代数式,促进学生进行类推。比如,把例题++++改编成+++++…+,让学生由例题的结果1-推出改编题的结果1-。
综上,数学符号意识可以分成数学符号引入意识、理解意识和运算意识三种,其有效生成,需要立足需要,彰显变化,把握关系。
参考文献
[1] 教育部基础教育课程教材专家工作委员会编写.义务教育数学课程标准(2011年版)解读[M].北京:北京师范大学出版社,2012.
[2] 中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
【责任编辑:陈国庆】
