从数学本质出发 创设问题情境
2016-09-10徐丹阳
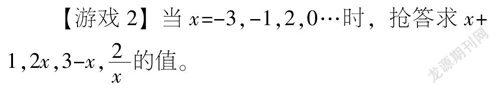

【摘 要】高效的课堂教学离不开有效的教学设计,而有效的教学设计的前提是把握教学内容的本质。分式与整式的本质区别在于给定字母值,代数式未必有值。把握好这一点,再引入概念、深化对概念的理解,进而掌握新知、巩固提高,简约高效的教学设计也就水到渠成了。
【关键词】分式;数学本质;教学设计
【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009(2016)03-0029-03
【作者简介】徐丹阳,浙江省温州市第二中学(浙江温州,325000)学科组长,浙江省特级教师,正高级教师;浙江省骨干高级访问学者、名师工作室指导师,浙江省教育厅课程分析教材编写成员,温州市首届名师,浙江师范大学、温州大学研究生导师。
分式与整式是两种不同的代数式,“分式”一课的有效教学需要做到三点:一是突显分式与整式的区别,突出分式的本质,让学生观察到分式的特征,得出分式的概念;二是以自然、简洁、明了的方式,让学生的思维经历从分数到分式的一次螺旋式上升,感受从具体到抽象、从特殊到一般的认识过程;三是让学生通过研究解决问题的过程,探究分式有意义的条件。为此,应当根据学生需要,通过设计目的性明确的简约有效的问题情境,达成教学目标。
一、概念引入
创设两个教学游戏,引出分式的概念。
【游戏1】①写一个代数式满足:当x=1时,代数式的值为2。②写一个代数式满足:当x=1时,代数式的值为2;并且,当x=2时,代数式的值为1。③写一个代数式满足:当x=1时,代数式的值为2;并且,当x=2时,代数式的值为1;当x=3时,代数式的值为。
对于①,许多学生会想到是2x或x+1。对于②,学生一般会思考一会儿,思维在整式范围内转悠,兴奋地得出3-x,也会有少量学生发现,此时就可以进入下一个游戏。如果没有出现分式,就继续第三个问题。
【游戏2】当x=-3,-1,2,0…时,抢答求x+1,2x,3-x,的值。
学生将x的值代入以上四个代数式求值,在兴奋抢答中,纷纷掉入圈套,大量出现当x=0时=0的错误。但很快会有“识货”的孩子“发现真理”而兴奋宣布:不对!分母是零!无意义!由此引入分式的概念:两个整式相除,并且除式中含有字母,像这样的代数式就叫分式。这类式子的特征是字母的某些取值使代数式无意义,原因在于分母含字母,取某值时,会出现值是零的情况。
【设计意图】综观当下的诸多教材,对于“分式”一课均采用取材于生活实际,即列举大量分式实例,通过列表达式的形式引入,体现数学来源于生活又服务于生活的特点,这种做法固然是合乎大多数教师的口味,但对于初一学生,却没有什么吸引力。而我上面的设计从培养函数意识的角度,让学生在初步感受对应关系中,亲自组建整式,并在整式不够用时,让分式自然地脱颖而出。更可贵的是,教师完全把发现的过程交由学生,让学生一起来思考,不同层次的学生都有不同层次的发挥,这对培养学生提出问题和解决问题的能力无疑起到了很好的作用。
与平常的列举大量分式实例引入分式相比,同样是获取不同代数式,但效果大不一样。一方面,这样简约的设计,符合学生的游戏挑战心理,不断升级的难度激起学生克服困难的极大热情,而每一次的成果又能促使其对下一轮挑战抱有更大的热情。而平常的列举式引入,是一种零散的平淡无奇的无目的的工作。另一方面,从结果上看,列举大量分式实例引入,尽管学生眼前是许多分式,但与学生已有经验并无关联。而本设计由字母与代数式数对的取值不同,引起代数式表达式的变化,让学生看到分式奇妙一角,紧接而来的代数式求值,让学生清晰地走进整式与分式的分水岭——存在一个x的值使得代数式无意义!打破原有的“给定字母值必有代数式值可求”的经验,这正是“分式与整式”本质的区别,也是最需要学生领悟的逻辑关系处。
笔者特别注重教学引入环节的教学设计,认为课堂教学的引入需要考虑下列三个方面:1.如何引导学生思考;2.思考什么内容;3.从何入手。本节课的教学将培养学生的函数意识作为教学的起点和核心点,设计求值游戏以学定教。唤起学生由直觉思维走向自觉思考,简约不简单。学生思维从无序到有序的发展过程,是享受数学美的过程,通过深入思考,唤起了学生自觉提出问题的积极性,从而进入“為什么代数式无意义”的探讨。我们知道研究问题比解决问题更重要,以上精心设计的“引入环节”,所激发的学习兴趣和探究欲望,在相当程度上决定了整节课分式的学习效益和效率。
二、概念理解
加深学生对分式概念的理解,要从两个方面进行。一是设计探究活动让学生类比分数和分式,进而体会分式的意义;二是让学生将分式纳入已有的多项式、单项式、整式、代数式等知识结构中。
探究活动1:已知老师原地起跳,3秒钟跳的高度为46厘米,t秒钟跳的高度为59厘米,5秒钟跳的高度为h厘米,①求老师跳高的平均速度;②若t=4,h=75,那么老师跳了m秒,会跳多高呢?
根据上述条件,对于问题①,学生会很自然地列出代数式;;,此时不应当满足于此,而应让学生辨别哪些是分式,以此巩固分式的概念。对于问题②,学生会发现每个分数都近似于15,即老师的平均速度约为15厘米每秒,m秒跳的高度是15m厘米。所以,老师的平均速度可以表示为分式:。这里要提醒学生一个重要的结论:分式比分数更具有一般性。
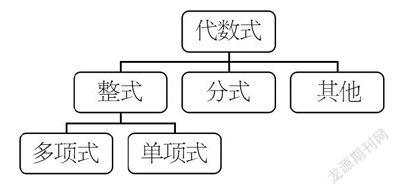
探究活动2:合作讨论多项式、单项式、整式、代数式和分式的结构关系。引导学生画出如下的关系图。
【设计意图】由于分式是分数的代数化,所以其性质与运算是完全类似的。因此,我们的设计十分注重观察、归纳、类比、猜想等思维方法的应用。如:在分式的探索过程中,采用了观察、类比的方法,通过观察、猜想让学生在讨论、交流中获得分式的概念,分式表达式也是通过抽象、概括获得的。这样,既渗透了常用的数学思维方法,又培养了学生的数学合理推理能力;更重要的是学生在获得这些知识时,形成了自主探索、合作交流的学习习惯,这是非常重要的。
经历本环节后,学生能感受分式与分数的联系与区别,清楚分式源于分数,又比分数更具有一般性。紧接着的任务是体会分式的模型思想,进一步掌握分式成立的条件。
三、掌握新知
上面的教学过程中已经突出了分式的特点,下面设计5道例题来研究分式成立的条件。
例1:下列的式子中哪些是整式,哪些是分式?
例2:请在括号内添加一个代数式,使得原式成为分式。
例3:成立有条件吗?
例4:对于分式,(1)当x取什么值时,分式有意义?(2)当x取什么值时,分式的值为零?
例5:巩固练习(1)当x 时,分式有意义;
(2)当x 时,分式有意义;
(3)当b 时,分式有意义;
(4)当x 时,分式有意义;
(5)当x、y满足关系 时,分式有意义;
(6)当x= 时,分式的值等于0。
特别声明:在本文中,若没有特别说明,分式的字母取值都不使分母为零。
【设计意图】例1目的是初步让学生学会从形式上判断分式。例2则紧抓分式的分子与分母的共性与异性,回归概念,揭示分式的本质属性。例3是对上面两个例题的解后反思与总结。例4强调当分子等于0且分母不等于0時分式的值为0。例5通过变换问题的背景,培养学生的应变能力。
四、巩固提高
至此,分式的基本知识就教学完毕了,下面需要设计例题巩固知识。对于例题的设计可以开放条件和结论让学生进行仿写。例如:对于分式,可设计的问题有:①当x取不同值时,对应分式的值是多少?②当x为何值时,分式的值是1?仿照于此,可以让学生就分式提出问题。
分式最终是表示具体情境中数量的模型,为了体现这一点,还应当设计应用题通过实际问题来巩固分式意义。
例如,甲乙两人从一条公路的某处出发,同向而行,已知甲每小时行a千米,乙每小时行b千米(a>b)。如果乙提前1小时出发,那么甲追上乙需要多少时间?若取a=b,此时表示的实际意义是什么?
【设计意图】以上练习巩固针对性强,通过仿写来开放条件和结论,不仅可以加深学生对基础知识的理解,使学生熟练地掌握解决这一类问题的方法,为运用分式概念提供范例,其解法体现了解决这一类问题的通性通法,蕴含了解决问题的基本数学思想和方法,能做到高效练习。
本课教学通过培养学生的函数意识,凸显教学的最本质内容,有意识地引导学生从“变”的现象中发现“不变”的本质,从分式与整式的本质区别中突围。在给出分式的概念时,通过观察、归纳,抓住分式的实质,总结出整式与分式的异同,通过设计含有矛盾冲突的问题,突出数学问题的本质,得出分式的概念,讲清楚学生观察到的分式特征;在知识归纳与方法提升方面,旨在养成有效的思维习惯,不断实践,给所有学生以表达的机会,学会总结提炼,这些都是本课的亮点。
在教学过程中,教师的主要作用是组织学生开展有效的探索,其目的是让学生自然地、自觉地把分式新知纳入到原来的知识体系中,完善认知结构。活动的目的是让学生通过经历探究、思考、抽象、预测、推理、反思等过程,逐步达到对分式概念的意会、感悟,并能积累解决和分析问题的基本经验,将这些经验迁移运用到后续的数学学习中去。
学生在这样的学习过程中,不断发现问题、提出问题,进而不断解决问题。学生的学习实现了主动高效。在以上问题情境的创设中,类比的思想被广泛应用,学生不断地用类比思想去探索新知,在学习分式时,用分数来类比,这个类比的过程并不是简单地照搬照抄的过程,而是一个让学生感悟的过程,是从相似点中“悟”到不同点。
总之,唯有深度解读分式概念,教师摆脱以课堂讲授新知为主、学生被动听讲的局面,用较大的精力投入教材解读,让课堂中有愉悦高效的学习情境,满足学生对数学课堂的需求,方能达到简约高效的课堂教学的目标。
