《函数y=Asin（ωx+φ）的图象》学习工具应用综述

吕艳香

● 特色与亮点

在本节课的教学中，学习工具的使用点有展示现实情境，画出函数图象，对参数Α，ω，φ赋值并进行动态跟踪，对函数图象、函数解析式进行动态关联，拓展应用范围，为学生提供更大的创新思维空间。学习工具的应用化解了函数的高度抽象性带来的学习困惑，使教学内容可视化、动态化、可操作，增强了学生学习活动的探索性。

● 使用背景

我校学生的整体水平在北京市朝阳区处于中等水平，学生数学基础比较薄弱，基本数学素养相对较低，但学生思维比较活跃，学习积极性较高。在本节课之前学生已经学习了正弦函数y=sinx的图象、性质及五点法画简图，并且有了一定的识图能力。但是学生对我ω、φ两个参数对图象带来的影响在理解上有一定的难度。因此我利用了这一学习工具，旨在让学生通过动手实践，在操作过程中更好地观察和发现对应变化点的坐标之间的联系，从而真正理解变换的实质。

● 设计思路及内容结构

为学生提供一人一台TI图形计算器的学习环境，要求学生利用信息技术快捷地作图象。学生通过调节参数赋值、拖动等自主操作，观察相应图象的变化，调动多种感官，动静结合、手脑并用地直观感知参数Α，ω，φ（ω>0，A>0）的变化对函数y=Asin（ωx+φ）图象的影响。

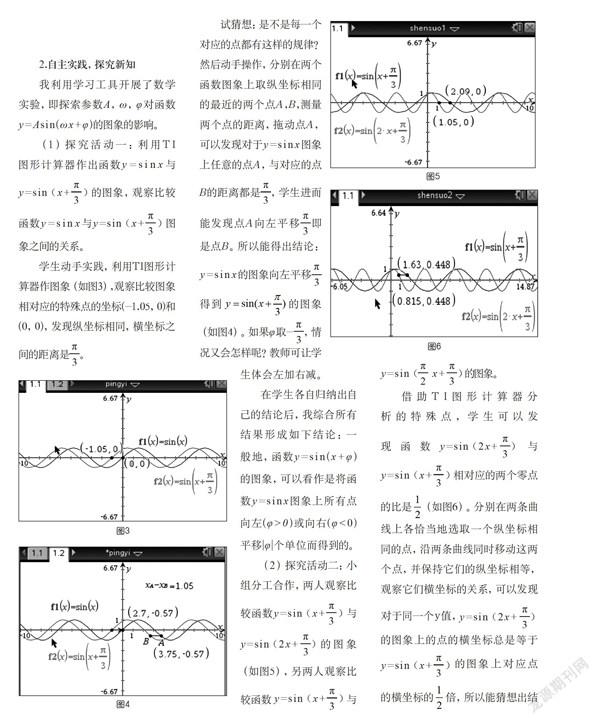
本课的教学过程分为五个环节完成，本文着重介绍学习工具利用率较高的前三个环节。

1.创设情境，引入新课

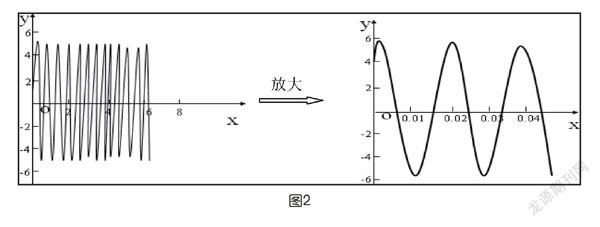
打开学习工具，我首先展示了如图1的一个弹簧振动模拟实验图。随后出示图2，它是交流电的电流y随时间x变化的图象。

我们看到不同的例子中函数的图象有所不同，那么是什么原因使得函数的图象不同呢？我们应该如何探究参数Α，ω，φ（ω>0，A>0）对函数y=Asin（ωx+φ）图象的影响呢？对于较多因素影响的问题我引导学生采用先“各个击破”再“归纳整合”的策略，化繁为简，化难为易。

● 评价与反思

在课堂教学中，学生能利用TI图形计算器快捷地作出函数图象，化解了手工作图带来的费时且不准确的困难。借助信息技术让参数“动起来”，实现了“参数变化对函数图象影响”的可视化，弥补了传统教学在直观感、立体感、动态感方面的不足，很容易化解了教学难点，让学生更系统直观地感受到各种参数对函数图象的影响。信息技术的运用激发了学生的学习兴趣，实现了高效课堂。

在教学中，教师应该给学生足够的时间和空间，让学生在自主学习与合作探究中主动建构新知识。

● 幕前幕后

NOC活动，是面向广大师生开展的，运用信息技术，培养创新思维、提升实践能力、增强知识产权意识的一项活动。这对中小学普及信息技术教育，全面推进素质教育，实现高效课堂具有积极的意义。在此特别感谢组委会给我们教师提供了这样的展示、观摩和交流的平台，更感谢各位专家和评委的点评。回顾参赛前后，从一开始通知参加NOC活动全国决赛，对作品的酝酿，再到专家点评后获得的启发和这一年来的教学实践，让我真正地体会到数字化学习工具的作用在于能构建积极互动的教育新模式。学生在动手实践、合作学习、自主学习和探究活动中，借助工具实现内容的可视化、动态化、可操作，增强学习活动的探索性，发挥学生思维的创造性，促进他们对重难点知识的理解，实现了有效教学。

点评

吕老师的《函数y=Asin（ωx+φ）的图象》的教学运用了TI图形计算器，学习工具介入的数学课程使得教学方式发生了巨大的变化，正如课程标准指出的“现代信息技术的广泛应用正在对数学课程内容、数学教学、数学学习等方面产生深刻的影响”。在教学中，如何将信息技术与数学课程内容有机整合是数学整合课程需要研究的重要课题，无论整合的形式如何变化，整合的原则都应该是有利于学生对数学本质的认识，本节课在信息技术与数学课程内容的整合方面有如下特点：

第一，整合应利用技术来呈现以往课堂教学中难以快速呈现的课程内容。在本节课中，如果没有学习工具，一个学生只能徒手画几个函数图象，而使用学习工具则可以根据实际探索的需要画几个、十几个甚至几十个函数的图象。在学习工具的支持下师生可以从繁琐和重复的画图中解脱出来，集中精力对众多图象进行观察、分析，从诸图象的变化中归纳出隐藏的内在联系，把握变换的本质规律。

第二，学习工具的介入使得学生的探索更适于个性化认知，在探究函数y=Asin（ωx+φ）与y=sinx的图象间的变换关系时，不同的学生可以利用手中的TI图形计算器按照自己的想法A，ω，φ赋不同的值。例如，某学生对ω对函数图象的影响理解不到位，则他（她）可以在教师要求的基础上对ω再赋不同的值进行观察分析，显然这样的探究活动更有利于学生对知识的理解与落实。

第三，学习工具介入数学课堂不仅是一种新的学习方式，更体现了新的教学理念。从社会发展的角度看，学生在学校所学的知识只是学生未来一生中所需知识的一小部分，因此基础教育不仅要教会学生知识，更要使学生学会学习，特别是在信息社会中要学会使用学习工具来学习，学生在学习工具支持下的数学探究学习，就是以学生发展为目标的数学探究学习，这样的学习方式会使学生受益终身，实现可持续发展。

鉴于此，我给予以下三个建议：①本节课教师已经对A，ω，φ赋值的顺序做出安排，但对某些能力较强的学生，其实不必强求。②TI图形计算器具有局域网的联网功能，教师如果恰当使用这一功能，会更容易把握教学过程的预设与生成，教师可以利用网络把每位学生的探究过程微缩图都实时地呈现在大屏幕上，并可据此把握全体学生的正确率、进度等。另外对学生学习中的典型问题，教师可以根据需求及时进行进一步的启发或根据情况调整预设，总之在TI图形计算器与局域网的学习环境中，学习进程中的预设与生成的矛盾都呈现可视化的特点，这使得教师更容易把握解决矛盾的方法，提高教学效率。

（点评人：北京市朝阳区教育研究中心 袁京生）