严格对角占优M-矩阵的逆矩阵的无穷大范数的上界估计
2016-09-09赵仁庆
赵仁庆
(楚雄师范学院数学与统计学院,云南楚雄675000)
严格对角占优M-矩阵的逆矩阵的无穷大范数的上界估计
赵仁庆
(楚雄师范学院数学与统计学院,云南楚雄675000)
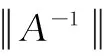
对角占优矩阵;M-矩阵;无穷大范数;最小特征值
引言
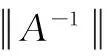
1 预备知识
为叙述方便,给出本文需要用到的一些记号。用Cn×n(Rn×n)表示n×n阶复(实)矩阵的集合,记
N={1,2,…n},m≤i,j,k≤n
设A=(aij)∈Rn×n且aii≠0,
ln=un=0

定义2[3]设A=(aij)∈Rn×n,如果aij≥0,对任意i,j∈N,即A的所有元素是非负的,则称A为非负矩阵,记为A≥0。
定义3[3]设A为Z-矩阵,A可逆且A-1≥0,则称A为非奇异M-矩阵。
定义4[4]设A=(aij)∈Rn×n,如果满足条件

(2)(2)J(A)≠Φ;
(3)对于任意i∈N,i∉J(A),存在i1,i2,...,ik使aii1ai1i2…aik-1ik≠0,ik∈J(A);
则称A为弱链对角占优矩阵。
定义5[4]设A=(aij)∈Rn×n,若J(A)=N,则称A为行严格对角占优矩阵。
注由定义4和定义5知,若A为严格对角占优矩阵,则A为弱链对角占优矩阵。
引理1[4]设A=(aij)∈Rn×n是弱链对角占优M-矩阵,则A(k,n)(k = 1, … ,n-1)也是弱链对角占优的M-矩阵。这里A(n1,n2)表示由A=(aij)∈Rn×n的n1至n2行和n1至n2列的元素组成的子矩阵。例如A(2,n)表示由A=(aij)∈Rn×n的2至n行和2至n列的元素组成的子矩阵。

其中

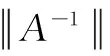
定理1[1]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则
(1)
定理2[2]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则
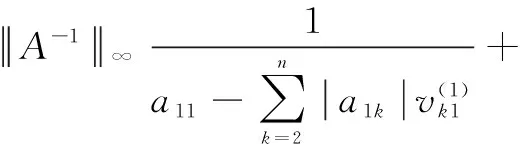
(2)
引理4[5]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则A-1=(αij)满足
(3)
特别当i=1时,有
(4)
引理5设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则A-1=(αij)满足
(5)
证明由引理4得
αii(aii-aiidiω(m))
故

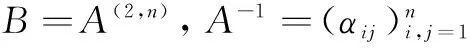
(6)
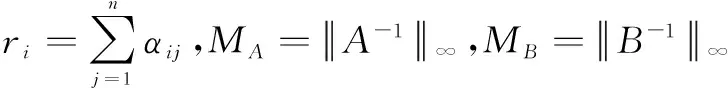
当2≤i≤n时,由引理2和(4)式得
故对2≤i≤n,由引理2知
r1ω(1)+MB
若r1≤ω(1)r1+MB,则
若r1>ω(1)r1+MB,则
因此,有
定理得证。
结合引理1,对定理3利用迭代法得如下结论。
定理4设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则
算法综合比较了NLMS和FDNLMS算法的性能,比较指标包括处理时间以及自适应滤波器失调系数和回声返回损耗增益值:
(7)
由引理3和定理4得如下推论。
推论1设A=(aij)∈Rn×n是严格对角占优M-矩阵,则A的最小
q(A)>
(8)
定理5设A=(aij)∈Rn×n是严格对角占优M-矩阵,则
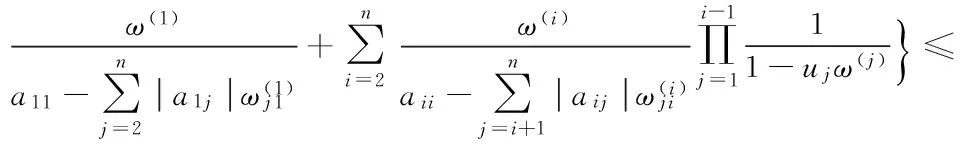
(9)
且
故结论成立。
注由定理5可知,本文的结论在一定条件下改进了文献[2]中的结果。
例1设

用matlab7.0计算得
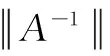

[2] 李艳艳,李耀堂.严格对角占优M-矩阵的逆矩阵的无穷大范数上界的估计[J].云南民族大学学报:自然科学版,2012,21(1):52-56.
[3] 陈公宁.矩阵理论与应用[M].北京:科学出版社,2007.
[4] SHIVAKUMAR P N,WILLIAMS J J,YE Q,et al.On two-sided bounds related to weakly diagonally dominant M-matrces with application to digita dynamics[J].Matrix Anal.Appl,1996,17(2):298-312.
[5] 王峰.非奇异M-矩阵的逆矩阵和M-矩阵的Hadamard积的最小特征值下界估计[J].应用数学,2013,26(2):341-345.
[7] 赵仁庆,熊昌明,李耀堂.块H-矩阵的判定及其逆底无穷大范数的上界[J].云南大学学报:自然科学版,2011,33(2):125-130.
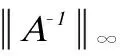
[9] 王永.严格对角占优M-矩阵的逆矩阵的无穷大范数上界的估计的新上界[J].工程数学报,2015(5):719-725.
[10] 赵仁庆,刘鹏.弱链对角占优M-矩阵的逆矩阵的无穷大范数的上界估计[J].楚雄师范学院学报,2014,29(3):5-10.
[11] 赵云平,李朝迁.广义M-矩阵的逆矩阵范数的估计[J].贵州大学学报:自然科学版,2014,31(4):8-10.
[12] WEN Li.The intinity norm bound for the inverse of nonsingular diagonal dominant matrices[J].Appl.Math.Lett.,2008,21:258-263.
[13] LI Y T,CHEN F B,WANG D F.New lower bounds on eigenvalue of the Hadamard product of an M-matrix and its inverses[J].Linear Algebra Appl,2009,430:1423-1431.
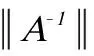
[15] 赵仁庆,钟振华,刘鹏.GS-SDD矩阵的逆矩阵的无穷范数和最小奇异值的估计[J].楚雄师范学院学报,2014,29(6):1-5.
Estimation on Upper Bounds of the Infinity Norms of Inverses for Strictly Diagonally Dominant M-matrices
ZHAO Renqing
(School of Mathematics and Statistics, Chuxiong Normal University, Chuxiong 675000, China)

diagonal dominance matrix; M-matrix; infinity norms; smallest eigenvalue
2016-01-21
楚雄师范学院项目(12YJRC10)
赵仁庆(1985-),女,云南腾冲人,讲师,硕士,主要从事矩阵理论及其应用方面的研究,(E-mail)422652443@qq.com
1673-1549(2016)02-0075-05
10.11863/j.suse.2016.02.15
O151.21
A
