基于Richards方程的不同氮肥处理的旱地小麦茎秆生长的动态模拟

逯玉兰，燕振刚，李 广,王联国，董莉霞，王 钧

(1.甘肃农业大学 信息科学技术学院，甘肃 兰州 730070；2.甘肃农业大学 林学院，甘肃 兰州 730070；3.甘肃省干旱生境作物学重点实验室，甘肃 兰州 730070)



基于Richards方程的不同氮肥处理的旱地小麦茎秆生长的动态模拟

逯玉兰1，燕振刚1，李 广2,3,王联国1，董莉霞1，王 钧1

(1.甘肃农业大学 信息科学技术学院，甘肃 兰州 730070；2.甘肃农业大学 林学院，甘肃 兰州 730070；3.甘肃省干旱生境作物学重点实验室，甘肃 兰州 730070)

以实测试验数据为基础，分析旱地小麦茎秆生长的动态变化，用Richards方程描述茎秆的节间长度和粗度的动态变化过程，并以不同氮肥处理的旱地小麦对模型进行了检验。针对Richards方程参数多且参数估计复杂的问题，用粒子群优化算法进行Richards方程参数估计，将经验性和机理性有机结合。检验结果表明：茎秆的节间长度和粗度测量值与模拟值表现了很好的一致性，长度的RMSE范围为0.124～0.932，粗度的RMSE范围为0.012～0.076，模型具有很好的适用性和预测性。

Richards方程；氮肥处理；旱地小麦；茎秆生长；粒子群优化算法

0　引言

作物地上部器官的形态建成模型是作物生长模型中的重要部分，掌握作物的地上部器官形态变化规律，定量描述作物形态建成过程，对作物品质和产量的形成具有重要的实际应用价值。同时，也是虚拟作物和作物可视化研究的关键。典型的地上部器官的形态建成模型有Mitscherhch、Compertz、Brody和Logistic等。由于它们具有固定的拐点，只能描述生物生长的一种特定形状的S曲线，或者说完整S曲线的一个特定部分[1]。Richards方程能够模拟生物生长的各个阶段，具有更广泛的实用性。徐寿军等[2]运用Richards方程建立了大豆茎秆、叶片和豆荚生长的动态模型。李红岭等[3]以生理发育时间为步长，用Richards方程模拟了甘肃大麦茎秆节间伸长和节间增粗的动态过程。但Richards方程含有的参数多，参数估计较复杂[4]。本文采用粒子群优化算法进行Richards方程的参数估计，进而构建旱地小麦茎秆伸长和增粗的动态模型。

1　材料与方法

1.1试验处理

本试验于2013～2015年在甘肃农业大学农业生态工程研究所开展，供试品种为黄土丘陵沟壑地区种植的有代表性的小麦品种定西35号和西旱2号。土壤质地为砂土，地力中等，有机质含量约为0.92 g/kg、速效氮42.47 mg/kg、速效钾75.2 mg/kg、速效磷15.64 mg/kg[5-8]。试验设N1、N2、N33个氮肥处理，施氮量分别为100、175、250 kg/hm2。氮肥分两次施入，基肥和追肥的比例为7∶3，基肥在播种前施入，追肥在拔节期施入。磷、钾肥作为基肥一次性施足，P2O5用量300 kg/hm2，KCl用量105 kg/hm2。试验为裂区设计[9]，氮肥处理为主区，品种为副区，2次重复，每个小区面积16 m2，3月15日播种，栽培管理措施同大田管理。

1.2茎秆长度和粗度的测算方法

每处理随机选取10株长势相同的小麦挂牌标记，从拔节期到灌浆期每1 d测量1次主茎的节间长度和粗度，所测10株的节间长度平均值节间粗度平均值为该处理该次的测算值。节间长度用皮尺测量，节间粗度用游标卡尺测量，测量节间的最粗处即为节间粗度。

1.3模型建立与模型检验方法

应用试验数据建立节间长度和粗度模拟模型。模型检验方法采用国际上通用的均方根误差(RMSE)。

均方根误差(RMSE)值越小，说明测量值与模拟值的一致性越好，从而它们之间的偏差越小，即模型越可靠，模拟结果越准确[10]。因此，RMSE能够反映模型的预测性，其计算公式为：

(1)

公式(1)中，OBSi为实测值；SIMi为模拟值；n为样本容量；i为样本序号。

2　模型的建立

2.1节间伸长的模拟模型

小麦节间的伸长经历从慢到快再到慢的过程，本研究所选旱地小麦品种地上茎节为6节，节间伸长开始于拔节期，结束于灌浆期。基部第1节先开始伸长，其余各节从上而下依次伸长，各节间开始伸长的时间间隔为2.2个生理日。各节间伸长的模拟模型为：

n=1,2,3,4,5,6

(2)

公式(2)中，PDT为生理发育时间[11]，其中7.2为小麦第1节间开始伸长的生理发育时间；INL(PDT)n为小麦在某一生理发育时刻第n节的节间长度；INLmaxn为小麦第n节间长度的最大值，如表1所示。m、kn、bn是模型参数，用粒子群优化算法确定，用粒子群优化算法确定Richards方程的模型参数详见文献[12]。

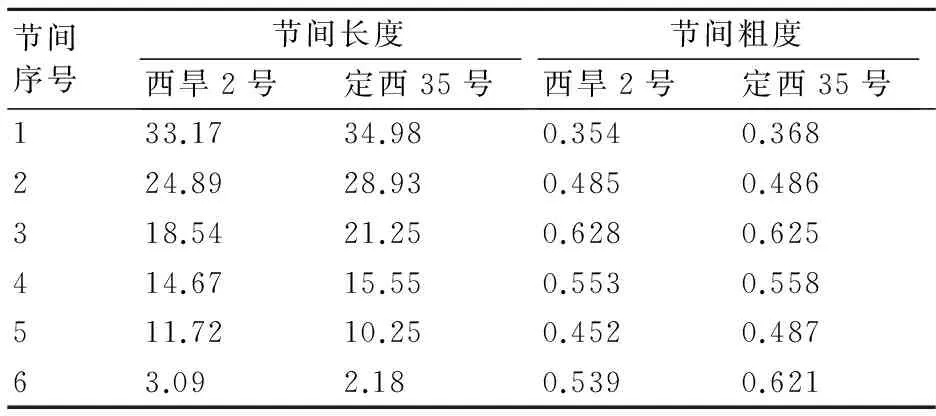
表1　旱地小麦节间长度和粗度的最大值 cm

注:节间序号1为穗下第1节间，以此类推。

在基于粒子群优化算法的Richards参数估计实验中，使用Matlab 2012b作为编写粒子群算法的工具，并使算法中的迭代次数达到10000次。程序代码分为两块，一是粒子群算法pso.m，二是适应度函数fitness.m。西旱2号第1节间长度的拟合曲线如图1所示；最优值变化曲线如图2所示。拟合曲线表明，实测值基本在拟合的Richards曲线上，说明拟合效果良好。

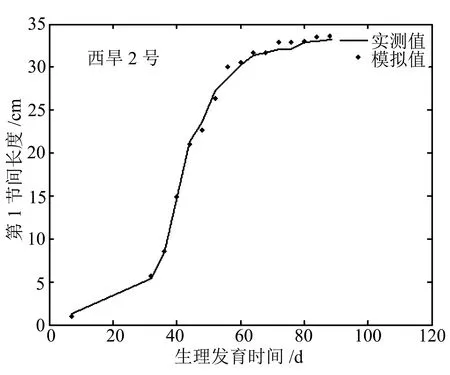
图1　节间长度拟合曲线

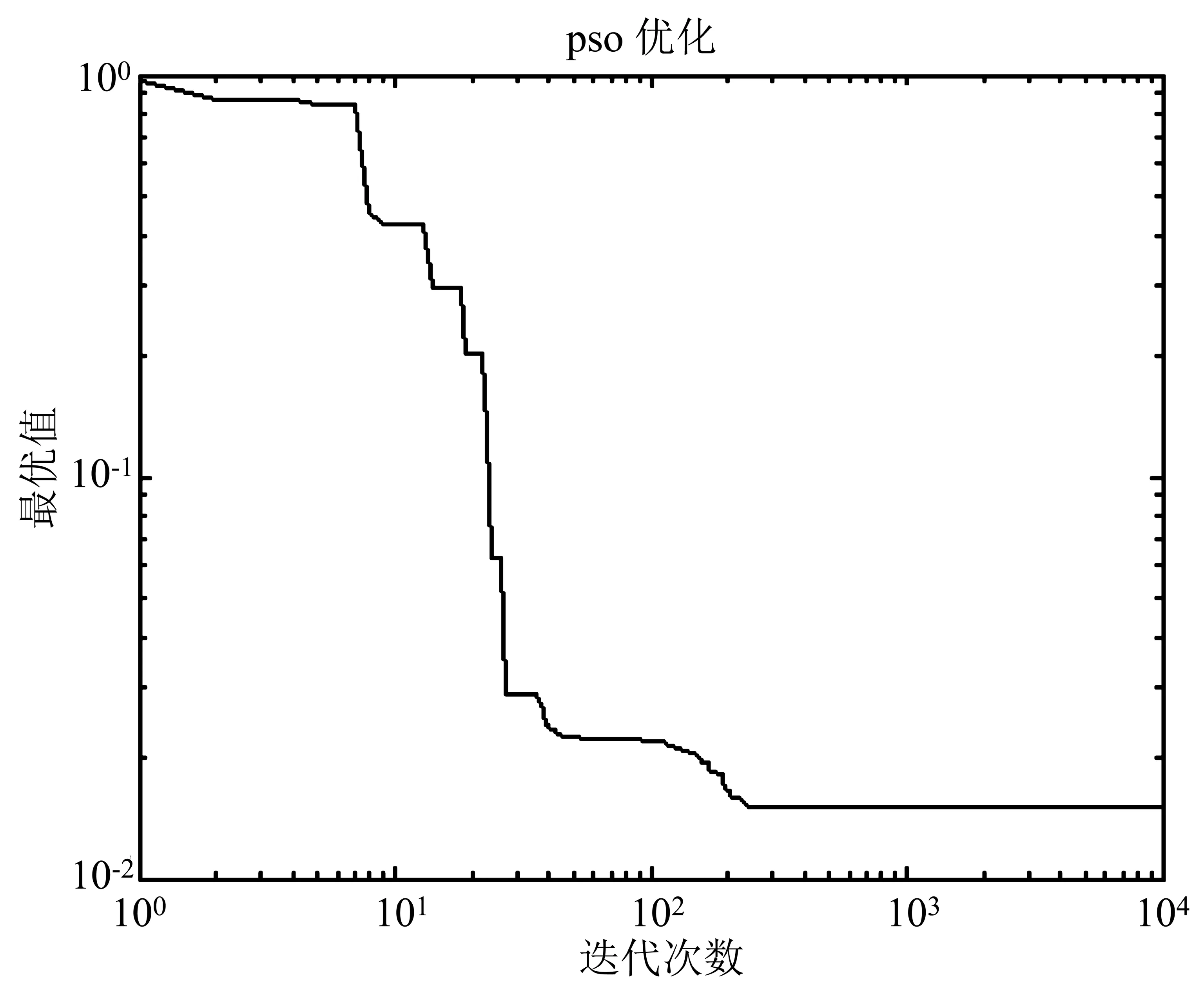
图2　最优值变化曲线

NDF为氮素影响因子，其计算公式[13]为：

(3)

公式(3)中，TANCpol为小麦地上部植株实际含氮量，TCNPpol为临界含氮量，TMNCpol为最小含氮量。相关资料表明，小麦地上部植株最小含氮量和临界含氮量均与生理发育时间呈函数关系，如图3所示。

2.2节间增粗的模拟模型

本研究试验结果表明，小麦节间的增粗跟伸长类似，也是经历从慢到快再到慢的过程。与节间长度不同的是，小麦各节间粗度先增加后减少，最大值出现在第3节，各节间增粗的模拟模型同公式(2)。

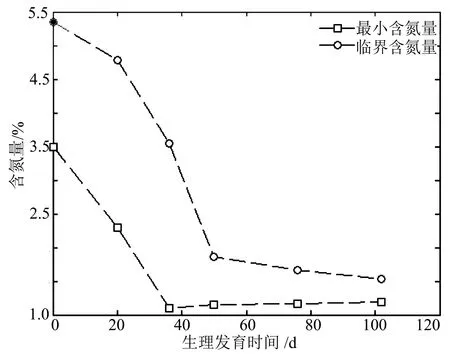
图3　旱地小麦地上部植株临界和最小含氮量随生理发育时间的动态变化

3　模型的检验

分别选取不同品种不同氮肥处理的具有代表性的旱地小麦3个生长阶段的5个观测日数据对模型进行检验，结果见表2。

从表2可以看出，不同品种和氮肥处理茎秆长度的RMSE范围为0.124～0.932；茎秆粗度的RMSE范围为0.012～0.076。检验结果表明，本模型对不同品种和氮肥处理条件下旱地小麦的茎秆长度和粗度有很好的预测性。

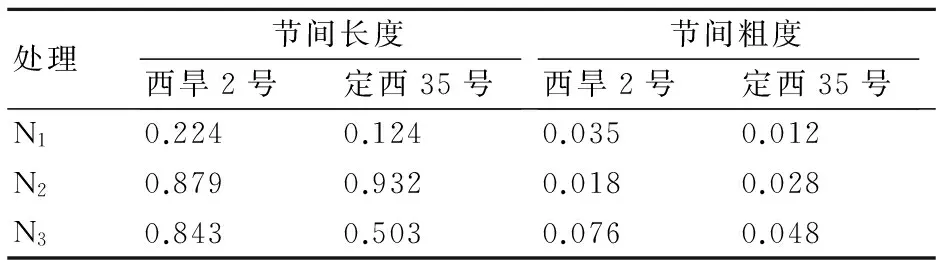
表2　不同品种和氮肥处理水表茎秆长度和粗度RMSE值 cm

4　小结与讨论

本文用茎秆节间长度和粗度最大值作为品种遗传参数，考虑了氮素对茎秆生长的影响，以实测试验数据为基础，用Richards方程描述节间长度和粗度的

动态变化过程。针对Richards方程参数多且参数估计复杂的问题，本文用粒子群优化算法进行Richards方程参数估计，将经验性和机理性有机结合，检验结果表明模型是可行的。茎秆的节间长度和粗度测量值与模拟值表现了很好的一致性，长度的RMSE范围为0.124～0.932，粗度的RMSE范围为0.012～0.076。

由于资料的限制，本文仅对该模型进行了测试和验证，今后要在田间试验的基础上进一步评价和完善模型的适用性和预测性，为虚拟作物系统的开发提供理论依据。

[1] 邢黎峰,孙明高,王元军.生物生长的Richards模型[J].生物数学学报,1998,13(3):348-349.

[2] 徐寿军,李志刚,杨恒山,等.大豆茎秆、叶片及豆荚生长的动态模拟[J].农业工程学报,2013,29(20):151-159.

[3] 李红岭,高晓阳,张明艳,等.大麦茎秆生长动态模拟模型[J].干旱地区农业研究,2012(4):129-132.

[4] 程毛林.Richards模型参数估计及其模型应用[J].数学的实践与认识,2010,40(12):139-140.

[5] 李广,黄高宝.基于APSIM模型的降水量分配对旱地小麦和豌豆产量影响的研究[J].中国生态农业学报,2010,18(2):342-347.

[6] 李广,黄高宝,王琦,等.基于APSIM模型的旱地小麦和豌豆水肥协同效应分析[J].草业学报,2011,20(5):151-159.

[7] 李广,黄高宝,William B,等.APSIM模型在黄土丘陵沟壑区不同耕作措施中的适用性[J].生态学报,2009,29(5)：2655-2663.

[8] 李广,李玥,黄高宝,等.基于APSIM模型旱地春小麦产量对温度和CO2浓度升高的响应[J].中国生态农业学报,2012,20(8):1088-1095.

[9] 白青海,徐寿军,董永义,等.大麦叶面积指数的模拟研究[J].生物数学学报,2009,24(2):321-328.

[10] 黄占斌,山仑.水分利用效率及其生理生态机理研究进展[J].生态农业研究,1998,6(4):19-23.

[11] 徐寿军,顾小莉,庄恒扬,等.大麦顶端发育和物候期的模拟[J].麦类作物学报,2006,26(3):123-127.

[12] 燕振刚,胡贺年,李广.基于粒子群优化算法的Richards模型参数估计和算法有效性[J].计算机应用,2014,34(10):2827-2830.

[13] Zhao C J，Wang J H，Wu H R，et al. Simulation models and deduction system for interspace description of wheat leaf shape [J]. Trans CSAE, 2002, 18(5): 221-225.

(责任编辑：许晶晶)

Dynamic Simulation of Stem Growth of Dryland Wheat Treated with Nitrogen Fertilizer Based on Richards Equation

LU Yu-lan1, YAN Zhen-gang1, LI Guang2,3, WANG Lian-guo1, DONG Li-xia1, WANG Jun1

(1. College of Information Science and Technology, Gansu Agricultural University, Lanzhou 730070, China;2. College of Forestry, Gansu Agricultural University, Lanzhou 730070, China;3. Gansu Provincial Key Laboratory of Aridland Crop Science, Lanzhou 730070, China)

Based on the experimental data, this paper analyzed the dynamic changes in stem growth of dryland wheat, described the dynamic change process of stem internode length and thickness by using Richards equation, and examined the model through dryland wheat which was treated with different nitrogen fertilizers. Aiming at the problems of more parameters and complex parameter estimation of Richards equation, we used the particle swarm optimization algorithm to estimate the parameters of Richards equation, which could combine the experience with the mechanism. The statistical analysis of the model examination showed that: there was a good consistency between the measured value and simulated value of stem internode length and thickness; the RMSE of internode length was between 0.124 and 0.932, and the RMSE of internode thickness was 0.012～0.076. Therefore, the model had very good applicability and predictability.

Richards equation; Nitrogen fertilizer treatment; Dryland wheat; Stem growth; Particle swarm optimization

2016-02-14

甘肃省自然科学基金(1308RJZA215)；甘肃农业大学盛彤笙创新基金(GSAU-STS-1231)；甘肃省自然科学基金(1308RJZA272)；甘肃省科技支撑计划(144NKCA038)；甘肃省高等学校基本科研业务费项目；国家自然科学基金(31060178)；干旱生境作物学重点实验室开放基金(GSCS-2010 -11)。

逯玉兰(1986─)，女，甘肃天祝人，讲师,硕士，研究方向:农业信息技术。

S512.1

A

1001-8581(2016)08-0010-03