互补储能系统的优化建模与控制策略

王　波

(国网安徽省电力公司检修公司，合肥　230061)



互补储能系统的优化建模与控制策略

王波

(国网安徽省电力公司检修公司，合肥230061)

针对单一蓄电池储能系统功率密度低和超级电容储能系统能量密度低的问题，结合二者的特性，提出一种互补储能控制策略，从而充分发挥它们的优势。最后通过数学建模和仿真，结果表明互补储能系统在抑制可再生能源发电系统功率波动上具有明显的优势。

蓄电池；超级电容；建模；控制策略

风力发电、光伏发电系统受天气变化影响比较大，其输出功率呈现不同程度的波动性、随机性和间歇性，而电网对于接入系统中的可再生能源发电功率往往提出了非常严格的要求，例如限制其功率变化率、注入确定的功率等。因此，需要引入储能系统对可再生能源输出功率波动进行平抑，以满足系统给定的目标要求。

蓄电池储能系统具有能量密度高、功率密度小的特点，适合平抑长期平稳的小功率波动，但是在大功率波动时会出现难以响应的问题。超级电容器功率密度高但是其能量密度较低，在长时间的工作下可能会存在能量的不足，适合平抑具有短期间歇性的尖峰功率波动[1-4]。根据它们两者之间在功率和能量上的互补性特点，本文研究了蓄电池-超级电容互补储能系统及其控制策略，充分发挥二者各自的优势，克服单一储能系统存在的缺陷。

1　互补储能系统的数学建模

由于本文考虑的是数学模型，不考虑超级电容器和蓄电池的电路模型及其内部工作过程，并且在数学模型上超级电容和蓄电池储能系统是相似的[5-7]，因此可从剩余电量递推关系、充放电深度和功率约束几个角度考虑对它们进行数学建模。

1.1储能系统的剩余电量计算

剩余电量即荷电状态是储能系统充放电能力的重要标志，它在充放电过程中不断地发生变化，其变化量与该时间段内充放电功率、自放电率以及充放电效率有关，通过测量超级电容和蓄电池端电压可以估计其荷电状态[8]。其电量的递推关系如下：

(1)

(2)

式中SOCES(t)——第t个时段结束时储能系统的剩余电量；SOCES(t-1)——第t-1个时段结束时剩余电量；δES表示储能系统自放电率，%/min；PES——储能系统充、放电功率大小，MW，大于0表示放电，反之表示充电；ηES,c和ηES,d——储能系统充、放电效率的大小，%，通常超级电容的充放电效率高达95%，蓄电池的充放电效率在80%～90%；EES储能系统的额定容量，MWh。

1.2充放电深度限制

为了保证蓄电池和超级电容的持续正常工作，需要根据它们的充放电深度进行剩余电量的限制：

SOCES，max≤SOCES(t)≤SOCES，max

(3)

SOCES，min=1-DODESSOCES，max=DOCES

(4)

式中SOCES,min，SOCES,max——储能系统剩余电量约束下限和上限；DOCES，DODES——储能系统的限定充电深度和放电深度，蓄电池一般取DODB=0.8，DOCB=0.85，超级电容DODSC=0.85，DOCSC=0.95。同时为了保证开始就能够充放电，通常可取剩余电量初值SOCES(0)=(0.0.6)EC。

1.3最大脉冲充放电功率约束

储能系统的最大充放电功率允许值由当前剩余电量和最大脉冲充放电持续功率决定

(1)充电过程

Pc，mac(t)=

(5)

(2)放电过程

(6)

式中Pc,max(t)，Pd,max(t)——第t个时段储能系统的最大充、放电功率允许值，MW；PmaxC，PmaxD——储能系统最大脉冲充、放电持续功率，MW。

对于新型储能电池可取：

PmaxC，B=Pn，B，PmaxD，B=Nmax，BDPn，B

PmaxC，SC=Nmax，SCCPn，SC

PmaxD，SC=Nmax，SCDPn，SC

(7)

式中Pn,B，Pn,SC——电池和超级电容额定功率，MW；Nmax,BD——电池的最大放电脉冲系数，1.5～2。

而超级电容通常可以深度充放电，其最大充放电功率可达几倍甚至数十倍的额定额定功率，因此Nmax,SCC和Nmax,SCD数值较大。

2　互补储能系统的控制策略

2.1可再生能源发电系统的控制目标

可再生能源发电系统通过公共连接点与大电网连接，因此需要降低其输出功率的波动以减小对电网的冲击。对于安装在可再生能源出口侧的互补储能系统而言，在联络线功率给定时，需要实时跟踪发电功率变化，对功率波动进行平抑，最大限度地满足目标要求[9-10]。

控制目标：

min：f=[PT(t)+PESS(t)-PR(t)]2

(8)

式中PR(t)——t时刻可再生能源发电系统输出功率；PT(t)——联络线给定功率；PESS(t)——互补储能系统总功率，PESS(t)>0时表示放电，反之充电。

由于储能系统由蓄电池和超级电容器共同组成，于是有：

PESS(t)=PB(t)+PSC(t)

(9)

式中PB(t)，PSC(t)——互补储能系统中蓄电池和超级电容的充放电功率大小。

2.2储能系统的充放电控制策略

由于蓄电池储能的容量优势，适合平抑长期小功率波动，而超级电容具有功率密度大，能够应对尖峰大功率波动，并且响应速度快。结合二者能量和功率上的互补性，为可再生能源发电系统配置较大容量的蓄电池储能和小容量的超级电容储能，利用超级电容器作为蓄电池的功率辅助和缓冲器，在可再生能源发电系统功率平抑过程中出现大功率充放放电时，尽可能地优先使用超级电容，其他时刻主要使用蓄电池。这样既能发挥蓄电池平抑长期平稳小功率波动的优势，同时也能充分利用超级电容响应低频大功率波动的长处，这里采取如下控制策略来协调二者之间的配合：

2.2.1放电过程

由于超级电容最大允许放电功率远大于蓄电池最大允许放电功率，所以根据超级电容的剩余电量SOCSC实时信息采取如下放电控制：

(1)PESS(t)≥PSCDmax，即放电功率很大时，超级电容以最大放电功率来放电，剩余部分由蓄电池承担，于是有：

PSCD(t)=PSCmax

(10)

PBD(t)=PESS(t)-PSCmax

(11)

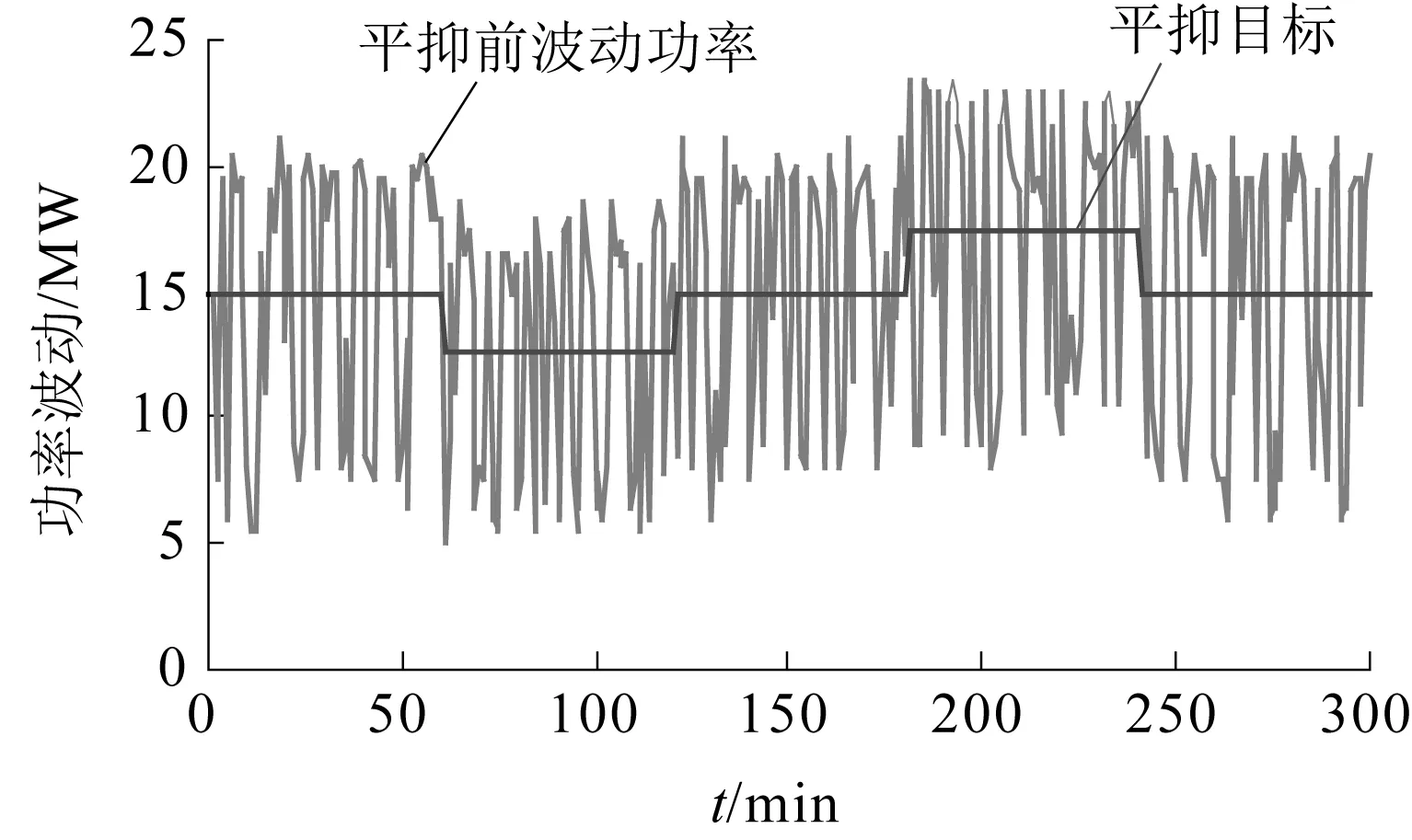
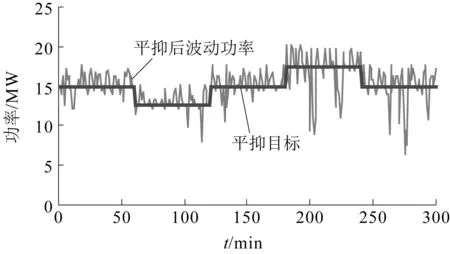
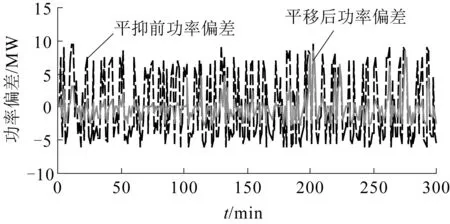
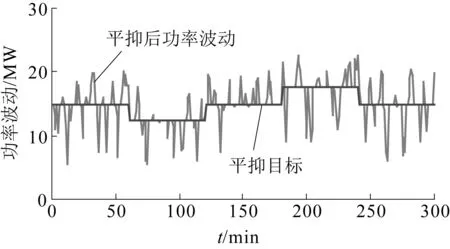
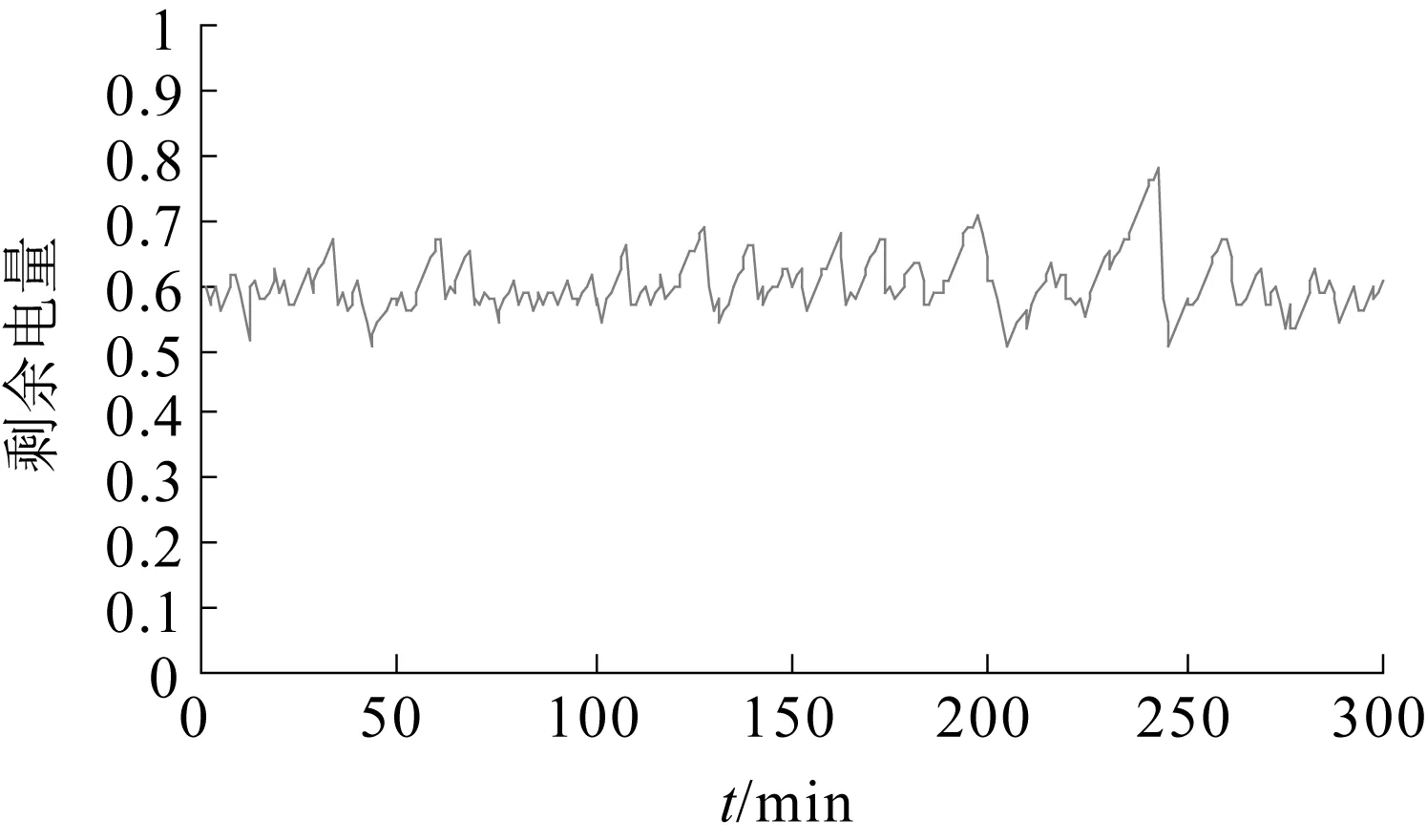
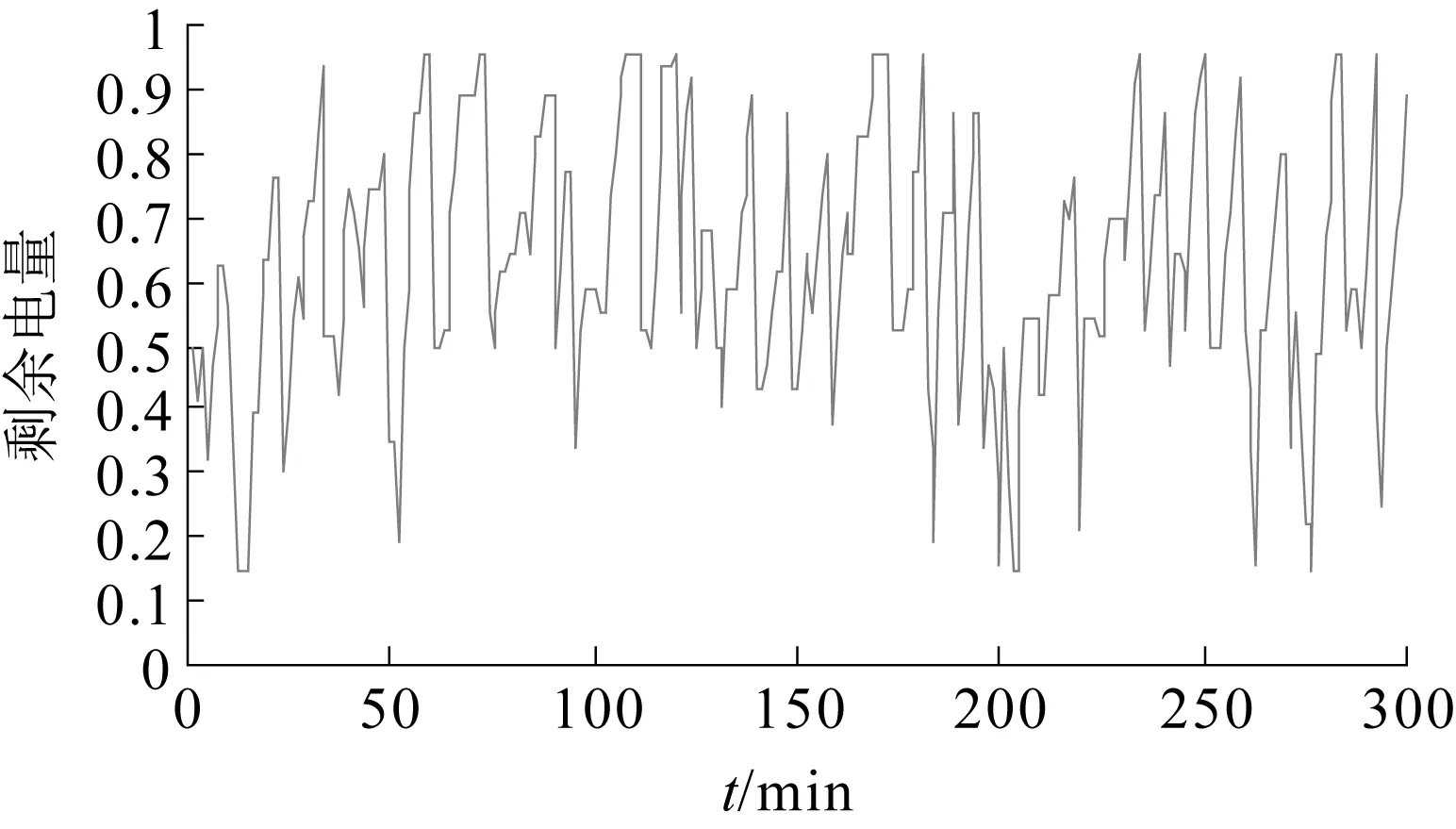
(2)PBmax≤PESS(t)

SOCSC≥0.8，即超级电容剩余电量比较大时，优先使用超级电容来放电，而蓄电池不工作，此时有：

PSCD(t)=PESS(t)

(12)

PBD(t)=0

(13)

SOCSC<0.8时，蓄电池使用其最大允许功率来放电，剩余部分由超级电容来辅助承担，此时有

PBD(t)=PBDmax

(14)

PSCD(t)=PESS(t)-PBD(t)

(15)

(3)PESS(t)

PBD(t)=PESS(t)

(16)

PSCD(t)=0

(17)

2.2.2充电过程

与放电过程相似，由于超级电容最大允许放电功率远大于蓄电池最大允许充电功率，在储能系统充电时，应根据超级电容的剩余电量SOCSC大小，协调而二者的充电功率分配，出现大功率充电时尽可能地使用超级电容。

(1)PESS(t)≤-PSCCmax，即充电功率很大时，超级电容以最大充电功率来充电，剩余部分由蓄电池承担，于是有：

PSCC(t)=-PSCCmax

(18)

PBC(t)=PESS(t)+PSCCmax

(19)

(2)-PSCCmax≤PESS(t)<-PBCmax，这时根据超级电容当前剩余电量分以下两种情况控制：

SOCSC≤0.4，即超级电容剩余电量较小时，优先使用超级电容来充电，剩余部分进入蓄电池，此时有：

PSCC(t)=PESS(t)

(20)

PBC(t)=0

(21)

SOCSC>0.4时，蓄电池以最大允许充电功率来充电，而剩余部分进入超级电容，此时有：

PBC(t)=-PBCmax

(22)

PSCC(t)=PESS(t)-PBC(t)

(23)

(3)PESS(t)>-PBCmax，即充电功率较小时，则直接使用蓄电池来充电，超级电容不工作，于是有：

PBC(t)=PESS(t)

(24)

PSCC(t)=0

(25)

式中PBC(t)，PBD(t)——t时刻蓄电池充电、放电功率；PBCmax，PBDmax——蓄电池的最大允许充电、放电功率；PSCC(t)，PSCD(t)——t时刻超级电容充电、放电功率；PSCCmax，PSCDmax——超级电容最大允许持续充电、放电功率；SOCSC、SOCB——超级电容和蓄电池的剩余电量。

通过控制策略，可以使得蓄电池始终工作在合理的充放电功率范围内，避免了深度充放电，而超级电容器根据实时的剩余电量情况，工作于大功率充放电场合，同时能够避免频繁工作容量上的不足。它们之间的配合有效缓解了蓄电池的充放电压力。

3　算例分析

选取某可再生能源发电系统为例，其输出功率以及联络线给定功率如图1所示。储能系统的参数如下：

(1) 蓄电池1参数：额定容量EB：3.28 MWh，最大持续充电功率为3.28 MW，最大持续放电功率为6.56 MW，蓄电池初始电量为SOCB(0)=0.6。

(2) 蓄电池2参数：额定容量EB：3.0 MWh，最大持续充电功率为3.0 MW，最大持续放电功率为6.0 MW，；蓄电池初始电量为SOCB(0)=0.6。

(3) 超级电容参数：额定容量EC：274.2 kW·h，最大持续充电功率为27.42×103kW，最大持续放电功率为27.42×103kW，超级电容初始电量为SOCSC(0)=0.5。

图1　可再生能源发电功率和联络线给定发电功率曲线

根据控制目标和储能系统模型中约束条件，进行了单一蓄电池、超级电容和二者联合组成的互补储能系统的仿真，结果如下。

3.1单一蓄电池储能系统仿真结果

选取蓄电池1作为储能系统，进行仿真，平抑后功率曲线以及蓄电池剩余电量SOCB分别如图2、图3所示。

图2　单一蓄电池储能平抑后功率曲线

图3　单一蓄电池储能系统平抑前后功率偏差对比

由图2、图3可以看出，当使用单一蓄电池储能系统时，平抑后的可再生能够能源发电系统输出功率与平抑目标相比，存在很大的波动，控制目标f=1 073.577 MW2，这并不是蓄电池容量配置不足引起的，而是由充放电功率上的限制造成的。由于蓄电池储能系统最大允许充放电功率的较小，在出现大功率充放电时，蓄电池不能够完全响应，许多平抑目标外的功率偏差不能被其消除。

单一蓄电池储能系统剩余电量SOCB变化曲线如图4所示。

图4　单一蓄电池储能系统剩余电量SOCB变化曲线

由图4可以看出，由于在平抑功率波动过程中，蓄电池多次以最大允许持续充放电功率工作，蓄电池的剩余电量SOCB整体变化较大，同时呈现了持续下降的趋势，这主要是因为蓄电池的最大允许充电功率较小，许多目标外的充电功率没能得到充分吸收，而最大允许放电功率较大，蓄电池整体呈现放电状态。

如若利用电池储能系统达到平抑目标，根据电池的初始电量SOCB(0)=0.6以及工作过程的最大充放电功率限制，至少需要配置的蓄电池容量为EB=6.0 MWh，这样会给整个储能系统造成一定的容量冗余。

3.2单一超级电容储能系统仿真结果

选取前面所给超级电容作为储能系统，平抑后功率曲线和超级电容SOCSC见图5、图6。

图5　单一超级电容储能系统平抑后功率曲线

图6　单一超级电容储能系统平抑前后功率偏差对比

图5、6表明，虽然超级电容的允许充放电功率大，目标外的功率偏差也都在其自身的功率约束范围内，但是因为超级电容容量上的限制，其大功率充放电的优势也没能得到完全的发挥。因此，整个可再生能源发电系统平抑的输出功率也存在很大的波动，控制目标f=2 191.347 MW2。

单一超级电容储能系统剩余电量SOCSC变化曲线如图7所示。

图7　单一超级电容储能系统剩余电量SOCSC变化曲线

由图7可以看到，在平抑功率波动的过程中，超级电容的SOCSC变化很大，频繁地达到0.95和0.15，这是因为容量上的不足使得其在经历短时的大功率充电或者放电，都非常容易地达到剩余电量SOCSC约束的上限或者下限。

如若利用超级电容储能系统达到平抑目标，根据超级电容的初始电量SOCSC(0)=0.6以及工作过程的电量约束，至少需要配置的超级电容容量为ESC=2.42 MW·h，由于超级电容高昂的成本，这样的配置是极其不合理的。

3.3互补储能系统仿真结果

以蓄电池2和超级电容联合构成互补储能系统，平抑后可再生功率输出功率如图8所示，互补储能系统中蓄电池和超级电容剩余电量分别如图9、图10所示。

图8　互补储能系统平抑后功率曲线

图9　互补储能系统中蓄电池SOCB变化曲线

图10　互补储能系统中超级电容SOCSC变化曲线

由图8可以看出，将蓄电池和超级电容联合组成互补储能系统后，与单一蓄电池储能系统相比，虽然整个储能系统的总容量基本相同，但是其平抑效果有了非常明显的改善，控制目标仅为f=2.073 3 MW2，平抑后的可再生能源输出功率几乎能够与平抑目标保持一致，只是在极少数时刻因为超级电容由于连续大功率工作容量限制，引起出现小功率的波动，但是功率波动最大只有0.5 MW。与单一超级电容或者蓄电池储能系统相比，互补储能系统之所以能够达到这种平抑效果，是因为通过所给充放电策略的有效协调了二者之间的配合：根据超级电容的实时剩余电量信息，在超过蓄电池最大允许充放电功率时尽可能地优先使用超级电容，这样就避免了蓄电池大功率充放电的可能性，整个储能系统中蓄电池始终工作在其功率的约束范围内，发挥其容量上的优势；超级电容主要应对尖峰大功率波动，最大限度地发挥了功率优势，而且工作在容量的约束范围之内，不会出现单一储能系统存在能量或者功率上的不足限制其难以达到平抑目标。

由图9表明，蓄电池的储能系统的剩余电量SOCB不仅始终在其约束范围内，同时由于超级电容在功率上的辅助，整个过程中SOCB是一个比较平稳的范围内变化，终止时刻蓄电池的剩余电量SOCB依然维持在0.6左右，能够保证下一个时间段的正常工作。而通过图10可以看出，由于超级电容是作为蓄电池大功率充放电的缓冲器，其剩余电量SOCSC变化较为剧烈，但是整个过程基本上也是维持在0.109 5的约束范围内，只有少数几个点由于连续充电达到了剩余电量上限。

4　结语

针对风力和太阳能构成的可再生能源系统发电功率波动问题，本文研究了蓄电池-超级电容互补储能系统，根据系统的平抑目标要求，给出了相应的协调控制策略，并且与单一蓄电池或者超级电容储能系统进行了对比。算例和仿真结果表明，互补储能系统具有明显的优势，可以在一定程度上克服蓄电池无法应对大功率波动而超级电容无法长时间持续工作的缺陷，充分发挥它们各自在能量、功率上的优势。

[1]张国驹，唐西胜，齐智平．平抑间歇式电源功率波动的混合储能系统设计[J]．电力系统自动化，2011，35(20)：24-28.

ZHANG Guo-ju,TANG Xi-sheng,QI Zhi-ping.Design of a Hybrid Energy Storage System on Leveling off Fluctuating Power Outputs of Intermittent Sources[J].Automation of Electric Power Systems,2011,35(20):24-28.

[2]张国驹，唐西胜，齐智．超级电容器与蓄电池混合储能系统在微网中的应用[J]．电力系统自动化，2010，34(12)：85-89.

ZHANG Guo-ju,TANG Xi-sheng, QI Zhi-ping.Application of Hybrid Energy Storage System of Super-capacitors and Batteries in a Microgrid[J].Automation of Electric Power Systems,2010,34(12):85-89.

[3]于芃，周玮，孙辉，等．用于风电功率平抑的混合储能系统及其控制系统设计[J]．中国电机工程学报，2011，31(17)：127-132.

YU Peng,ZHOU Wei,SUN Hui,et al.Hybrid Energy Storage System and Control System Design for Wind Power Balancing[J].Proceedings of the CSEE,2011,31(17):127-132.

[4]于芃，赵瑜，周玮，等．基于混合储能系统的平抑风电波动功率方法的研究[J]．电力系统保护与控制，2011，39(24)：35-40.

YU Peng,ZHAO Yu,ZHOU Wei,et al.Research on the method based on hybrid energy storage system for balancing fluctuant wind power[J].Power System Protection and Control,2011,39(24):35-40.

[5]丁明，林根德，陈自年，等．一种适用于混合储能系统的控制策略[J]．中国电机工程学报，2012，32(7)：1-7.

DING Ming,LIN Gen-de,CHEN Zi-nian,et al.A Control Strategy for Hybrid Energy Storage Systems[J].Proceedings of the CSEE,2012,32(7):1-7.

[6]DESHMUKH M K，DESHMUKH S S．Modeling of hybrid renewable energy system[J]． Renewable and Sustainable Energy Reviews，2008，12(1)：235-249.

[7]丁明，徐宁舟，毕锐．负荷侧新型电池储能电站动态功能的研究[J]．电力自动化设备，2011，31(5)：1-7.

DING Ming,XU Ning-zhou,BI Rui,et al.Dynamic model of new-type battery energy storage system at demand side[J].Electric Power Automation Equipment,2011,31(5):1-7.

[8]丁明，徐宁舟，林根德．电池储能电站静态功能的研究[J]．电工技术学报，2012，27(10)：242-247.

DING Ming, XU Ning-zhou, LIN Gen-de.Static Function of the Battery Energy Storage System[J]Transactions of China Electrotechnical Society,2012,27(10):242-247.

[9]丁明，徐宁舟，毕锐，等．基于综合建模的3类电池储能电站性能对比分析[J]．电力系统自动化，2011，35(15)：34-39.

DING Ming,XU Ning-zhou,BI Rui,et al.Modeling and Comparative Study on Multiple Battery Energy Storage Systems[J].Automation of Electric Power Systems,2011,35(15):34-39.

[10]张野，郭力，贾宏杰，等．基于平滑控制的混合储能系统能量管理方法[J]．电力系统自动化，2012，36(16)：36-41．

ZHANG Ye,GUO Li,JIA Hong-jie,et al.An Energy Management Method of Hybrid Energy Storage System Based on Smoothing Contro[J].Automation of Electric Power Systems,2012,36(16):36-41.

(本文编辑：赵艳粉)

Optimization Modeling and Control Strategy of Complementary Energy Storage System

WANG Bo

(State Grid Anhui Maintenance Company, Hefei 230061, China)

To solve the low power density problem of single battery energy storage system and low energy density problem of super-capacitor energy storage system, this paper proposed a complementary storage control strategy based on the combination of the two properties to maximize their strengths.And finally through mathematical modeling and the simulation, results show that the complementary energy storage system in supressing power fluctuatios of renewable energy generation system has obvious advantages.

Battery;Super-capacitor;Modeling;Contral Strategy

10.11973/dlyny201604013

王波(1988)，男，工程师，主要研究电网运行与控制，新能源发电技术，储能系统的优化建模与控制。

TM73

A

2095-1256(2016)04-0465-06

2016-03-11