数据融合与遗传算法在桥梁损伤辨识中的应用
2016-09-08孙诗裕俞阿龙张鹏鹏
孙诗裕, 俞阿龙, 赵 磊, 张鹏鹏
(1.南京工业大学 自动化与电气工程学院,江苏 南京 211816;2.淮阴师范学院 物理与电子电气工程学院,江苏 淮安 223300;3.宁夏大学 物理电气信息学院,宁夏 银川 750021)
数据融合与遗传算法在桥梁损伤辨识中的应用
孙诗裕1, 俞阿龙2, 赵磊3, 张鹏鹏1
(1.南京工业大学 自动化与电气工程学院,江苏 南京 211816;2.淮阴师范学院 物理与电子电气工程学院,江苏 淮安 223300;3.宁夏大学 物理电气信息学院,宁夏 银川 750021)
为了提高桥梁损伤识别的准确性,提出了基于数据融合和改进的多目标遗传算法对桥梁进行两段式的位置和程度辨识,通过灰色理论对桥梁的静态参数进行计算,得到静态位移曲率置信因子指标,以及模态分析理论对桥梁的动态参数进行计算,得到模态柔度曲率比指标,通过D-S证据对两种指标进行融合,确定损伤位置,提高结果的精度。再通过经过模糊优选理论改进的遗传算法,实现对损伤位置和程度的进一步辨识,实现对桥梁结构损伤位置和程度的分段式确定,提高了辨识的准确性。通过ANSYS软件建模仿真验证了该方法的有效性。
灰色理论; 模态分析; D-S证据; 遗传算法
0 引 言
针对桥梁的健康状况,如何对桥梁的损伤进行诊断已经成为一项重要的研究方向。朱宏平[1]验证了基于灰色理论的损伤位置识别方法的可行性。张军等人[2]使用柔度法对损伤位置进行识别,取得了较好的结果。韩乃杰、姜绍飞等人[3,4]将数据融合技术运用在损伤识别中提高损伤结果的精确度。张佳程等人[5]使用了遗传算法对损伤程度进行了识别,辨识结果令人满意。韩红飞等人[6]将采用应变模态差对管道进行损伤识别,取得了不错的效果。彭莉,毛春凤等人[7,8]将神经网络应用到结构损伤识别中去,识别效果明显。贾涛等人[9]结合有限元分析软件ANSYS对简支梁模型进行试验。Hong H M等人[10]运用实数编码的遗传算法对实际悬臂梁进行了损伤识别。杨维卫等人[11]对桥梁结构健康监测数据采集与传输做了深度研究。
常规的损伤识别方法有基于静态数据的静态识别法,有基于动态数据的动态识别法,还有基于智能检测技术的智能识别法。而这些方法都有各自的优点,但同时也存在着不足,如何利用多种损伤指标提高结果的准确性已经成为研究的一个重要方向,数据融合技术以其特有的优越性很好地解决了这一难题。对损伤程度的识别一直是研究的
一项重点,如何在确定损伤位置的前提下对损伤程度进行精确辨识,已经引起越来越多研究人员的关注,改进的遗传算法以其收敛速度快,精确度高等优点已经成功的应用到损伤程度识别领域。
1 基于灰色理论的静态位移曲率置信因子指标
1.1灰色信息系统
灰色信息系统是间于对内部特性已知的白色信息系统和对内部特性未知的黑色信息系统。灰色系统以“部分信息已知,部分信息未知”的“小样本”、“贫信息”的不确定系统为研究对象,通过对已知的信息进行处理开发,实现对未知信息的预测估计。桥梁系统可以看做一个典型的灰色系统,桥梁损伤前后的静态位移、静态应变参数是已知信息,桥梁的损伤状况是未知信息,可以通过静态位移、静态应变等参数构造关于桥梁损伤情况的关联系数,结构未发生损伤时,其节点的关联系数为1,当结构发生损伤时,损伤处的关联系数小于1,从而实现对损伤状况的辨识。
1.2静态位移曲率置信因子
令X为灰色关联因子集,x0∈X为未发生损伤的节点位移,x1∈X为结构发生损伤后的节点位移,静态位移曲率置信因子(SDCACi)为
(1)
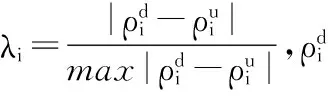
=((α1(x0(i+1))-α1(x0(i)))/Δxi)/Δxi
α1(x0(i))=x0(i+1)-x0(i)
=((α1(x1(i+1))-α1(x1(i)))/Δxi)/Δxi
α1(x1(i))=x1(i+1)-x1(i)
(2)
2 基于模态参数的柔度差曲率比指标
利用结构的模态参数如模态频率,模态振型计算结构各个节点的柔度差曲率比,柔度只需要得到前几阶的振型和频率,因此具有更好的实用性,因为在实际工程运用中高阶振型和频率往往是很难获得的。结构部分位置发生损伤后,会导致该部分刚度下降,柔度增加,可以用此进行判别
(3)
式中ωi为第i阶频率,Φ={φ1,φ2,…,φn}为振型矩阵,φi为第i阶振型。
Γ=Fd-Fu,Γ为结构的柔度差矩阵,单纯地实用柔度差作为损伤辨识的指标,其判别不够清晰,因此使用柔度差曲率比作为动态损伤测量指标
(4)
式中M为柔度差矩阵的主对角元素的曲率,Mu为为损伤柔度矩阵的主对角元素曲率
δf″i=(δfi+1-2δfi+δfi-1)/(li-1li)2
(5)
式中fi为主对角元素第i个值。
3 数据融合实现方法
数据融合技术将对同一个目标的多个检测信息加以处理,得出更为准确的结果,本文将通过静态识别法得到的静态位移曲率置信因子指标与通过动态识别法得到的柔度差曲率比指标进行融合处理,融合目的是为了降低单一融合指标的误差,凸显损伤位置峰值,使最后结果更为准确。融合方法选用经典的D-S证据理论,D-S证据理论能够处理集合的不确定性。设m1和m2分别是两组信息源对应的基本概率赋值,焦元分别为A1,A2,…,An和B1,B2,…,Bn,设
(6)
两信息源的组合为
m(C)=
(7)
4 基于模糊优选理论的改进多目标遗传算法
由于传统的遗传算法存在收敛速度慢,局部搜索能力差的不足,提出了一种基于模糊优选理论的改进遗传算法。多目标模糊优选的最优解应包含各个子目标的贡献,应包含在一模糊集合之中,此模糊集合的隶属函数为
(8)
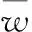
使此集合的隶属函数取得最大值的解就是多目标模糊优化的最优解,即求
r(α*)=max|r(α)|
(9)
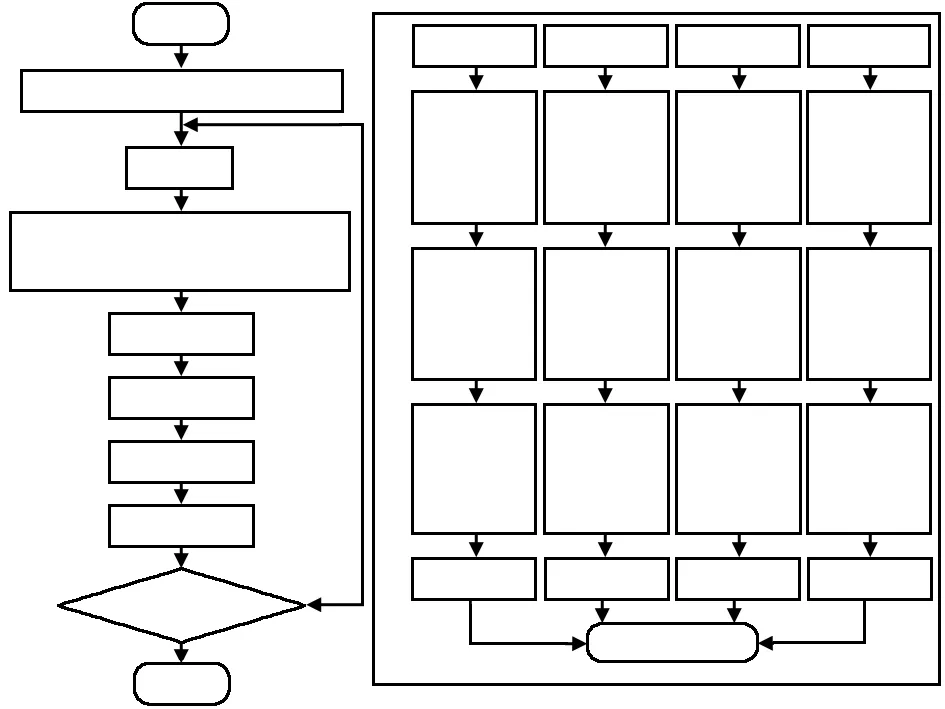
图1 改进多目标遗传算法流程图
5 仿真实验
5.1模型建立
利用有限元分析软件ANSYS建立一个21个节点,20个单元的简支梁模型,混凝土材料选用C50,弹性模量为3.45×1010Pa,泊松比为0.17,材料密度为2 500kg/m3,横截面为20mm×20mm。通过改变单元的弹性模量模拟损伤
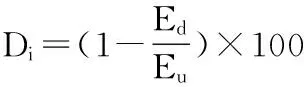
(10)
式中Ed为损伤后单元的弹性模量,Eu为损伤前单元的弹性模量。
5.2单损伤识别
改变第15单元的弹性模量,损伤程度为20 %。首先对简支梁进行静力分析,对节点1和节点21进行全约束,对梁施加第11节点施加10 kN向下方向力,分析结构损伤前和第15单元损伤后的位移情况。
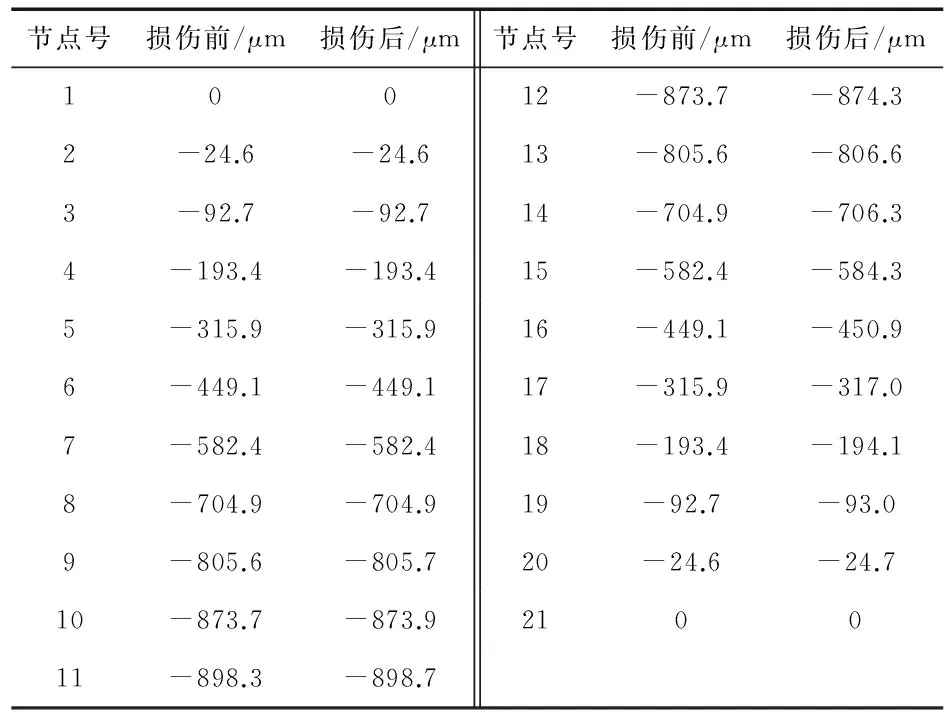
表1 损伤前后各个节点的y方向位移
再利用ANSYS软件对简支梁进行模态分析,分别提取前三阶频率和前三阶y方向模态振型,提取结果部分如表2。
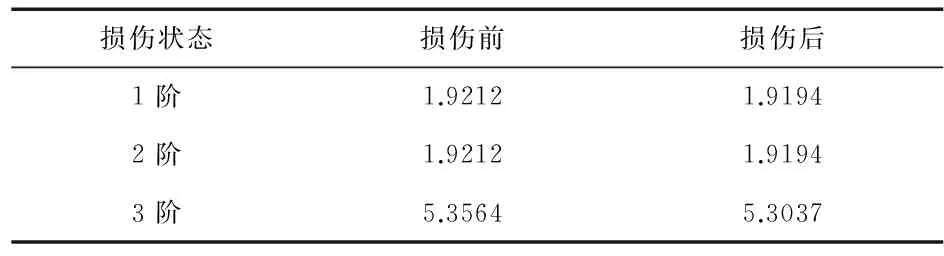
表2 损伤前后前3阶频率
将提取的参数运用上文的识别方法和 融合方法在仿真软件Matlab环境下进行仿真实验,得到损伤识别结果如图2~图4。
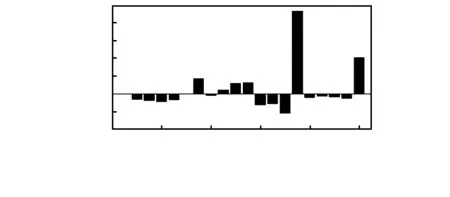
图2 柔度差曲率比
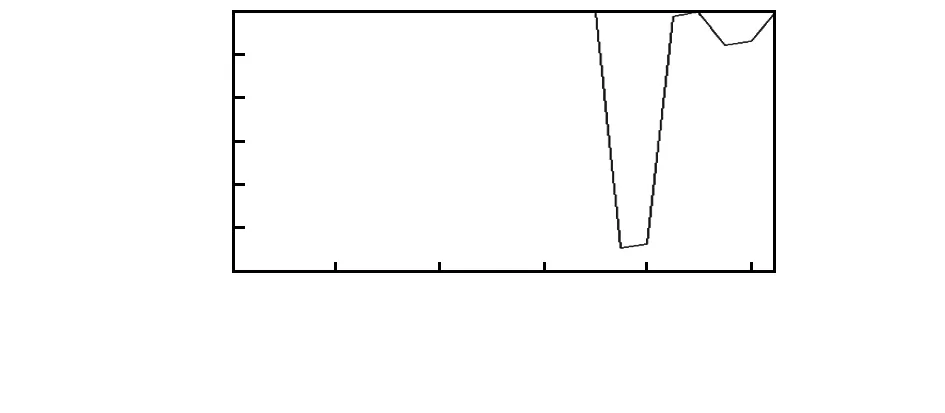
图3 静态位移曲率置信因子
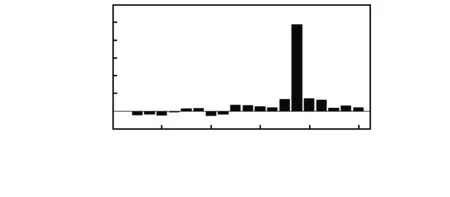
图4 融合结果
由图3可以看出利用柔度差曲率比指标在15单元的值接近1,明显高于其余单元,但20单元的值接近0.5,这也是不能忽略的部分,所以初步认定损伤部分在15单元和20单元。
由图4可以看出节点15的置信因子为0.45左右,节点16的置信因子为0.46左右,可以初步判定节点15与节点16直接的第15单元有损伤,但节点19,节点20处的置信因子也不为1,所以利用单一的损伤指标很容易出现误判,再利用数据融合技术对上述两种指标进行融合处理。首先对静态位移曲率置信因子进行简单的处理,因为置信因子为1代表了无损伤,小于1代表了可能存在损伤,这与柔度差曲率比的判别方法不同,用1减去置信因子,得到结果就与柔度差曲率比判别方法一样,再将两种指标代入D-S证据理论的公式中,得到的结果如图5,可以清楚看到,融合后的指标相比较于融合前的指标在损伤位置更为突出,未损伤位置的值很小,发生误判的几率更小,所以,通过数据融合技术将多种损伤指标进行融合处理可以很好的提高损伤辨识的精确性。
5.3多损伤识别
利用ANSYS软件改变简支梁的第6和第15单元的弹性模量模拟损伤,其中第6单元损伤程度为15 %,第15单元损伤程度为20 %。分别提取静态位移、模态振型和频率,代入公式求得损伤辨识情况如图5~图7。
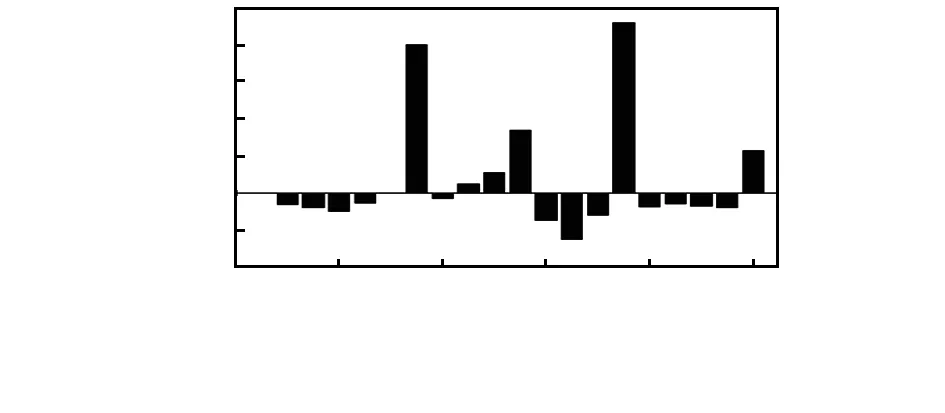
图5 柔度差曲率比
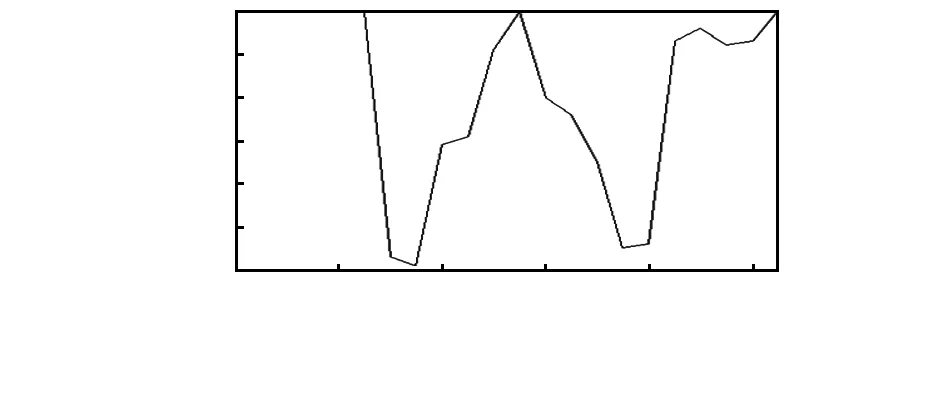
图6 静态位移曲率置信因子
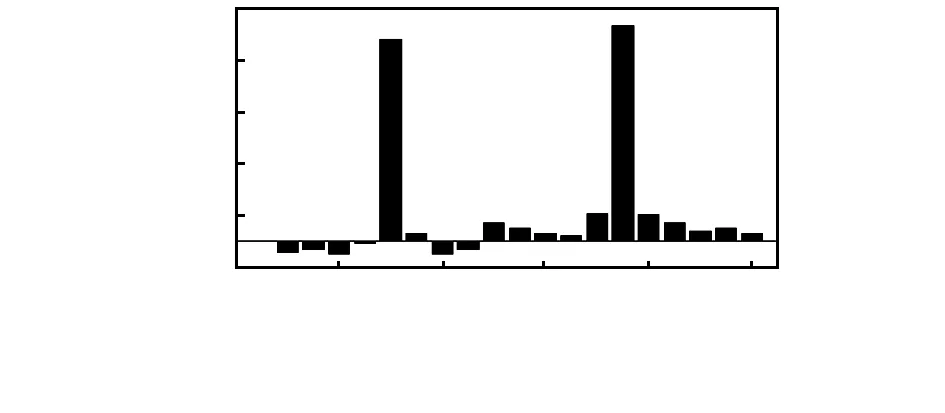
图7 融合结果
从上图可以看出,单一的损伤指标也可以判别出多损伤具体位置,但通过D-S证据理论融合后的结果更为准确。验证了数据融合在单损伤,多损伤识别中得到了有效地运用。
5.4损伤程度识别
利用改进的遗传算法进行损伤程度识别,以各损伤单元应变残差最小为优化目标建立优化目标函数,群体规模为100,交叉概率设为0.3,变异概率为0.08,以适应值的相对优属度大小对群体中各个个体进行并列选择,对梁的损伤程度进行辨识,收敛条件为群体中识别的各单元损伤最大值与最小值差小于1 %。识别结果如图8。
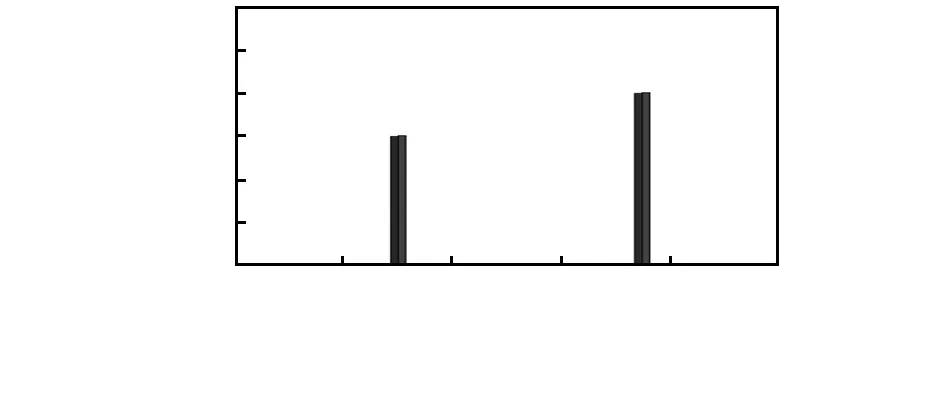
图8 6单元15 %损伤和15单元20 %损伤
从图8可以看出:预设损伤为20 %,通过改进的遗传算法得到的损伤程度为19.98 %。图8中6单元预设损伤程度为15 %,识别的程度为15.03 %,15单元损伤预设的损伤程度为20 %,识别的损伤程度为20.03 %。通过结果可以得到,改进的遗传算法具有良好的损伤程度识别功能。
5.5传统遗传算法和改进的多目标遗传算法比较
从表3中可以看出,传统的遗传算法无论对单损伤还是多损伤都需要500多代的运算才能满足条件,而改进的遗传算法仅需要200代左右就可以达到相同的精度。而且从群体均值变化可以看出,改进的多目标遗传算法收敛速度更快,运算效率更高。
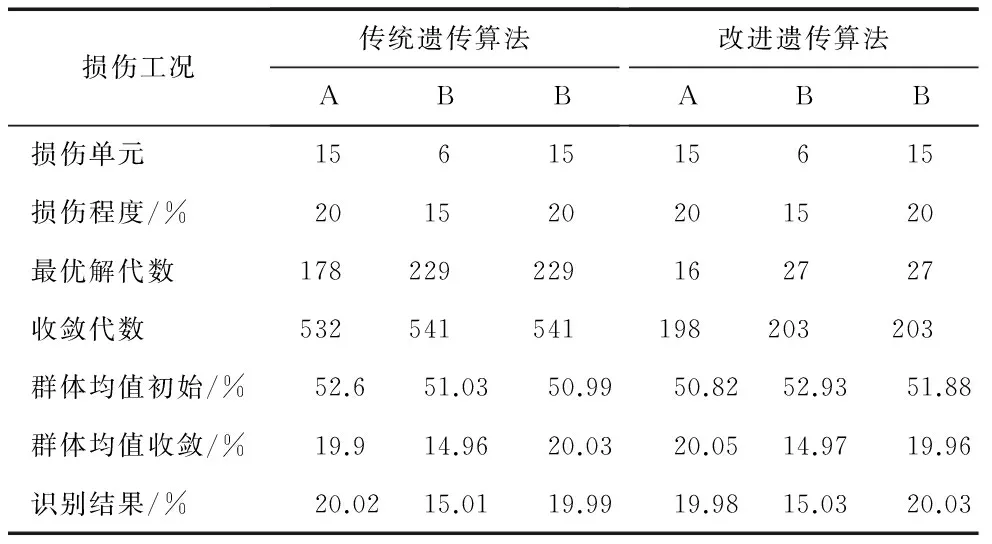
表3 传统遗传算法与改进遗传算法
6 结 论
本文主要通过ANSYS建立一个两端固定的简支梁模型来模拟研究,验证了静态位移曲率置信因子和柔度差曲率比两种损伤指标,并通过数据融合技术进一步融合处理,通过数值计算和理论分析得到以下结论:
1)柔度法会出现误判的结果,静态位移曲率置信因子相对精确度更高。
2)通过数据融合得到的结果精确度相比较于单一的损伤指标要高很多,通过将静态数据指标与动态数据指标相融合,得到的损伤结果图抗干扰能力更强。
3)通过遗传算法对损伤程度识别,能够达到理想的精度,改进的算法相比较于传统的算法收敛速度更快,效率更高,这在大型结构的损伤辨识中效果更为理想。
[1]朱宏平.结构损伤检测的智能方法[M].北京:人民交通出版社,2009:180.
[2]张军,刘建勋,徐进,等.结构损伤诊断的模态柔度差曲率法[J].工程力学 ,2011(12):112-119.
[3]韩乃杰,张浩,吴向飞.基于应变模态的桥梁损伤识别方法研究进展[J].中外公路,2015(2):90-95.
[4]姜绍飞,胡春明.基于模态指标与数据融合的钢管混凝土拱桥损伤识别[J].振动与冲击,2009(12):19-25.
[5]张佳程,周邵萍,苏永升.基于数据融合与单纯形遗传算法的管道损伤识别[J].华东理工大学学报,2015(2):132-137.
[6]韩红飞,周邵平,郝占峰.基于应变模态差的管道损伤辨识仿真[J].振动、测试与诊断,2013(5):210-213.
[7]彭莉,李兆.基于模态应变能和神经网络的分步损伤诊断法[J].公路与汽运,2008(8):117-120.
[8]毛春凤,顾永强.基于模态应变能与神经网络的桥梁损伤识别研究[D].包头:内蒙古科技大学,2013:1-70.
[9]贾涛,刘世忠.基于ANSYS实体模型对小跨径钢筋混凝土简支梁旧桥的模态分析[J].兰州交通大学学报,2008(6):9-15.
[10] Hong H M,Youg Xia.Vibration-based damage detection of structures by genetic algorithm[J].Journal of Computing in Civil Engineering,2002,16(3):222-229.
[11] 杨维卫,俞阿龙.基于WSNs和移动Agent的桥梁结构健康监测研究[J].传感器与微系统,2013,31(12):78-81.
作者简介:
俞阿龙,通讯作者,E—mail:yal@hytc.edu.cn。
Application of data fusion and genetic algorithm in damage identification of bridge
SUN Shi-yu1, YU A-long2, ZHAO Lei3, ZHANG Peng-peng1
(1.School of Automation and Electrical Engineering,Nanjing University of Technology,Nanjing 211816,China; 2.School of Physical and Electronic and Electrical Engineering,Huaiyin Normal University,Huai’an 223300,China; 3.School of Physics Electrical Information,Ningxia University,Yinchuan 750021,China)
In order to improve the accuracy of bridge damage identification,based on data fusion and improved multi-objective genetic algorithm are proposed,applied for two section location and extent recognition on bridge,by gray theory,calculate static parameters of bridge,and obtain static displacement curvature confidence factor index,and modal analysis theory to calculate dynamic parameters of bridge,and obtain modal flexibility curvature ratio index,through D-S evidence,fuse two kinds of indexes to determine damage position,improve precision of results.Again by the improved genetic algorithm and fuzzy optimization theory,realize damage position and extent identification,implement sectional determination bridge structure damage location and extent,improve accuracy of identification. Through ANSYS software modeling and simulation,verify effectiveness of the proposed method.
gray theory; modal analysis; D-S evidence; genetic algorithm
10.13873/J.1000—9787(2016)09—0152—04
2015—10—26
TU 317
A
1000—9787(2016)09—0152—04
孙诗裕(1990-),男,江苏盐城人,硕士研究生,主要研究方向为检测技术与自动化装置,无线传感器网络。
