高超声速强机动目标改进IMM-CKF跟踪算法*
2016-09-08戴邵武张文广
戴邵武, 方 君, 张文广, 邹 杰
(1.海军航空工程学院 控制工程系,山东 烟台 264001;2.海军航空工程学院 研究生管理大队,山东 烟台 264001;3.中国航空工业集团 光电控制技术重点实验室,河南 洛阳 471009)
高超声速强机动目标改进IMM-CKF跟踪算法*
戴邵武1, 方君2, 张文广1, 邹杰3
(1.海军航空工程学院 控制工程系,山东 烟台 264001;2.海军航空工程学院 研究生管理大队,山东 烟台 264001;3.中国航空工业集团 光电控制技术重点实验室,河南 洛阳 471009)
高超声速强机动目标的运动具有复杂性、突变性和强非线性特点,针对单模型算法难以实现对此类目标的精确跟踪,提出一种改进的交互多模型(IMM)算法,克服了单模型算法跟踪强机动目标的缺陷和标准IMM算法对似然函数计算不准确的问题,实现了不同子模型之间的变维交互;采用容积卡尔曼滤波(CKF)算法实现了雷达观测数据与目标状态量之间的高精度非线性转换。仿真结果表明:改进的IMM算法相比单模型算法和标准的IMM-CKF算法,明显提高了高超声速强机动目标的跟踪精度。
交互多模型; 容积卡尔曼滤波; 高超声速强机动目标; 目标跟踪
0 引 言
近年来出现的以美军X—43,X—51为代表的高超声速强机动目标[1,2],目标机动具有突发性和复杂性,运动过程会出现匀速、加速、转弯甚至加加速等多种状态,跟踪难度更大。机动目标跟踪的关键在于目标模型的构建和基于该模型滤波算法的实现[3],因此,需要针对高超声速强机动目标的机动特点建立目标模型并选择滤波算法。
针对目标模型构建,学者们提出了CV,CA非机动模型以及Singer,CS等机动模型[3],但这些模型的维数过低,对高超声速强机动目标的跟踪效果较差。1997年,Kishore借鉴Singer模型,首次提出了Jerk模型算法[4],其主要应用价值在于强机动目标的跟踪,只是由于加加速度变化会导致加速度的不断变化,使得该模型对弱机动目标的跟踪并不理想,在其基础上乔向东等人建立了CS-Jerk模型,改善了Jerk模型的跟踪性能[5]。然而上述算法都是基于单模型的,由于单模型难以准确描述此类目标运动状态的变化,当模型不匹配时,易导致滤波发散,目标的跟踪误差将会很大。1984~1989年,Blom和Bar-Shalom Y在广义伪贝叶斯算法基础上,首次提出了一种具有Markov转移概率的结构自适应算法——交互多模型(interacting multiple model,IMM)算法,极大地克服了单模型算法的不足与缺陷[6],然而标准的IMM算法选择的子模型往往维数相同或是同一模型[7~9],没有考虑子模型维数不同时的交互问题[10],模型集不适用于高超声速强机动目标。
IMM算法中另一个关键问题是滤波器的选择,目标的量测数据是由雷达观测得到的极坐标数据,而系统模型是在直角坐标系下建立的,需要进行非线性转换。EKF是最早提出的非线性滤波算法,却只适用于解决弱非线性问题,对于强非线性问题,易导致滤波发散。基于UT变换的UKF是对非线性概率密度进行逼近,比EKF精度更高,但其滤波性能取决于滤波参数的选择[11]。基于容积规则的CKF比UKF的非线性逼近能力更高,滤波稳定性更好[12],理论推导更为严格,且滤波器中无滤波参数[13]。
本文考虑高超声速强机动目标的机动特点,提出一种高超声速强机动目标IMM-CKF跟踪算法。仿真结果表明:相比CS-Jerk算法和IMM-CKF算法,改进的IMM-CKF算法显著提高了对高超声速强机动目标的跟踪精度。
1 CKF算法
假设非线性系统描述如下
(1)
式中f(·)和h(·)分别为系统方程和量测方程,Xk和Zk分别为k时刻n维系统状态向量和m维量测向量,Wk和Vk分别为状态噪声和量测噪声向量,其协方差阵分别为Qk和Rk。
CKF滤波的步骤如下:
1)初始化
2)时间更新
滤波协方差矩阵分解,即
(2)
计算求积点,即
(3)
传播求积分点,即
ξi,k+1|k=f(ξi,k|k)
(4)
状态预测,即
(5)
状态预测协方差矩阵,即
(6)
3)量测更新
矩阵分解,即
(7)
计算求积分点,即
(8)
求容积点传播,即
εi,k+1|k=h(ξi,k+1|k)
(9)
量测值预测,即
(10)
预测误差协方差,即
(11)
估计互协方差矩阵,即
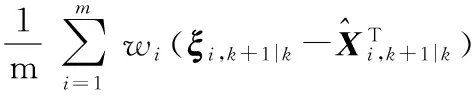
(12)
计算卡尔曼增益,即
(13)
状态更新,即
(14)
状态协方差矩阵更新,即
(15)
2 改进的IMM-CKF算法
2.1IMM算法模型集的选择
本文选择CV,CS和CS-Jerk模型组成模型集,CV,CS模型具体算法见文献[3], CS-Jerk模型在Jerk模型的基础上借鉴“当前”统计模型的思想,认为将目标的加加速度假设为零均值的时间相关过程是不符合实际的,对Jerk模型进行改进,将加加速度的一步预测值x…(k+1/k)作为当前时刻加加速度的均值,从而使得对模型中加加速度的估计更加符合机动目标的实际运动过程,算法的具体步骤见文献[5]。
2.2IMM-CKF算法
假设IMM算法具有r个模型,则其离散时间状态方程和量测方程为
Xk+1=FjXk+Wj,k,j=1,2,…,r
(16)
Zk=HjXk+Vj,k,j=1,…,r
(17)
式中Fj为模型j的状态转移矩阵,Wj,k为均值为零,协方差矩阵为Qj,k的系统噪声;Hj为模型j的观测矩阵,Vj,k为均值为零,协方差矩阵为Rj,k的量测噪声。
马尔可夫转移概率矩阵为
(18)
则交互式多模型算法从k-1时刻到k时刻的递推过程包括:
1)状态估计的交互输入
(19)
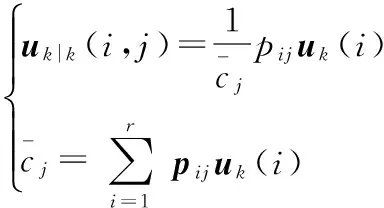
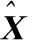
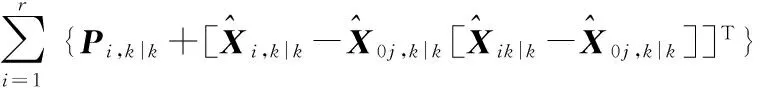
uk|k(i,j)
(20)
2)模型修正
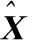
3)模型概率更新
对于第j个模型,k时刻其最大似然函数如下
(21)
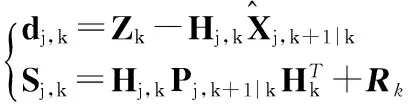
模型j对应的后验概率为
(22)
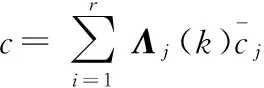
4)模型融合输出
k时刻模型交互式输出为
(23)
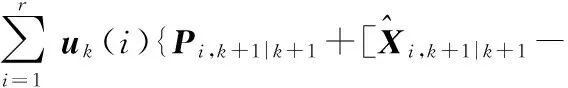
(24)
2.3改进的IMM算法
(25)
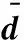
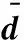
3 仿真实验
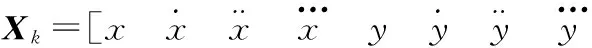
系统量测方程为
(26)
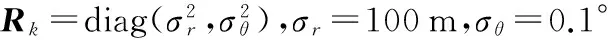

表1 x方向目标的机动情况

算法的跟踪性能指标可以通过位置和速度估计值的均方根误差(RMSE)和平均误差(AE)来评价,其表达式分别为
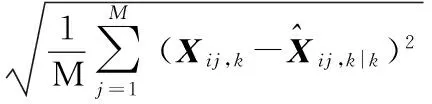
(27)
(28)
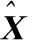
图1给出了目标真实运动轨迹和采用改进IMM-CKF算法目标的跟踪轨迹,图2、图3为x方向上目标位置和速度估计的均方根误差曲线,图4、图5为y方向上目标位置和速度估计的均方根误差曲线,表2给出了目标状态估计值的平均误差。
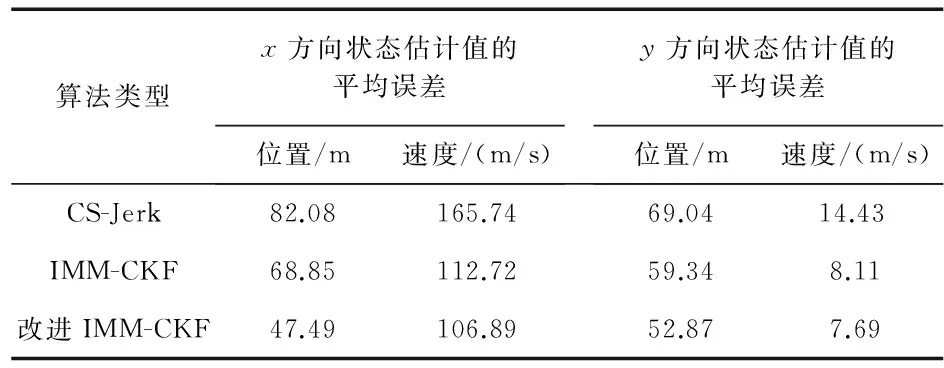
表2 x,y方向状态估计平均误差
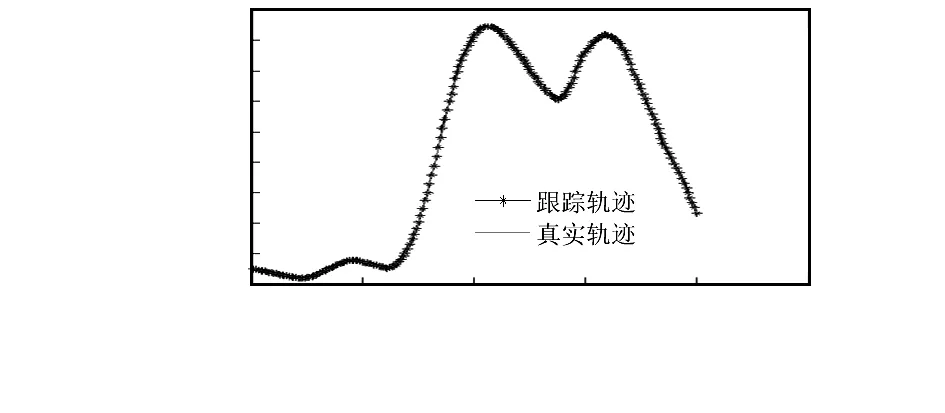
图1 目标跟踪轨迹与真实轨迹
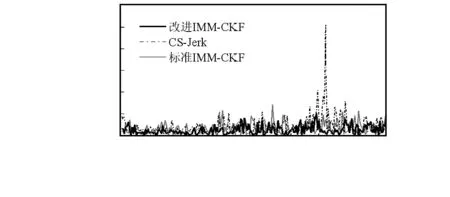
图2 x方向目标位置估计均方根误差
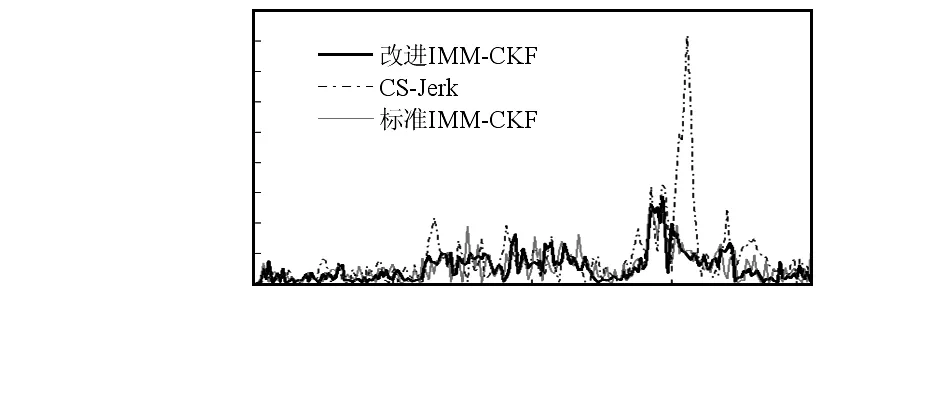
图3 x方向目标速度估计均方根误差
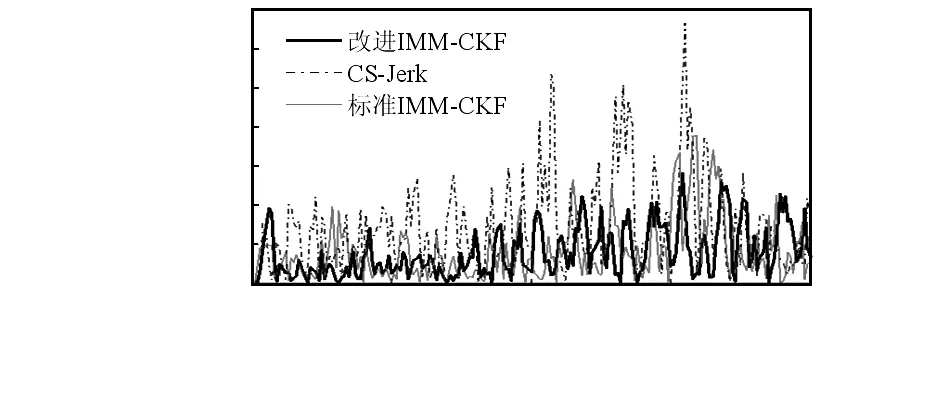
图5 y方向目标速度估计均方根误差
4 结 论
本文通过分析高超声速强机动目标的机动特点和单模型算法跟踪强机动目标时的缺陷,提出一种适用于高超声速强机动目标的IMM算法。该算法充分考虑了目标可能出现的各种机动情形,选择CV,CS和CS-Jerk模型作为模型集,并改进了标准IMM算法;其次,系统模型是高维的,而CKF算法对高维状态向量的估计精度跟高,且滤波稳定性好,故选择CKF进行滤波计算。仿真结果表明:本文提出的改进IMM-CKF算法实现了对高超声速强机动目标的高精度跟踪。
[1]张翔宇,王国宏,李俊杰,等.临近空间高超声速滑跃式轨迹目标跟踪技术[J].航空学报,2015,36(6):1983-1994.
[2]肖松,谭贤四,王红,等.变结构多模型临近空间高超声速飞行器跟踪算法[J].红外与激光工程,2014,43(7):2362-2370.
[3]何友,修建娟,关欣.雷达数据处理及应用[M].北京:电子工业出版社,2013.
[4]Mehrotra K,Mahapatra P R.A Jerk model for tracking highly maneuvering targets[J].IEEE Transactions on Acrosspace and Electronics Systems,1997,33(4):1094-1105.
[5]Qiao Xiangdong,Wang Baoshu,Li Tao.A motion model for tra-cking highly maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems,2002,6(3):493.
[6]Bar-Shalom Y,Li X R,Kirubarajan T.Estimation with application to tracking and navigation:Theory algorithms and software[M].New York:John Wiley & Sons,2004.
[7]谭顺成,王国宏,王娜.IMM-Singer模型的机动目标跟踪算法[J].火力与指挥控制,2012,37(2):32-34.
[8]陈海,单甘霖.基于IMMCKF的机动目标跟踪算法[J].电光与控制,2011,18(10):1-5.
[9]张云雯,姚景顺,董天忠.IMM模型组的选择与参数的设定[J].系统仿真学报,2013,25(4):849-854.
[10] 毛少锋,冯新喜,刘玉磊,等.变维自适应交互式多模型跟踪算法[J].电光与控制,2015,22(2):36-40.
[11] Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[C]∥Proceedings of the IEEE,2004:401-422.
[12] Arasaratnam I,Haykin S,Hurd T R.Cubature Kalman filtering for continuous-discrete systems:Theory and simulations[J].IEEE Transactions on Signal Processing,2010,58(10):4977-4993.
[13] 孙枫,唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J].控制与决策,2013,28(2):303-308,312.
[14] 陈映,程臻,文树梁.适用于模型失配时的改进IMM算法[J].系统工程与电子技术,2011,33(12):2593-2597.
Modified IMM-CKF tracking algorithm for highly maneuvering hypersonic target*
DAI Shao-wu1, FANG Jun2, ZHANG Wen-guang1, ZOU Jie3
(1.Department of Control Engineering,Naval Aeronautical and Astronautical University,Yantai 264001,China;2.Department of Scientific Research,Naval Aeronautical and Astronautical University,Yantai 264001,China;3.Science and Technology on Electron-optic Control Laboratory,Aviation Industry Corporation of China,Luoyang 471009,China)
The movement of highly maneuvering hypersonic target has characteristics of complexity,mutability,and strong nonlinearity,aiming at the problem that single model algorithm is difficult to track such targets,a modified interacting multiple model(IMM) algorithm is proposed,this algorithm overcomes the shortage of single model algorithm tracking highly maneuvering target and normal IMM algorithm calculating likelihood function inaccurately,realizes variable dimension interaction of different sub models; cubature Kalman filtering(CKF) algorithm is used to complete high-precision nonlinear transform of radar measurement data and target states.The simulation results show that compared with single model algorithm and normal IMM algorithm,the modified IMM-CKF algorithm obviously improves tracking precision of highly maneuvering hypersonic target.
interacting multiple model(IMM); cubature Kalman filtering(CKF); highly maneuvering hypersonic target; target tracking
10.13873/J.1000—9787(2016)09—0133—04
2015—10—23
国家自然科学基金资助项目 (61203168); 航空科学基金资助项目(20135184007)
TN 953
A
1000—9787(2016)09—0133—04
戴邵武(1966-),男,湖南邵阳人,博士,教授,研究方向为惯性技术与组合导航。
