具有模型概率修正的新颖IMMPDA算法*
2016-09-08王美健吴小俊
王美健, 吴小俊
(江南大学 物联网工程学院,江苏 无锡 214122)
具有模型概率修正的新颖IMMPDA算法*
王美健, 吴小俊
(江南大学 物联网工程学院,江苏 无锡 214122)
为了有效提高杂波环境中机动目标跟踪的精度,将标量交互式多模型(SIMM)算法与概率数据关联(PDA)算法结合成SIMMPDA算法。其中,PDA算法能够有效处理杂波环境下的数据关联与测量不确定性。SIMM算法处理运动模型间的切换,且在线性最小方差意义下获得目标的最优状态估计。而考虑因杂波的干扰导致各时刻的匹配模型占优程度不明显的问题,故再对各时刻SIMMPDA算法所得的后验模型概率进行修改,得到一个基于模型概率修改的SIMMPDA算法,即为M-SIMMPDA算法。仿真结果表明,所提算法的跟踪精度得到一定程度的提高。
机动目标跟踪; 标量交互式多模型; 概率数据关联
0 引 言
在实际的跟踪系统中,往往存在许多杂波干扰,造成测量源的不定性,使跟踪问题变得复杂。针对杂波环境下的目标跟踪问题,一系列有效算法相继被提出,主要包括最近领域标准滤波器[1]、最强邻域法[2]、概率最近邻域法[3]、概率数据关联(PDA)[4]算法、综合概率数据关联 (IPDA) 算法[5,6]及联合概率数据关联(JPDA)算法[7~9]等。而其中的PDA,IPDA与JPDA都是先对当前时刻不同的确认量测来自目标的概率进行计算,再利用这些概率进行加权以获得目标的状态估计。其中PDA算法是在杂波环境中进行单目标跟踪较好的数据关联算法,但是它不能较好地用于跟踪机动目标。而交互式多模型(IMM)[10]算法在机动目标跟踪领域有着良好的性能,将IMM算法与PDA算法结合的IMMPDA算法[11,12]已成为杂波环境中跟踪单机动目标的主要算法。该算法无需进行机动检测,跟踪精度相较于其他数据关联算法更高。
对于IMMPDA算法来说,其中的PDA算法用于处理落入相关波门内的候选测量,由于各测量与目标的关联概率不同,其在目标状态估计中的作用也就不一样,这样在进行目标状态估计时,将无法确认来源的测量集都利用上了。IMM算法主要是以一组不同模型描述目标运动过程,模型间的切换服从马尔可夫过程,通过加权各模型滤波器输出作为目标运动状态的最终估计。而SIMM[13,14]算法作为一个改进的IMM算法,是在线性最小方差意义下获得目标的最优状态估计,已在文献[13]里较之IMM算法体现出了其性能优势。因此,本文提出一种新的IMMPDA算法,该算法由SIMM算法与PDA算法结合以适应杂波环境里的机动目标跟踪,并考虑到杂波干扰导致各时刻匹配模型的占优程度弱的问题,而对各时刻各模型的后验概率进行修改[15],以期望提高匹配模型的占优程度,进而提高目标跟踪的精度。仿真实验表明:在杂波环境中跟踪机动目标,所提算法的性能得到了明显的改善。
1 线性系统描述
目标的运动方程

(1)
传感器的测量方程
zk=Hxk+vk
(2)
式中x为n维状态向量,z为观测向量,F为状态转移矩阵,G为过程噪声分布矩阵,H为量测矩阵。v为标准测量噪声向量,w为过程噪声向量,v和w是互不相关的零均值高斯白噪声向量,其协方差矩阵分别为R和Q。
模型的跳变规律服从马尔可夫链,即为
(3)
2 模型概率修改操作
一般来说,多模型算法在各时刻中的匹配模型相对占优于其他不匹配模型,即匹配模型概率较大于不匹配模型概率,模型概率修改操作[15]旨在通过修改模型概率来提高匹配模型的占优程度。假定模型概率向量为
(4)
各循环周期使用修改操作Φ(·)修改uk
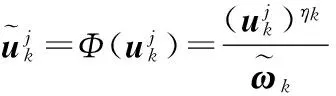
(5)
式中ηk为一个修改参数,用于控制修改程度,归一化常数为
(6)
1)如果s>2,有
(7)
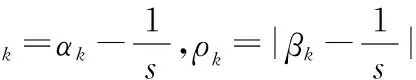
2)如果s=2,有
(8)
式中λk为一个阈值。
3 所提出的M-SIMMPDA算法
该算法先将SIMM算法与PDA算法结合,并对各模型后验概率进行修改操作,这样既使得算法能够在机动目标跟踪过程中有效处理杂波问题,也缓解杂波干扰造成的匹配模型占优弱的问题。
算法的一个循环周期步骤(算法的结构流程图如图1所示)。
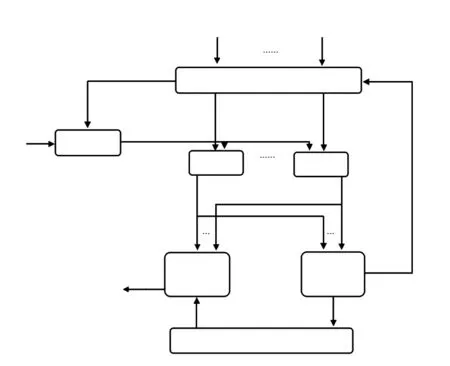
图1 M-SIMMPDA算法的结构

1)混合权重计算(i,j=1,2,…,s)
(9)
2)混合(i,j=1,2,…,s)
(10)
(11)
3)PDA滤波(j=1,2,…,s)
预测
(12)
(13)
(14)
(15)
测量确认(使用模型概率加权门(MPWG[16])来确认候选测量):
当且仅当
(16)
式中
(17)
(18)
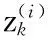
(19)
式中n2为量测的维数(Cn2为同维单位超球的体积,即C1=2,C2=π,C3=4π/3等)
(20)
(21)
(22)
(23)
(24)
(25)
式中
bk=mk(1-PD)(PDVk)-1
(26)
(27)
(28)
4)模型概率更新(j=1,2,…,s)
(29)
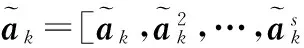
6)状态估计和协方差综合
(30)
(31)
4 仿真结果与分析
所提新算法详细阐明于两个航空机动目标跟踪的情况,传感器采样周期T为1 s,检测概率PD=0.99,门限γ=16,杂波密度λ=0.000 05。
平均均方根误差[17]的计算公式
(32)
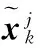
情况1:目标的初始位置在(100,100) km,初始速度为(0,-0.5)km/s,机动目标在1~50 s进行匀速直线运动,在51~70 s以角速度ω=π 40 rad/s匀角速度转弯运动,在71~120 s再进行匀速直线运动,在121~150 s以角速度ω=π/40 rad/s匀角速度转弯运动。仿真结果如图2~图6。
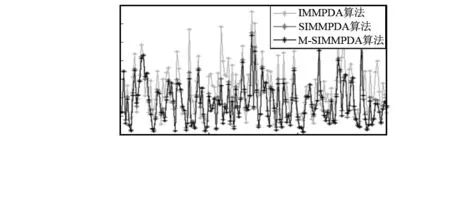
图2 X方向位置均方根误差
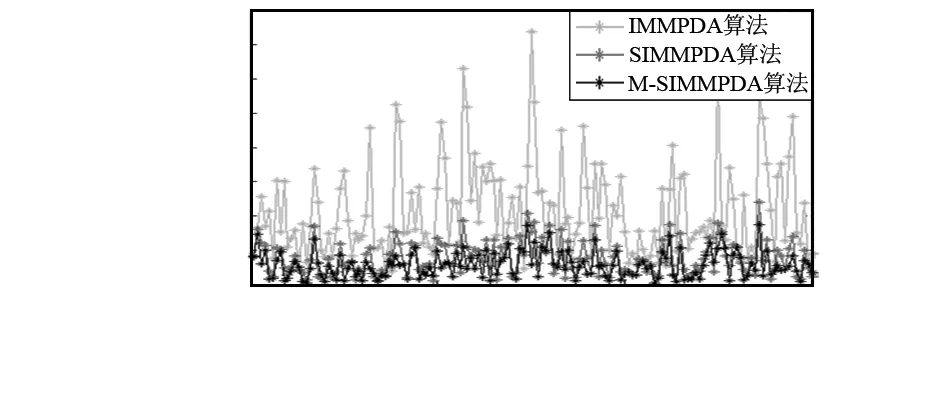
图3 X方向速率均方根误差
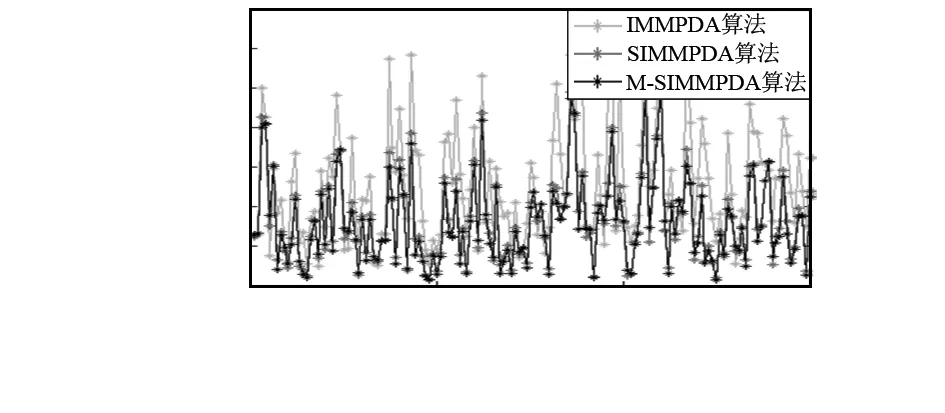
图4 Y方向位置均方根误差
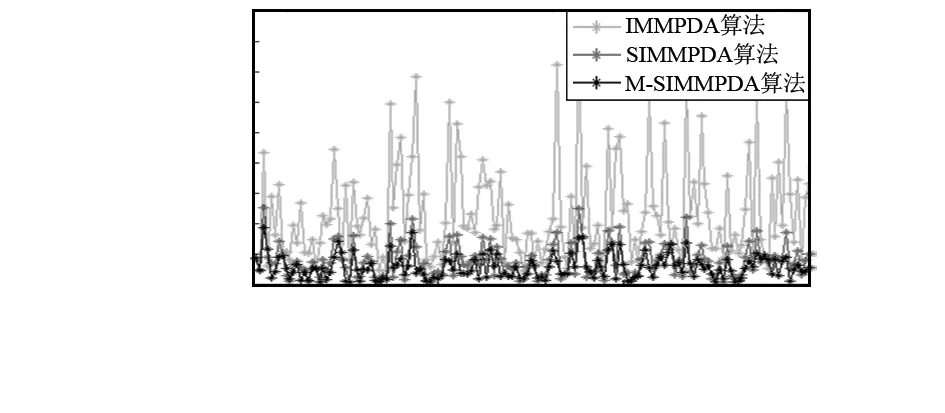
图5 Y方向速率均方根误差
仿真参数设置:采样总时间N=150s,蒙特卡洛运行次数M=1 000,标准的传感器量测噪声方差为r=10km。采用两个不同过程噪声的CV模型,模型1的过程噪声因子q1=0.01,模型2的过程噪声因子q2=50,对应的过程噪声分布矩阵、过程噪声协方差矩阵及状态转移矩阵分别如下
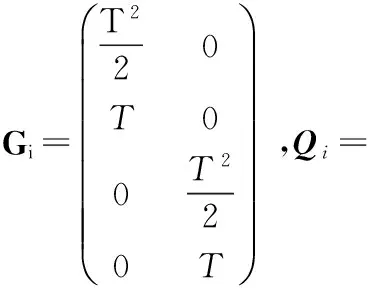
(33)
目标的模型转移概率矩阵及量测矩阵、过程噪声分布矩阵分别如下
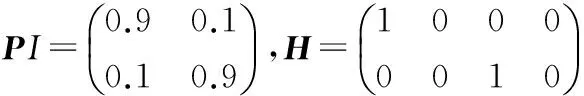
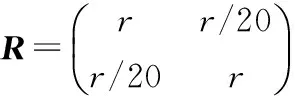
(34)
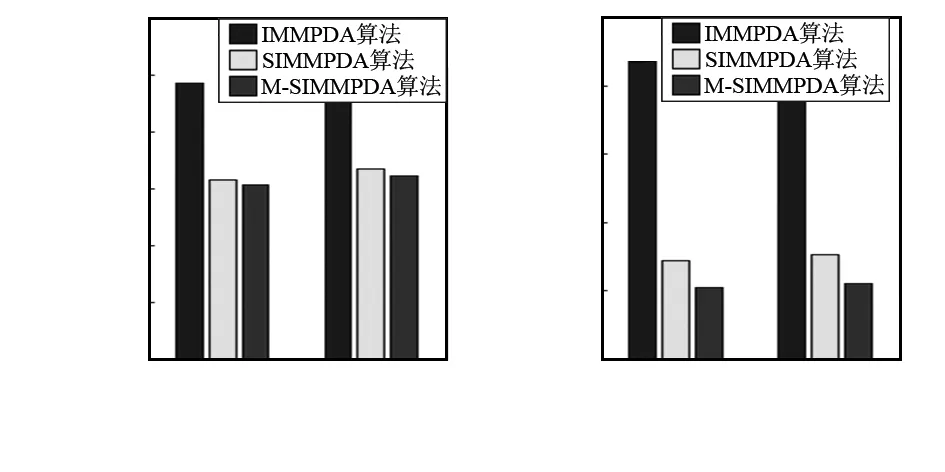
图6 平均均方根误差
情况2:目标的初始位置在(1 000,1 000)km,初始速度为( 1,1 )km/s,机动目标在1~20 s进行匀速直线运动,在21~40 s以角速度ω=-π/40 rad/s匀角速度转弯运动,在41~60 s再进行匀速直线运动,在61~80 s以角速度ω=π/40 rad/s匀角速度转弯运动,最后20 s进行匀速直线运动。仿真结果如图7~图11。
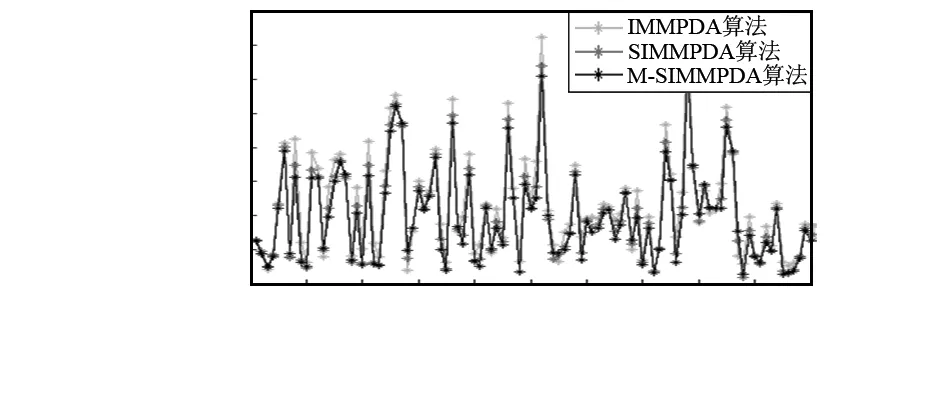
图7 X方向位置均方根误差
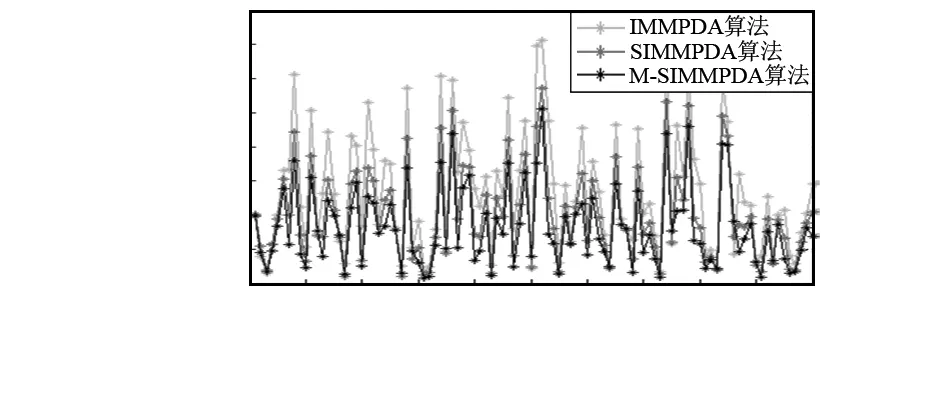
图8 X方向速率均方根误差
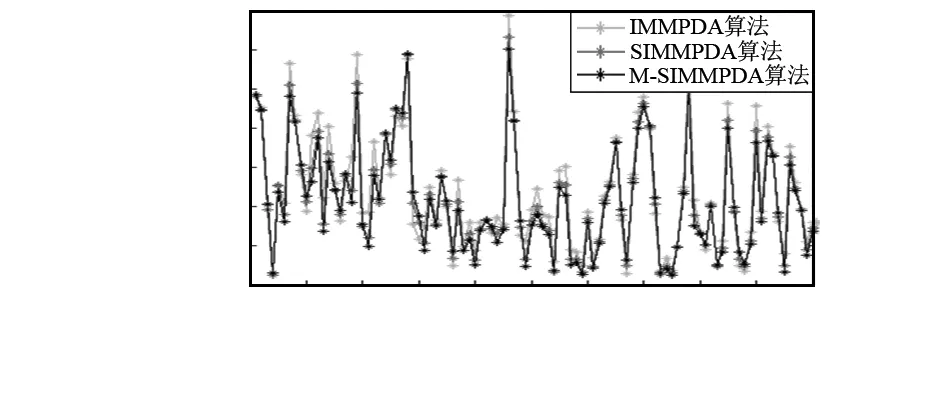
图9 Y方向位置均方根误差
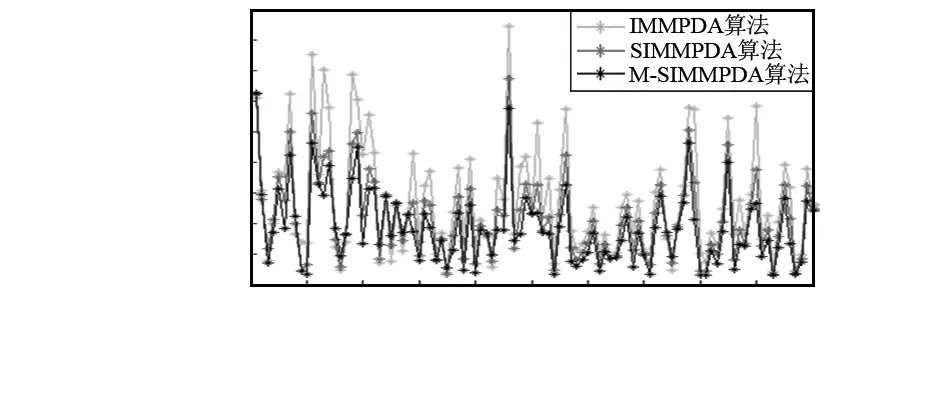
图10 Y方向速率均方根误差
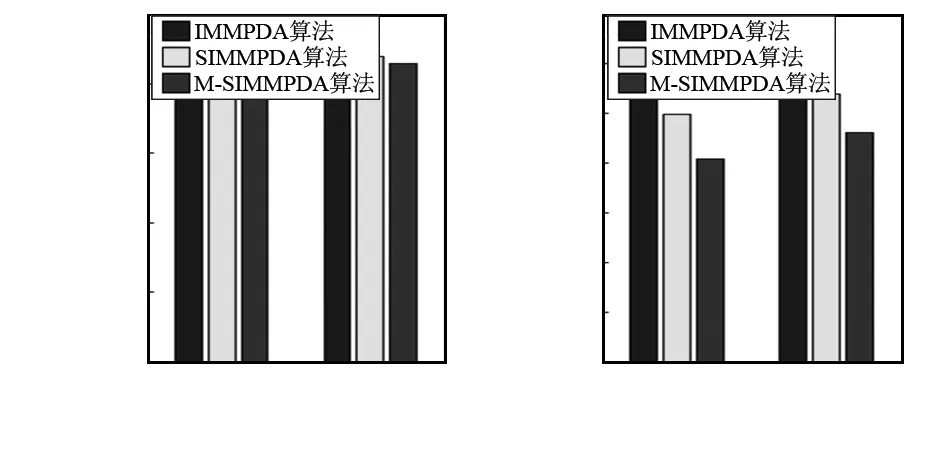
图11 平均均方根误差
仿真参数设置:采样总时间N=100s,蒙特卡洛运行次数M=1 000,标准的传感器量测噪声方差为r=10km,采用三个运动模型:模型1为CV模型,模型2为转角速度ω2<0的CT模型,模型3为转角速度ω3>0的CT模型。模型1的过程噪声因子q1=0.1,模型2,3的过程噪声因子均为qi=50(i=2,3),对应的状态转移矩阵、过程噪声分布矩阵及过程噪声协方差矩阵分别如下

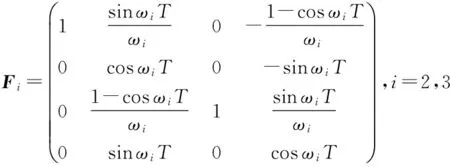
(35)
目标的模型转移概率矩阵及量测矩阵、过程噪声分布矩阵分别为

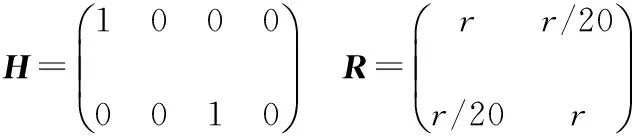
(36)
情况1的仿真结果体现在图2~图6,其图2和图4分别是算法在位置的X方向与Y方向的比较,图3和图5分别是算法在速率的X方向与Y方向的比较,而图6则是算法在X与Y方向分别进行的位置、速率方面的平均均方根误差比较。情况2的仿真结果体现在图7~图11,其图7和图9分别是算法在位置的X方向与Y方向的比较,图8和图10分别是算法在速率的X方向与Y方向的比较,而图11则是算法在X与Y方向分别进行的位置、速率方面的平均均方根误差比较。可以看出,在杂波环境下跟踪机动目标,SIMMPDA算法无论是在位置还是速率方面的均方根误差都小于IMMPDA算法,特别是在速率方面,SIMMPDA算法的性能有着明显的优势。而较之SIMMPDA算法,M-SIMMPDA算法在跟踪性能方面又有着一定的进步。
5 结束语
本文针对实际机动目标跟踪过程中,测量环境并非是“干净”的,存在着许多杂波使测量源不确定,提出了SIMM与PDA的结合算法SIMMPDA算法。进一步考虑杂波的影响导致各时刻匹配运动模型的占优程度不明显的问题,故在算法的每个循环周期对后验模型概率进行修改,形成M-SIMMPDA算法以缓解杂波干扰匹配模型占优程度的问题,进而提高跟踪精度。从仿真结果可以看出:这种新的IMMPDA算法具有更好的跟踪性能,提高了跟踪精确度。
[1]Singer R A,Sea R G.New results in optimizing surveillance system tracking and data correlation performance in dense multitarget environments[J].Automatic Control,1973,18(6):571-582.
[2]Li X R.Tracking in clutter with strongest neighbor measurements I:Theoretical analysis[J].automatic Control,1998,43(11):1560-1578.
[3]Song T L,Lee D G,Ryu J.A probabilistic nearest neighbor filter algorithm for tracking in a clutter environment[J].Signal Process,2005,85(10):2044-2053.
[4]Kirubarajan T,Bar-Shalom Y.Probabilistic data association techniques for target tracking in clutter[C]∥Proceedings of the IEEE,2004:536-557.
[5]Musicki D,Evans R.Joint integrated probabilistic data association:JIPDA[J].Aerospace and Electronic Systems,2004,40(3):1093-1099.
[6]Musicki D,Evans R.Integrated probabilistic data association[J].Automatic Control,1994,39(6):1237-1241.
[7]Bar-Shalom Y,Daum F,Huang J.The probabilistic data association filter[J].Control Systems,2009,29(6):82-100.
[8]Chang K C,Bar-Shalom Y.Joint probabilistic data association for multitarget tracking with possibly unresolved measurements and maneuvers[J].Automatic Control,1984,29(7):585-594.
[9]Chang K C,Chong C Y,Bar-Shalom Y.Joint probabilistic data association in distributed sensor networks[J].Automatic Control,1986,31(10):889-897.
[10] Li Rong X,Vesselin P Jilkov.Survey of maneuvering target tra-cking,part V:Multiple model methods[J].Aerospace and Electronic Systems,2005,41(4):1255-1321.
[11] Kirubarajan T,Bar-Shalom Y.IMMPDA for radar management and tracking benchmark with ECM[J].Aerospace and Electronic Systems,1998,34(4):1115-1134.
[12] Blom H A P,Bloem E A.Probabilistic data association avoiding track coalescence[J].Automatic Control,2000,45(2):247-259.
[13] Fu X,Jia Y,Du J,et al.New interacting multiple model algorithms for the tracking of the manoeuvring target[J].Control Theory and Application,2010,4(10):2184-2194.
[14] Zhou Weidong,Liu Mengmeng.Robust interacting multiple model algorithms based on multi-sensor fusion criteria[J].International Journal of Systems Science,2015,47(1):92-106.
[15] Zhao Shunyi,Huang Biao,Liu Fei.Fault detection and diagnosis of multiple model systems with mismodeled transition probabilities[J].Industrial Electronics,2015,62(8):5063-5071.
[16] Wang Xuezhi,Challa S,Evans R.Gating techniques for maneuvering target tracking in clutter[J].Aerospace and Electronic Systems,2002,38(3):1087-1097.
[17] Zhu Hongyan,Chen Shuo,Han Chongzhao.Fusion of Gaussian mixture models for possible mismatches of sensor model[J].Information fusion,2014,20:203-212.
Novel IMMPDA algorithm with model probability correction*
WANG Mei-jian, WU Xiao-jun
(School of loT Engineering,Jiangnan University,Wuxi 214122,China)
The probability data association(PDA)algorithm is incorporated with scalar interactive multiple model(SIMM) to form SIMMPDA algorithm in order to improve tracking precision of maneuvering target in clutter environment.The PDA algorithm handles data association and measurement uncertainties in clutter environment.The SIMM algorithm deals with the model switching and obtain the optimal state estimations of target in the linear minimum variance sense.In consideration of the problem that the matched model hasn't dominance obvious due to the interference of clutter at each time,so that the model probability of the SIMMPDA algorithm is modified.Thus,a M-SIMMPDA algorithm,which is a SIMMPDA algorithm based on model probability modification is presented.The simulation results show that the tracking precision of the proposed algorithm has been improved to some extent.
maneuvering targets tracking; scalar interactive multiple model(SIMM); probability data association(PDA)
10.13873/J.1000—9787(2016)09—0121—05
2015—10—21
国家自然科学基金资助项目(61373055); 江苏省研究生培养创新工程项目(KYLX—1123)
TP 301.6
A
1000—9787(2016)09—0121—05
王美健(1989-),男,江西吉安人,硕士研究生,研究方向为目标跟踪与信息融合。
