多线圈磁电感应的逆压电式FBG磁场传感器*

黄　俊， 赵成均， 段刘蕊， 赵振刚， 李　川

(昆明理工大学 信息工程及自动化学院,云南 昆明 650504)



多线圈磁电感应的逆压电式FBG磁场传感器*

黄俊， 赵成均， 段刘蕊， 赵振刚， 李川

(昆明理工大学 信息工程及自动化学院,云南 昆明 650504)

将光纤Bragg光栅(FBG)的传感检测技术、直流发电机内部结构的磁电感应原理及压电陶瓷的逆压电效应相结合，研制了一种多线圈磁电感应的逆压电式FBG磁场传感器。设计中采用多线圈磁电感应，输出电流的变化变小，测量均匀磁场的多线圈磁电感应的逆压电式FBG传感器的灵敏度和准确率都能显著提高。对设计的磁场传感器进行了正反行程的重复性测试，并进行对比分析。测试结果表明：该磁场传感器的灵敏度为0.112 8 pm/Gs，迟滞为6.61 %FS，重复性误差为6.29 %FS。

光纤Bragg光栅； 磁电感应； 灵敏度； 迟滞； 重复性误差

0　引　言

相比传统的采用电信号与磁信号进行数据采集的传感器，新型的光纤传感器具有低耗传输、抗腐蚀、抗电磁干扰、抗绝缘等优点，广泛被用于低温、高温、高压、强电磁干扰、强腐蚀等特殊工作环境中。2006年，陈洁等人进行了微系统(MEMS)磁场传感器的研究，根据位移的大小来实现测试磁场大小[1]。2008年，李成章和黄庆安提出了新型梳状谐振磁场传感器[2]。2014年，刘凯和米晓利等人设计了一种用于瞬变电磁法(TEM)高灵敏度感应式磁场传感器[3]。2015年，蒋峰设计了基于钴基非晶带巨磁阻抗(GMI)效应的闭环磁场传感器[4]。

本文研制了一种多线圈磁电感应的逆压电式光纤Bragg光栅(FBG)磁场传感器，利用多线圈切割磁感线，线圈之间的夹角为30°，产生稳定、持续的输出电流，较大提高了磁电感应的逆压电式FBG磁场传感器的测量精度和稳定度。

1　传感器工作原理

利用单片机脉冲宽度调节(PWM)脉宽程序控制驱动电路板，进行转速反馈闭环控制驱动电机达到恒定转速，在驱动电机转速不变的情况下，外部磁场大小发生变化，线圈切割磁场产生的感应电动势发生变化。由于使用单线圈切割磁感线会导致电流变化大，输出不稳定的现象，故使用6个线圈切割磁感线，线圈之间的夹角为30°，从而产生稳定、持续的输出电流。电磁感应现象产生的感应电动势经过电刷和换向器的整流，通过导线将整流后输出电压接在压电陶瓷的垂直轴方向上，作用在压电陶瓷上发生逆压电效应使得粘贴在压电陶瓷上的FBG波长发生移位，根据电磁感应原理、压电陶瓷逆压电效应的数学模型及FBG传感模型，检测获取FBG波长的移位量，进行波长与电压、电压与磁场关系的换算，可以有效地测量外部实际测量磁场的大小。

2　测量模型

由于FBG对温度、应力都会敏感，所以温度和应变力量的变化，都会引起FBG的折射率和对应的栅距发生变化，从而使得对应FBG的反射谱与折射谱都会发生变化。根据光纤耦合的理论数学模型，FBG的中心波长值λB与折射率及周期之间的关系可以表示为

λB=2neffΛ

(1)

式中neff为FBG纤芯有效折射率，Λ为FBG的周期。

不管是对FBG进行压缩或者拉伸作用，都会使得FBG的周期发生变化，光纤的弹光效应也会使其有效折射率随着外加作用力的变化而变化[5]。对式(1)进行微分计算，可以得到外加应力引起FBG的波长移位量ΔλB的表达式为

ΔλB=2neffΔΛ+2ΔneffΛ

(2)

式中Δneff为FBG对应的有效弹光效应，ΔΛ为FBG因外加作用力下的形变量。不同的作用力将会导致Δneff和ΔΛ发生不同的变化。

当FBG发生形变时，它的栅距与折射率也会发生变化，从而引起反射光中心波长的移位量，由式(2)可得

(3)

(4)

(5)

式中ε1为光纤光栅对应的轴向应变量，ν为泊松比，P11和P12为对应的有效弹光系数。其中，对应有效的弹光常数Pe为

(6)

将式(4)、式(5)和式(6)代入到式(2)中，可以得到FBG中心波长的移位量与其所对应的轴向应变量的关系为

(7)

式中λB为FBG的中心波长，ΔλB为波长移位量，Pe=0.22为有效弹光系数，ε为轴向应变量。

轴向应变量ε可表示为如下

(8)

式中l为FBG所在光纤的长度(即表示在压电陶瓷上两个粘接点之间的长度)，Δl为光纤的轴向拉伸。

一个恒定转速下，对应电压输出变化量与磁场大小变化量可以表示为

(9)

由电刷端输出的感应电压加在叠堆型压电陶瓷上，叠堆型压电陶瓷的伸长量Δc与所加电压的关系为

Δc=kΔU

(10)

式中k为所加电压与叠堆型压电陶瓷形变量之间的正比系数。

由于FBG通过两个粘接点粘接在叠堆型压电陶瓷上，压电陶瓷的伸长量Δc与光纤轴向拉伸Δl相等，即

Δc=Δl

(11)

将式(10)和式(11)代入式(8)可以得到光纤轴向应变量ε与加在压电陶瓷上的电压关系

(12)

将式(12)代入式(7)，将电刷端输出的电压引线接在压电陶瓷上，根据压电陶瓷的逆压电效应，得到粘接在压电陶瓷上FBG波长移位量ΔλB与施加在压电陶瓷Z轴上电压ΔU之间的关系为

(13)

将式(9)、式(12)代入式(7)，可以得到FBG的波长移位ΔλB对磁场大小变化ΔB的响应灵敏度为

(14)

通过测量FBG的中心波长的移位量可以计算出实测磁场的大小[6]。

3　传感器的测试系统

对组装后多线圈磁电感应的逆压电式FBG磁场传感器进行测试，测试系统如图1所示。

当测试系统中基于逆压电效应的FBG磁场传感器感知到磁场的变化时，根据电磁感应原理，会将磁场的变化转换到相应电流的变化，压电陶瓷两端的电压随之变化，从而引起Bragg光栅中心波长的位移量变化。通过FBG解调仪解调之后，可以将检测到的光信号解调成相应的电信号，并将数据传送至计算机上位机软件。计算机通过检测软件与自身的处理，解调到与磁场大小相对应的波长值，通过显示屏以数字形式显示。

4　磁场传感器的性能指标分析

1)灵敏度：单次正或反行程过程中输出FBG中心波长的移位量与输入磁场大小的变化量之比[7]

s=Δλ/ΔB

(15)

式中Δλ为单次正或反实验过程中FBG中心波长的移位

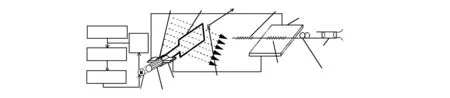
图1　多线圈磁电感应的逆压电式FBG磁场传感器测试系统图

量，ΔB为单次正或反行程实验中磁场大小的变化量。

三次正反行程实验过程中，磁电感应的逆压电式FBG磁场传感器的灵敏度，如表1所示。

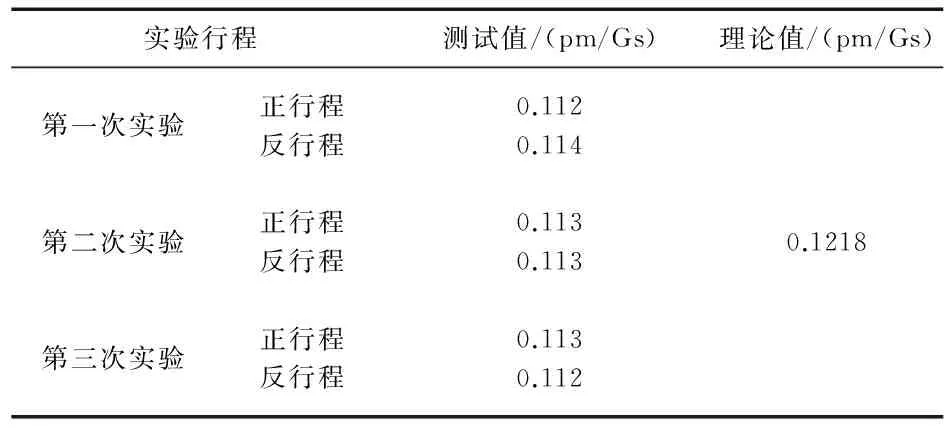
表1　三次正反行程实验中FBG磁场传感器的灵敏度

通过对表1的实验进行数据处理分析，对三次正反行程实验中所得灵敏度求算术平均值，可以得到传感器测试系统的灵敏度为：在正行程实验中，灵敏度为0.112 7 pm/Gs，在反行程实验中，灵敏度为0.113 pm/Gs，对正反行程实验求平均值，最终可得磁场传感器的灵敏度为0.112 8 pm/Gs。

2)迟滞：磁场传感器在进行正反行程实验过程中，磁场上升与波长位移值的关系曲线和磁场下降与波长位移值的关系曲线之间的偏离程度[8]。对于本文设计的磁场传感器而言，其迟滞可以表示为正反行程实验过程中，对应的最大波长偏差值与满量程输出波长移位量之比，对应迟滞的关系式可以表示为

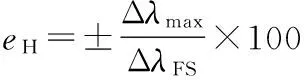
(16)

式中Δλmax为进行正反行程实验过程中的FBG中心波长的最大偏差值，ΔλFS为FBG满量程输出的中心波长的移位值。

在三次正反行程实验过程中，可以找出每个相同磁场强度下，对应三次正反行程实验的FBG波长偏差的最大值与正反实验平均满量程输出波长移位量的数据参数，如表2所示。

根据式(16)计算可得，第一次实验系统的迟滞为7.14 %FS，第二次实验系统的迟滞为7.14 %FS ，第三次试

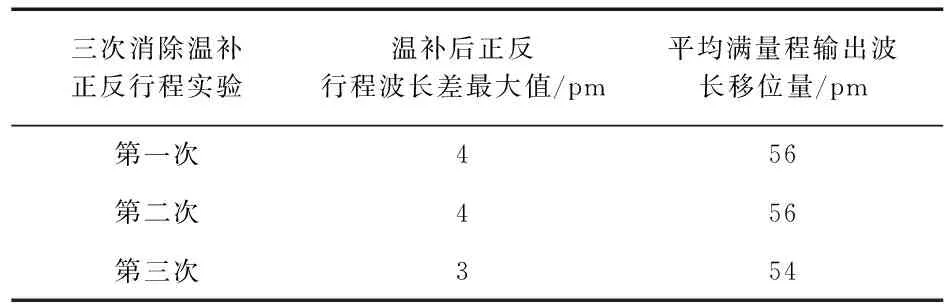
表2　三次实验中消除温度补偿后的正反行程波长差的最大值

验系统的迟滞为5.55 %FS ，对以上三次实验的迟滞求算术平均值可得，FBG磁场传感器的迟滞为6.61 %FS。

3)重复性误差[9]：对该磁场传感器而言，其重复性误差就是直接反应了在同样的环境、实验设备等实验条件下进行重复性实验时，FBG中心波长的移位量能否保持一致的性能，可以表示为

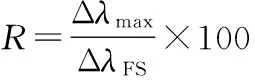
(17)

式中Δλmax为三次正反行程实验中FBG中心波长之间的最大偏差值，ΔλFS为FBG满量程输出的中心波长的移位量。根据式(17)对磁场传感器进行分析，得到该磁场传感器试验的最大重复性误差为：正行程实验的重复性误差为5.45 %FS，反行程试验的重复性误差为7.14 %FS，可得该磁场传感器试验的平均重复性误差为6.29 %FS。

5　结　论

本文结合FBG的传感检测技术、直流发电机的磁电感应原理与压电陶瓷敏感元件的特性，研制了一种多线圈磁电感应的电致伸缩式FBG磁场传感器。多线圈磁电感应有效地提高了FBG磁场传感器的测量精度和稳定度，并搭建了多线圈磁电感应的逆压电式FBG传感器的测试平台，对该磁场传感器的正反行程进行重复性测试，通过对磁场传感器测试数据的处理与分析，可以计算出磁场传感器的相关静态性能指标。实验表明：该磁场传感器的灵敏度为0.112 8 pm/Gs，迟滞为6.61 %FS，重复性误差为6.29 %FS，具备低耗传输、抗腐蚀、抗电磁干扰、强绝缘性等优点，可以适用于核工业、石油、冶金、化工等特殊的工业环境中。

[1]陈洁,黄庆安,秦明.MEMS磁场传感器的研究进展[J].电子器件,2006(4):1384-1388.

[2]李成章,黄庆安.梳状谐振式磁场传感器设计[J].微纳电子技术,2007(Z1):279-281.

[3]刘凯,米晓利,朱万华,等.一种用于TEM高灵敏度感应式磁场传感器设计[J].地球物理学报,2014(10):3485-3492.

[4]蒋峰.基于钴基非晶带GMI效应的闭环磁场传感器设计[J].磁性材料及器件,2015(1):64-68.

[5]姜德生，何伟．光纤光栅传感器的应用概况[J]．光电子·激光，2002，13(4)：420-430.

[6]李川.光纤传感器技术[M].北京：科学出版社，2012:344-355.

[7]Putnam M A,Dennis M L,Duling I N,et al.Broadband square-pulse operation of a passively mode-locked fiber laser for fiber Bragg grating interrogation[J].Optics Letters,1998,23:138-140.

[8]Measures R M,Structural monitoring with fiber optic technolo-gy[J].Califiornia:Academic Press,USA,2001.

[9]范伟，余晓芬.压电陶瓷驱动器蠕变特性的研究[J].仪器仪表学报，2006，27(11)：1383-1386.

Multi-coil magnetoelectric induction of inverse piezoelectric FBG magnetic field sensors*

HUANG Jun, ZHAO Cheng-jun, DUAN Liu-rui, ZHAO Zhen-gang, LI Chuan

(School of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650504,China )

Combine optical fiber Bragg grating(FBG)sensing technology,magnetoelectric effect principle of internal structure of DC generator and inverse piezoelectric effect of piezoelectric ceramic,develop an inverse piezoelectric FBG magnetic field sensors based on multi-coil magnetoelectric induction.The design uses multi-coil magnetoelectric induction,change of output current is getting smaller, sensitivity and accuracy of the inverse piezoelectric FBG sensors can be improved significantly.Repeatability test of forword and reverse stroke of magneticfield sensors is carried out,and comparative analysis on test data is carried out.Test results show that sensitivity of the magnetic field sensor is 0.112 8 pm/Gs,hysteresis is 6.61 % FS,repeatability error is 6.29 % FS.

fiber Bragg grating(FBG); magnetoelectric induction; sensitivity; hysteresis; repeatability error

10.13873/J.1000—9787(2016)09—0098—03

2015—11—23

国家自然科学基金资助项目(51567013)

TP 212.1

A

1000—9787(2016)09—0098—03

黄俊(1991-)，女，湖南益阳人，硕士研究生，研究方向为传感器技术。