激光三角位移传感器定位算法优化设计*

陈家兴， 陶　卫， 杨红伟， 曾新贵， 张正琦， 赵　辉

(上海交通大学 电子信息与电气工程学院，上海 200240)



设计与制造

激光三角位移传感器定位算法优化设计*

陈家兴， 陶卫， 杨红伟， 曾新贵， 张正琦， 赵辉

(上海交通大学 电子信息与电气工程学院，上海 200240)

采用激光三角测距原理设计并制作了高集成度的激光三角位移传感器测头LDSP—100。第一版机型的软件算法基于曲线拟合中的多项式拟合和高斯拟合，进行光斑定位。由于一体化设计对光斑定位稳定性要求极高，单纯的拟合算法定位无法满足。经进一步优化设计，实现了基于平方加权灰度质心的分段平均算法。实验、对比和分析表明：优化后的基于平方加权灰度质心的分段平均算法，重复性误差达到±0.003 7 mm(100 mm量程)，即±0.003 7 %F.S.，高于基于灰度质心的分段平均算法60.4 %；高于高斯拟合算法22.9 %。

激光三角测量； 重复性精度； 高斯拟合法； 灰度质心； 平方加权灰度质心； 分段平均

0　引　言

在激光三角位移传感器的发展过程中，高集成度的一体化测头越发受到青睐。在传感器集成度逐步提高的过程中，光学、机械、电子等硬件规模的缩小，会引入影响传感器性能的不稳定因素。经过调测，在硬件系统相对成熟的前提下，优化软件算法，成为大幅度提高传感器精度和稳定性的首要任务。

在一体化的激光三角测距原理设计中，激光光斑成像波形畸变增大，传统的高斯拟合和灰度质心算法均无法满足定位的重复性要求。基于平方加权灰度质心的分段平均算法，对消除随机误差，滤除波形波动均有较好效果，达到了目前最好的重复性精度。

1　激光三角测距原理

激光三角测距原理是激光测量的典型应用之一[1]。激光三角原理如图1、图2所示。激光三角测量结构分为直射式与斜射式两种，受传感器体积因素限制，本文在研制过程中采用的是直射式结构。

激光光源发出激光，经过发射镜(组)进行准直和聚焦，投射到被测物表面形成光斑直径小于1 mm的点状光斑，光斑由目标物漫反射后由接收透镜(组)聚焦，成像于位置器件表面。目标物移动距离E与成像距离s之间的关系如式(1)所示[3]

(1)

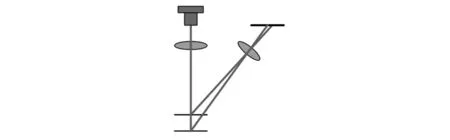
图1　激光三角测距(直射式)原理

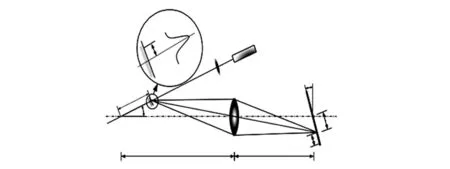
图2　激光三角测距几何关系

2　激光三角测距原理的光斑定位问题

现行激光三角位移传感器[3]，普遍采用外形小巧、价格低廉的半导体激光二极管作为激光光源。本文采用光源为650 nm激光二极管，位置器件为东芝TCD2566BFG型CCD。但激光二极管光束发散角较大，由其本身的物理特性决定光斑会有径向跳动。由光斑质量分析仪测得，跳动范围为±0.003 6 rad。

在理想情况下，激光光斑能量分布应接近高斯分布，其光斑能量中心即为波形峰值对应位置。但实际研制过程中，得到的波形如图3。在0～5 200像素范围内的波形，由主峰与随机噪声叠加而成；由于CCD双通道输出，两个通道(奇偶像素)间存在细微差异，也造成了主峰的不连续，图4为主峰波形放大，左侧阴影处实际为奇偶像素的幅值波动。

对于主峰的处理，主要面临两个问题：1)主峰不完全对称，峰顶处接近饱和状态，因此，不能依靠单纯搜索最大幅值点定位光斑中心；2)激光二极管稳定性差[4]，光斑位置会有一定的随机波动，且电路波动会引入随机噪声。

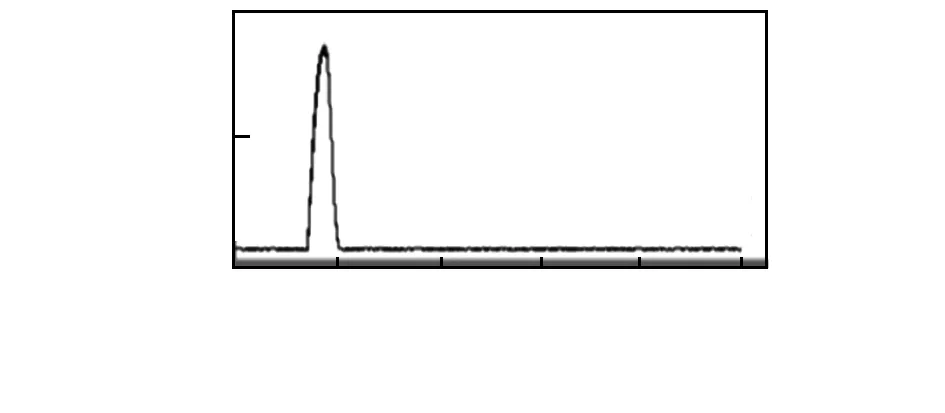
图3　CCD原始数据波形

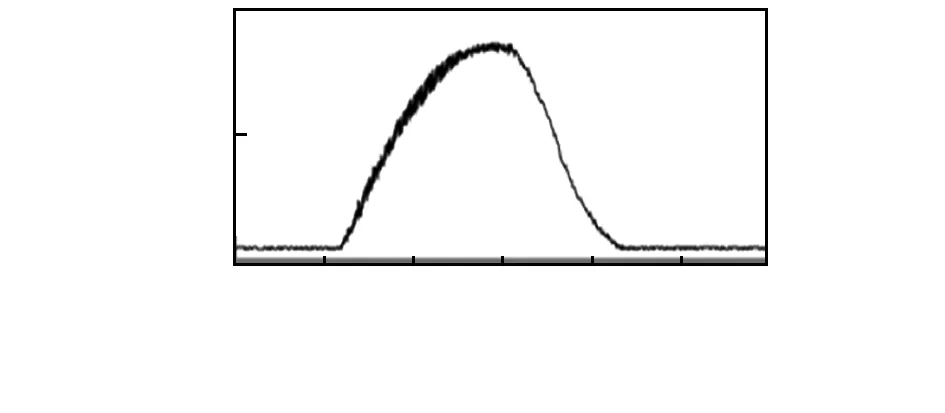
图4　CCD波形主峰放大

针对以上问题，激光三角测距中的光斑定位算法除了能定位光斑外，还要对波形位置的随机波动具有一定的滤波作用，以保证测量结果的重复性精度。

在首批样机LDSP—100中，高斯拟合方法得到采用。为了进一步优化算法，提高光斑定位的重复性精度，本文设计并验证了基于灰度质心、基于平方加权灰度质心的分段平均算法(简称分段平均法)，并与原有拟合方法做比较，确定了目前最优算法：基于平方加权灰度质心的分段平均算法。

3　光斑定位算法原理与软件结构

3.1表征光斑位置特征量的定性分析

在理想状态下，激光光斑能量分布为高斯分布。因此，之前的定位算法，采用了高斯拟合法，并以拟合后高斯曲线的对称轴像素坐标作为当前光斑的位置量。

深入分析发现高斯拟合法存在两个不足：1)由于出射镜组和接收镜组引起的畸变和位置器件CCD的位姿因素影响，光斑成像有倾斜和拉抻情况，并不完全符合高斯曲线的对称性；2)不对称的光斑曲线，其位置应由峰顶位置(光斑最亮点)和能量中心(灰度质心)共同表征。因此，改进的定位算法，综合考虑了灰度质心与曲线峰顶的共同作用。

3.2基于平方加权灰度质心的分段平均算法[5]

分段平均算法软件流程图如图5。

3.2.1主峰定位预处理

如前所述，即使光斑质量达到最佳状态，由于干涉和电路信号稳定性等因素，得到的光斑波形仍然包含一些小尖峰和随机噪声。为滤除这种干扰，本文首先对原始波形进行粗定位[6]。

本文采用CCD的黑白模式，并在设计中留有量程余量，因此，每帧数据包含5 200个像素的信息(共5 340个像素，保留140个边缘像素)。粗定位过程会对5 200个像素进行遍历，寻找最大值Valmax及其像素位置ValPosmax。截取幅值超过Valmax/2的像素作为主峰，截取后波形如图6。其左右边界分别记录为leftPos和rightPos。

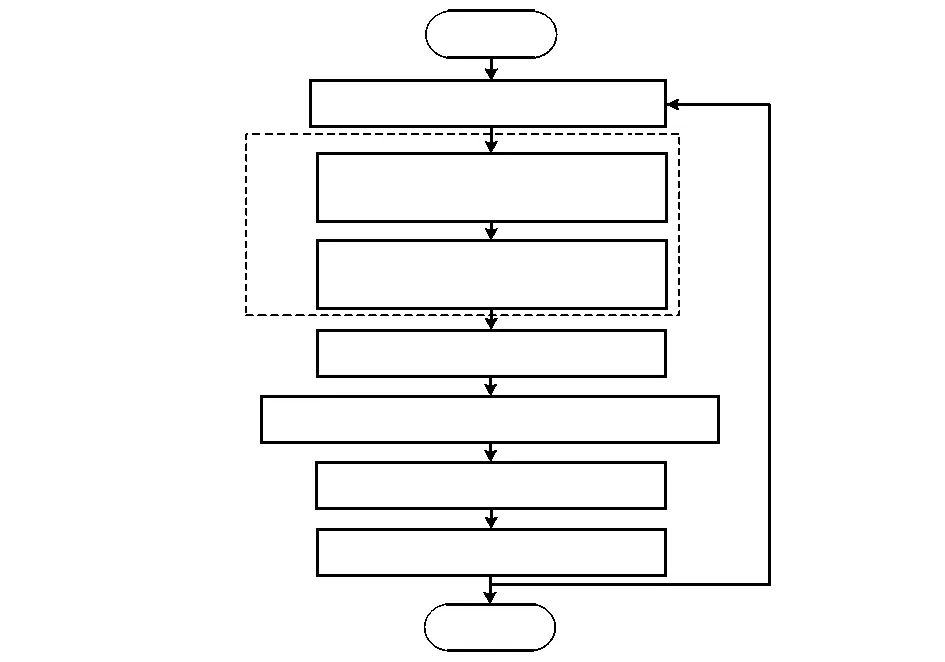
图5　分段平均算法软件框图

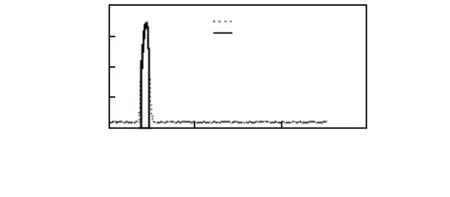
图6　CCD原始数据粗定位波形

由此可见，粗定位优点如下：1)滤除主峰以外的次峰及主峰边缘处的影响；2)大大减少数据量，提高处理效率。

3.2.2灰度质心数学原理

灰度质心又称重心，是图像处理中常用的一种方法,该算法数学表达式为

(2)

式中xi为像素值，yi为对应的信号幅值。实际运算式为

(3)

式中M为截取宽度(M=rightPos-leftPos)，K为截取波形初始位置(K=leftPos)。

3.2.3平方加权灰度质心数学原理

平方加权灰度质心原理中采用灰度(幅值)的平方代替灰度值，提高了峰值附近权重。相比之下，会降低随机噪声的比例。后述实验也证明，基于平方加权灰度质心的算法重复性精度高于基于灰度质心的算法，即

(4)

同理，可以得到粗定位截取波形的计算式

(5)

3.2.4分段平均算法

基于前述的数学原理，单纯的全波形灰度质心，只包含了光斑波形的能量中心信息， 而回避了光斑最亮点(峰值)的意义。因此，本文设计了全波形的分段平均算法。

针对(粗定位后)波形幅值，按5 %递减分段，将全波形(Valmax/2～Valmax)分为10段。对每一段数据分别求其平方加权灰度质心，最后对此10个质心再求取加权平均，即得波形的最终位置。

这种基于平方加权灰度质心的分段平均算法，其优势在于既保留了能量中心的信息，又通过各段权重的调整保留了光斑最亮点信息和波形最稳定区间的信息，从而提高了光斑定位的稳定性和客观性。

3.3高斯拟合法相关理论[7]

激光二极管所发光束接近高斯光束，其能量分布近似于高斯分布。因此，采用高斯曲线近似描述光斑曲线，是激光三角测量中一种比较经典和常用的处理方法。

高斯分布表达式

(6)

式中y0为随机噪声均值，x0为所求波形的中心位置。根据波形数据，选取合适参数近似描述光斑曲线，再计算高斯波形对称轴坐标。高斯拟合结果如图7。

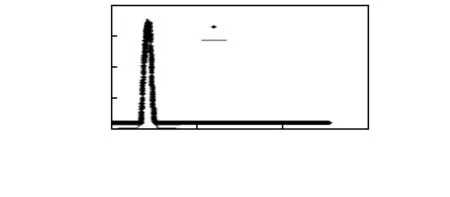
图7　高斯拟合结果

4　算法处理结果与精度分析

4.1验证实验

4.1.1实验装置

设计搭建了数据采集和重复性精度测量系统。

实验样机：实验室自主开发的一体化激光位移传感器测头，内部型号LTDS—100，量程100 mm，测量范围50～150 mm；以光学抗振平台与丝杠导轨为搭载平台；基准仪器为雷尼绍XL—80双频激光干涉仪；用PC采集与保存数据。

系统结构示意图如图8。实验样机LTDS—100固定在导轨首端；被测物(陶瓷量块)与双频激光干涉仪的光学组件固定在导轨的移动平台；双频激光干涉仪固定于导轨尾端。整个光路调节在同一直线上。

4.1.2数据采集方法

以双频激光干涉仪读数为基准，监测被测物移动距离和静止时系统的稳定性。充分预热使机器达到稳定工作状态。移动被测物，分别停止在量程的近端(55 mm)、零点(100 mm)、远端(145 mm)附近，待双频激光干涉仪读数稳定时，对这三个位置采集CCD原始数据。为保证重复性实验的有效性，实验中LTDS—100只进行采集，并通过USB传输到上位机进行保存。测头本身对数据不做任何处理。这样，采样速度可达900 Hz(帧速)，可在1 s内完成每个位置200帧数据采集，既保证系统短时间内免受外界干扰，又可以保证数据量，增加可信度。采集结束后，对保存的原始数据进行算法处理。处理工具为Matlab，算法为测头内部集成算法的移植。

这种数据离线的处理方法，可以保证采集过程不受干扰，且保留了原始数据，方便进行复杂计算与分析。

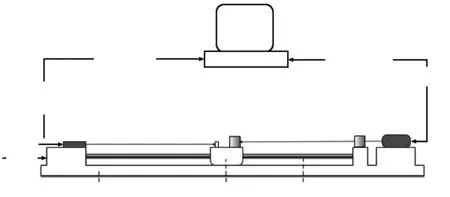
图8　测试系统示意图

4.2数据处理结果对比分析

数据处理[8]过程如下：1)对原始数据，分别使用分段平均算法和原有高斯拟合算法进行计算，换算得到位移值；2)对位移值求平均，作为标准值；3)将每组位移值与本组标准值做差，得到稳定性误差；4)对c中所得的稳定性误差进行极差、标准差分析，并做误差曲线，比较不同算法的稳定性结果。

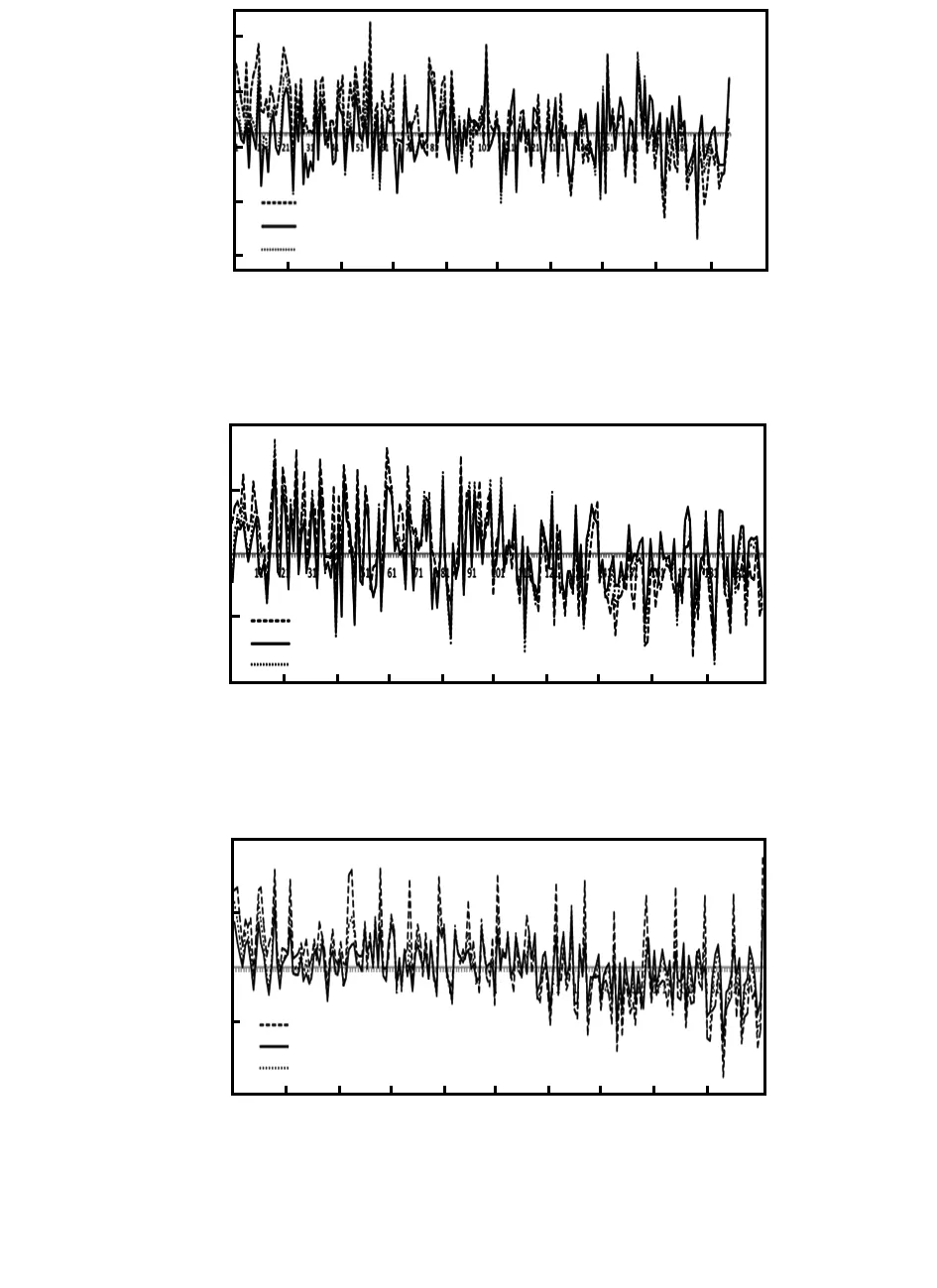
图9　重复性误差对比曲线

经实验检测和数据分析，得到计算结果误差分析表与不同算法误差曲线，见表1、图9。

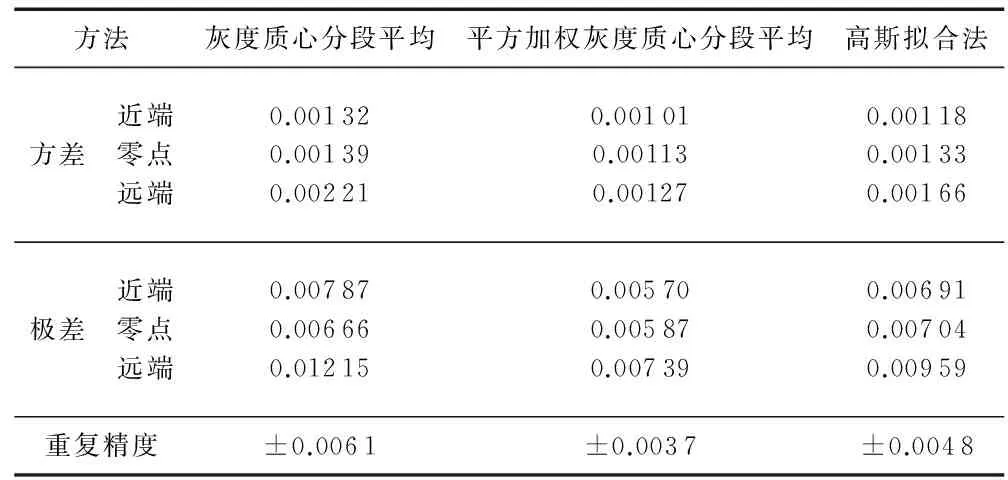
表1　计算结果误差分析

5　结束语

针对本文设计的量程为100 mm的一体化激光三角位移传感器LDSP—100，为解决其稳定性误差问题，提高重复性精度，采取基于平方加权灰度质心的分段平均算法进行定位和运算。

该算法不仅保留了实际光斑最亮点的位置信息，也综合了光斑能量中心的特征，提高了光斑定位的稳定性和客观性。此算法较高斯拟合算法相比，重复性精度显著提高，达到±0.003 7 mm，即±0.003 7 %F.S.。

[1]Sirohi R S,Chau F S.Optical methods of measurement[M].New York:CRC Press.1999:56-70.

[2]Lombardo V,Marzulli T,Pappalettere C,et al.A time-of-scan laser triangulation technique for distance measurements[J].Optics and Lasers in Engineering,2003,39(2):247-254.

[3]Cigada A,Manzoni F,Manzoni S,et al.Laser-triangulation device for in-line measurement of road texture at medium and high speed[J].Mechanical Systems and Signal Processing,2010,24(7):2225-2234.

[4]胥绍禹.半导体激光器驱动电路的制作[J].集成电路应用,2000(5):38-40.

[5]孙军利,赵辉,陶卫.具有亚像素级定位精度的激光三角测距新算法[J].激光杂志,2006,27(4):22-23.

[6]刘立波,赵辉,张海波.激光三角测距中光斑细分定位方法研究[J].计算机测量与控制，2008，16(10):1396-1398.

[7]金文燕,赵辉,陶卫.激光三角测距传感器建模及参数优化研究[J].传感技术学报,2006,19(4):1090-1093.

[8]黄战华,蔡怀宇,李贺桥,等.三角法激光测量系统的误差分析及消除方法[J].光电工程,2002,29(3):58-61.

陈家兴(1991- )，男，满族，辽宁锦州人，硕士研究生，研究方向为光电检测与现代传感器。

陶卫，通讯作者，E—mail：taowei@sjtu.edu.cn。

Optimized design of locating algorithm for laser triangulation displacement sensor*

CHEN Jia-xing, TAO Wei, YANG Hong-wei, ZENG Xin-gui, ZHANG Zheng-qi, ZHAO Hui

(School of Electronic Information and Electrical Engineering,Shanghai Jiaotong University,Shanghai 200240,China)

Displacement sensors based on laser triangulation ranging principle are widely used because of advantages of small volume and high precision.Highly integrated laser triangulation displacement sensor named LDSP—100 is developed.The algorithm utilizes in the first vision of LDSP—100 is based on polynomial fitting and Gauss fitting method,light spot localization is carried out,but stabilization is highly required in integrated design,single fitting method can not meets the needs.An optimized algorithm called segment average algorithm based on square weighted gray centroid is designed and realized.And this is proved to be better than Gauss fitting method.According to a series of experiment and analysis,it is found that the repeatability precision can achieve ±0.0037 mm,which equals to ±0.003 7 %F.S.with segment average algorithm based on square weighted gray centroid.It is 60.4 % higher than gray centroid segment average algorithm and 22.9 % higher than Gauss fitting algorithm.

laser triangulation measurement; repeatability precision; Gauss fitting method; grey centroid; square weighted grey centroid; segment average

10.13873/J.1000—9787(2016)09—0062—04

2015—11—03

上海市闵行区科委产学研项目(2014MH116)

TH 744

A

1000—9787(2016)09—0062—04