基于模糊PI控制的PWM整流器设计

邵泽龙， 石明全， 韩震峰(中国科学院重庆绿色智能技术研究院，重庆400714)

基于模糊PI控制的PWM整流器设计

邵泽龙， 石明全， 韩震峰
(中国科学院重庆绿色智能技术研究院，重庆400714)

针对双闭环矢量控制的三相电压型PWM整流器难以用准确的数学模型描述、以及通过其简化的数学模型求得的PI参数需要实验整定的问题，提出了基于模糊PI控制器的新型智能化控制方法。与传统的PI控制方法相比，该方法不仅实现了PI参数的自整定，还使系统具有更好的响应性能、更高的稳定性及鲁棒性。利用Matlab/Simulink工具箱建立了基于模糊PI控制器的整流器仿真模型，并通过仿真实例对此设计方法进行了实验验证。

PWM整流器；双闭环控制；模糊PI控制；参数整定；仿真

三相电压型PWM整流器具有功率因数高、电流畸变小、能量双向流动等优点，被广泛应用于电机驱动、蓄电池充放电和风力发电等场合，其控制方法多种多样，有电压控制、电流控制、功率控制等。在各种控制方式中，以电压反馈作外环加上电流反馈作内环的双闭环控制结构最为普遍[1]。此种控制方案具有控制结构较为简单、动态响应快、控制精度高、对网侧参数不敏感等优点[2]。但是，整流器的内部电压、电流转换过程难以用精确的数学模型表达。而一些文献通过整流器的简化数学模型得到的理论PI参数值在实际应用中并不能得到理想的实验结果[3]。

模糊控制是一种新型智能控制策略，它不要求精确掌握被控对象的数学模型，而是根据实验人员的操作经验形成控制规则，在线实时调节控制对象以达到良好的输出响应[4]，不仅具有常规PI控制精度高、速度快的特点，也具有适应性强、鲁棒性高的特点。

本文简要介绍了三相电压型PWM整流器的工作原理，概括了控制器PI参数的理论计算方法，结合模糊控制与常规PI控制建立了基于模糊PI控制的整流器仿真模型，通过仿真实例验证了该设计方法的正确性和有效性。

1 PWM整流器的原理与设计

1.1整流器的电路结构和控制原理

本文所研究的PWM整流器电路结构如图1所示，其工作原理为通过对6个开关管进行控制，改变Ua、Ub、Uc的波形和相位，从而改变输入电流的相位，以达到高功率因数整流的目的[5]。

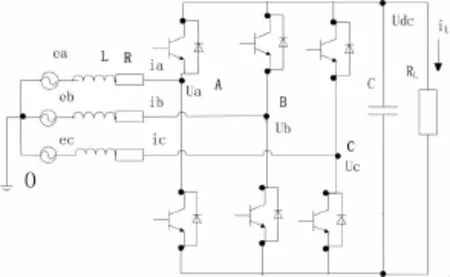
图1　PWM整流器主电路

由图1所示的电路结构，建立采用开关函数描述的数学模型如式(1)所示[6]。此模型中，由于交流侧电量为时变交流量，控制系统的设计十分困难。若将三相对称静止坐标系(a、b、c)通过PARK变换到同步旋转坐标系(d、q)中，则原来的交流正弦变量变为直流变量。

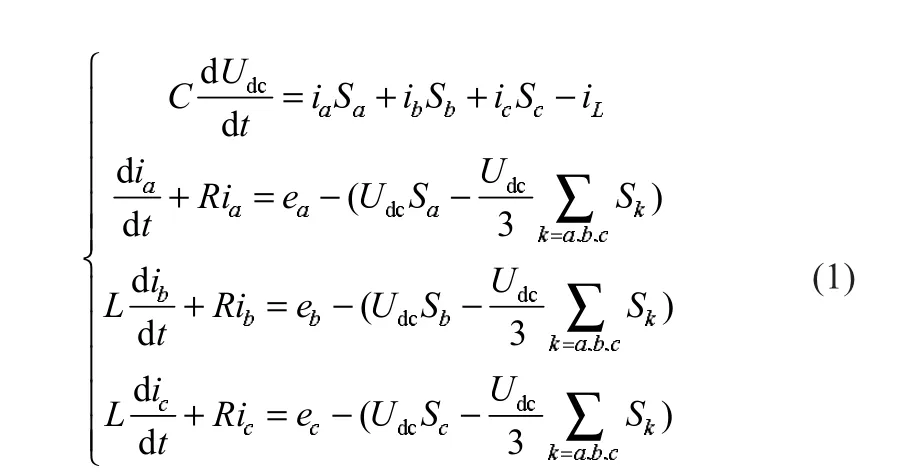
式中：Sa、Sb、Sc为桥臂上通下断或上断下通的二值逻辑开关函数。

通过PARK变换后系统d、q轴变量相互耦合，对控制器的设计产生不利影响。此时若采用前馈解耦控制策略，urd、urq的控制方程变为：

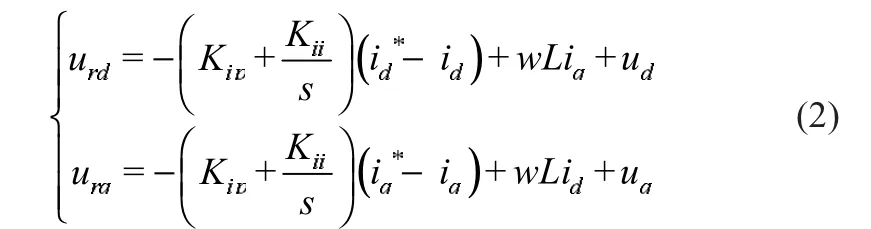
式中：id*、iq*为id、iq的电流指令值；urd、urq为交流侧电压矢量的d、q轴分量。

如此，PWM整流器电流内环实现了解耦控制，再加上外环的电压控制就构成双闭环矢量控制的整流器系统，其控制原理如图2所示。

图2　整流器控制原理

1.2PI参数的理论选取

双闭环整流器含有3个PI控制器，这3个控制器的参数需要协调配合才能获得良好的控制效果。其中，电流环d、q轴的两个PI调节器参数相同。因此，实际工程应用只需要确定两组PI参数，即电流环的Kip、Kii和电压环的Kup、Kui。

PI参数的选择方法多种多样。文献[2]参照双闭环调速系统的设计[7]，电流内环采用了典型Ⅰ型系统进行设计，电压外环采用了典型Ⅱ型系统进行设计。文献[8]则根据“ITAE性能最佳准则”给出了能够满足系统电流内环及电压外环响应特性的PI参数设计方法。文献[9]则基于d、q坐标系的线性解耦小信号动态模型，给出了能兼顾系统稳定性和抗扰动性的PI参数设计方法。其参数取值如式(3)所示。

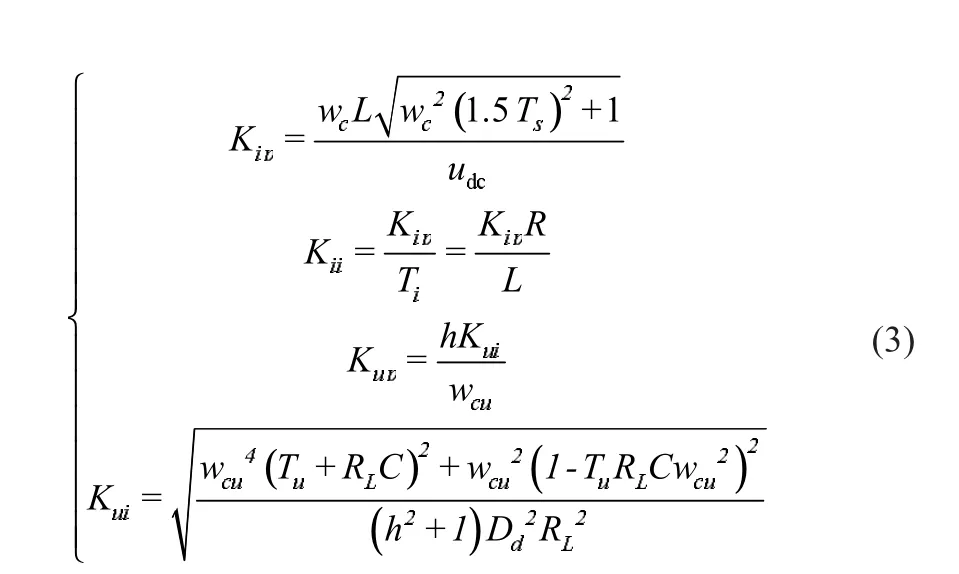
式中：ωc为电流内环的截止频率；ωcu为电压外环的截止频率；Ts为PWM的开关周期；Dd为电压系数，其值为Ed/Udc；Tu为电压外环的等效时间常数，其值可以通过下式求得：

式中：Qu为电压外环的品质因数；h为电压外环中频带宽系数。

这些理论参数的计算方法虽然折中考虑了系统的动态和稳态性能，理论上已经十分理想，但是，理论推导过程中所采用的数学模型与系统实际运行情况存在较大差距，理想的PI参数值仍然需要通过实验整定得出。而重复不断的参数实验整定过程会消耗研究人员极大的精力和时间，而采用基于模糊PI控制器的整流器可以使得系统根据操作人员的经验，自动在线整定PI参数。从而，给予了实验人员极大的便利。

2 模糊PI控制器的设计

2.1模糊PI控制器的结构

传统的PI调节器虽然动态响应良好，但对于整流器这一多变量、非线性系统，很难获得理想的控制效果[10]。模糊PI控制器是在传统PI控制器的基础上，应用模糊集合理论建立PI参数Kp、Ki与偏差e、偏差变化率ec之间的函数关系。并根据e 和ec的不同，实时改变PI参数的控制系统，其原理如图3所示。

图3　模糊PI控制原理

2.2模糊PI控制器的仿真模型

利用Matlab/Simulink工具箱，结合常规PI控制算法与模糊控制模块[11]，建立了模糊PI控制器的仿真模型，如图4所示。其中，偏差e和偏差变化率ec需要经过数学运算后量化到模糊语言论域上，才能输入到模糊控制模块。PI参数Kp、Ki的取值也需要根据工程实验人员的操作经验，将模糊控制模块的输出经过数学运算后得到。

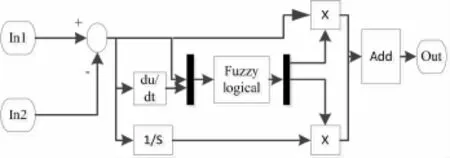
图4　模糊PI控制器

3 PWM整流器仿真实验

3.1PWM整流器仿真模型

Matlab是电力电子仿真的理想工具，不仅关注器件的外特性，且易于和控制系统相连接[12]。三相电压整流器的仿真模型如图5所示，主要由主电路模块、测量模块和控制模块三部分组成。其主电路模块由交流电源、三相整流桥、直流负载、电阻电感等基础电路元件组成；测量模块主要由示波器和数学运算模块组成；而其控制模块比较复杂，涉及到电压和电流的双闭环反馈控制。

图5　整流器仿真模型

为了简化其控制模块的设计，采用Simulink支持的S-函数，用C语言编写需要的函数模块[13]。S-函数即system function，其采用特定的调用语法，使得用户编写的运算模块可以与Simulink解法器相连接，从而广泛应用于连续、离散、混合等各类控制系统。其控制模块如图6所示。

3.2PWM整流器仿真实例

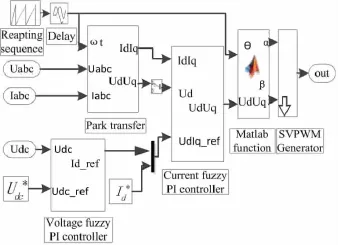
图6　控制器仿真模型

本文通过一个工程应用实例来简要说明三相电压型PWM整流器的设计过程，并通过此实例分别应用常规PI控制器和模糊PI控制器时系统响应的不同，来验证模糊PI控制器的性能。

算例为：三相交流电输入em=311 V，f=50 Hz；直流侧负载电阻RL=20 Ω；开关管的开关频率fs=10 kHz。调制方法采用SVPWM方式。

根据式 (3)，可以求得：Kup=0.5，Kui=6.4，Kip=0.013，Kii= 2.72。

当控制器采用常规PI控制，PI参数分别取上述理论计算值和实验整定后得到的理想参数时，得到的直流电压输出如图7所示。图7中波形(a)为PI参数取为理论计算值时的电压输出，此时输出结果不理想，存在较大的超调量，调整时间也较长。而通过实验整定，直流电压输出可以变得更理想，如图7中波形(b)所示。

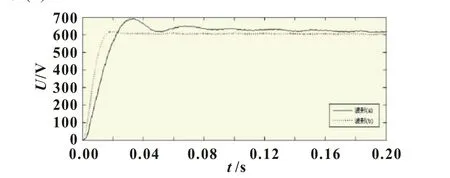
图7　参数整定前后的电压输出

3.3模糊PI控制与常规PI控制的比较

当控制器分别采用常规PI模块和模糊PI控制器时，直流电压输出如图8中(a)、(b)所示。通过比较得，采用模糊PI控制时，系统超调量变小，调整时间变小，具有更好的响应性能。

图8　PI控制方式不同时电压输出

当系统遇到负载突变等外部扰动时，采用常规PI模块和采用模糊PI控制器的电压输出分别如图9中(a)、(b)所示。由图9可得，采用模糊PI控制器的系统具有更高的稳定性和鲁棒性。

图9　负载突变时电压输出

4 结论

本文提出了一种基于模糊PI控制的整流器设计方案，可以实现在线实时地调整PI参数，从而使得系统获得更好的响应性能，且此方案设计简单，易于数字化实现。利用Matlab仿真对该设计方案进行了实验验证，结果表明本文的设计方法是正确的、有效的。

[1]PEREZ M,ORTEGA R.Passivity-based PI control of switched power converters[J].IEEE Transactions on Control Systems Technology,2004,12(6):881-890.

[2]张兴，张崇巍.PWM整流器及其控制[M].北京：机械工业出版社，2013.

[3]汪万伟，尹华杰，管霖.双闭环矢量控制的电压型PWM整流器参数整定[J].电工技术学报，2010(2)：67-72.

[4]庞科旺，刘丽丽，袁文华.基于模糊PID参数自整定的三相电压型PWM整流器控制[J].江苏科技大学学报：自然科学版，2008 (3)：57-61.

[5]任先文，王坤，余志飞.基于DSP的三相电压型整流器[J].电力自动化设备，2010，3：116-120.

[6]熊健，张凯，陈坚.PWM整流器的控制器工程化设计方法[J].电工电能新技术，2002，3：44-48.

[7]张崇巍，李汉强.运动控制系统[M].武汉：武汉理工大学出版社，2002.

[8]朱永亮，马惠，张宗濂.三相高功率因数PWM整流器双闭环控制系统设计[J].电力自动化设备，2006(11)：87-90.

[9]瞿博，吕征宇.三相电压型PWM整流器小信号建模及其控制器设计[J].电工技术学报，2010(5)：103-108.

[10]郑良广，孙泽文.基于模糊PI控制的三相高功率因数整流器[J].控制工程，2009(S3)：105-107.

[11]刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2003.

[12]林飞，杜欣.电力电子应用技术的MATLAB仿真[M].北京：中国电力出版社，2009.

[13]薛定宇.基于MATLAB/Simulink系统仿真技术与应用[M].北京：清华大学出版社，2005.

[14]尹泉，刘行，王庆义.三相电压型PWM整流器主电路参数设计[J].变频器世界，2011(12)：56-59.

Design of PWM rectifier based on fuzzy PI controller

SHAO Ze-long,SHI Ming-quan,HAN Zhen-feng
(Chongqing Institute of Green and Intelligent Technology,Chinese Academy of Science,Chongqing 400714,China)

An effective control method for three-phase voltage source PWM rectifier based on fuzzy controller was proposed to solve the problem,which PI parameters obtained by some simple mathematical model of the PWM Rectifier were uncoordinated to achieve a good system response performance.Compared with conventional PI control method,PI parameters could be automatically changed and the system was made better in response performance and in stability and robustness ability.Finally,a simulation model of the rectifier was built by the Matlab/ Simulink toolbox to prove the reasonable of the above design method.

PWM rectifier;double closed-loop control;fuzzy PI control;parameter setting;simulation

TM 461

A

1002-087 X(2016)01-0177-03

2015-06-12

邵泽龙(1989—)，男，山东省人，硕士，主要研究方向为计算机控制系统。