基于网格搜索优化LS_SVM蓄电池SOC估测

李韦韦，　朱　飞，　丁维明(.东南大学能源与环境学院，江苏南京0096；.江苏中瀚通信技术有限公司，江苏扬州500)

基于网格搜索优化LS_SVM蓄电池SOC估测

李韦韦1，朱飞2，丁维明1
(1.东南大学能源与环境学院，江苏南京210096；2.江苏中瀚通信技术有限公司，江苏扬州225200)

依据最小二乘支持向量机(LS_SVM)的基本理论，针对蓄电池荷电状态(state of charge,SOC)随温度、电压、电流而变化的特点，建立基于LS-SVM支持向量机的蓄电池SOC估测模型。通过数据验证，比较不同核函数下的效果，利用网格搜索寻找最优参数。观察在最优参数和最优核函数下LS_SVM支持向量机的预测效果。结果表明，与其他算法相比，采用RBF核函数，并用网格搜索优化的LS_SVM模型精度较高，适合用在蓄电池的SOC估测上。

蓄电池；SOC；最小二乘支持向量机；核函数；网格搜索

荷电状态(state of charge,SOC)是蓄电池额定容量和放电量的差与额定容量的比值[1]。当电量达到全满时，荷电状态为1，当净放电为额定容量时，荷电状态是0。在通信领域，蓄电池主要用于通信基站和中心机房作为后备电源。当市电中断，为避免中心设备中断造成重大损失，蓄电池必须有足够的供电量，保证正常供电，直到市电恢复。因此有效估测蓄电池SOC具有重要意义，可以避免蓄电池组电量不足而造成设备断电，降低维护费用。

经典的SOC估测方法是建立可测变量与SOC的辨识模型。常用的可测变量分为内部参数变量(电解液或活性物质参数)和外部参数变量(温度、电压、电流)[2]，内部参数需要使用特殊传感器，这将导致估测成本提高，外部参数的获取则相对简单。常用的辨识模型是基于等效电路或经验方程的数学模型，模型参数主要通过实验数据获得，精度较差。

由于外部参数与蓄电池SOC呈非线性特性，本文将引入最小二乘支持向量机(LS_SVM)，利用其对采集的数据进行建模及训练。LS_SVM是由Suykens在SVM基础上提出的一种方法，它采用最小二乘线性系统作为损失函数，具有较强的学习泛化能力，可以实现非常好的非线性建模[3]。

1 最小二乘支持向量机原理

当训练集{(x1,y1),(x2,y2),…(xn,yn)}为非线性时，LS_SVM通过某一非线性函数φ(·)将非线性数据映射到一个高维线性特征空间，在这个高维线性空间中构造回归估计函数。这种非线性变换通过核函数K(xi,yi)来实现。其中K(xi,xj)=φ(xi)φ(xj)，φ(xi)为一非线性函数。常用的核函数有以下几种[4]：

式中：w为与特征空间维数相等的向量。

为了使式(1)的估计实际风险最小，构造以下最小化目标函数，即对应的最优化问题：

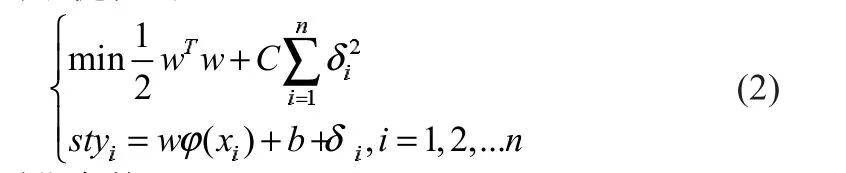
式中：C为正则化参数。

通过Lagrange将式(2)转化为二次规划问题：

再通过KKT最优化条件将式(3)转变为：

可得：

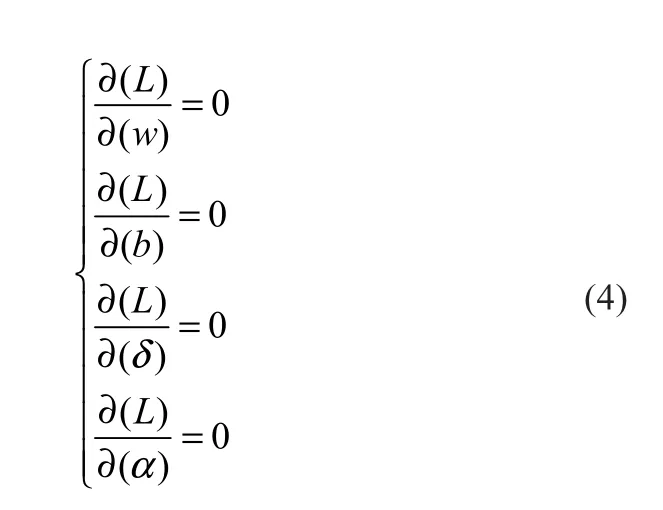
通过定义的核函数，可将式(5)转换为线性方程组的求解。最终得到以下回归估计函数：

2 基于LS_SVM的蓄电池SOC预测模型及实验

2.1数据的处理及模型的建立

本文利用江苏中瀚通信技术有限公司在扬州电信建立的《蓄电池远程维护与评估系统》中的蓄电池核对性放电实验数据，对扬州邗气通信站某500 Ah VRLA蓄电池放电过程进行建模。蓄电池从满荷状态开始放电，每2.5 s记录下蓄电池的端电压、电流、环境温度、放电时间、放电量等数据。根据SOC定义计算出蓄电池每个时刻的SOC，得到模拟所需的数据集。从中选取500组数据进行模拟，随机抽取250组样本数据作为训练样本，剩余250组作为测试样本。

研究表明SOC的大小与蓄电池的放电电流I和端电压U直接相关。此外，蓄电池的容量还会受到温度的影响，当环境温度升高，蓄电池的容量将增加，反之减少[5]。因此本文还选择蓄电池的表面温度T作为输入变量。可得到LS_SVM支持向量机辨识系统的输入变量为放电电流、端电压和蓄电池表面温度，即x=(U,I,T)T。输出为y=SOC。预测模型如图1所示。

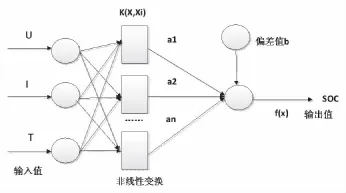
图1　LS_SVM预测SOC非线性模型

由于输入数据x=(U,I,T)T为多变量，且U、I、T三个变量的变化范围相差较大，为了加快模型的收敛速度，用极差化即式(7)对数据进行标准化处理，将原始数映射到0～1范围内。

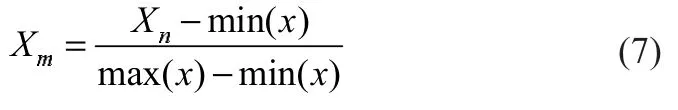
式中：Xn为原始数据；Xm为标准化数据；max(x)、min(x)分别为各变量最大值和最小值。

2.2核函数选取

使用预处理过的数据训练基于LS_SVM的SOC预测模型。首先，核函数的选择很大程度上影响了LS_SVM的性能。但是针对具体问题，至今也没有很好的方法指导核函数的选择。另外参数选取的好坏也将直接影响模型的辨识能力。因此核函数K(x,xi)的选择及参数的选取是本次研究的核心内容。

本文将分别比较RBF、poly、sigmoid三种核函数下的LS_SVM模型，通过比较模型精度选择合适的核函数。以均方差为精度检测的评价参数为：

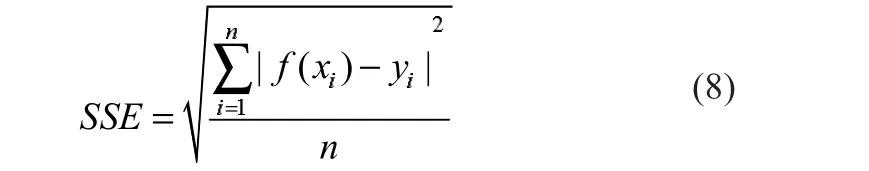
在确定核函数后，用式凑法选择合适的参数。首先给正则化参数C和核函数固有的参数赋一初始值，根据测试精度重复调整参数值，直至满意为止。得到的三种核函数参数如下。RBF：C=50，γ=－0.1；sigmoid：C=10，γ=－0.2，r2=0.4；poly：C= 10，γ=－0.1，r=1，d=2。图2所示为三种核函数下LS_SVM预测效果及误差对比。表1为对应的均方差和运行时间。

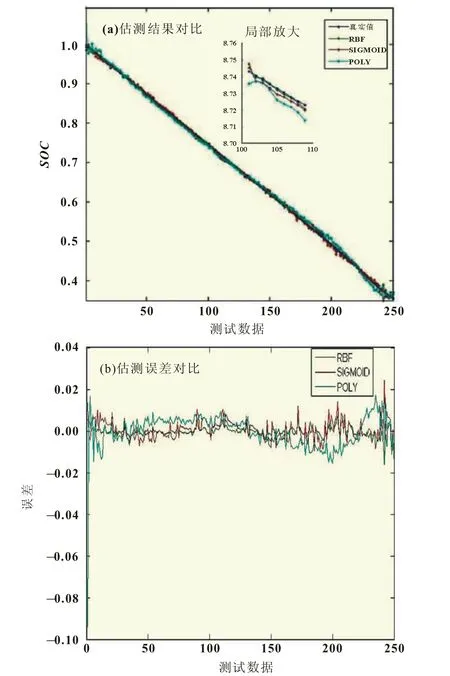
图2　　三种核函数下SOC预测效果及误差对比

??????????? ??? 　RBF 　sigmoid 　poly SSE/％ 　0.27 　0.47 　0.88 t/s 　0.177 238 　0.203 553 　0.119 728

实验结果表明，基于RBF核函数的LV_SVM的蓄电池SOC拟合效果最好，sigmoid核函数其次，而poly核函数拟合效果最差。poly函数属于全局性的核函数，泛化能力较好，但是当d值增大时，决策函数的复杂程度也会增大，使结构风险变大，降低算法的泛化能力。RBF函数是一种局部性的核函数，对局部影响较大，有时泛化能力较差。但是，其有很好的学习能力和适用能力，通过选取合适的参数γ，可减少其泛化能力差的缺点。sigmoid核函数效果则是介于这两种之间。因此RBF更适合用于蓄电池SOC估测。

实验中发现参数是影响LS_SVM效果的关键因素。正则化参数选取得越大，意味着所有训练样本都要准确逼近，对应的均方误差则减小，但这将导致算法复杂度提高，运行时间变长，降低了学习效率，因此C的选取要结合实际应用。而核函数的参数也对训练误差有很大影响。因此需对两者进行优化。

2.3参数优化及结果分析

为了达到更好的SOC估测效果，本文使用网格搜索的方法优化参数[6]。先设定网格搜索C、γ值的范围和搜索步长。这里设置C=104～0，步长为－1；γ=0～100，步长为0.01。这样C和γ的组合就有104×104，依次用每一种组合训练LS_SVM模型，然后选择预测精度最高的一组参数作为最优C、γ。本次网格搜索后的最优参数为：C=5 872，γ=7.64，均方差SSE= 0.001 7。优化后的SOC估测结果及另外两种算法的估测结果如图3所示。

从网格优化LS_SVM算法与其他算法的比较结果可以看出，采用BP神经网络虽然时间较短，但是误差太大，不能满足SOC估测的实际需求。而LS_SVM算法总体误差较小，也能满足SOC估测的精度要求，但网格优化后的LS_SVM误差更小，且网格搜索每个(C，γ)对都是相互独立的，可并行性高，学习速度快，预测出的蓄电池SOC和实际SOC曲线几乎完全一致，所以利用网格搜索进行参数优化后的LS_SVM对蓄电池SOC预测精度更高，完全能满足实际的需求。

最后为检测和评估网格优化后的LS_SVM算法对独立训练数据的数据集的泛化能力，避免过拟合，采用K折交叉验证(K-folder cross-validation，K-CV)[7]，将原来的500组蓄电池数据分成10个子集，每个子集均做一次测试集，其余9个集合作为训练集，K-CV交叉验证重复10次，并将10次的评价交叉验证误差作为结果。实验结果如表2所示。

参数优化后的算法泛化能力很好，且SOC均方误差为0.136％，完全满足SOC估测精度要求。

3结论

本文利用LS_SVM建立了蓄电池SOC估测模型，分析了与SOC相关的影响因素，提出了(端电压，电流，温度)-SOC模型，通过数据对模型进行训练。通过理论分析、仿真实验表明，利用RBF核函数建立的LS_SVM模型能够有效地估测蓄电池SOC。而根据网格搜索进行参数寻优后得到的模型参数应用在LS_SVM中可以使SOC估测具有更高的精度，并且优于BP神经网络，具有很好的泛化能力，适合应用于通信基站蓄电池SOC在线监测。

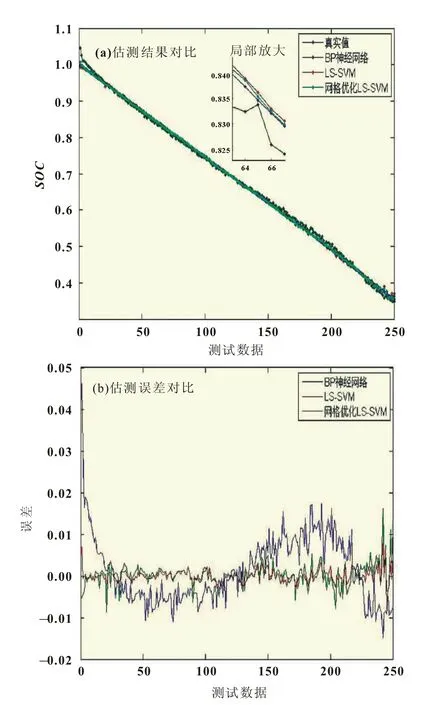
图3　　不同算法的SOC估测效果及误差对比

???????????? SSE SSE SSE SSE SSE ??? 0. 0 0 1 7 0 0 .0 0 1 3 0 0 .0 0 1 4 0 0 . 0 01 20 0 .0 0 1 2 0 0 .0 0 1 3 0 0. 0 0 1 2 0 0. 0 01 2 0 0 . 0 01 30 0 . 00 1 8 0 0 .0 0 1 3 6

[1]RAND D A J.阀控式铅酸蓄电池[M].北京：机械工业出版社，2007：184.

[2]陶兴华，陈彪，张俊.模糊逻辑与神经网络的蓄电池容量预测[J].电源技术，2004(9)：578-581.

[3]杜树新，吴铁军.用于回归估计的支持向量机方法[J].系统仿真学报，2003(11)：1580-1585.

[4]荣海娜，张葛祥，金炜东.系统辨识中支持向量机核函数及其参数的研究[J].系统仿真学报，2006(11)：3204-3208.

[5]梁敬.浅议影响阀控式铅酸蓄电池使用寿命的因素[J].广东电力，2005(2)：19-21.

[6]王兴玲，李占斌.基于网格搜索的支持向量机核函数参数的确定[J].中国海洋大学学报，2005(9)：859-862.

[7]王凯，侯著荣，王聪丽.基于交叉验证SVM的网格入侵检测[J].测试技术学报，2010(5)：419-423.

Battery SOC estimation based on LS_SVM optimized by grid search

LI Wei-wei1,ZHU Fei2,DING Wei-ming1
(1.School of Energy and Environment,Southeast University,Nanjing Jiangsu 210096,China;2.JiangSu Zhonghan Comunication Technology CO.,LTD.,Yangzhou Jiangsu 225200,China)

The basic theories of the LS_SVM(Least Square Support Vector Machine)were introduced.According to the battery SOC affected by temperature,voltage and current,the battery SOC estimate model based on LS_SVM was built.After training the LS_SVM model by experiment data,three kinds of kernel were compared in the mode and the best parameters were searched by using the grid search.The results show that RBF kernel and the grid search are the best for LS_SVM,and LS_SVM is very suitable for the prediction of SOC.

battery;SOC;LS_SVM;kernel;grid search

TM 912

A

1002-087 X(2016)01-0105-03

2015-06-12

李韦韦(1990—)，女，江苏省人，硕士研究生，主要研究方向为能源信息及自动化。