基于MIV的BP神经网络磷酸铁锂电池寿命预测

张金国，　王小君，　朱　洁，　迟忠君(.北京交通大学电气工程学院，北京00044；.北京电力公司北京电力科学研究院，北京00075)

基于MIV的BP神经网络磷酸铁锂电池寿命预测

张金国1，王小君1，朱洁2，迟忠君2
(1.北京交通大学电气工程学院，北京100044；2.北京电力公司北京电力科学研究院，北京100075)

针对锂离子电池循环寿命衰减问题，为了能更加准确地对锂离子电池的循环寿命进行预测，对磷酸铁锂电池全生命周期进行循环充放电测试，获得其相关性能参数，提出基于BP神经网络分析方法建立寿命预测模型。在预测模型基础上，运用平均影响值(MIV)算法筛选模型的输入参数。结果表明，所建立的电池循环寿命预测模型具有较高的精度，符合电池的实际运行特性，对解决电池寿命评估周期长和成本高等问题具有重要意义。

磷酸铁锂；循环寿命；神经网络；MIV

动力电池在实际运行中将受到很多外界因素的影响，往往达不到我们所预期的寿命值。过早更换会造成经济损失，不及时更换又会对系统稳定性造成极大的影响。因此，如果准确了解电池的寿命状态，无疑能找到经济性和可靠性的平衡点[1-3]。

目前，判断电池循环寿命的常用方法是通过对电池进行充放电循环实验，这种方法有一个比较大的缺点是测试时间比较长，有时甚至需要数月的时间，耗费巨大的人力物力，效率低下。如何在较短的时间内预测电池的寿命非常重要[4]。国外对电池循环寿命预测的方法主要分为两类：基于经验的方法和基于性能的方法[5]。文献[6]通过对恒流循环、工况循环及储存实验等方法，分析探讨磷酸铁锂动力电池在循环过程中的失效机理，但是并未在此基础上建立循环寿命的评价方法。文献[7]提出了一种通过拟合、回归的分析方法来建立可预测锂离子电池循环寿命的经验模型，但是由于实验数据缺少，仍存在一定的误差。

本文通过对磷酸铁锂电池进行1 200次的循环寿命测试获得性能参数，充分考虑了影响循环寿命的各个关键因素，以充电截止总电压、放电截止总电压、单体一致性(单体最大压差)、电池内阻为输入，基于BP神经网络方法建立电池循环寿命预测模型。运用平均影响值(MIV)算法[8-10]对输入参数进行筛选，提高预测精度。

1 基于BP神经网络的电池循环寿命预测模型

BP神经网络是一种多层前馈神经网络，该网络的主要特点是信号前向传递，误差反向传播。在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层。每一层的神经元状态只影响下一层神经元状态。如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络权值和阈值，从而使BP神经网络预测输出不断逼近期望输出[11-12]。BP神经网络拓扑如图1所示。

1.1网络结构搭建

网络输入层选择影响电池循环寿命的各个因素作为输入参数，具体为：充电截止总电压a1，放电截止总电压a2，单体一致性a3，电池内阻a4。输出参数为电池循环放电容量y。网络隐含层输出H根据输入向量X，输入层和隐含层连接权值ωij以及隐含层阈值a计算得出，计算公式为：

图1　BP神经网络拓扑结构

式中：f为隐含层激励函数，计算公式为：

l为隐含层的节点数，根据式(3)计算，即：

n为输入层节点数。网络的输出层输出则由隐含层输出H、连接权值和阈值b计算得出，计算公式为：

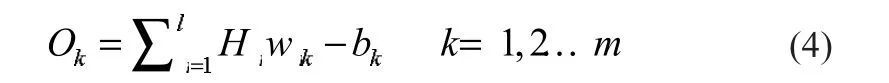
同时为消除原变量因量纲不同，数值差异太大带来的影响，需对原变量作归一化处理，即：

式中：xmin为数据序列中最小值；xmax为数据序列中最大值。

1.2训练样本获取

本文研究对象为国内某厂家提供的同一批次磷酸铁锂的锂离子电池，单体容量60 Ah，充电截止电压为3.65 V，放电截止电压2.0 V，标称电压为3.2 V，成组电池为24串，成组规格80 V/60 A。

为获得动力电池整个在运周期的运行特性，以保证测试样本的完整性和预测精度，采用如下实验方法：使用EVT 150 V/100 A动力电池测试设备对电池组进行1 200次循环的寿命测试。在(20±5)℃工作温度下，以0.5C恒流进行充电，至成组总电压3.6 nV(n=24)时转恒压充电，充电电流降至0.03C或单体电压达到3.65 V时停止充电，静置15 min，然后以1C进行放电，至成组总电压为2.7 nV或单体电压为2.0 V时停止，再静置15 min，动力电池一个循环测试周期完成，然后进入下一个循环周期。测试设备实时记录动力电池充放电曲线、充放电容量、充放电截止电压、电池内阻等。

电池在生命周期初始阶段各参数特性相对稳定，没有实际的预测意义，而在循环1 000次后，容量往往快速衰减，性能很不稳定[13]。因此，本文选取400～1 100次的测试数据(表1为网络输入参数的部分数据)作为训练对象，对1 100～1 200次的放电容量进行网络预测。

???????????????????? ???? ????/Ah ???????/V ???????/V ?????/mV ???? 4 0 1 　6 0 .8 0 　8 5 .5 3 　6 4 .8 0 　3 1 9 .9 　24 . 3 6 0 4 0 2 　6 0 .8 2 　8 5 .6 4 　6 4 .8 0 　2 9 8 .8 　24 . 4 0 1 4 0 3 　6 0 .7 9 　8 5 .5 4 　6 4 .7 9 　3 0 5 .0 　24 . 4 4 2 4 0 4 　6 0 .8 5 　8 5 .6 1 　6 4 .7 4 　3 1 6 .6 　24 . 4 8 3 4 0 5 　6 0 .8 3 　8 5 .6 3 　6 4 .7 7 　3 1 6 .2 　24 . 5 2 4 4 0 6 　6 0 .7 4 　8 5 .5 7 　6 4 .7 7 　3 2 4 .6 　24 . 5 6 5 4 0 7 　6 0 .8 0 　8 5 .7 1 　6 4 .7 8 　3 1 8 .1 　24 . 6 0 6 4 0 8 　6 0 .6 9 　8 5 .6 2 　6 4 .7 9 　3 0 8 .2 　24 . 6 4 7 4 0 9 　6 0 .7 1 　8 5 .8 4 　6 4 .7 9 　3 0 6 .0 　24 . 6 8 8 4 1 0 　6 0 .6 4 　8 5 .5 9 　6 4 .7 5 　3 1 4 .4 　24 . 7 2 9 4 1 1 　6 0 .7 3 　8 5 .8 1 　6 4 .7 3 　3 1 5 .6 　24 . 7 7 0 4 1 2 　6 0 .7 3 　8 5 .7 8 　6 4 .7 7 　3 2 0 .5 　24 . 8 1 1 4 1 3 　6 0 .6 5 　8 5 . 80 　6 4 .7 7 　3 1 6 .2 　24 . 8 5 2 4 1 4 　6 0 .6 6 　8 5 .7 7 　6 4 .7 4 　2 9 9 .1 　24 . 8 9 3 4 1 5 　6 0 .6 8 　8 5 .8 4 　6 4 .7 8 　3 1 4 .7 　24 . 9 3 4

1.3BP神经网络模型仿真结果

通过反复调试BP神经网络参数，最终确定迭代次数epo=100，学习率lr=0.1，训练目标goal=0.000 04，得到如图2所示的实测数据和预测数据对比，以及如图3所示的网络预测误差。

由图2、图3可知，采用BP神经网络基本能够达到预测电池循环放电容量的目的。但是，训练之后的相对误差较大，最大相对误差达到11％左右，预测相对误差大于5％的样本数占测试样本总数的30％左右，说明误差较大并非突变，而是预测精度达不到要求。尤其在电池生命周期末端，相对误差呈现递增趋势，而末端数据的准确性对本次预测有重要意义。

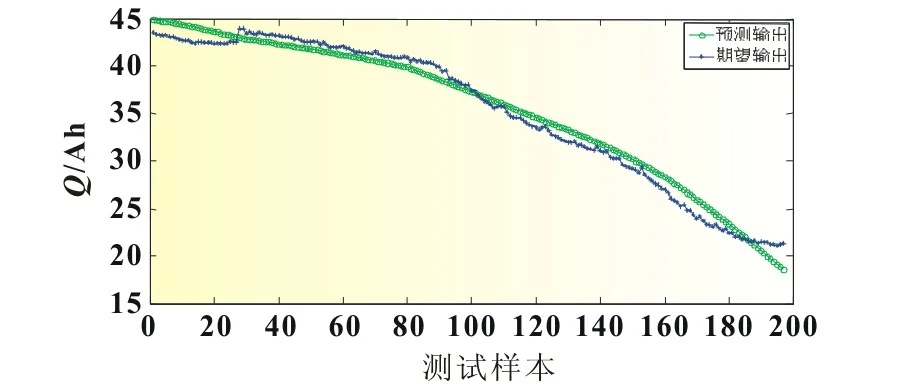
图2　BP网络预测输出

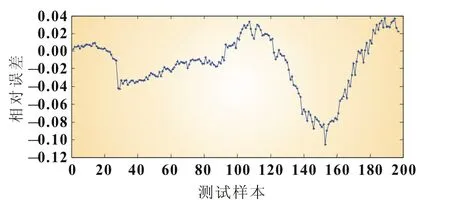
图3　BP网络预测输出误差

2 MIV算法筛选网络变量

经分析，训练样本数量的多少及质量的好坏对BP神经网络预测的精度有较大的影响。一般情况下，神经网络所包含的的输入数据是研究人员根据专业知识或者经验预先选择好的，但是在实际应用中，由于神经网络所包含的自变量即输入特征难以预先确定，很容易将一些不重要的自变量也引入神经网络，会降低模型的精度[14]。因此，选择有意义的自变量数据作为网络的输入数据，是应用神经网络分析预测问题中很关键的一步。

2.1MIV评价计算

MIV算法目前被认为是在神经网络中评价变量相关性最好的指标之一[15]。其符号代表相关的方向，绝对值大小代表影响的重要性。因此，可用MIV算法来测定神经网络输入单元对输出单元的影响权重，具体实现过程为：

(1)在完成BP神经网络训练后，将训练样本中的每个变量分别加减10％，构成两个新的训练样本；

(2)将它们分别作为仿真样本，利用已建成的网络对其进行模拟仿真，可得到两个仿真结果；

(3)对这两个仿真结果进行差值计算，所得值即为该自变量变动对输出参数产生的影响变化值；

(4)由现有的样本数求取影响变化值得平均数，即可得到该自变量对应的MIV值；

(5)重复上述步骤，依次计算各自变量的MIV值；

(6)对计算出的各个变量的MIV值进行排序，得到各个输入参数对预测结果的影响权重。

依据上述方法，分别对网络输入参数的各个变量进行MIV值计算，结果如表2所示。

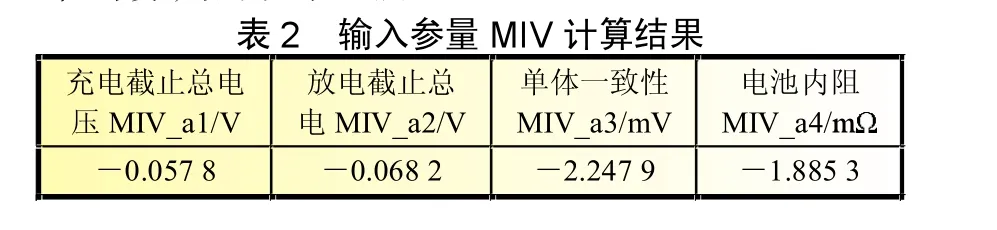
? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? MI V_ a1 /V ? ? ? ? ? ?M IV _a2/V? ? ? ?? MIV_ a3/ mV ? ? ? ? MI V_ a4 /? ? 0 . 0 5 7 8 　? 0 . 0 6 8 2 　? 2 .2 4 7 9 　? 1 . 8 8 5 3

由表2可知各个输入参数对输出结果的影响权重不一致。单体一致性对放电容量的影响最大，其权重值超过2.2，且单体一致性与放电容量呈负相关；电池内阻对放电容量的影响也较大，其权重值接近2，同样呈负相关；而充电截止总电压和放电截止总电压的权重值相对于单体一致性和电池内阻的权重值而言显得非常小，几乎可以忽略不计。筛选结果证明单体一致性和电池内阻是影响电池循环寿命的关键性因素。因此，网络在输入参数设置时选择单体一致性和电池内阻，以此简化网络结构，同时提高网络的预测精度。

2.2变量筛选后的模型仿真结果

经过变量筛选之后，利用单体一致性和电池内阻来预测电池循环放电容量，得到的实测数据和预测数据对比以及网络预测误差见图4、图5。

由图4和图5可知，通过MIV算法对输入参数进行筛选以后，网络预测的最大相对误差控制在5％以内，相较于之前的11％(图3)有很大改进。对前后两次预测结果分别求取均方根误差和平均相对误差，由表3可知通过MIV方法筛选以后，网络的预测精度得到了很大的提高，验证了MIV算法的有效性。

图4　　变量筛选后BP网络预测输出

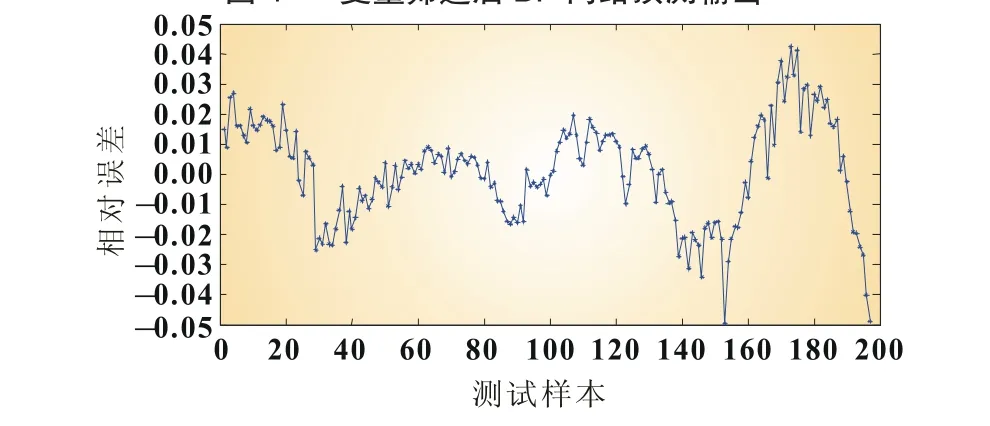
图5　　变量筛选后BP网络预测相对误差

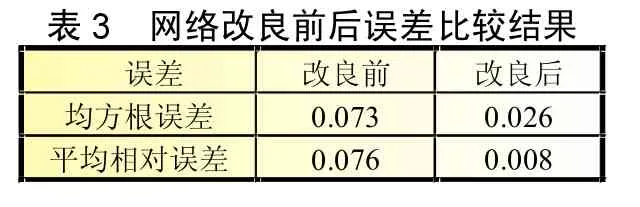
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ??? 　?? ? 　? ? ?? ? ? ? ? ? 　0 . 0 7 6 　0 . 0 0 8 ? ? ? ? ? 　0 . 0 7 3 　0 . 0 2 6

3 结论

本文针对磷酸铁锂电池循环寿命预测问题，建立了基于BP神经网络的电池放电容量预测模型，并采用MIV算法对输入参数进行了优选。通过实验得出以下结论：

(1)在影响电池循环寿命的众多因素中，单体一致性和电池内阻起主导作用，若将一些不重要的输入参数引入神经网络，会降低模型的精度；

(2)采用MIV算法优化后的BP神经网络预测模型在很大程度上提高了模型的精度，可用于电池放电容量的预测，有利于解决电池评估周期长和成本高等问题。

[1]YU H J,ZHANG T Z,YUAN J,et al.Trial study on EV battery recycling standardization development[J].Advanced Material Research,2012,610/613:2170-2173.

[2]王雪非.基于工况仿真的锂动力电池寿命研究[D].哈尔滨：哈尔滨理工大学，2011.

[3]高飞，杨凯，惠东，等.储能用磷酸铁锂电池循环寿命的能量分析[J].中国电机工程学报,2013,33(5):41-45.

[4]林成涛,李腾,田光宇,等.电动汽车用锂离子动力电池的寿命试验[J].电池,2010,40(1):23-26.

[5]罗伟林,张立强,吕超,等.锂离子电池寿命预测国外研究现状综述[J].电源学报,2013(1):140-144.

[6]赵淑红，吴锋，王子冬．磷酸铁锂动力电池工况循环性能研究[J]．电子元件与材料，2009，28(11)：43-47．

[7]孟祥峰,孙逢春,林程,等.动力电池循环寿命预测方法研究[J].电源技术,2009,33(11):955-958,969.

[8]王紫微,叶奇旺.基于神经网络MIV值分析的肿瘤基因信息提取[J].数学的实践与认识，2011,41(14)：47-58.

[9]王嘉寅.基于MIV特征筛选和BP神经网络的煤质特征分析[J].中国科技纵横,2012(13):38.

[10]孙文彬,刘希亮,王洪斌,等.基于MIV的抛掷爆破影响因子权重分析[J].中国矿业大学学报,2012,41(6):993-998.

[11]邓超,史鹏飞.基于神经网络的MH/Ni电池剩余容量预测[J].哈尔滨工业大学学报,2003,35(11):1405-1408.

[12]项宇,刘春光,苏建强,等.基于BP神经网络的动力电池SOC预测模型与优化[J].电源技术,2013,37(6):963-965,986.

[13]吴赟,蒋新华,解晶莹,等.锂离子电池循环寿命快速衰减的原因[J].电池,2009,39(4):206-207.

[14]史峰,王小川,郁磊,等．Matlab神经网络30个案例分析[M]．北京：北京航空航天大学出版社,2010：183.

[15]顾瑶媛,谢红,吴旭波,等.基于MIV特征筛选和BP神经网络的三维人体参数转换[J].上海工程技术大学学报,2012,26(4):361-364.

Cycle life prediction of LiFePO4Li-ion battery based on MIV Algorithm and BP Neural Network

ZHANG Jin-guo1,WANG Xiao-jun1,ZHU Jie2,CHI Zhong-jun2
(1.School of Electrical Engineering,Beijing Jiaotong University,Beijing 100044,China;2.Beijing Electric Power Research Institute, Beijing Electric Power Company,Beijing 100075,China)

In order to deal with the declining of cycle life of lithium batteries and to predict their cycle life more accurately,a circulation test of charging and discharging during the whole lifecycle of lithium iron phosphate batteries was conducted and related performance parameter was got.Then a life prediction model was proposed based on the analytical method of BP network analysis.Based on the prediction model,the algorithm of mean influencing value (MIV)was applied to filter the input parameters of the model.The results indicate that the prediction model of cycle life of lithium batteries established possesses a higher precision,which is in accord with the actual running characteristic of the batteries and is of significance to solve the problems of long period and high cost of assessment of battery life.

LiFePO4;cycle-life;back-propagation(BP)neural network;mean impact value(MIV)

TM 912

A

1002-087 X(2016)01-0050-03

2015-06-05

国家电网公司科技项目(GWKJ201203)

张金国(1989—)，男，江苏省人，硕士，主要研究方向为电动汽车电池建模与电动汽车充电实时仿真测试。