一种改进小波阈值函数在医学图像消噪中的应用

李 宏，张思源

（东北石油大学 电气信息工程学院，黑龙江 大庆　163318）

一种改进小波阈值函数在医学图像消噪中的应用

李 宏，张思源

（东北石油大学 电气信息工程学院，黑龙江 大庆163318）

提出了一种用于医学图像消噪的新型的小波阈值函数。改进的阈值函数是将两种常见的软、硬小波阈值函数相结合并加以改进，使其兼具了两者的滤波消噪特性。同时将改进的小波阈值函数应用在医学图像图像处理中，用于消除医学图像的噪声干扰，并利用仿真实验与软硬阈值函数作对比，从效果图和实验数据分析验证了其优势。

小波变换；阈值函数；医学图像；图像消噪

从伦琴射线的发现到如今的计算机断层扫描、核磁共振成像等医学设备的广泛应用，医学图像为医生的病灶区诊断提供了有利依据，提高了医疗诊断的准确性。医学图像由于图像采集设备本身和采集环境的复杂性，使得医学图像在采集和传输的过程中总是掺杂来自多方面的噪声的干扰［1］，诸如：高斯噪声、锐利噪声等［2］，噪声的干扰直接影响到信息的准确度，尤其是对组织病灶区的图像信息的需求分析产生强烈的干扰。因此，基于医学图像的消噪的研究逐渐成为热门。

当前针对图像消噪传统的处理方法有很多，就目前的研究发展来看，图像消噪的算法大体可分为两种：一种为线性消噪法，另一种为非线性消噪法［3］。线性消噪法中比较经典是维纳滤波法，但是无法处理非平稳的随机过程的噪声，同时也无法应用于向量［4］。因此，在实际应用中通常不采用维纳滤波 。如今，非线性滤波法逐渐替代线性滤波成为图像消噪方向的主流，小波阈值消噪法就是较受青睐的方法之一。小波消噪方法的类型很多，比如：小波模极大值消噪，小波阈值消噪，小波变换尺度的相关性消噪等［5］。其中，小波阈值消噪法凭借其计算简易、处理简便的优势获得比较广泛的使用。小波阈值消噪法是在1995年由Dohono提出的，其核心是追求最优化问题［6］。小波阈值消噪在时域和频域范围内都能较好的针对局部进行分析和处理，小波的变尺度的特性使得小波将图像信号“聚集”。在大范围内，小波可平滑噪声，降低其的小波系数［7］。这样根据不同阈值系数处理信号，就可以达到降噪保真的效果。然而，传统的基于小波的软硬阈值函数消噪法是不完美的。硬阈值函数的不连续性和软阈值的边缘化模糊无法满足医学图像对图像信息的对连续性和边缘化的兼容性需求。

本文提出了一种新型的小波阈值函数，这种函数兼具了两种常见的软、硬函数的特性，可以根据图像对画面的不同需求设置系数以呈现不同的画面质感，同时利用MATLAB仿真实验结果也验证了改进阈值函数在医学图像消噪中的优势。

1　小波阈值消噪

1.1小波阈值消噪基本原理

小波变换去相关性相对较强 。图像信号自身位于较大的小波系数上，其经过小波变换后仍集中在较大的小波系数上，而噪声的能量对应较小的系数，是存在于整个小波域中的，因此就小波系数幅值来看，信号的幅值要大于噪声的幅值。因此，通过设定门限阈值能够达到保留信号去除噪声的效果。

通常情况下，普通的一维观测信号既包含了原始信号又包含了加性噪声，具体模式为：

其中s（t）为原始信号，n（t）为加性噪声信号。对F（t）离散采样可获得n点的离散信号，有：

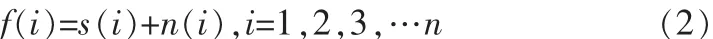
对式（2）小波变换为：

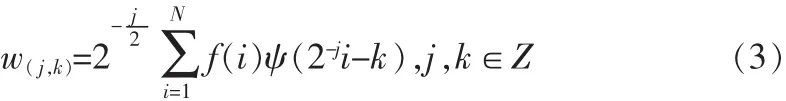
对于图像信号而言，待处理图像可由原始图像和高斯白噪声组成，具体的含噪图像模型为：

其中i，j=（1，2，…，n），n是像素的个数，s是初始图像信号，z是服从N（0，δ2）分布的高斯白噪声。可以看出，小波变化是一种线性变化，所以如果噪声为高斯白噪声，变换后仍具有高斯特性。根据上述特性，需要设置一个较适合的阈值，保留大于阈值的有用信号，滤掉小于阈值的噪声部分已到达消噪的目的。

小波阈值消噪的通常分为如下3个步骤：

1）对加有噪声图像的小波多级分离：先选取适应的小波函数，设置小波的分离层数，对含噪图像信号逐层分离，实现小波多级分解的过程。

2）小波滤波消噪处理：对经过逐层分离后的小波图像做阈值量化滤波处理，选取一个较好的阈值函数，确定阈值大小。提取高频系数部分，对其做阈值量化，即可获得新小波系数矩阵

在整个图像消噪过程中，小波阈值的消噪是整个过程的重要环节。阈值的选择一大部分程度上会影响消噪图像的画质。倘若保留大部分的高阈值部分，虽然可以过滤掉大部分噪声信号，但是对原有图像信息有损。相反，如果只保留大部分的低阈值部分，就会掺杂众多噪声信息。因此，对小波阈值函数的抉择是整个研究环节的重点内容。

1.2小波阈值消噪函数

常见的小波阈值消噪函数有两种：一种为硬阈值函数，另一种为软阈值函数。

1）硬阈值函数：这种方法能够获得大于阈值的小波系数，过滤掉小于阈值的部分可令其等于零，具体公式如下。

2）软阈值函数：软阈值是在硬阈值的进一步改造。

上述两个公式中为w（j，k）估计小波系数，为分解后的小波系数，λ为阈值。通过式（5）和式（6）不难发现，硬阈值虽能够复原像图像边缘这类的细节特征，但出现了类似于吉布斯效应的视觉失真。而软阈值的处理效果虽然相对较好，但是软阈值得到的复原图像相对平滑，使得重构图像与原始图像之间存在一定偏差。

1.3改进阈值消噪算法

针对上述两种函数存在的问题，若将两种类型的阈值函数加以结合，就可以得到一种新型的阈值消噪函数，其公式如下：

为了保证改进后的函数同时与两种函数保持一致性，对f（w（j，k），λ）有如下需求：

式（9）中，0＜m＜1。显然，式（10）同时满足式（8）和式（9）两个条件。这个方法的结构形式非常简单，就是将式（5）和式（6）有机的结合在一起，使改进后的函数同时获得两种函数的特性，相互弥补两种函数的不足。当m=1时，函数为硬阈值函数形式，当m=0时，函数为软阈值函数形式。但实际过程中，并不能m的范围两边取等号，否则就会失去函数改造的意义。因此m可选取（0，1）的中间值将。当m∈（0～0.5）时，阈值函数处于折衷阈值偏向于软阈值特性，适用于边缘较为丰富的图像，得到的消噪图像边缘相对会比较平滑。当m∈（0.5～1）时，阈值函数处于折衷阈值偏向于硬阈值特性，消噪后图像具有相对尖锐的边缘，使图像的边界较为清晰。进而可以针对各类图像需要选择m的大小。因此，改进的函数既兼具了阈值函数局部细节性好的特性，又具有软阈值函数平滑的双重特性。

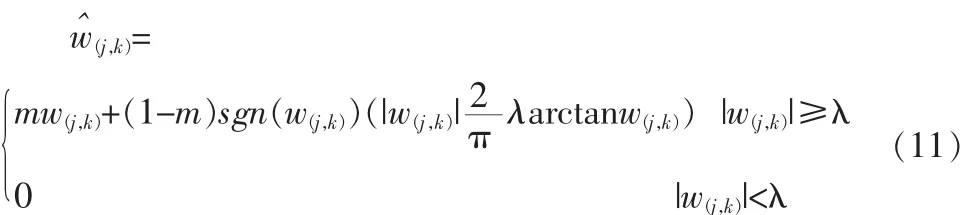
式（11）同式（10）一样，能够同时满足式（8）和式（9）的条件，同样具有软硬函数的兼具特性。

2　改进的算法在图像消噪中的应用

医学上，常用的二维图像通常是以 DICOM（DigitalImaging and Communication in Medical，医疗数位影像）格式输出的。DICOM是由具有一定标准要求的文件头和影像数据集相结合的二维断层序列医学图像。DICOM既存储了图像信息又包含了与患者相关的个人信息。本文选取DICOM图像作为原始图（如图1所示），采用了MATLAB R2008作为仿真系统平台。利用MATLAB中的dicomread（）语句能够读取DICOM的图信息。为体现改进后的阈值函数的消噪效果的优势，将其同软硬阈值函数的消噪效果进行实验比较。消噪过程如下（如图2所示）。

图1　原始图像

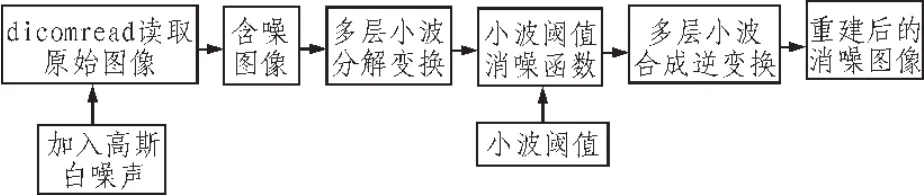
图2　小波阈值消噪流程图

1）在原始医学图像的基础上加入高斯白噪声（加噪图像如图3所示）模拟拍摄和读取的复杂环境，由于噪声对医学图像的影响非常大，相比普通图片，只需要加入系数很小的噪声就会对图像产生很大的干扰。文中采用的高斯白噪声的均值为0，方差为0.000 001。

图3　加噪图像

2）对加噪图像做二维信号的多层小波分解，文中选取sym4小波作为函数空间的基，对信号进行三层分解。

3）获取每层每一个高频分量中的坐标，提取其高频系数。

4）设定阈值λ，文中采用经典的VisuShrink阈值：

其中N为信号的长度，δ为噪声标准差，有：

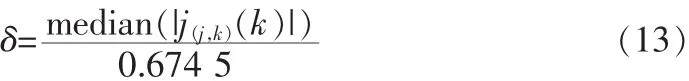
5）分别利用式（10）和式（11）对各高频系数进行阈值函数处理。由于选取的图像属于医学图像类，医学图像对于细节的要求高，同时边缘的要求尖锐，因此处理图像时选取m= 0.72，使得改进的阈值函数既侧重于硬阈值函数的特性又有软阈值函数的特性。由此，得到新的小波系数。

6）利用得到的系数做小波逆变换，将二维信号小波多层重组得到消噪后较为清晰的图像。

另外，采用峰值信噪比（PSNR）和最小均方误差（MSE）可作为消噪性能的评估指标。如果能获得较高的峰值信噪，较小的最小均方误差，则说明越接近真实的图像，小波阈值消噪的复原效果就越好。

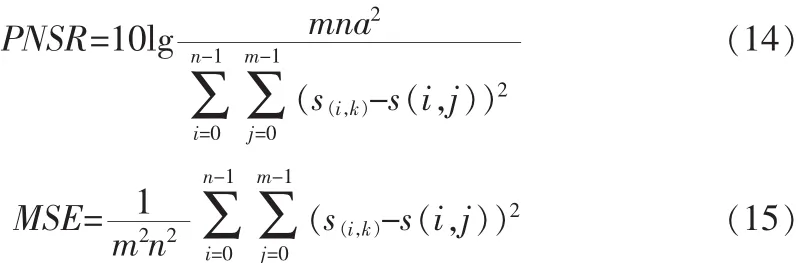
利用MATLAB对原始图像（如图1）加入高斯白噪声，加噪效果如图3所示。依据图2的流程图，利用小波变换将图像像素信息分成了3层，获取每层每个高频分量的坐标，提取每层高频系数并做阈值处理。本文分别利用软、硬阈值函数和两种改进的阈值函数进行图像消噪，相继得到了硬阈值函数消噪效果图（如图4）、软阈值函数消噪效果图（如图5）、利用式（10）作阈值函数时的消噪效果图（如图6）以及利用式（11）作阈值函数时的消噪效果图（如图7）。最后利用式（14）和式（15）对消噪的效果图进行评估，得到的评估数据如表1所示。

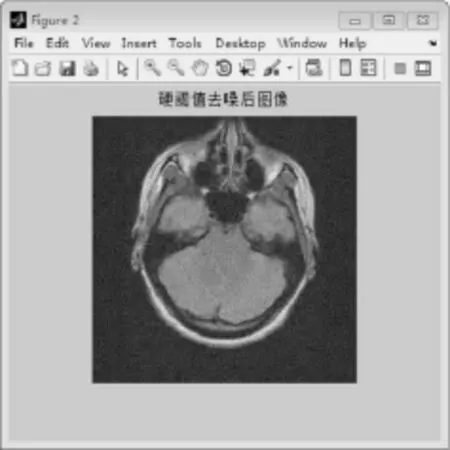
图4　硬阈值消噪图

上述结果经分析可知，利用硬阈值函数处理医学图像能够使图像画面存在明显的边缘化的效果，但是这种函数在阈值处的波动性大，会产生强烈的震荡，另外从数据分析来看硬阈值的信噪比最低，最小误差率较大。利用软阈值函数处理医学图像虽然从数据分析看信噪比和最小误差率占据优势，但是从式（5）与效果图5综合分析来看，在趋近阈值处逐渐趋近于零，由于真实值与阈值函数的小波系数存在横差，因此软阈值处理得到的重构信号使得图像平滑，与原有图相比存在很大的图像视觉失真。经过改进的两种函数不仅能够满足医学图像对边缘区域需要明显区分的要求，具有较大的PNSR和相对较小的MSE，表达出的图像相对于两种常见的函数处理图像相比较为清晰。从上述分析和图表信息等方面综合分析，经过改进后的两种小波阈值消噪函数在图像消噪方面具有较大的优势。

图5　软阈值消噪图

图6　改进I消噪图

图7　改进II消噪图

表1　5种图像的性能指标比较

3　结束语

文中介绍了小波阈值［8］消噪的基本原理和消噪流程，在常用的小波阈值消噪的基础上将软、硬阈值函数相结合并加以改进得到了两种新型的函数。同时，将阈值消噪函数应用到了医学图像消噪中并与两种函数作效果图和数值的相比分析。实验结果证明，改进的两种阈值函数具有相对较好的消噪性能，消噪后图像的峰值信噪比相对提升，误差明显减小，能够针对高斯白噪声相对较好的复原图像。

［1］王菲菲.小波在CT图像三维重建中的应用研究［D］.大庆：东北石油大学，2013.

［2］叶重元，黄永东.小波阈值消噪算法的新改进［J］.数字技术与应用，2011，47（12）：141-145.

［3］金宝龙，李辉.一种新的小波阈值去噪算法［J］.弹箭与制导学报，2011，32（1）：167-169.

［4］王小兵，汤海燕.小波变换在医学影像去噪和增强处理中的应用［J］.数字技术与应用，2011，6（1）：70-72.

［5］YANG Yong.Research on the choice of wavelet bases in wavelet image compression coding［J］.Science Technology Engineering，2011，11（10）：2747-2750.

［6］SHANG Li，ZHOU Yan，CHEN Jie，et al.Image denoising using a modified LNMF algorithm［J］.International Conference on Computer Science&Service System （CSSS），2012：1840-1843.

［7］李敏.小波阈值消噪中新函数的研究［J］.长春理工大学学报：自然科学版，2011，34（3）：176-178.

［8］宋倩倩，双凯.基于新阈值函数的小波阈值降噪方法［J］.电子设计工程，2014（1）：11-13.

An improved wavelet threshold function in the medical denoising image application

LI Hong，ZHANG Si-yuan
（Electrical&Information Engineering College，Northeast Petroleum University，Daqing 163318，China）

Paper presents a novel wavelet threshold function.Modified wavelet threshold function combines and improves two classical-hard and soft threshold functions wavelet threshold functions，which contains better denoising proprites of these two fuctions.Futhermore，the fuction can be applicated by medical denosiong image application.And simulation experiement can compare these fuctions with the novel one，and can prove its advantage by rendering and experiment data analysis.

wavelet transform；threshold function；medical image；denoising image

TN911.73

A

1674－6236（2016）09-0172-04

2015-05-26稿件编号：201505225

黑龙江省青年科学基金项目（QC20114C066）

李 宏（1969—），女，黑龙江依安人，博士，教授。研究方向：通信与信息系统，信号与信息处理，油气信息与控制工程。