两种拉伸实验的岩石细观参数反演分析

潘瑞凯，张开智，王树立，姬松涛

(1.山东科技大学矿业与安全工程学院，山东 青岛 266590；2.贵州理工学院矿业工程学院，贵州 贵阳 550003)



两种拉伸实验的岩石细观参数反演分析

潘瑞凯1，张开智2，王树立1，姬松涛1

(1.山东科技大学矿业与安全工程学院，山东 青岛 266590；2.贵州理工学院矿业工程学院，贵州 贵阳 550003)

将颗粒流程序应用于解决工程问题的前提是对岩石试件的几个力学参数进行准确标定，抗拉强度的标定便是其中之一。通过比较分析巴西实验和直接拉伸实验，结合具有非线性映射能力的BP神经网络，对颗粒流岩石的细观参数进行反演研究。表明：巴西实验条件苛刻，难以保证大量实验成功进行，无法向神经网络提供高质量训练样本，反演精度仅为61%；直接拉伸实验条件宽松，可以保证神经网络训练样本的数量和质量，反演精度可提高到83%；在保证样本数量和质量的前提下，BP神经网络有能力实现宏细观参数的准确映射，是颗粒流岩石参数标定的有效手段。

直接拉伸；人工神经网络；细观参数反演；巴西实验；颗粒流；离散元

1　文献综述

徐小敏等[1]基于线性接触模型建立了颗粒材料初始杨氏模量、初始泊松比等宏观弹性常数与颗粒法向刚度、颗粒刚度比等细观弹性常数间的经验公式。赵国彦等[2]对平行黏结模型中细观参数对宏观弹性模量和泊松比影响进行了研究。周博等[3]对黏性土类材料开展了不同围压下的平面双轴压缩试验，并依据摩尔-库仑强度准则对数值试样的剪切强度参数(内摩擦角、黏聚力)进行标定。尹成薇等[4]认为砂土内摩擦角与颗粒摩擦角之间满足线性关系，黏聚力与颗粒接触强度之间符合线性规律，且两者拟合曲线的斜率与颗粒摩擦系数之间呈现幂函数关系。上述学者主要通过进行大量的相关力学实验，进而用得出的宏细观参数数据进行函数拟合，从而得出某个独立的宏细观参数之间的经验公式，是宏观单参数对细观多参数映射，而非宏观多参数对细观多参数映射，因此，得出的经验公式具有一定的片面性。为此，周喻等[5]采用BP神经网络方法，建立了弹性模量、泊松比、抗压强度与细观力学参数的非线性模型；周梅等[6]利用神经网络预测混凝土的抗压强度。但结合岩石的抗拉强度进行颗粒流细观参数的研究尚未见相关报道。

本文基于人工智能理论中的BP神经网络模型，利用PFC3D进行巴西间接拉伸实验和直接拉伸实验，通过试验得出的大量数据对弹性模量、泊松比、抗拉强度和细观参数进行非线性映射，试图实现对给定岩石的颗粒流细观参数进行准确、快速地反演。值得一提的是，MATLAB自2010b版本后开发了完整的神经网络工具箱，提供了友好的GUI界面，用户只需要在命令行键入“nntool”即可打开神经网络工具箱。本文正是将PFC3D得出的大量实验数据进行整理后，输入神经网络工具箱进行后续的训练和仿真。

2　基于巴西间接拉伸实验的细观参数反演

本次试验通过单轴压缩实验测出岩石试样的弹性模量和泊松比，数值模型为矩形体，高为100mm，长、宽均为50mm；进行巴西实验测定岩石的抗拉强度，数值模型为直径50mm，厚12.5mm的圆盘，厚径比为1∶4，见图1。

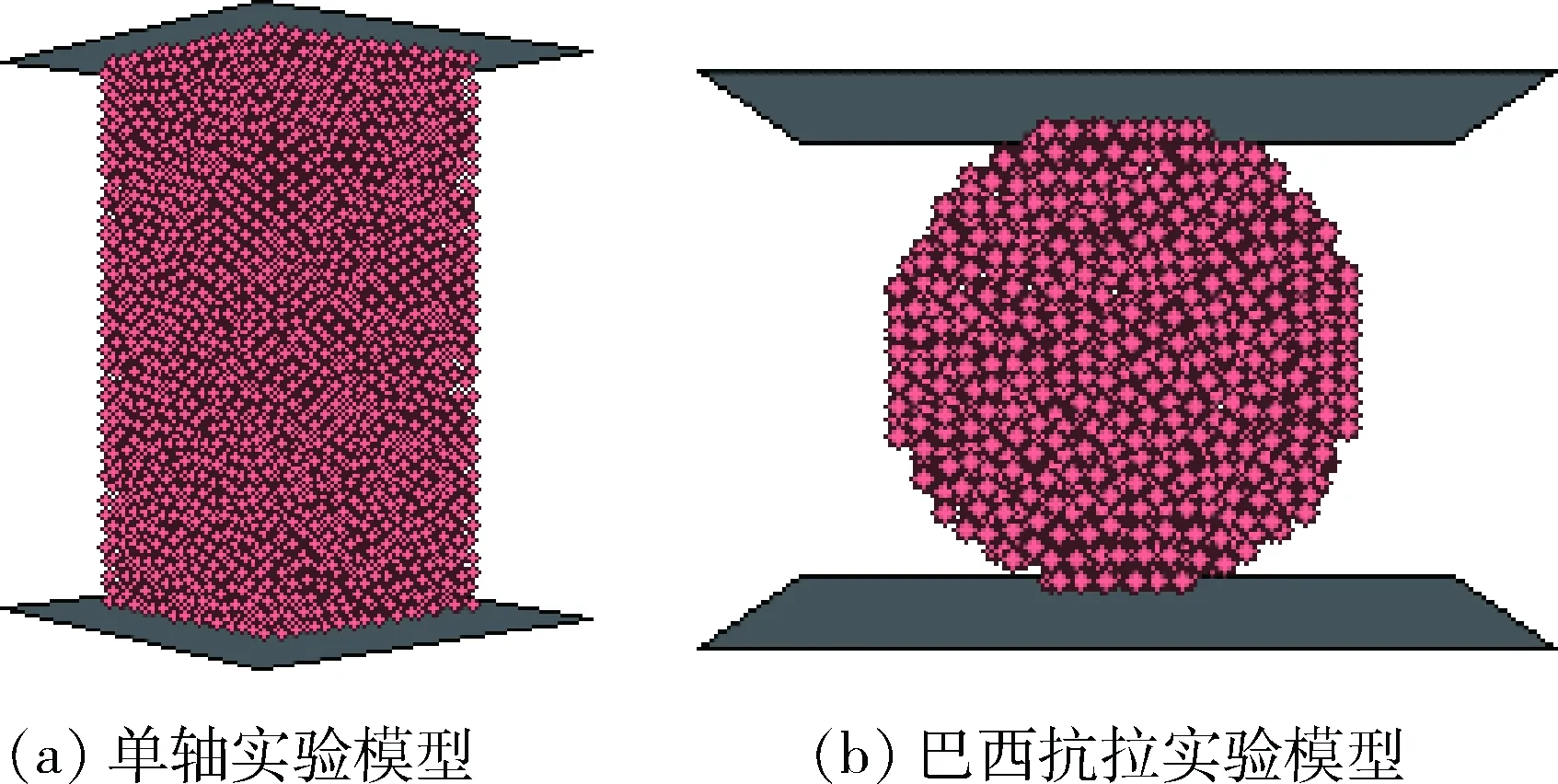
图1　颗粒流数值模型

2.1BP神经网络训练样本构造

进行标定的细观力学参数范围如下：Ec为10×109～70×109Pa；Kn/Ks为 1～4；μ为0.1～0.7；σc为15～90MPa；τc为15～90MPa，五个细观参数均划分为4个水平，如果要做全面试验，即将所考虑的各种水平做全面搭配，则要进行45=1024次试验，试验耗时长，实际情况不允许。为此考虑进行4水平5因素正交优化试验[8]，优化后需要做16次试验，各参数水平划分见表1。

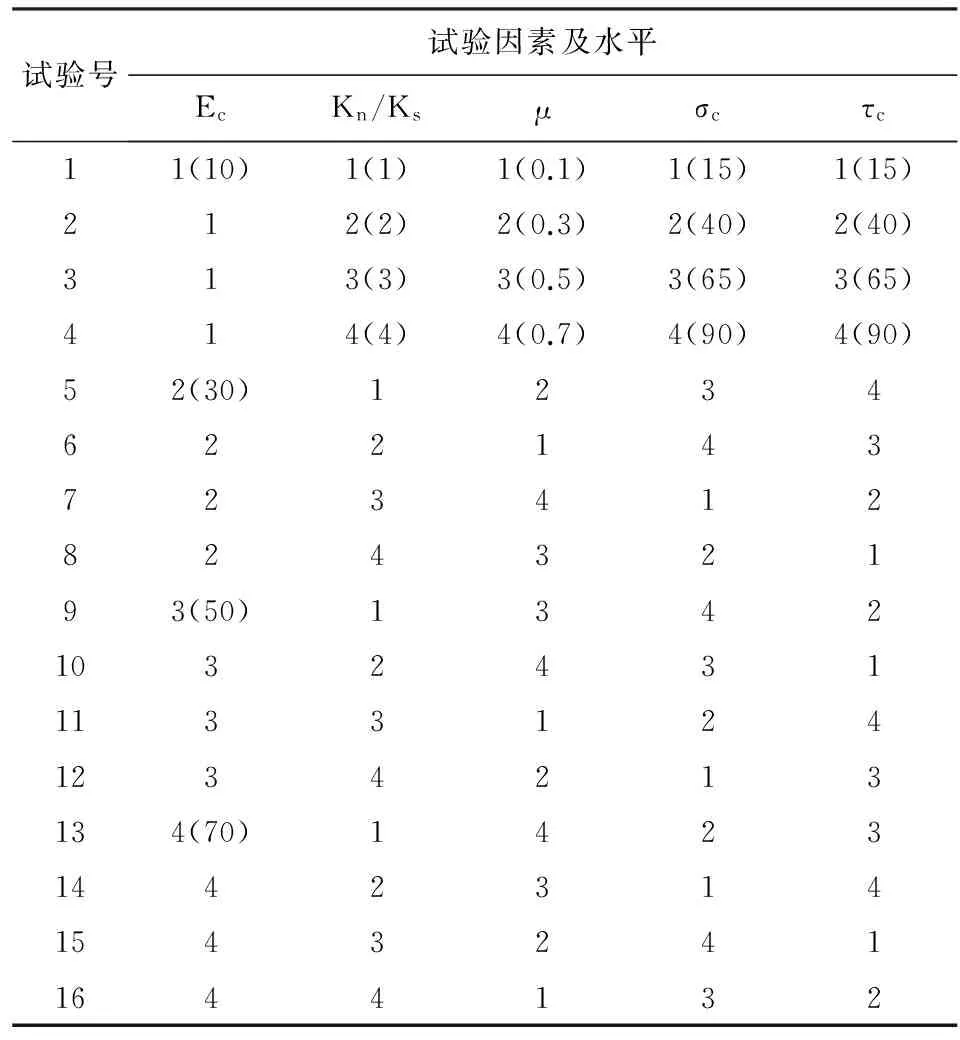
表1　正交实验设计(L1645)

根据表1选出的16组数据进行三轴实验和巴西实验。将实验得到的宏观力学参数作为输入样本向量，细观力学参数作为输出样本向量分别导入BP神经网络模型，然后进行网络训练与仿真。

2.2BP神经网络模型训练

网络训练函数采用trainlm函数，网络隐含层传递函数采用tansig函数，输出层传递函数采用purlin函数。网络性能函数采用均方误差函数mse。由于输入样本为3维输入向量，输出样本为5维输出向量，因此，输入层设置3个神经元，输出层设置5个神经元。隐含层神经元个数对网络性能影响较大，且难以确定。选取不同的隐含层神经元个数，建立多个BP神经网络模型，最终训练结果表明隐含层神经元为5个时训练效果好，图3为进行训练后的实际参数与神经网络输出参数的拟合效果。

2.3BP神经网络模型进行参数反演

随机选取4组PFC3D已经计算完成的宏细观参数，见表2。将宏观参数作为输入样本，调用训练完成的神经网络进行仿真，将网络输出的细观参数结果与进行PFC3D模拟的实际细观参数进行比较，得到反演结果的精度，精度值P[5]的定义见下式。

式中：b为BP网络输出细观参数值；B为实际细观参数值。

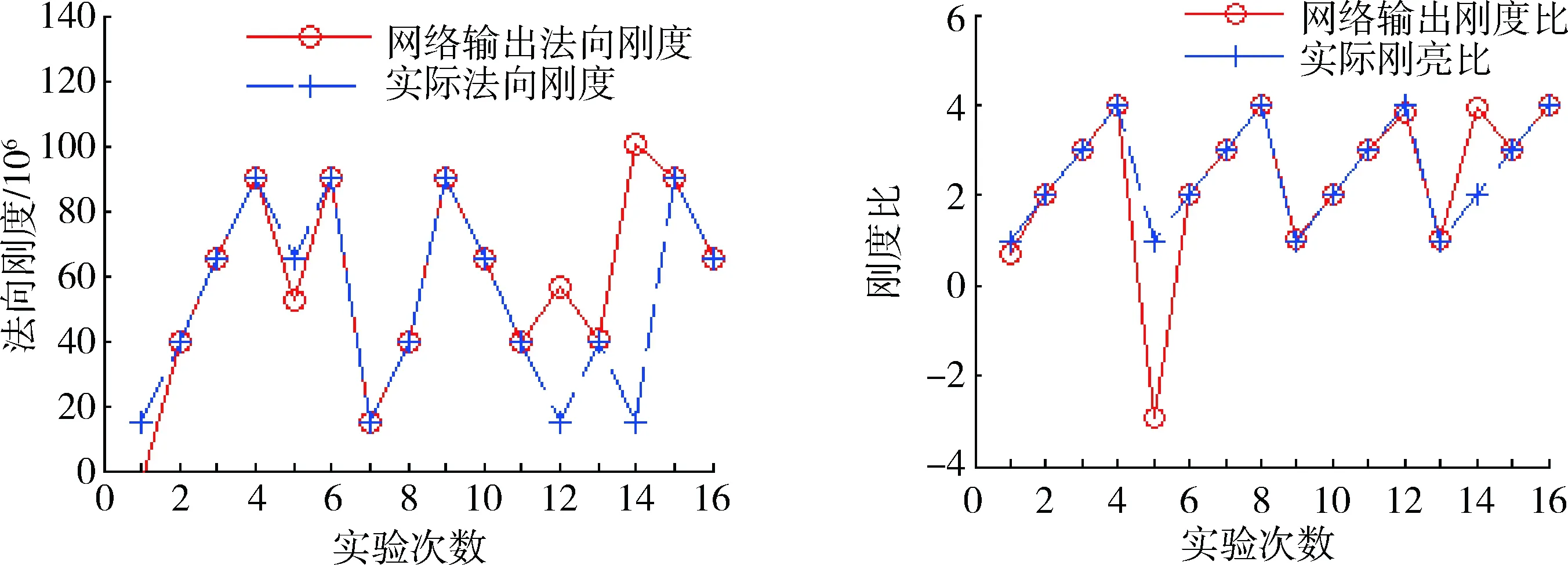
图2　巴西实验下的的训练效果

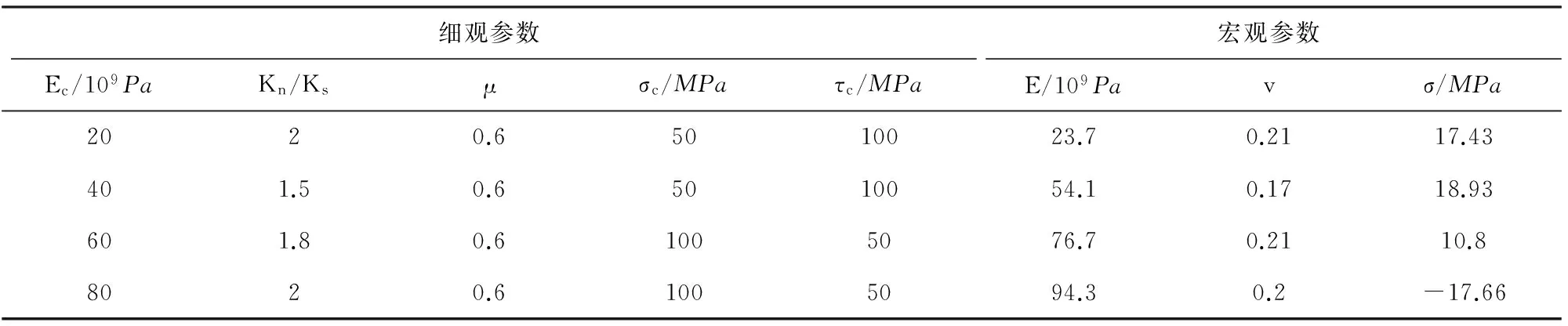
细观参数宏观参数Ec/109PaKn/Ksμσc/MPaτc/MPaE/109Pavσ/MPa2020.65010023.70.2117.43401.50.65010054.10.1718.93601.80.61005076.70.2110.88020.61005094.30.2-17.66

图3　巴西实验及反演效果

反演效果如图3(a)所示，不难发现，模型反演的细观参数精度并不理想，只有剪切强度的精度在80%以上，其他参数精度波动很大，均值(图中虚线)为61%，难以满足实际应用。通过分析，主要原因为巴西实验在严格的实验条件保证下才能为沿中径的受拉破坏[9]，对细观参数进行随意的组合后需要对相应的试验条件进行重新设置才能保证实验的成功进行，而这个过程既繁琐又耗时，忽略这个过程从而导致实验时大部分圆盘并没有从中心起裂，微裂隙也不是沿着直径轨迹发育，如图3(b～c)所示，因此，所获得的抗拉强度并非真实值，而是无效数据，神经网络没有能力对数据进行准确拟合。

图4　直接拉伸实验数值模型

3　基于直接拉伸实验的细观参数反演

基于上述巴西间接拉伸实验难以进行大量的实验进而提供数据进行神经网络训练和反演，为此，编制了颗粒流直接拉伸实验程序进行神经网络训练，图4为直接拉伸数值模型[10-11]，两侧颗粒为加载层，用高黏结参数与中间颗粒(岩石)黏结，圆柱体长为100mm，半径为50mm。

选取与进行巴西实验一致的神经网络训练样本(表1)、学习函数、神经元设置，训练效果见图5。

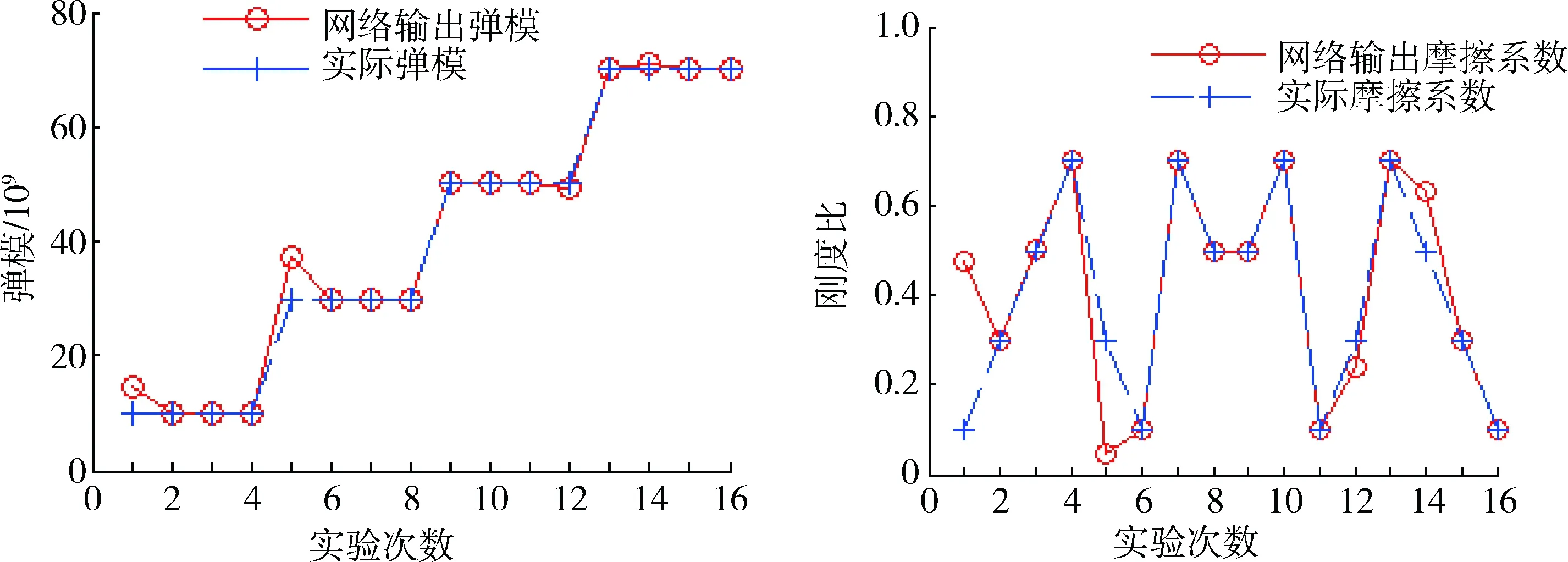
图5　直接拉伸下的神经网络训练效果

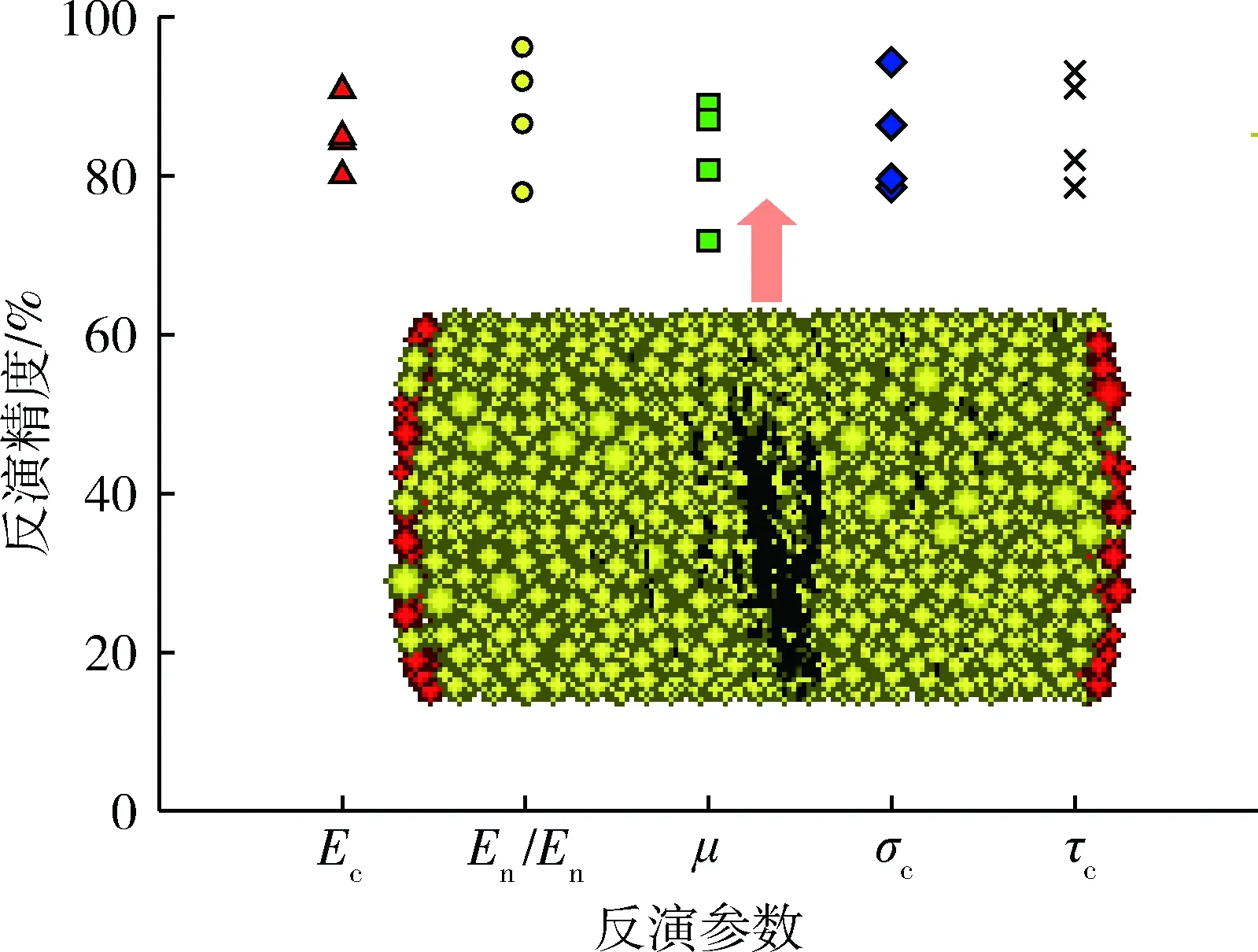
图6　直接拉伸实验反演效果

同样选取表2中四组样本进行反演和精度计算，反演效果见图6，可以看出网络反演精度较之前基于巴西实验数据训练的神经网络大幅提高，精度平均值为83%，表明直接拉伸实验提供的宏细观参数数据可靠性优于巴西实验提供的参数数据。事实上，在进行直接拉伸实验时，不同细观参数的数值模型破坏基本上都是沿模型中面受拉破坏，实验稳定性和数据稳定性大为改观，因此，直接拉伸实验可以提供本质上更为规律的样本供神经网络学习、训练，提高神经网络的准确性和可靠性，对细观参数的反演精度也就随之提高并更为可靠。

4　结　论

通过对颗粒流岩石试件分别进行巴西间接拉伸实验和直接拉伸两种实验，测定试件的抗拉强度，结合BP神经网络进行细观参数反演，对比两种实验，主要得到以下几点结论。

1)巴西实验条件苛刻，正交实验设计的任意参数颗粒流岩石试件受载后的破坏形式并非标准的沿中径受拉破坏，导致提供给神经网络学习、训练的样本属于本质无规律数据。因此，对于需要进行大量实验进行参数标定的颗粒流程序，不适于采用巴西实验进行岩石试件的抗拉强度标定。

2)直接拉伸实验简单、测试准确，对于任意参数颗粒流岩石试件均可以保证为中面受拉破坏，保证了BP神经网络学习的样本的数量和质量，进而提高了神经网络的训练效果和反演精度，因此，标定颗粒流岩石试件的抗拉强度应优先采用直接拉伸试验。

3)BP神经网络作为人工智能的重要手段，在保证样本质量的前提下，通过设置最优的网络参数(算法和神经元)，可以实现宏观多参数对细观多参数的高精度映射，是进行颗粒流岩石试件参数标定的有效手段。

4)对于实际应用，有两点建议：① 结合正交实验并适度增加训练样本，有利于提高神经网络的可靠性和反演精度；② 进行多种力学实验，测定岩石试件的弹性模量、泊松比、抗压、抗拉强度、黏聚力和内摩擦角，对神经网络进行系统训练和反演，实现对真实岩石参数向数值模型的全面映射。

[1]徐小敏，凌道盛，陈云敏，等.基于线性接触模型的颗粒材料细-宏观弹性常数相关关系研究[J].岩土工程学报，2010(7)：991-998.

[2]赵国彦，戴兵，马驰.平行黏结模型中细观参数对宏观特性影响研究[J].岩石力学与工程学报，2012(7)：1491-1498.

[3]周博，汪华斌，赵文锋，等.黏性材料细观与宏观力学参数相关性研究[J].岩土力学，2012(10)：3171-3175.

[4]尹成薇，梁冰，姜利国.基于颗粒流方法的砂土宏-细观参数关系分析[J].煤炭学报，2011(S2)：264-267.

[5]周喻，吴顺川，焦建津，等.基于BP神经网络的岩土体细观力学参数研究[J].岩土力学，2011(12)：3821-3826.

[6]周梅，刘松，王海超，等.利用神经网络预测混凝土的抗压强度[J].辽宁工程技术大学学报：自然科学版，1998(3)：275-277.

[7]韩力群.人工神经网络教程[M].北京：北京邮电大学出版社，2006.

[8]郭金敏，朱伶俐.煤矸石混凝土耐久性的正交试验研究[J].辽宁工程技术大学学报：自然科学版，2011(4)：566-570.

[9]庞海燕，李明，温茂萍，等.PBX巴西试验与直接拉伸试验的比较[J].火炸药学报，2011(1)：42-44.

[10]PotyondyD.O.，CundallP.A.Abonded-particlemodelforrock[J].InternationalJournalofRockMechanicsandMiningSciences，2004，41(8)：1329-1364.

[11]ChoN.，MartinC.D.，SegoD.C.Aclumpedparticlemodelforrock[J].InternationalJournalofRockMechanicsandMiningSciences，2007，44(7)：997-1010.

Microscopicparameterinversionofparticleflowrockbytwotensiletests

PANRui-kai1，ZHANGKai-zhi2，WANGShu-li1，JISong-tao1

(1.CollegeofMiningandSafetyEngineering，ShandongUniversityofScienceandTechnology，Qingdao266590，China；2.InstituteofMiningEngineering,GuizhouInstituteofTechnology，Guiyang550003，China)

Theaccurateparameterscalibrationofrockspecimenisthepreconditionsforapplyingtheparticleflowprogramtotheresolutionofactualengineeringproblems，andtensilestrengthisoneoftheparameters.Thispaperpresentsastudyontheaccurateandefficientbackanalysisofmicroscopicparametersofparticleflowrock，bycomparingandanalyzingtheBraziliantestanddirecttensiletestandincombinationwiththeneuralnetworkwhichpossessestheabilityofnon-linearmapping.Theconclusionsareasfollows：Braziliantest，whosebackanalysisaccuracyisonly61%，cannotguaranteethesuccessfuloperationsofthenumeroustests，andalsocannotprovidehigh-qualitysamplesfortheneuralnetworkasaresultofitsdemandingrequirements；Directtensiletest，whichishighlyadaptableandhasabackanalysisaccuracyof81%，canensurethequantityandqualityofthesamplesfortheneuralnetwork；BPneuralnetworkhastheabilityofmappingthemacroandmicroparametersaccuratelyonconditionthatthequantityandqualityareguaranteed，whichindicatesthatitisaneffectivemethodfortheparameterscalibrationofparticleflowrockmaterial.

directtension；artificialneuralnetworks；microscopicparameterinversion；Braziliantest；particleflowcode；discreteelementmethod

2016-12-28

国家自然科学基金项目资助(编号：51564004，51374139)；贵州省科技厅、贵州理工学院联合基金项目资助(编号：〔2014〕7370)；山东省自然科学基金项目资助(编号：ZR2013EEM018)

潘瑞凯(1990-)，男，山西晋中人，硕士研究生。E-mail：panrk001@163.com

张开智(1965-)，男，重庆人，教授、博士生导师。E-mail：zkzhi82@163.com。

TU458+.3

A

1004-4051(2016)08-0143-04