利用摄影基线改进SIFT算法

2016-09-08崔建军李亚东张晓栋张韶华范冬娟

测绘通报 2016年8期

关键词：航空摄影同名基线

崔建军，李亚东，张晓栋，罗　想，张韶华，范冬娟

(1. 长安大学地质工程与测绘学院，陕西西安 710054； 2. 解放军信息工程大学测绘学院，河南郑州 450052； 3. 73608部队，江苏南京 210028)

利用摄影基线改进SIFT算法

崔建军1，李亚东1，张晓栋1，罗想1，张韶华2,3，范冬娟3

(1. 长安大学地质工程与测绘学院，陕西西安 710054； 2. 解放军信息工程大学测绘学院，河南郑州 450052； 3. 73608部队，江苏南京 210028)

影像匹配是利用航空影像获取同名点和DEM的关键技术之一，而大倾斜影像的匹配问题也是目前匹配技术发展的难点。针对这一问题，本文研究了SIFT和ASIFT算法，并基于航空影像之间的摄影基线对ASIFT算法进行了改进，在成像模型中加入倾斜角度和平移变量，在一定程度上解决了大倾斜航空影像的自动匹配问题，并给出了试验结果。

影像匹配；同名点；ASIFT；航空摄影基线；成像模型

随着国民经济和遥感技术的发展，由于无人机遥感平台具有成本低廉、机动灵活、快速响应、能够承担高风险航空摄影任务和获取高分辨率影像等优点，其应用已经逐渐渗透到民用领域的各个方面。与之相应的，如何对无人机获取的遥感影像进行处理，从中提取有效的信息数据也得到越来越多的研究。近年来，利用SIFT算法进行影像匹配的研究得到越来越多的重视，因为其具有一定的仿射不变性[1-3]，也逐渐在无人机影像上得到了应用[4-7]。但是由于无人机遥感平台体积和重量都比较小，极易受到气流影响，导致其姿态很不稳定，影像的倾斜较大，此时SIFT方法也难以取得好的效果。针对这一问题对SIFT算法进行了深入的研究，并分析了图像变形产生的主要原因，从构像方程入手，在图像匹配过程中考虑相机姿态引起的图像变形，进而改进了SIFT算法。

一、Base-ASIFT

针对SIFT算法的局限性把相机姿态的变化引入到算法中，根据成像方程对图像进行重采样，尽可能恢复两张倾斜图像之间的可推导关系，进而改进了SIFT算法的匹配流程，最终实现了具有较大倾斜的两幅图像之间良好的匹配效果。

1. 相机的姿态

所谓相机姿态指的是相机在对目标进行成像时的位置、转角等参数值。通常情况下，相机获取目标的影像主要有两种形式：一是相机在以被拍摄对象为球心，拍摄距离为半径的球面上运动获取影像，这种情况通常出现在一般的对地面景物进行拍摄的过程中，如图1所示；二是相机沿着某一基线进行移动以获取目标的影像，这种情况通常出现在航空摄影或地面近景摄影等专业处理过程中，如图2所示。

图1　相机围绕被拍摄对象移动

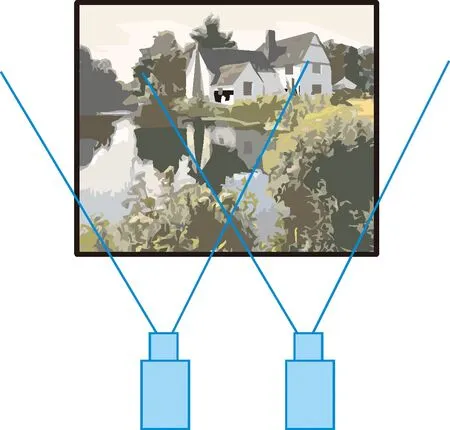
图2　相机沿某一基线移动

不论是哪一种情况，对每一次成像的过程可以表示为[8]

u=S1G1ATu0

(1)

式中，u表示经过成像的数字图像；而u0表示被拍摄对象的一个正面视图；T和A分别表示由于相机移动而产生的平面位移和仿射投影；G1表示高斯卷积，反映了光学模糊过程；S1表示位于一个规则格网上的标准采样算子。

2. 算法描述

针对图1所示的情况，Jean-MichelMorel等给出了详细的解决方案[8]，即以式(1)表示的成像模型为基础，把待匹配的两幅影像分别看成是相机在以被摄目标为中心、摄影距离为半径的球面上的成像，这样就可以通过球面极坐标的两个角度(θ,φ)和相机自身的旋转角度ω来确定相机成像时的倾斜矩阵A(实际上也就是相机成像时的旋转矩阵)，即

A=HγR1(ω)TtR2(φ)=

(2)

文献[8]中即以该式为基础，把两幅图像分别按照一定的间隔对θ、φ、ω3个角度进行循环，对于每一组角度利用式(1)得到倾斜后的图像，并对这一系列图像两两组合进行匹配，最后统计匹配成功的同名点。

ASIFT算法能够很好地处理一般的大倾斜影像，但对于两幅沿着某一条基线获取的航空影像对，由于其平移和旋转的情况都不同于一般的倾斜影像对，因此简单采用ASIFT算法也不能取得很好的效果，本文借鉴文献[8]的思路，针对图2的情况对式(2)和整个计算流程进行了修改。

(1) 旋转

航空摄影的处理过程中，相机的旋转是围绕着像主点和主光轴进行的，如图3所示。其中，θ、φ、ω3个角度都是像方角度[9]，而ASIFT算法中的旋转角度是物方角度，如图4所示。

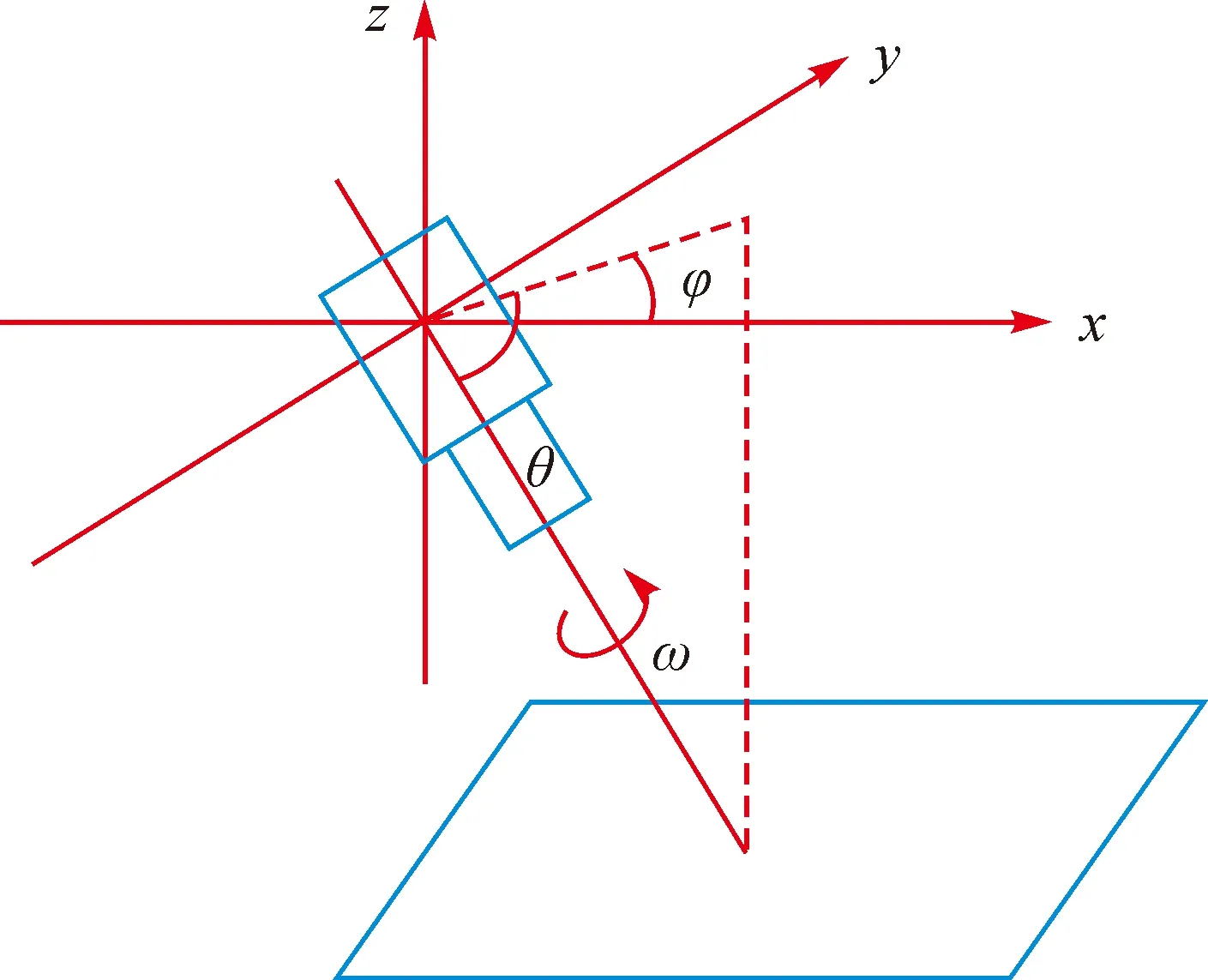
图3　航空摄影的相机旋转

图4　ASIFT中的倾斜角

因此如果要引用式(2)来推算倾斜影像，就必须把像方角度转换到物方角度，根据图3和图4的比较，可以得到计算式如下

(3)

将式(3)代入式(2)，则可以得到

(4)

其中

(2) 平移

航空影像是按照某一条基线获取的序列影像，这与一般的影像对不同，如图5所示。

图5　航空影像对之间的关系

图5中S1的坐标为(X1,Y1)；S2的坐标为(X2,Y2)，则存在如下的平移公式

将其转换为极坐标方程

式中，L为基线的长度；α为基线与左像空间(S1处获取的影像空间)坐标系中X轴的夹角。对于两幅图像而言，设在S1处获取的影像为F(x，y)，S2处获取的影像为F′(x′,y′)。则有

F′(x′+y′)=F(x+L·cosα,y+L·sinα)

(5)

根据式(4)和式(5)，式(1)的成像模型可以修改为如下的形式

u′=S1G1A′Tu0(x+L·cosα,y+L·sinα)

(6)

式中，A′根据式(4)产生。式(6)为修改后的成像模型。图6为根据修改后的成像模型对两幅影像进行匹配的流程。

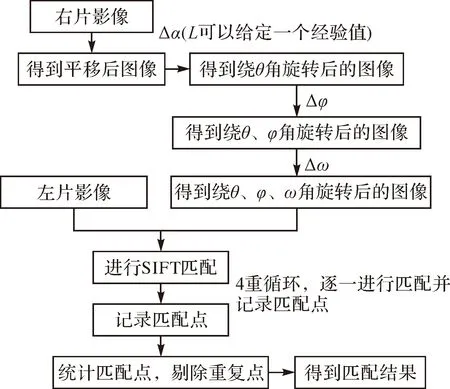
图6　Base-SIFT方法匹配流程

二、试　验

分别采用SIFT、ASIFT、Base-ASIFT这3种算法对一些在不同角度拍摄、具有较大倾斜的图像进行了试验并作了比较。图7显示了分别用3种算法进行试验的情况，其中白点代表匹配的同名点。

在这个试验中，虽然采用SIFT算法也匹配了318个同名点，但这些点都是错误的，ASIFT 算法得到了825个同名点，和Base-ASIFT算法相差不多，但其正确率却明显低于Base-ASIFT算法(见表1)。

表1　试验结果

图7　3种算法的匹配结果比较

试验结果显示,对于倾斜航空影像来说，Base-ASIFT算法能够得到更好的匹配结果，但其匹配速度和效率还有待于进一步提高。

三、结束语

本文针对航空影像的特点，在ASIFT算法的基础上加入基线平移变量，并按照航空摄影的相机姿态情况修改了ASIFT中的倾斜矩阵，然后以一幅图像为基准，与另一幅经过重采样后的一系列影像分别进行匹配计算，最后得到两张倾斜较大的航空影像上的同名像点。试验表明该算法比ASIFT方法更能适应航空影像的处理需求，能较好地解决大倾斜图像之间的匹配问题，对无人机影像的处理具有一定的价值。此外，该算法需要对一批模拟影像分别进行SIFT计算，因此运算速度较慢，虽然在采用SURF算法后速度有所提高，但如果要满足数据实时处理的要求，还需要进一步提高算法的计算效率。

[1]LOWEDG.DistinctiveImageFeaturesfromScale-invariantKeypoints[J].InternationalJournalofComputerVision(IJCV),2004, 60(2):91-110.

[2]LUOJuan,GWUNAO.ComparisonofSIFT,PCA-SIFTandSURF[J].InternationalJournalofImageProcessing(IJIP),2010, 3(4)：143-152.

[3]于丽莉，戴青.一种改进的特征匹配算法[J].计算机工程,2011,37(2):210-212.

[4]何敬,李永树,鲁恒，等.基于特征点的无人机影像拼接方法研究[J].光电工程,2011, 38(2):122-126.

[5]宫阿都,何孝莹,雷添杰，等.无控制点数据的无人机影像快速处理[J].地球信息科学学报, 2010, 12(2):254-259.

[6]何孝莹,岳建伟,张栩然.基于算法的无人机影像快速匹配[J].计算机工程,2011, 37(7):216-218.

[7]陈裕.基于SIFT算法的无人机遥感图像配准[D].长沙：中南大学, 2009.

[8]MOREL J M,YU G S.ASIFT: A New Framework for Fully Affine Invariant Image Comparison.[J].SIAM Journal on Imaging Sciences, 2009, 2(2):438-469.

[9]刘静宇.航空摄影测量学[M].北京：解放军出版社, 1995.

An Improved SIFT Algorithm Based on Photography Baseline

CUI Jianjun，LI Yadong，ZHANG Xiaodong，LUO Xiang，ZHANG Shaohua，FAN Dongjuan

2015-07-24；