VLBI观测对于CE-3着陆器定位和月球天平动参数的改进
2016-09-08魏二虎李智强董翠军刘经南金双根
魏二虎,李智强,董翠军,刘经南,金双根
(1. 武汉大学测绘学院,湖北 武汉 430079; 2. 立得空间信息技术股份有限公司,湖北 武汉 430223;3. 武汉大学卫星导航定位技术研究中心,湖北 武汉 430079; 4. 中国科学院上海天文台,上海 200030)
VLBI观测对于CE-3着陆器定位和月球天平动参数的改进
魏二虎1,李智强2,董翠军1,刘经南3,金双根4
(1. 武汉大学测绘学院,湖北 武汉 430079; 2. 立得空间信息技术股份有限公司,湖北 武汉 430223;3. 武汉大学卫星导航定位技术研究中心,湖北 武汉 430079; 4. 中国科学院上海天文台,上海 200030)
月球天平动参数是采用地面对“嫦娥三号”(CE-3)着陆器VLBI观测量确定其位置的必要参数。目前,获取天平动参数主要通过星表外推方式,导致天平动参数的外推精度和可靠性降低,从而降低了CE-3着陆器的定位精度。本文基于VLBI对CE-3的观测量,顾及月球坐标系的建立和连接问题,推导了同时解算月球天平动欧拉角参数和CE-3号位置参数的数学模型。利用我国VLBI观测网(CVN)实测数据对CE-3着陆器的定位参数和对月球天平动进行了解算。试验结果的分析表明,本文所推导的数学模型能够达到较好效果,提高了着陆器定位精度和改进了月球天平动参数。
嫦娥三号;VLBI;单点定位;月球天平动
本文的主要研究工作是在我国嫦娥探月项目二期工程“嫦娥三号”(CE-3)项目成功登月的背景下提出的。对于探月工程,获得着陆器准确位置意义重大。另外,月球天平动是月球真实存在的空间摆动,是描述月球重要的物理参数,是采用地面对(CE-3)着陆器VLBI观测量确定其位置时月球坐标系相互转换的必要参数,它还将以月球非球形引力位的形式作用于月球卫星轨道,对月球卫星的轨道产生摄动,对月球探测器轨道确定带来影响。现阶段月球天平动信息主要由(谁通过)LLR进行观测并由月球星历形式给出,如本文中使用的DE421历表采用了从1970—2007年共37年的LLR数据。对于2007年以后的天平动参数,则要通过星表内插外推的方式获取[1],这在一定程度上降低了天平动参数的精度和可靠性。通过确定着陆器在月固坐标系下位置的同时解算天平动,有助于提高天平动参数解算的精度和可靠性,对后续探月工程具有一定的借鉴意义。
笔者在文献[2]中利用SBI技术模拟计算了月球巡视器月面轨迹,取得了较好定位效果。徐焕宇等利用计算机视觉的方法计算月球着陆器位置,提出了利用图像序列进而完成对月球着陆器位置计算的方法[3]。黄勇等还利用多项式来表征着陆器在动力学着陆过程中的下降轨迹,采用统计定位方法计算着陆器动力下降轨道末端,还利用差分VLBI进行了巡视器和着陆器的相对定位[4]。曹建峰等对“嫦娥三号”着陆器的定位精度从跟踪弧段和测量数据组合两个方面进行了分析[5]。
综上所述,众多学者对月球着陆器的定位开展了大量的工作,但是前人在研究中较少涉及月球坐标系精确确立和连接问题,即进行天平动欧拉角的解算。在此背景下,开展VLBI月球着陆器定位及月球天平动欧拉角解算的研究有一定实际意义。
一、利用VLBI观测量确定CE-3着陆器位置和天平动参数的模型建立
1. 观测方程的建立

利用VLBI技术进行单点定位,其基本原理如图1所示,由图1可知
(1)
对有限源信号方向矢量可表述为
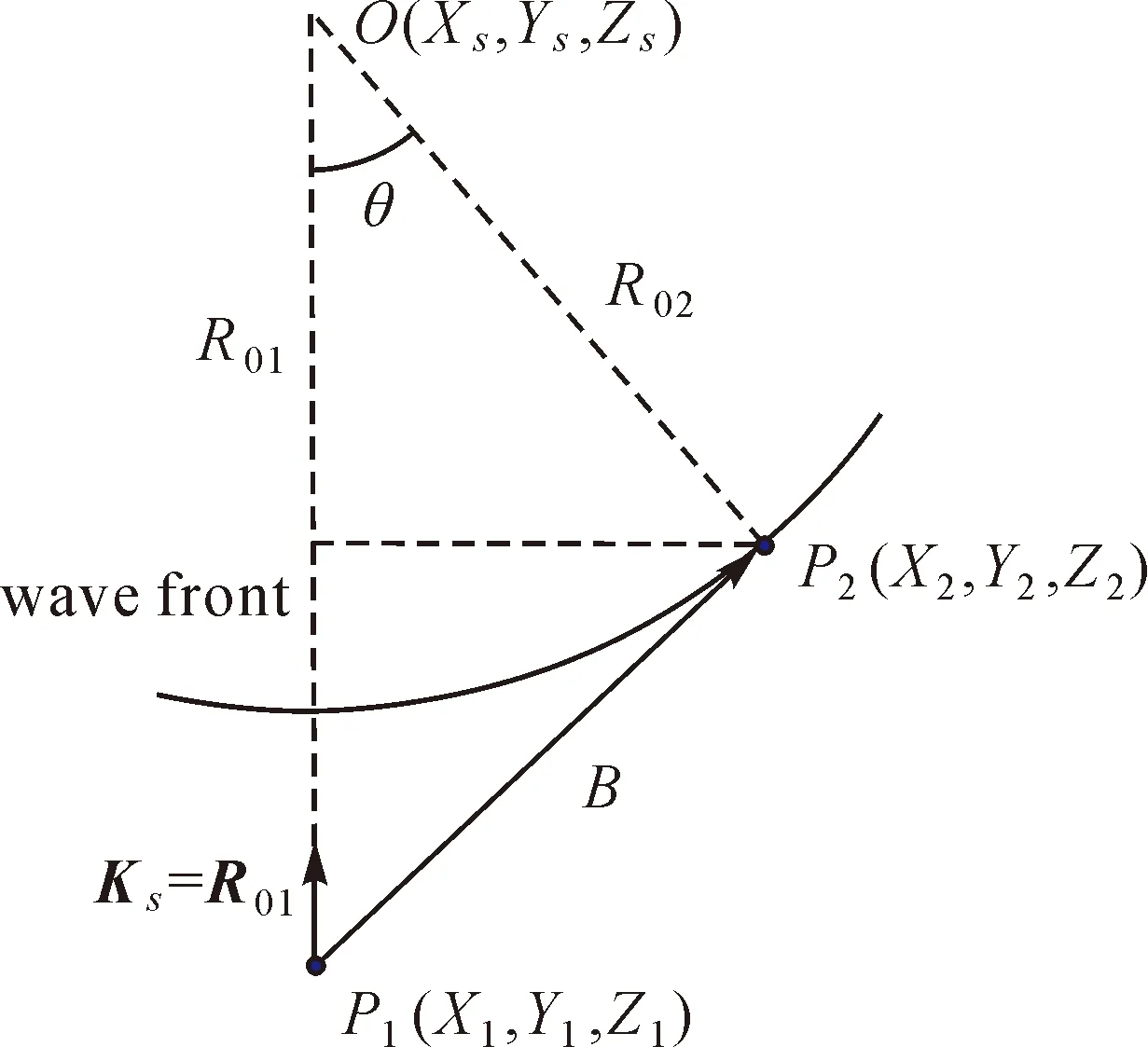
图1 VLBI单点定位示意图
(2)
此时,时延量可以表述为
R01-R02=Ks·B-R02(1-cosθ)
(3)
其中

(4)
本文重点考察“嫦娥三号”月球探测器3个位置参数以及对应时刻对月球天平动3个欧拉角的改正,故可将模型中其余参数视为已知量。顾及如下随机模型
(5)
但是,在“嫦娥三号”月球着陆器位置解算过程中,天平动欧拉角相较于位置参数而言量级很小,因此直接进行平差解算将会出现因法方程病态而导致的参数无法求解或解算精度极差的情况。为了解决此问题,本文采用参数加权平差的方法进行未知参数解算。
基于上述分析,将误差方程改写为
(6)
在最小二乘准则下,可得平差法方程[8]
(7)

(8)
观测值方差为
(9)
式中,r表示多余观测数。
下面将着重推导数学模型的线性化,令
(10)
v=B1dXS+B2dYS+B3dZS+B4dΩ+B5di+B6dμ-l
(11)
考虑某一观测历元,地面4个VLBI观测台站可以构成6条VLBI基线,也即能够得到6个观测值。对于此类观测方程,观测值对参数的偏导就是系数矩阵。时延对于位置的偏导数B1、B2、B3通过式(3)得到,其推导过程比较常见[2],此处略去。而天平动参数估计的文献很少,其偏导数B4、B5、B6推导叙述如下。
2. 天平动欧拉角偏导数
由观测方程可知,天平动是以月心月固到月心天球坐标转换过程中旋转矩阵的形式参与到解算当中,即RM。根据式(4)可得
(12)
此时,天平动欧拉角偏导数B4、B5、B6可分别表示为
(13)
(14)
(15)
二、试验与初步结果
1. 试验数据
由数学模型式(3)可知,VLBI试验观测量中包含地面VLBI测站天线坐标、坐标转换过程中EOP分量、月球着陆器初始坐标。下面具体介绍本文所涉及的数据。
1)VLBI数据。本文所使用信号时延数据为CVN实测数据,包括4个地面VLBI天线共6条基线对“嫦娥三号”着陆器着陆后的时延数据。所选取的弧段为:2013年12月20日19:41:57.439 125—20:48:32.439 156,共计4800个观测数据。
2)EOP参数。本文所采用的EOP参数为EOP(IERS)08C04序列。
3)JPL星历。本文采用了DE421进行数据解算。
4) 初始坐标。“嫦娥三号”探测器于2013年12月14日在月面进行软着陆,在此之前美国国家航空航天局(NationalAeronauticsandSpaceAdministration,NASA)的月球勘测轨道探测器LRO(LunarReconnaissanceOrbiter,50km轨道)曾对月球正面虹湾以东地区进行拍照,影像编号为M1127248516R。在着陆器着陆之后,12月25日,LRO再次飞过CE-3着陆点上方,拍摄影像编号为M1142582775R。经过图像处理,计算得出着陆器坐标为[8]

(16)
将上述经纬度代入月面数字高程模型得
H=-2636m
(17)
2. 初步结果与分析
为了验证在单点定位基础上解算天平动欧拉角是否可行,并分析解算天平动参数所带来的效果,本文设计如下试验。
由于VLBI具有极高的角分辨率,测量中对轨道的横向约束较强,而本文所采用的解算数据只有VLBI观测值,会导致径向(接近X方向)误差大于其他方向[9]。没有距离、速度观测值将对月球着陆器的解算带来很大的影响。因此将着陆器离月心距离作为约束条件,建立的限制条件方程如下
(18)
此处所采用的初始值的高程由月面数字高程模型获得,该模型空间分辨率为2.66km,高程中误差为120m。
通过求解参数的均方差来表示参数求解的精度,为了形象描述解算天平动参数所带来的效果,表1和表2表示的是每个历元求解位置参数及其均方差均值。

表1 位置参数解算结果 m
加入VLBI观测数据后,解算天平动与不解算天平动的着陆器坐标之间差值为1.4 m,与LRO给出的着陆器坐标差值分别为49和51 m,坐标变化较明显。

表2 位置参数均方差平均值
从表2中可以看出,X方向的残差均方差达到了百米级,明显大于其他两个方向,这是由于VLBI径向约束较弱。另外由数字高程模型所获取高程也有百米级的误差,虽然加入了高程方向的约束,在径向(接近X方向)误差依然较大。
由于Y、Z方向本身均方差量级较小,且规律相近,下面以X方向解算结果作为代表阐述问题。图2中,图例“是”表示解算天平动参数,“否”表示没有解算该参数。

图2 X解算结果
由上述试验结果可以看出,解算天平动参数可以减小位置参数均方差均值大小,X方向位置参数均方差均值减小37.8%,Y方向减小37.5%,Z方向减小37.5%,均方差越小,表示求解结果可信度越高。同时还可以看出,解算天平动参数之后,位置参数的稳定性更好,因此可以认为在对着陆器单点定位过程中解算天平动欧拉角参数可以提高位置参数的解算精度。
与章动极移类似,天平动是一个缓慢变化的物理量,为此本文解算了所有实测数据的天平动欧拉角参数,还引入俄罗斯EPM2011星历作为外部比较值,其结果如图3—图5所示。
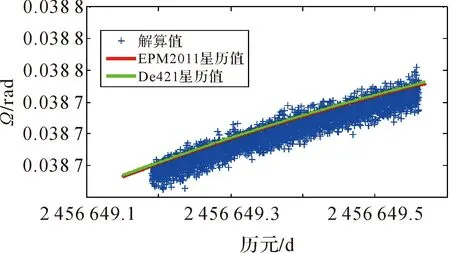
图3 Ω解算值

图4 i解算值
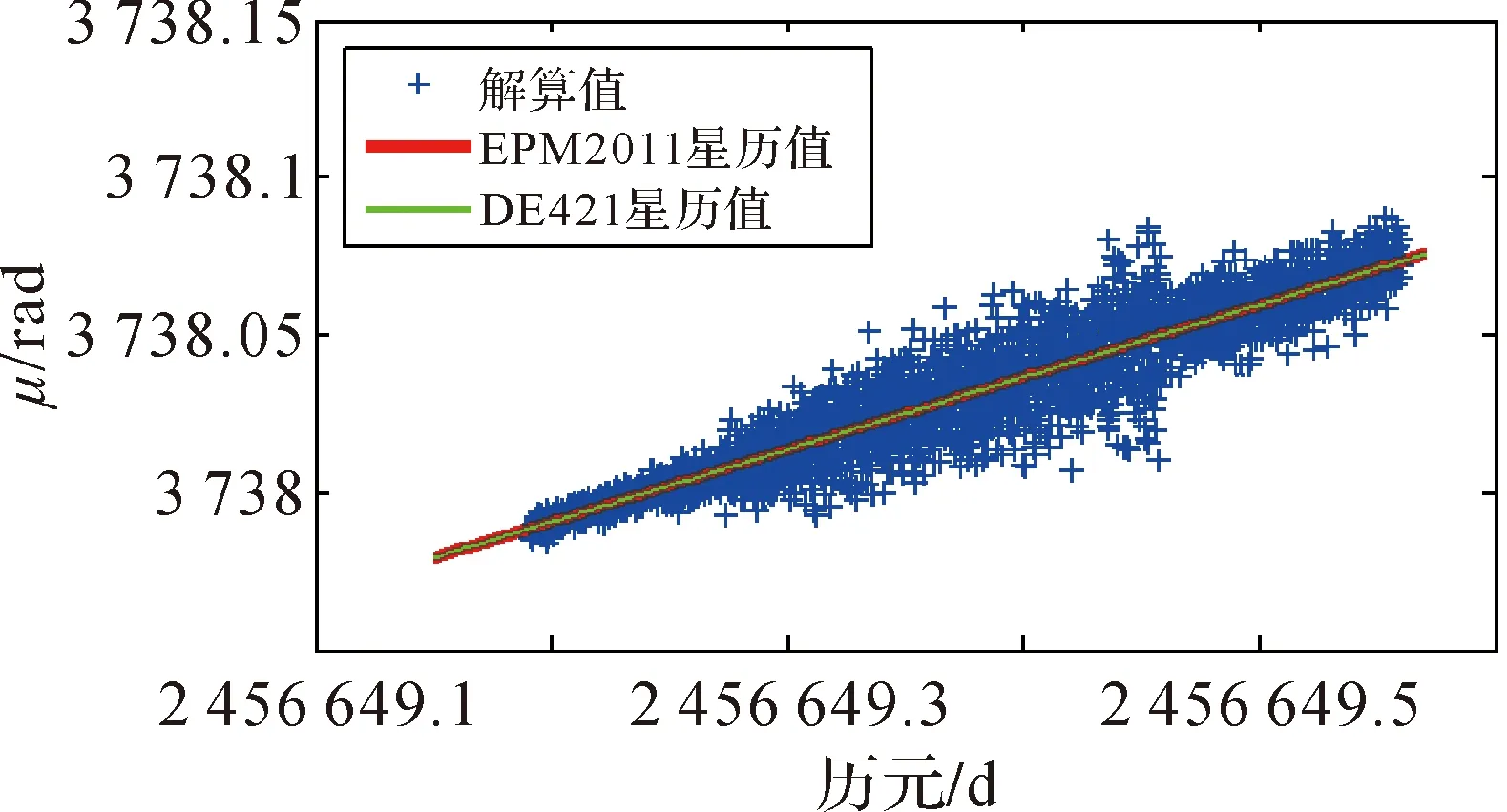
图5 μ解算值
由图3—图5中可以看出,除参数Ω以外,i、μ的解算结果均是围绕在星历所给出的数值周围波动,也即星历值为解算值的期望;对于Ω,由图3可以发现,解算值与星历值存在一个整体偏差,约为-0.000 004 rad。
究其原因,Ω表示的是月心指向春分点方向与月球赤道面交地球赤道面交线方向的夹角,在坐标转换中对横向方向起的作用较大,同时由于VLBI的高横向分辨率,故而能够对Ω进行改进。
为了验证解证天平动欧拉角参数改进的意义与贡献,本文设计了一组对比试验,试验条件为:单历元解算着陆器位置参数,其中一个试验采用DE421星历,对比试验采用DE421星历的Ω加上整体偏差-0.000 004 rad,其他条件一致,得到结果如图6所示。
位置参数解算方差统计结果见表3。

图6 采用Ω改进值X对比

由图6和表3中的结果可以发现,当使用改进值进行着陆器位置解算时,位置参数解算结果的方差变小。KM-SH基线残差如图7所示。

图7 KM-SH残差对比
由文献[6]可知,VLBI能以厘米级甚至毫米级的精度测定相距几千千米的两个测站间的基线向量,相对精度可达10-8~10-9。图7中两种方法解得的KM-SH基线残差大部分小于1 cm,可知解算效果较好。并且可以看到,采用改进值解算后的KM-SH基线残差明显小于使用DE421星历的解算结果。
解算残差的大小在一定程度上表示模型的正确与否,综合位置参数解算结果和基线解算残差可以认为改进后的Ω值更加准确,因此在实际工程中应加以应用。
三、结束语
本文在利用地面对CE-3着陆器的VLBI观测量进行定位的基础上,顾及了月球坐标系的建立和连接问题,推导了月球天平动欧拉角参数解算数学模型。利用我国VLBI观测网(CVN)采集的“嫦娥三号”着陆器的实测数据,对月球天平动进行估计,有效地提高了星表外推得到的天平动参数精度和可靠性。通过试验进一步分析表明,在对月球着陆器进行单点定位时解算月球天平动能够提高着陆器定位精度,且利用VLBI实测数据,能够对月球天平动特别是Ω有较好的改进效果。随着观测数据的增加,利用长时间对天平动参数的计算改进,以期能够更加准确地描述天平动结果。
[1]邓雪梅,樊敏,谢懿. JPL行星历表的比较与评估[J]. 天文学报,2013,54(6):550-560.
[2]WEI Erhu, JIN Shuanggen, YANG Hongzhou, et al, Simulation and Results on Real-time Positioning of Chang’E-3 Rover with the Same-beam VLBI Observations[J]. Planetary and Space Science,2013(84):20-27.
[3]徐焕宇,刘佶鑫,孙巍巍,等. 基于序列图像的月球着陆定位计算方法研究[J]. 计算机科学,2011,38(12):269-273.
[4]黄勇.“嫦娥一号”探月飞行器的轨道计算研究[D]. 上海:中国科学院上海天文台,2006.
[5]曹建峰,胡松杰,张宇,等. 嫦娥三号着陆器统计定位精度分析[J]. 飞行器测控学报,2014, 33(3):244-249.
[6]李征航, 魏二虎, 王正涛,等. 空间大地测量学[M]. 武汉: 武汉大学出版社, 2010.
[7]SEKIDO M,FUKUSHIMA T. A VLBI Delay Model for Radio Sources at a Finite Distance[J]. Journal of Geodesy,2006, 80(3):137-149.
[8]National Aeronautics and Space Administration. Images of Chang’e 3 Landing Site[EB/OL].2013-12-30[2015-08-29].http:∥www.nasa.gov/content/nasa-images-of-change-3-landingsite/#.UtUDbtLUNP.
[9]黄勇,胡小工,黄珹,等. 利用VLBI数据确定“探测一号“卫星的轨道[J]. 天文学报, 2006, 47(1): 82-91.
[10]崔希璋, 於宗俦, 陶本藻,等. 广义测量平差[M]. 武汉: 武汉大学出版社, 2005.
[11]TAYLOR D B,BELL S A, HILTON J L, et al. Computation of the Quantities Describing the Lunar Librations in the Astronomical Almanac[EB/OL].[2015-08-30]. http:∥astro.ukho.gov.uk/data /tn/naotn74.pdf.
On the Improvement of Chang’E-3 Lander Position Determination and Lunar Librations Estimation with VLBI Observations
WEI Erhu,LI Zhiqiang,DONG Cuijun,LIU Jingnan,JIN Shuanggen
10.13474/j.cnki.11-2246.2016.0244.
2015-10-12
国家自然科学基金(41374012)
魏二虎(1965—),男,博士,教授,主要从事空间大地测量和地球动力学研究。E-mail:ehwei@sgg.whu.edu.cn
P228.6
B
0494-0911(2016)08-0001-05
引文格式:魏二虎,李智强,董翠军,等. VLBI观测对于CE-3着陆器定位和月球天平动参数的改进[J].测绘通报,2016(8):1-5.
