结合主题特征和互作用网络拓扑特性的关键蛋白质识别
2016-09-08邵明玉
崔 鑫 邵明玉
(复旦大学计算机科学技术学院 上海 200433)
结合主题特征和互作用网络拓扑特性的关键蛋白质识别
崔鑫邵明玉
(复旦大学计算机科学技术学院上海 200433)
关键蛋白质是生物体内维持生存和繁殖所必须的蛋白质。关键蛋白质的识别和预测不仅对我们理解维持生物生存的最小需求有重要意义,也在药物设计、药物靶标发现等领域有重要作用。已有的关键蛋白质识别算法大多基于蛋白质互作用网络中的拓扑特性,在识别算法中引入了一个新的特征,即考虑到关键蛋白质序列本身的主题分布特征。通过将LDA模型与基于蛋白质互作用网络拓扑特征的CPPK算法相结合,提出了新的识别算法: 结合主题模型和蛋白质互作用网络拓扑特性的关键蛋白质识别。该识别算法在酵母蛋白质数据集上测试,并与现有的若干关键蛋白质识别算法进行比较。实验表明,通过引入LDA模型以及新的特征来对原有的CPPK预测算法进行改进,达到了比之前更好的识别效果。
主题模型中心性测度蛋白质互作用网络关键蛋白质
0 引 言
蛋白质在每个有机生命体中担当着重要的角色,其中关键基因及其产物关键蛋白质对于有机体的存活及功能调控更是必不可少的。以往研究表明[1,2],缺少一个关键蛋白质就可能导致生命体的死亡或不育。Winzeler[1]等将关键蛋白质定义为通过基因剔除式突变将其移除后造成有关蛋白质复合物功能丧失。也正是由于关键蛋白质的这种不可或缺性,它逐渐成为新型抗生素药物的靶标。
研究人员在过去通过许多实验的方式寻找关键蛋白质,包括单基因敲除[3]、RNA推断[4]以及条件基因敲除[5]等。而利用生物实验的方法对关键蛋白质识别往往面临着价格昂贵及时间耗费的问题,实验人员不同的实验条件也影响着对关键蛋白质的识别。随着高通量技术的发展,蛋白质测序技术的提升,可获得的蛋白质相互作用数据和蛋白质序列数据日益丰富,研究者们将注意力转向通过计算的方式发现和预测关键蛋白质。在预测关键蛋白质的算法中,最重要的是寻找能充分表示关键蛋白质的特征。目前,通过计算的方式预测关键蛋白质的方法主要基于两类特征信息:蛋白质序列信息和蛋白质相互作用网拓扑结构[6]。蛋白质序列信息主要从进化的保守性、基因表达、蛋白质功能和调控方面描述了单个蛋白质的必要性,是个体蛋白质功能信息的最直接的描述。而细胞中每个蛋白质不是孤立存在,是通过与其他蛋白质一起相互作用组成复合物来行使其功能,所以蛋白质相互作用网络从某种程度上反映了单个蛋白质与其他蛋白质的复杂关系,进而表明个体蛋白质在复合物中的重要作用。
LDA模型[7]是近年来在文本挖掘领域中出现的一种概率模型,因为模型的概率统计基础可以对数据单元隐含关系进行挖掘,使其应用在生物概念标注[8]、基因表达模式识别[9]和蛋白质-蛋白质相互作用关系预测[10,11]等问题中,成为了生物数据领域中对信息挖掘和提取的有效统计方法之一。然而,目前还没有研究工作将主题信息引入关键蛋白质预测算法中。这里通过引入蛋白质序列的主题分布信息提出了新的关键蛋白质预测算法,TMNT(Topic model and network topology based method)。TMNT算法在现有的关键蛋白质预测方法(基于蛋白质相互作用网络拓扑结构的中心性测度)中引入蛋白质序列信息,利用LDA模型对蛋白质序列建模,定义了新的未知蛋白质与关键蛋白质间的加权相似度计算方法,从而在未知蛋白质数据中预测潜在关键蛋白质。预测算法在酵母蛋白质序列和相互作用网络数据集上进行测试,并与现有的若干关键蛋白质序列算法进行比较。实验表明:在ROC评测标准中,结合了蛋白质序列特征和网络拓扑信息的预测算法优于只采用网络拓扑结构的关键蛋白质预测算法,通过引入蛋白质序列的主题分布信息,新的关键蛋白质识别方法比原CPPK算法的识别精确度有所提高。引入主题信息的识别方法为关键蛋白质识别研究提供了新的途径。
1 计算模型及预测算法
1.1主题模型
主题模型是文本挖掘中的一种概率模型。以潜在狄利克雷分配LDA[7]模型为代表,演变出一系列概率主题模型,这些模型被推广应用于图像处理、情感分析、生物数据挖掘等信息处理领域。在本文中,利用LDA模型对蛋白质序列进行特征提取,将原来的生物序列映射到蛋白质功能模块空间(主题空间)。

图1 LDA图模型表示
LDA是一种层次贝叶斯模型,可以用概率图表示为图1所示。其中圆圈表示随机变量:空心圆圈表示不可被观测的变量,实心圆圈表示可以被观测到的变量,箭头表示变量之间的依赖关系,即条件概率中的变量依赖关系,矩形表示内部结构的重复,矩形右下角的角标表示重复的次数。在蛋白质序列数据中,每条序列被重新编码分割成氨基酸片段,这些片段被预处理映射到73(343)空间维度上。这样,每个蛋白质序列被表示为氨基酸片段,而这些片段来自于一个343维度的空间。在重新编码后的氨基酸片段上对LDA模型变量重新定义为:M为蛋白质数据集中包含蛋白质序列的个数,N为一条蛋白质序列中氨基酸片段的个数,T为预先定义的蛋白质功能调控模块的个数,w为某个已知(可观测)的氨基酸片段,z为当前氨基酸片段所属的功能调控模块,φ为特定功能模块下氨基酸片段的多项分布,θ为一条蛋白质序列在功能模块中的概率分布,α和β是贝叶斯模型的先验超参数。
基于LDA模型,我们假设一条蛋白质序列的生成过程如下:
1. 根据Dirichlet先验分布Dir(α)得到一条蛋白质序列d的功能模块(主题)分布θ。
2. 对于蛋白质序列d中的每个氨基酸片段w的产生:
a) 根据多项分布Mul(z|θ)采样一个功能模块(主题)z。
b) 根据功能模块z和功能模块下φ的多项分布Mul(w|z,φ)采样一个氨基酸片段w。
其中,θ表示了蛋白质序列到功能模块的分布,φ表示了在功能模块下氨基酸片段的多项分布。通过引入这个概率生成模型,为我们带来了两个好处:1)实现了蛋白质序列的低维表示(从原来的序列空间映射到功能模块空间);2)抽取了蛋白质序列集上以氨基酸片段为单位的功能模块的挖掘,即主题空间。
给定超参数α和β后,θ、z和w的联合分布为:
(1)
对连续变量θ和离散变量z分别积分求和,得到蛋白质序列向量w的边缘分布:
(2)
在这个概率图模型中,求解问题是一个非常复杂的最优化问题,这里我们用Gibbs采样的方法近似迭代求解[12]。Gibbs采样的基本思想是:给定一个多维变量的分布,相比于对于联合分布积分,从条件分布中采样更简单。假设要从一个联合分布概率p(x0,x1, …,xn)中获得K个样本X={x0,x1, …,xn}的两个步骤为:
1. 随机初始化每个变量获得X(0);
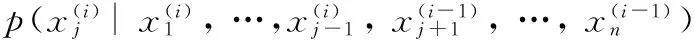
在基于LDA模型的Gibbs采样求解中,从公式(1)中变量的联合分布,可以推导出适合Gibbs采样的氨基酸片段w和功能模块(主题)T的全条件分布:
(3)
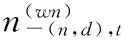
1.2网络拓扑结构
在蛋白质相互作用网络(简称蛋白质网络)中,结构与功能的相关性表现为蛋白质在生物功能上的重要性和其在对应节点所处拓扑位置之间的密切联系。Jeong[13]等在酵母蛋白质网络中发现,节点度数小于5的蛋白质集合中有21%是关键蛋白质,当度数大于15时,集合中包含关键蛋白质的比例上升为62%。这个研究结果表明,在蛋白质网络中拥有较多相邻节点的蛋白质的缺失更易于影响整个网络的拓扑结构,进而对生命体产生致死或无法繁衍的效应,而这一效应也符合对关键蛋白质的定义。
本文采用边聚类系数ECC(Edge Clustering Coefficient)[14]来计算蛋白质网络中两个节点的相关性。蛋白质网络可以被看作一个无向图G=(V,E),其中V表示蛋白质节点的集合,E表示蛋白质之间相互作用边的集合。对于连接节点u和v边E
(4)
其中zu,v表示在网络中包含边E
1.3预测算法
根据以上两个核心算法思想,将关键蛋白质预测算法的流程概括为图2所示。其中相似度计算是衡量算法模型最关键的步骤,这里,利用加权的蛋白质序列信息和蛋白质网络信息量化蛋白质之间的相似程度,蛋白质u和蛋白质v的相似度sim(u,v)定义为:
sim(u,v)=λ×ECC(u,v)+(1-λ)×
(1-DKL(u,v))
(5)
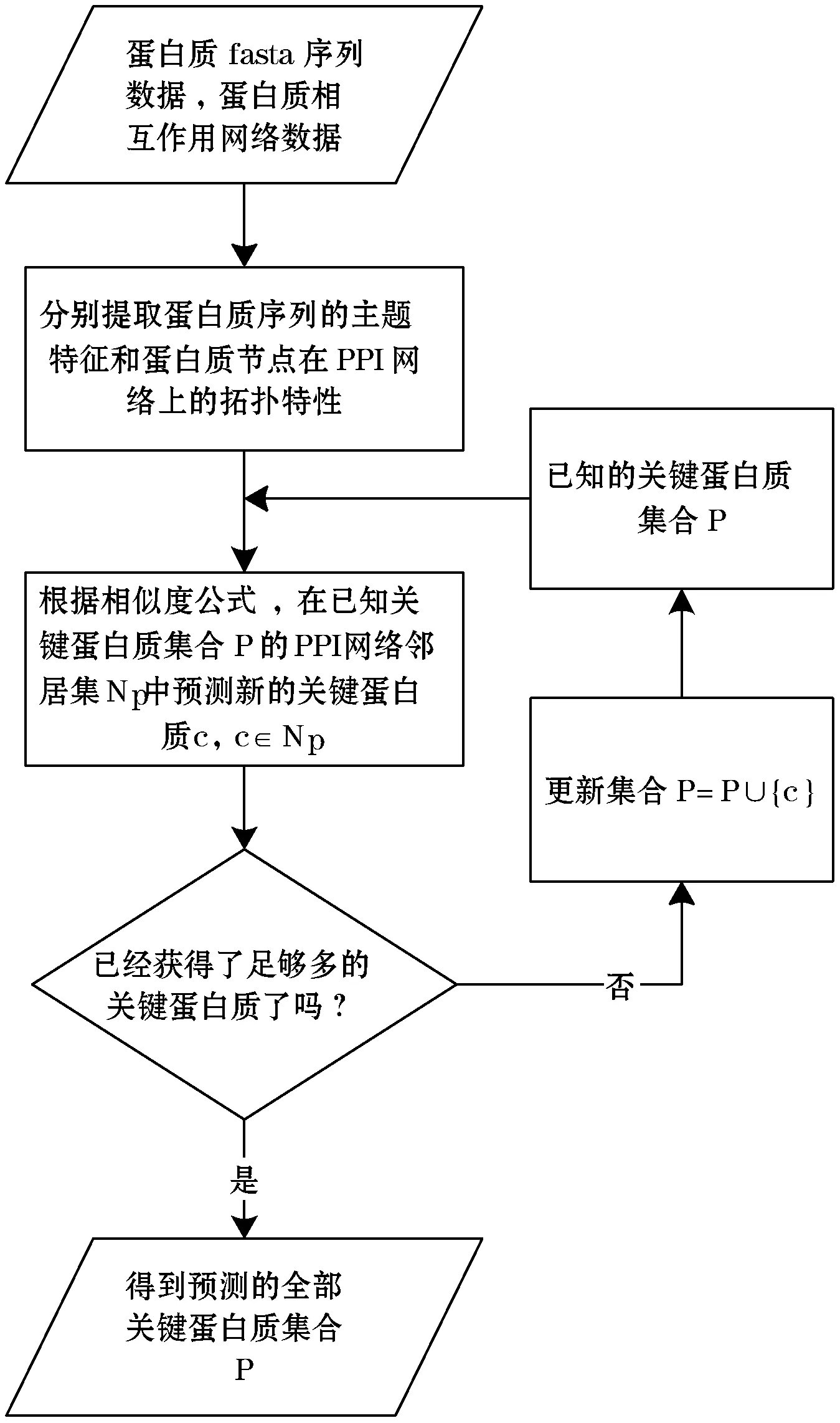
图2 关键蛋白质预测流程图
其中ECC(u,v)为蛋白质u和v在蛋白质互作用网络中的边聚类系数;DKL(u,v)为蛋白质u和蛋白质v在序列特征上的相对熵(又称为KL距离,Kullback-Leibler divergence),衡量了蛋白质序列主题分布的差异,这里采用了正规化后的KL距离;λ为调节蛋白质序列特征和PPI拓扑特性比重的参数,即取值在[0, 1]区间的权重系数。ECC(u,v)值越高,表示连接两个节点的边在网络的小模块结构中越倾向于中心地位。1-DKL(u,v)越大,表示蛋白质序列u和v的主题分布之间的KL距离越近,差异程度越小。因此,sim(u,v)值越大,蛋白质u和蛋白质v的重要程度越相似。每次选取与关键蛋白质集合p最相似的蛋白质为预测的关键蛋白质,并把预测的关键蛋白质加入到已知关键蛋白质集合:
(6)
p=p∪{u|max{p(u),u∈Np}}
(7)
其中Np为关键蛋白质集合p在蛋白质网络中所有邻居节点集合。算法的初始阶段,关键蛋白质集合p用均匀分布随机采样的方式从已知关键蛋白质集合中生成。
2 实验与结果分析
本文利用酵母的蛋白质序列数据和蛋白质相互作用网络来预测关键蛋白质,并对预测结果做出分析和评价。
2.1数据集及预处理
酵母的蛋白质数据集具有可靠性高,数据完备的特点,因此实验以酵母蛋白质数据集作为研究对象。其中,酵母蛋白质序列数据来自于S. cerevisiae strain S288C[18]。酵母蛋白质相互作用网络采用两个高可信数据库:DIP数据库[19]和BioGRID数据库[20]。
酵母序列数据包含6713条蛋白质序列。酵母蛋白质相互作用数据集在预处理过程中首先移除物种间相互作用,只保留物理相互作用。蛋白质相互作用数据集中,DIP数据库下载的蛋白质网络共包含4860个节点和22 138条相互作用边,BioGRID数据库下载的BIOGRID蛋白质网络包括5877个节点和84 686条相互作用边。关键蛋白质数据是通过整合以下四个数据库:MIPS[24]、SGD[25]、DEG[26]和SGDP[27]的数据而来,包含1274个关键蛋白质。
对于蛋白质序列的预处理过程,首先根据氨基酸的偶极子和侧链的体积特性,将20种基本氨基酸分成7类[10]。如表1所示,对于特殊氨基酸,例如X、B和U,分到第6类中。

表1 氨基酸分类
例如,一条蛋白质序列P的氨基酸残基片段为:
P=MVLTIYPD…
这里,每个字母表示氨基酸残基的字母符号。根据表1的分类规则,原始氨基酸残基替换为类别标签后为:
P=C3C1C2C3C2C3C2C6…
再将替换后的序列以长度为3的滑动窗口切割。这样,我们就得到了73(73=343)的片段空间,并且原始的每条蛋白质序列被分成若干片段组合。
2.2评价方法
为了评价算法在酵母数据集中的关键蛋白质预测性能,引入主题信息的关键蛋白质预测算法与2014年Min Li[21]等人提出的利用蛋白质网络中心性拓扑性质预测关键蛋白质的CPPK算法、新的中心性测度方法NC(New Centrality Measure)[14]及基于局部平均连接度的方法LAC(Local Average Connectivity based method)[22]进行横向比较。同时,对不同数目的功能模块(主题)以及不同的相似度权重λ的选取对预测算法结果的影响进行纵向分析比较。
本文采用文献[21]定义的预测算法精确度:
(8)
这里,预测方法Mi对预测结果集C的精确度为:预测结果集与真实集合Ve的交集在预测结果集中所占的比例。
同时,本文使用ROC(Receive Operating Characteristic)曲线和ROC曲线下的面积AUC值(Area Under Curve)两个指标来综合衡量预测算法。 在ROC曲线中,纵坐标为敏感度(Sensitivity)或真阳性率TPR(True Positive Rate),横坐标为特异性(Specificity)或真阴性率TNR(True Negative Rate):
在二分类模型中,TP表示真阳性,FP表示伪阳性,TN表示真阴性,FN表示伪阴性。ROC和AUC常被用来评价一个二值分类器的优劣,在ROC曲线中,计算不同的权重下预测结果的真阳性在假阳性中的比重。因此ROC曲线越靠近坐标系左上角,预测算法越好,同理AUC的值越大,预测算法准确率越高。
2.3实验结果分析
在酵母蛋白质序列数据集中一共包含6713条序列,其中1256条关键蛋白质,5457条其他蛋白质(包括非关键蛋白质和未知类型蛋白质)。可以看出,真实数据集中正样本(关键蛋白质)和负样本(其他蛋白质)比例不平衡。
在蛋白质序列数据集和PPI网络数据集上计算了主题数从20到100,步长为20,相似权重λ从0到1,步长为0.1的设定下,由100个已知的初始关键蛋白质从数据集中预测100个新的关键蛋白质的精确度,如表2所示为算法在DIP网络上的精确度。其中,当主题数目为20,λ为0.2时,预测算法的精确度最高,达到82%。算法在λ等于0.1和0.2时,预测精确度最高,平均分别为:71.8%和72.5%。并且根据精确度曲线走向可以看出,算法在不同主题数目和权重向量λ下,精确度保持平稳的趋势,虽然最低的精确度只有59.0%,但是由于数据集的不平衡(随机方法预测关键蛋白质的准确度为18.7%),在最差的预测结果下算法仍然可以选出一半的关键蛋白质。表3为算法在BIOGRID网络上的精确度。其中,当主题数目为40,λ为0.3时,预测算法的精确度最高达到73.5%。在BIOGRID网络上的整体精确度比DIP网络要差一些,分析原因可能是由于BIOGRID网络规模更大。由于预测使用的100个已知关键蛋白质和预测出的100个潜在关键蛋白质较网络5877个节点的数据规模差距很大,并且5877个蛋白质中最多只有1256条关键蛋白质。样本的不平衡性及预测数据整体的不均衡性,使得预测算法受网络规模影响,网络规模越大,预测算法准确率可能越低。
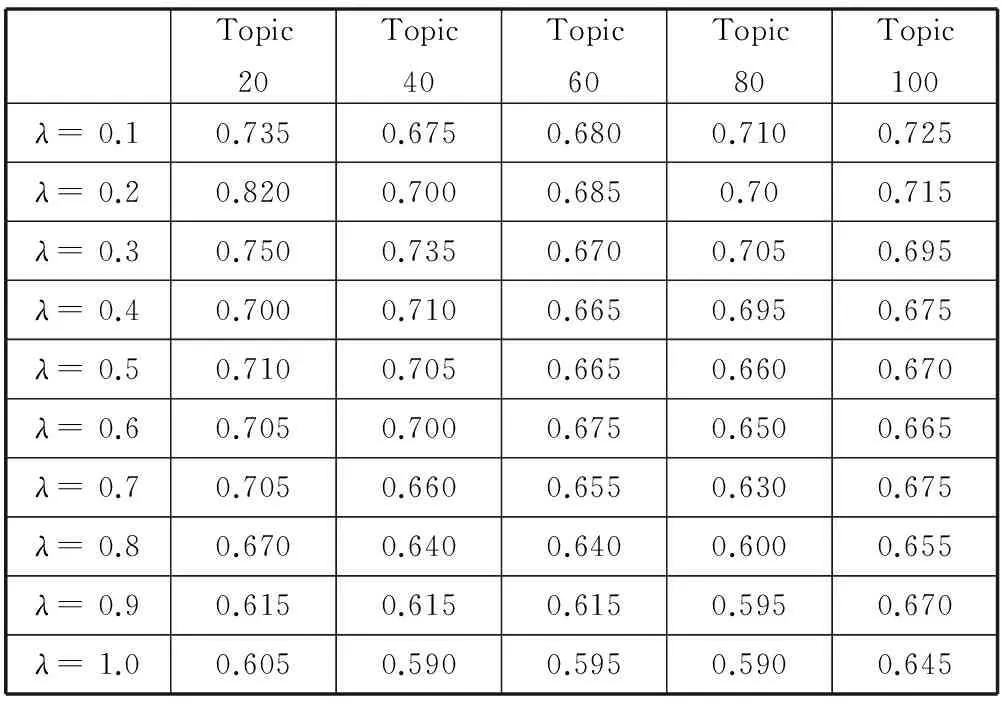
表2 DIP网络不同权重和主题数目下的预测精确度

表3 BIOGRID网络不同权重和主题数目下的预测精确度
其次,由于在计算相似度时加权结合了序列信息和网络拓扑信息,因此横向比较了单独使用序列信息(λ为0时,只采用主题模型信息)和单独使用网络拓扑信息(λ为1时,只采用CPPK网络中心度信息)时的预测精度。如图3所示,表示DIP网络上主题模型与网络拓扑的对比图,图4表示BIOGRID网络上主题模型与网络拓扑的对比图,其中横坐标为主题个数,纵坐标为预测精确度。不难看出,只利用蛋白质序列主题信息对关键蛋白质预测优于单纯使用CPPK算法的关键蛋白质预测算法。这里,在每组对比实验中,使用相同的初始化已知关键蛋白质种子集合,例如,在主题数目为10的Topic Model与CPPK算法初始化使用相同的已知关键蛋白质集合。对于不同组的实验中(主题数目不同的实验中),由于随机产生初始化已知关键蛋白质,所以不同组实验的初始化已知关键蛋白质集合不同。

图3 DIP网络主题模型信息与网络拓扑信息预测精确度
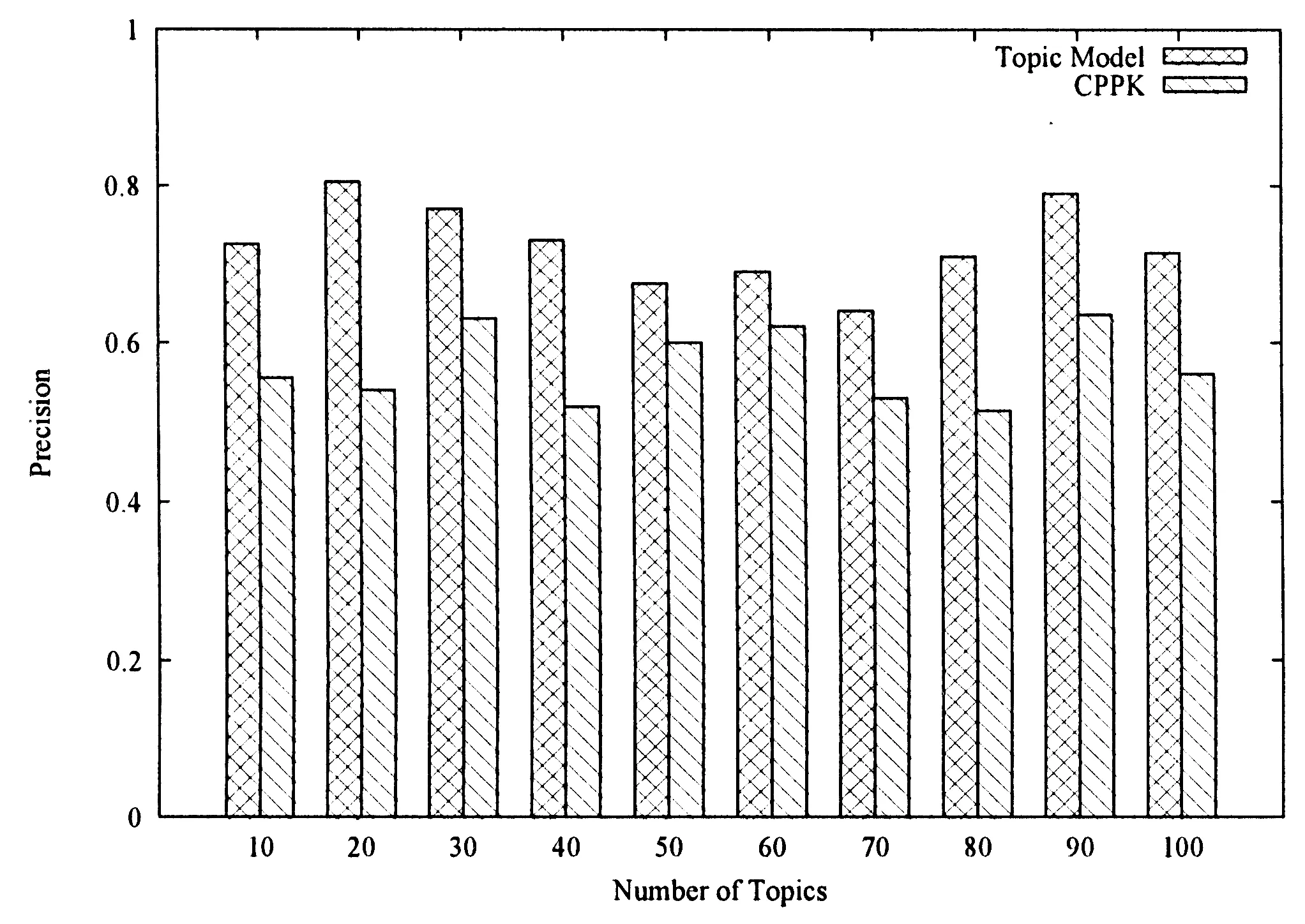
图4 BIOGRID网络主题模型与网络拓扑信息预测精确度
表4列举总结了在DIP网络中每个主题数目下最高的预测精确度及其对应的λ。根据表4的统计,我们发现在DIP网络中相似权重λ在不同主题下对精确度的影响基本稳定在[0.1,0.3]。表5列举了在BIOGRID网络中相似权重λ在不同主题下对精确度的影响基本稳定在[0.0, 0.3]区间内。由两个网络的统计结果看来,蛋白质的序列结构和网络拓扑信息的结合对关键蛋白质的预测精确度具有稳定比例。
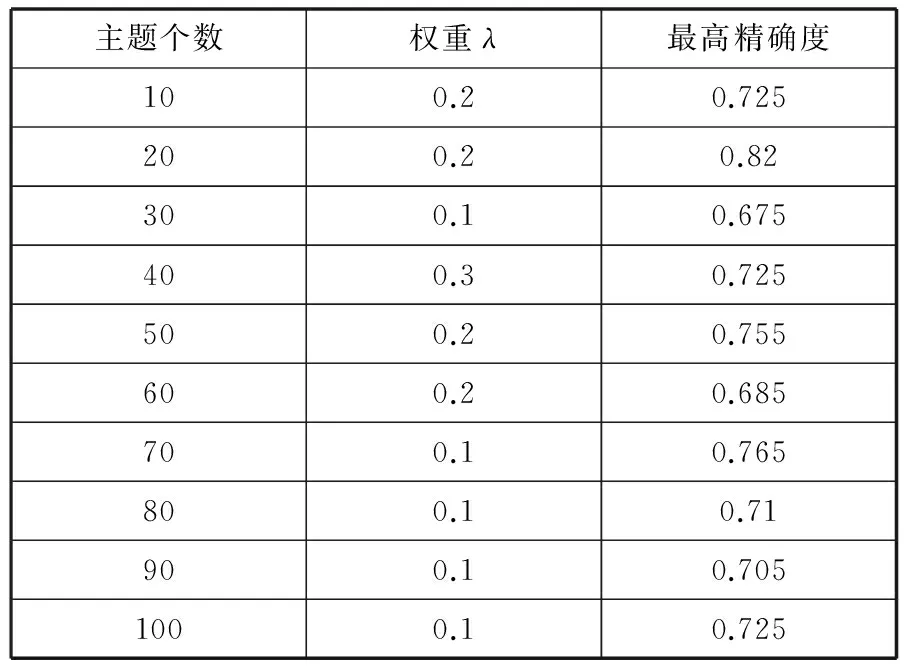
表4 DIP不同主题下最高预测精确度

表5 BIOGRID网络不同主题下最高预测精确度
本文将引入主题信息的改进的CPPK关键蛋白质预测算法:基于主题模型和网络拓扑结构的关键蛋白质预测算TMNT与原有的CPPK预测算法进行了比较。图5为两种算法在DIP蛋白质网络数据与蛋白质序列数据集上的精确度比较结果,图6为两个算法在BIOGRID蛋白质网络数据与蛋白质序列数据集上的精确度比较结果,其中TMNT算法的精确度选择每个主题下λ为0.2对应的精确度。
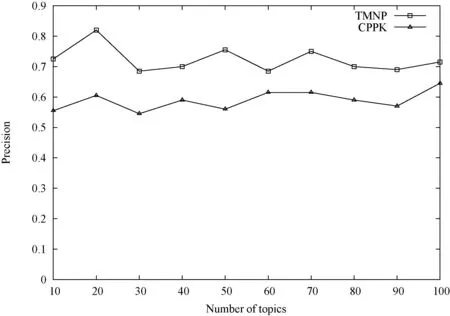
图5 DIP网络TMNP和CPPK算法预测精确度比较
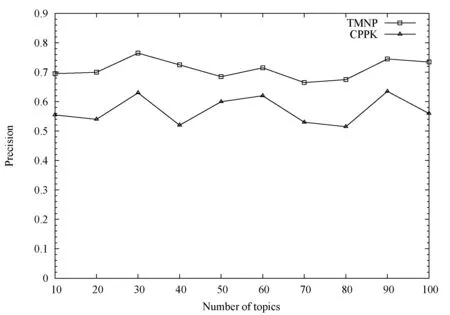
图6 BIOGRID网络TMNP和CPPK算法预测精确度比较
为了验证关键蛋白质序列在主题分布上具有一定的相似性,这里,我们只利用序列主题信息来计算两个蛋白质之间的相似度(即式(5)中ECC的权重系数λ设为0)。我们选取了与初始关键蛋白质集合主题分布最相似的5个潜在关键蛋白质:YGR116W、YNR016C、YHR165、YLR106C、YOR116。并把这5个预测关键蛋白质在BIOGRID蛋白质相互作用网络中可视化出来,如图7所示。在BIOGRID网络中,抽取出包含这5个节点的所有边构成子图。抽取的子图中包含了273个节点和310条相互作用边。可以看出,子图中这5个节点的度数较其他节点高,具有明显的中心性倾向。因此,利用主题信息预测的关键蛋白质在对应物种的PPI网络中体现出了重要的生物调控意义。
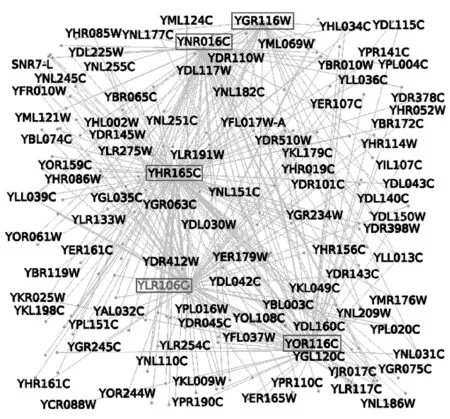
图7 利用主题信息预测关键蛋白质在gcc-BIOGRID网络中的可视化
最后,如图8所示,利用ROC曲线及其对应的AUC值综合测量了基于主题模型和网络拓扑结构的关键蛋白质预测算TMNT算法。并将其和2014年提出的CPPK[21]关键蛋白质预测算法,以及其他两种常用的关键蛋白质预测算法:基于局部平均连接度的方法LAC和网络中心度方法NC进行综合比较。图8中比较了利用随机选取的100个初始关键蛋白质预测100个潜在关键蛋白质在酵母蛋白质数据上的预测结果。其中TMNP的AUC值为0.682,高于CPPK,NC和LAC的AUC值。TMNP的ROC曲线与其他三个识别算法的ROC曲线相比,也更加靠近坐标系左上角。由此可见,TMNP算法的综合性能优于CPPK,NC和LAC关键蛋白质识别算法,达到了比之前更好的识别效果。

图8 算法ROC曲线及AUC值
3 结 语
本文提出在已有的基于蛋白质相互作用网对关键蛋白质预测的算法上加入蛋白质序列信息,用主题模型学习出蛋白质序列的主题向量对原始蛋白质序列进行了基于氨基酸功能信息的特征提取,结合蛋白质相互作用网的拓扑结构对关键蛋白质进行相似度计算,从而预测出潜在关键蛋白质。
该方法利用现有的统计学习理论和数据挖掘方法,从生物体的蛋白质信息中预测发现关键蛋白质从计算角度上解决了通过生物实验寻找关键蛋白质所需要的昂贵代价,并且为研究者们提供了新的生物信息探索途径。
本文序列信息的特征向量距离利用相对熵计算,而在机器学习领域,对特征向量的相似度计算方式有多种。在以后的工作中,可以尝试结合序列向量特征比较其他的向量距离计算方法,从而选择最优的距离计算方式。除此之外,由于每个主题是氨基酸片段的多为分布,可以选取在每个主题下出现概率较大的部分氨基酸片段,分析它们在功能模块调控中的关系,从而“翻译”每个主题的生物意义,即每个主题可能对应的蛋白质功能调控模块。
[1] Winzeler E A, Shoemaker D D, Astromoff A, et al. Functional characterization of the S. cerevisiae genome by gene deletion and parallel analysis[J]. Science, 1999, 285(5429): 901-906.
[2] Kamath R S, Fraser A G, Dong Y, et al. Systematic functional analysis of the Caenorhabditis elegans genome using RNAi[J]. Nature, 2003, 421(6920): 231-237.
[3] Giaever G, Chu A M, Ni L, et al. Functional profiling of the Saccharomyces cerevisiae genome[J]. Nature, 2002, 418(6896): 387-391.
[4] Cullen L M, Arndt G M. Genome-wide screening for gene function using RNAi in mammalian cells[J]. Immunology and Cell Biology, 2005, 83(3): 217-223.
[5] Roemer T, Jiang B, Davison J, et al. Large-scale essential gene identification in candida albicans and applications to antifungal drug discovery[J]. Molecular Microbiology, 2003, 50(1): 167-181.
[6] Wang J, Peng W, Wu F X. Computational approaches to predicting essential proteins: a survey[J]. PROTEOMICS-Clinical Applications, 2013, 7(1-2): 181-192.
[7] Blei D M, Ng A Y, Jordan M I. Latent dirichlet allocation[J]. The Journal of Machine Learning Research, 2003, 3: 993-1022.
[8] Wang H, Ding Y, Tang J, et al. Finding complex biological relationships in recent PubMed articles using Bio-LDA[J]. PLoS One, 2011, 6(3): e17243.
[9] Zhang J, Liu B, He J, et al. Inferring functional miRNA-mRNA regulatory modules in epithelial-mesenchymal transition with a probabilistic topic model[J]. Computers in Biology and Medicine, 2012, 42(4): 428-437.
[10] Pan X Y, Zhang Y N, Shen H B. Large-Scale Prediction of Human Protein—Protein Interactions from Amino Acid Sequence Based on Latent Topic Features[J]. Journal of Proteome Research, 2010, 9(10): 4992-5001.
[11] Tatsuya Asou, Koji Eguchi. Predicting protein-protein relationships from literature using latent topics[J]. Genome Inform, 2009,23(1):3-12.
[12] Griffiths T L, Steyvers M. Finding scientific topics[J]. Proceedings of the National Academy of Sciences, 2004, 101(1): 5228-5235.
[13] Jeong H, Mason S P, Barabási A L, et al. Lethality and centrality in protein networks[J]. Nature, 2001, 411(6833): 41-42.
[14] Wang J, Li M, Wang H, et al. Identification of essential proteins based on edge clustering coefficient[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2012, 9(4): 1070-1080.
[15] Hao D, Ren C, Li C. Revisiting the variation of clustering coefficient of biological networks suggests new modular structure[J]. BMC Systems Biology, 2012, 6(1): 34.
[16] Li M, Zhang H, Wang J, et al. A new essential protein discovery method based on the integration of protein-protein interaction and gene expression data[J]. BMC Systems Biology, 2012, 6(1): 15.
[17] Hart G T, Lee I, Marcotte E M. A high-accuracy consensus map of yeast protein complexes reveals modular nature of gene essentiality[J]. BMC Bioinformatics, 2007, 8(1): 236.
[18] Engel S R, Dietrich F S, Fisk D G, et al. The reference genome sequence of saccharomyces cerevisiae: then and now[J]. G3: Genes, Genomes, Genetics, 2014, 4(3): 389-398.
[19] Xenarios I, Rice D W, Salwinski L, et al. DIP: the database of interacting proteins[J]. Nucleic Acids Research, 2000, 28(1): 289-291.
[20] Stark C, Breitkreutz B J, Chatr-Aryamontri A, et al. The BioGRID interaction database: 2011 update[J]. Nucleic Acids Research, 2011, 39(1): 698-704.
[21] Li M, Zheng R, Zhang H, et al. Effective identification of essential proteins based on priori knowledge, network topology and gene expressions[J]. Methods, 2014, 67(3): 325-333.
[22] Li M, Wang J, Chen X, et al. A local average connectivity-based method for identifying essential proteins from the network level[J]. Computational Biology and Chemistry, 2011, 35(3): 143-150.
[23] Deshwar A G, Morris Q. PLIDA: cross-platform gene expression normalization using perturbed topic models[J]. Bioinformatics, 2014, 30(7):956-961.
[24] Mewes H W, Frishman D, Mayer K F X, et al. MIPS: analysis and annotation of proteins from whole genomes in 2005[J]. Nucleic Acids Research, 2006, 34(1):169-172.
[25] Cherry J M, Adler C, Ball C, et al. SGD: Saccharomyces genome database[J]. Nucleic Acids Research, 1998, 26(1):73-79.
[26] Zhang R, Lin Y. DEG 5.0: a database of essential genes in both prokaryotes and eukaryotes[J]. Nucleic Acids Research, 2009, 37(1):455-458.
[27] Saccharomyces Genome Deletion Project[OL]. http://www-sequence.stanford. edu/group/.
IDENTIFYING ESSENTIAL PROTEINS BY INTEGRATING TOPIC FEATURES AND INTERACTION NETWORKS TOPOLOGICAL FEATURES
Cui XinShao Mingyu
(SchoolofComputerScience,FudanUniversity,Shanghai200433,China)
Essential proteins are those proteins that are indispensable to the viability and reproduction of an organism. Identification and prediction of essential proteins has great significance for us to understand the minimal protein sets required for organism life, besides it also plays important role in the fields of drug design and drug target discovery. Most existing essential proteins identification algorithms are based on the topological features of protein-protein interaction networks. This work introduces a new feature into the identification algorithm proposed, which considers the topic distribution feature of essential proteins’ sequences themselves. By introducing LDA model into CPPK algorithm, which is based on topological features of protein-protein interaction networks, we proposed a new essential protein identification method: the essential proteins identification integrating topic model and protein-protein interaction networks topological features. This new algorithm was tested on Saccharomyces protein dataset, and was compared with some state-of-art essential proteins identification algorithms. Experimental result showed that by introducing LDA model and new features to improve original CPPK prediction algorithm, better identification performance than previous algorithm was achieved.
Topic modelCentrality measureProtein-protein interaction networkEssential protein
2015-04-20。崔鑫,硕士生,主研领域:数据挖掘,生物信息学。邵明玉,博士生。
TP3
A
10.3969/j.issn.1000-386x.2016.08.063
