改进的增量贝叶斯模型的研究

苏志同　李　杨

(北方工业大学计算机学院　北京 100144)



改进的增量贝叶斯模型的研究

苏志同李杨

(北方工业大学计算机学院北京 100144)

传统分类算法的研究主要关注批量学习任务。实际中，带标注样本很难一次性获得。且存储空间开销较大的特点，也使批量学习显现出一定的局限性。因此，需要增量学习来解决该问题。朴素贝叶斯分类器简单、高效、鲁棒性强，且贝叶斯估计理论为其应用于增量任务提供了基础。但现有的增量贝叶斯模型没有对适应新类别作出描述。同时，实验表明类别之间样本数量的不平衡，会严重影响该模型的分类性能。故基于这两个问题，提出对增量贝叶斯模型的改进，增加参数修正公式，使其可适应新出现的类别，并引入最小风险决策思想减轻数据不平衡造成的影响。取UCI数据集进行仿真测试，结果表明改进后的模型可以渐进提高分类性能，并具有适应新类别的能力。

机器学习朴素贝叶斯增量学习最小化风险

0　引　言

分类问题的研究是监督学习研究的核心任务之一。可以将分类描述为根据已知数据集，建立分类器(决策函数或概率模型)，再利用分类器判断未知样本类别的过程。建立分类器过程，称为学习。而利用分类器判断的过程，称为预测。依据样本获得过程与模型学习过程的具体特点，学习任务可分为批量学习任务与增量学习任务[1]。Giraud-Carrier指出，增量学习任务具有样本随时间获得，并且学习过程需持续进行的特点。而传统机器学习算法的研究假设训练集可以一次性获得，一旦训练集被充分处理后，学习就结束了。所获得的模型仅仅用于对新实例的预测。虽然对批量学习算法稍做修改，所得暂时批量学习算法[2]可应用于增量任务，但是要存储已学习过的样本，用重新训练的方式更新模型，这增加了额外的时空开销。与此方法相比，Polikar[3]面向监督学习任务，定义增量学习算法应当满足从新数据中学习新的知识，不需要访问当前分类器学习过的数据，仅保存当前所获得的知识，可以适应具有新的类别标记的样本。基于这种思想，Polikar等人提出了一种针对有监督任务的增量学习算法Learn++，增量地训练多层感知机(MLP)，并将之运用于分类任务中。对UCI的部分数据集及一些现实数据进行仿真测试，证明算法使得多层感知机的分类性能随着训练数据的增加得以提高，且成功适应了新引入的类别。此后，在传统算法基础上，前人提出了很多增量算法。从所获得的模型角度来看，一些算法以较少的时空代价，对多个训练子集进行增量学习，从而获得与在全部训练集进行批量训练近似的模型，进而达到近似的分类效果。如支持向量机(SVM) 的增量版本[4-6]及增量决策树ID4[7]。另一类算法则是，可以获得与批量学习相同的模型，如增量决策树ID5R[8]。从Polikar等所定义的增量学习所满足的条件来看，除针对新样本数据进行增量学习外，还可以学习新的样本类别，如Jia H等人提出的SVM的类别增量学习算法[10]。

因此，可以认为增量任务分为对数据或样本的增量学习和对新引入类别的增量学习。朴素贝叶斯模型以其很好的鲁棒性与分类精度[11]成为处理分类任务重要模型。而贝叶斯参数估计理论为其能够在连续学习的过程中，利用样本信息修正当前模型提供了的理论依据。宫秀军等人对基于贝叶斯理论的增量学习进行了详细论证，并给出了完整的增量贝叶斯分类模型[9]。随后，在诸多场景下都得以应用，如病毒上报分析的应用[12]与中文问句分类[13]等。虽然增量贝叶斯分类模型的提出很好地解决了在类别平衡的数据集上，对样本的增量学习。但是该模型存在两点不足。其一，该模型并没有对新出现的类别增量予以描述。其二，并非从所有领域中收集而来的训练集都是类别平衡的。在不平衡数据集中，往往一些类别被大量的样本过度的表达。相反代表另一些类别的样本数量却很少。从而导致分类器不能识别少数样本所代表的类别。故本文在其基础之上，基于贝叶斯估计方法对增量贝叶斯模型进行扩展，实现对新类别适应。并提出一种代价函数使之结合最小化风险决策，从而克服从不平衡数据集学习分类器的问题。

1　增量贝叶斯模型

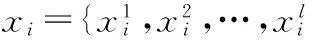
表1　类别分布律

此分布中存在m-1个参数，记为ξ=(ξ1,ξ2,…,ξm-1)。将训练集中的样本视为n次独立实验的观测结果，则其似然函数可表示为式(1):

(1)

其中：ui为样本集中类别yj出现的次数，且∑ui=n。

贝叶斯参数估计方法需要将所估计的参数看作随机变量，假设已经掌握了关于ξ的先验k0，所以假设在事先得知ξ的先验分布为p(ξ|k0)。通过获得的样本x1,x2,…,xn计算后验分布p(ξ|k0,x1,x2,…,xn)，最终用后验分布下ξ的期望值作为估计结果。当只有一个已知样本x1时，计算后验分布如下:

(2)

当获得两个样本x1,x2时，计算后验分布如下：

(3)

此时，ξ的先验分布变为p(ξ|K0,x1)，即先验知识由k0变为了(K0,x1)。以此类推可得Ki+1=Ki+xi。当样本是连续获得时，可将当前计算的后验结果作为新样本获得后再次进行估计的先验来使用，即增量地修正估计结果。

特别地，后验分布与先验分布共轭时效果最佳。根据此问题的似然结构应取dirichlet分布作为参数ξ的先验分布。式(4)给出了其概率密度与数学期望，其中(α1,α2,…,αm)称作超参数且α=∑αi。

=dirichlet(α1,α2,…,αm)

(4)

p(ξ|K0,x1,x2,…,xn)

=dirichlet(α1+u1,α2+u2,…,αm+um)

0≤ξ1+ξ2+…+ξm-1<1

(5)

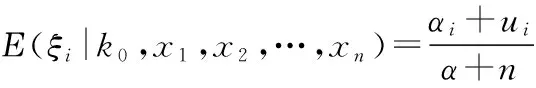
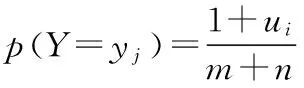
(6)

(7)

增量贝叶斯模型的提出，从参数估计的角度，给出了增量修正模型参数方法。更重要的是，贝叶斯估计理论使得分类器仅仅通过累加操作就能应用于增量学习任务中，实现了随样本的获得而动态修正模型参数，并最终获得与朴素贝叶斯在完整数据集进行批量学习相同的模型，从而克服了批量学习要求样本一次性获得的问题。

2　类别的增量学习

前人提出的增量贝叶斯模型属于数据增量的范畴，用于不能一次性获得全部训练数据的场景。通过不断学习新产生的样本修正当前模型，从而改善预测性能。所以在式(7)中看到，对新引入类别，该如何处理，并没有给出描述。对于新出现类别进行增量学习，使得分类模型随着这种样本的不断出现而逐渐学习这个类别的知识，最终实现对此类别的识别，在一些实际问题中是重要的。因为在学习过程中数据是随时间产生的，很难保证每次产生的增量集都包含所有类别的样本。在复杂系统中，重新训练模型的代价有时是难以接受的。如文献[16]所描述的生物图像数据库的建立，全部物种图像不能一次性获得的，起初的分类器并不能正确识别新的物种图像。因此，系统应当增量的学习新类别图像的知识，而非对系统进行重新训练。故本文基于贝叶斯估计方法，对于学习带有新类别标示的样本时，参数估计与模型修正公式进行论证。并给出了修正方法的数学表达。

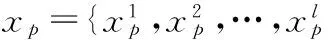
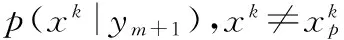
(8)

与此同时，应当对模型中的其他p(Y=yi),i≠m+1参数进行修正，如式(9)：

(9)

(10)

(11)

至此，给出完整类别增量修正参数的数学表达如式(12)，对带有新类别的样本，学习的过程就是向原有模型添加新参数，并对其进行估计，再将其他相关参数进行修正的过程。

(12)

3　样本选择与类别间的不平衡性

文献[9]中认为增量学习过程中，对于增量集中的标记数据应当逐渐全部学习，随后用半监督学习方式追加一定数量的无标记数据进行训练，以提高分类效果。并使用精度作为衡量分类效果的标准。这种方式存在三个问题，其一，实验表明并非所有标记样本都是值得学习的，应采取相应的策略对待学习样本进行甄选。其二，其假设所使用的训练集中各类别被近似相同数量的样本所代表，而在一些情况中，数据集中的类别分布是非常不平衡的[17]。最后，在数据不平衡的情况下仅仅用精度来衡量分类性能是片面的。因此，本文引入最小化风险决策的思想克服此问题，并分别从精度与召回率两个角度进行分析评价。

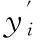
(13)

(14)

取UCI数据集中Car Evaluation对增量贝叶斯模型进行验证，数据集由4种类别的1728个实例构成，每个实例有6个特征属性与1个类别属性。从完整数据集中，取其中3种类别的1663个实例用来测试。随机取出663个实例作为测试集，记为T。剩余数据共有1000个实例涵盖3种类别，将其记为D。再将D分为5份，记为S1…S5。每个子集随机分配200个实例 ，使用增量学习方式进行训练。同时，使用朴素贝叶斯在D上做批量训练。在测试集T上对比二者精度，实验结果如表2所示。

表2　精度测试结果

从结果中看出，模型精度并没有随着学习样本数量的增多而提高的。相反地，模型精度呈现下降趋势，直至获得与朴素贝叶斯在全集D上批量学习相同的模型为止。单纯通过学习更多的带标注样本的训练方式，在一些情况下，会对提高模型精度起反作用。如果待学习的样本不能改善分类器性能，那么对这些样本的学习就会既费时又无用。

同时，由于训练集中样本数量具有典型的不平衡性特点，造成少数样本代表的类别呈现不可接受的低识别率。表3列出了Car Evaluation实验集的类别数量比例与上述增量方法在完成全部增量学后对每个类别的召回情况。从中很直观地反映出样本数量倾斜所导致的good类别完全不识别，极大地削弱了分类器的决策价值。

表3　测试结果

对于有标注样本的学习，文献[15]中认为被当前分类器错分的样本往往带有更多有价值的信息，应对优先选择错分样本进行学习。而对于训练集的不平衡性问题，从决策风险的角度来看，传统贝叶斯分类器基于最大化后验概率进行决策，其本质等价于在0-1损失下最小化风险。这种决策假设所有的错误决策的风险都是相同的。考虑到数据集样本数量的不平衡性，0-1损失显然是不合理的。故本文提出错分代价函数如式(15)。其中count(yi)表示当前训练集中类别为yi的样本个数，0<α<1作为一种对决策错误的惩罚参数。当α<0.5时，可体现出将训练集中数量少的类别被预测为数量多的类别，其代价更高。从而使得决策对数量少的类别更加关注。

(15)

进而依据贝叶斯决策理论，此时的风险计算变为了如式(16)所示。而决策也有最大化后验概率变为了最小化风险。故决策函数也相应调整为式(17)所示:

R(yi|x)=∑p(yj|x)·cost(yj,yi)

(16)

(17)

至此，本文提出一种改进的增量学习算法。在进行增量学习之前，首先，根据当前各类别样本的数量分布，计算代价矩阵，使用当前模型对增量集进行分类，获得所有被错分的样本形成集合。为了在训练阶段尽量平衡各类别的样本数量，采取优先学习少数样本代表的类信息，故将错分集合中样本按其类别在训练集中存在的数量进行升序排序。取出升序后的第一个样本进行学习，更新贝叶斯模型。随后，更新代价矩阵。再将已学样本从增量集中删除。重复此过程，直至增量集为空或没有新的错误样本产生。算法描述如下:

增量学习算法模型建立过程:输入:初始训练集D,错分代价参数α输出:初始贝叶斯模型与代价矩阵利用D建立贝叶斯模型M,并获得每个类别样本的数量存于向量ynum[]中;

通过式(15)和ynum计算代价矩阵C;增量学习过程:输入:增量集S,错分代价参数α输出:更新后的分类模型定义错分集合wset;do初始化错分集合wset为空;fori=1:|S|用当前模型M对(xp,yp)进行预测;将错分样本xp保存于错误集wset中;Endfor;将wset中的样本按它们类别在训练集中存在的数量进行升序排序;if|wset|>0 从wset中取出第一个错分样本(xp,yp); ifyp∉Y通过式(12)更新M,并更新ynum;再利用ynum更新代价矩阵C; 从S中删除xp; Else通过式(7)更新M,并更新ynum;再利用ynum更新代价矩阵C; 从S中删除xp;Elsebreak;Endif;While(|S|>0);

4　代价函数中参数取值分析

由于本文提出的决策风险函数中含有一个惩罚参数，故现取UCI中的两个不平衡程度不同的数据集验证本文算法，从而给出数据集不平衡程度与参数取值关系的分析。所选用的数据集信息如表4列出。从中可见，car数据集属于严重不平，而Spect heart的不平衡程度较轻。

表4　数据集信息

为使得决策更倾向于少数两样本的类别，参数的取值应为α∈[0,0.5]，在此区间上进行取值。按照上文的做法，将两个数据集，都分为6份，5份用于训练，1份用于测试。分析不同参数取值对各类别召回率的影响，揭示二者之间的关系。图1与图2给出了两个数据集各类别召回率随参数取值的变化趋势。

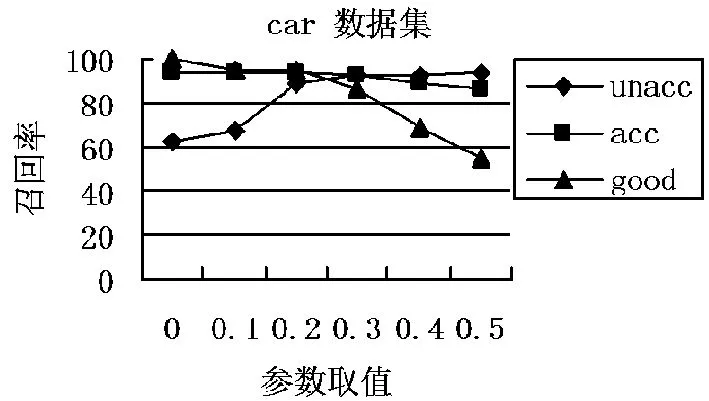
图1参数与类别召回率的关系

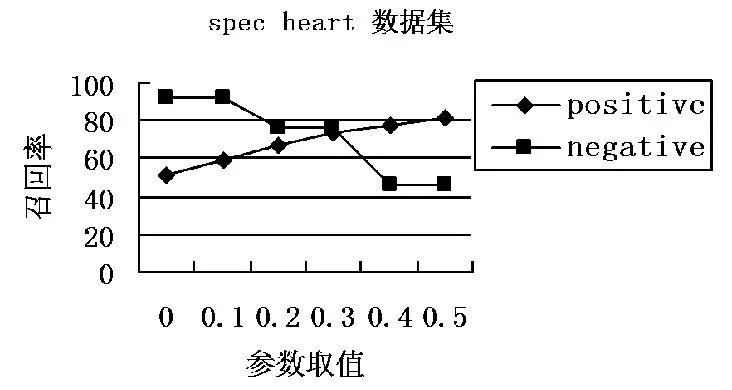
图2参数与类别召回率的关系

现从两个角度对上述趋势进行分析。由于数据集的不平衡，决策应更加关注少数类别。所以，原则上参数取值应越小越好。如图1与图2所示，参数取值越接近0，对少数类别的召回率越接近1。但同时，一旦参数取值超过一定界限，便会对原本的多数类别的识别造成影响。图中同样反应出，当少数类别的召回接近1时，多数类别的识别呈下降趋势。原因是当决策对少数类别的倾向到一定极端程度时，少数类别的样本达到了完全识别，而错分集中不再包含少数的类别。在依照算法，依然错分样本进行学习，不断增加多数类别样本的学习数量。更加加剧了决策向少数类别的倾斜。所以，最理想的参数取值应为两图中，各类别召回曲线的交点处。其次，图示所反映的另一种关系则是训练集的不平衡程度与参数的取值。理想的参数取值应可以反映训练的不平衡的程度。正如car集的程度相对于Spect heart集更严重，故其参数取值也应比Spect heart集的参数取值更小。

5　实验结果及分析

为验证模型与算法的有效性，取UCI机器学习数据集中的部分数据分别进行数据增量与类别增量的验证。并将朴素贝叶斯(NB)与本文算法进行对比。表5列出了数据集信息。

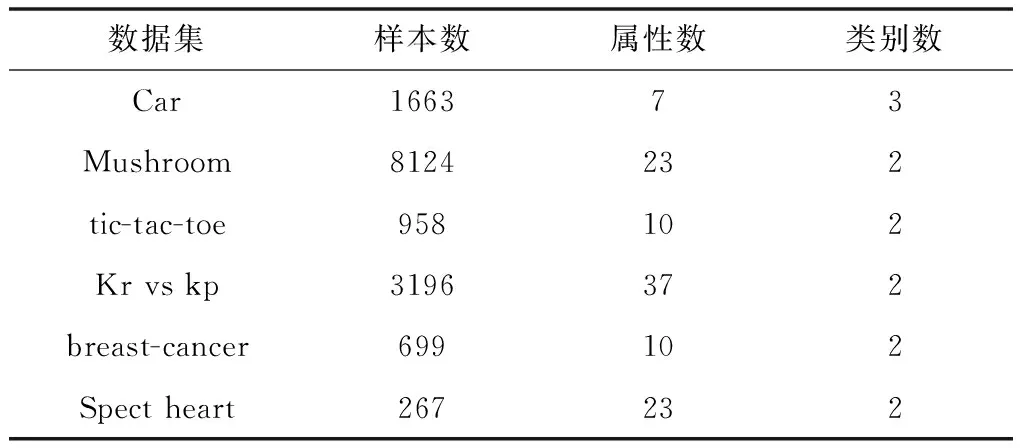
表5　数据集信息

进一步对上述数据进行简单处理，先将上述每个实验数据集都随机分为两个部分，即训练集与测试集。再将每个训练集平均分为5份为增量学习做好准备，各个子集的实例随机分配。表6描述了每个实验集的划分情况。

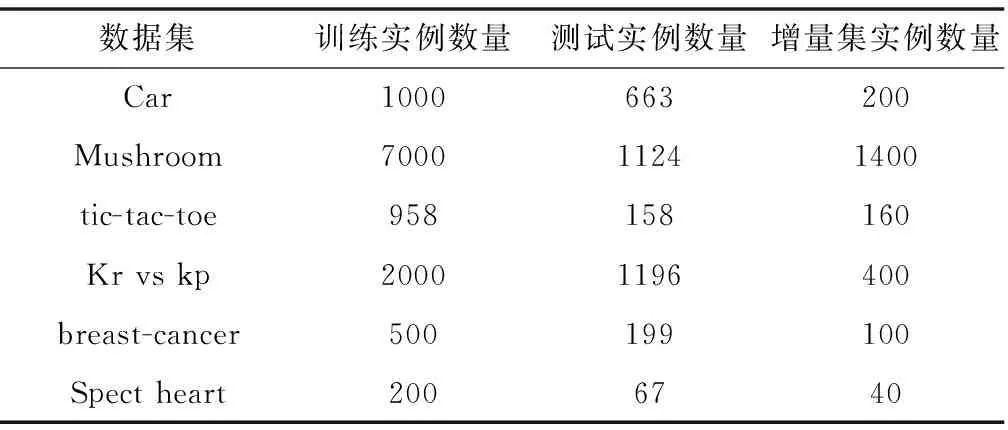
表6　实验准备

首先，验证在6个数据集上验证数据增量学习。为了得到更为客观的实验结果，按照上述数据集划分比例，在每个实验数据集上，做5次增量学习直至将完整训练全部学习。同时，每个实验集，做5折交叉验证，交替对换训练集与测试集中的数据，取5次验证的结果的均值作为结果的估计，再与朴素贝叶斯在每个完整训练集上的5折交叉验证结果的均值做比对。表7则给出了精度结果的对比。

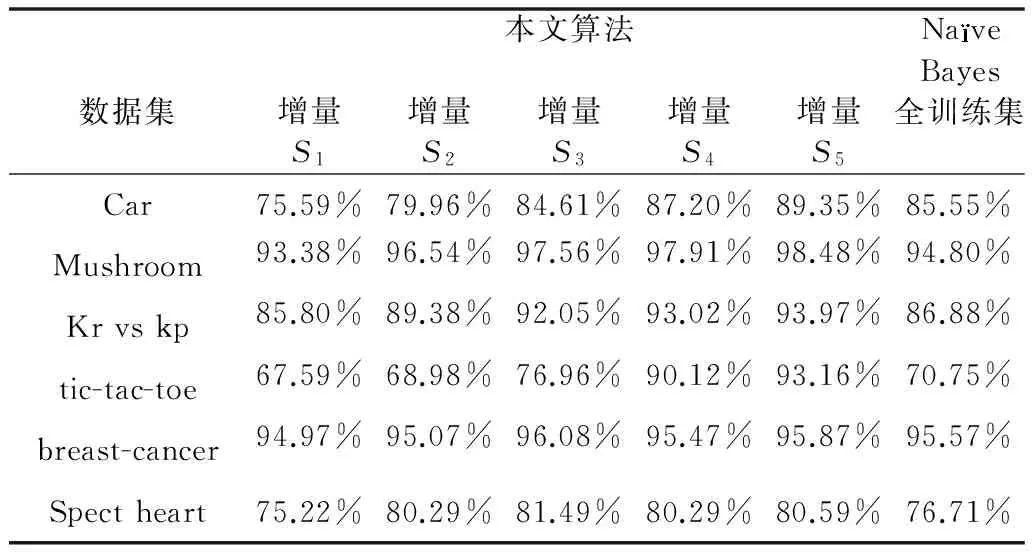
表7　精度对比

表8则列出了本文方法与朴素贝叶斯，在4个不平衡数据集上，各类别召回情况的对比。

表8　召回对比

从上述实验结果不难发现，在增量学习过程中，选择适当的样本进行学习可以逐渐提高分类器精度。同时，由于风险决策的引入使得决策更加的均衡，从而克服了不平衡训练的带来的影响。

再次取涵盖4个类别的完整car数据集，进行类别增量学习的验证。仍然将此数据集划分为两个部分，即训练集与测试集。其中，训练集实例个数为1000，而测试集实例个数为728，涵盖全部4给类别。同样将训练集划分为5个增量子集，将其记为S1,…,S5，而测试集记为T。S1至S2仅仅包含unacc与acc两个类别的实例。S3至S4包含unacc、acc与good三个类别的实例。S5则包含全部4个类别的训练实例。表9给出了5次增量训练，在每一次学习后，测试精度的变化。

表9　类别适应

表9中的结果反映出在增量集S1至S2阶段，分类器维持在较低精度。由于此时的训练集并不包含good与vgood这两种类别。所以，分类器不能识别测试集中的两种类别，再加之对一部分已知类别的误判，使得错误率较高。 随后，在增量集S3与S5被引入后，分类器的性能均有一次较明显的改善，则是由于引入了代表新类别的训练实例，使得分类器可以逐渐识别类别good与vgood。最终实现了测试集中全部4个类别的适应。

6　结　语

本文基于贝叶斯估计理对增量贝叶斯模型进行扩展，使其可适应新出现的类别，并引入最小化风险决策克服了不平衡数据集上少数类别召回率低的问题。利用UCI数据集进行测试，证明了改进后的增量模型可以渐进提高分类性能，并具有适应新类别的能力。但本文给出的代价函数仍存在一定的局限性。特别是参数的确定问题，将是我们后续研究的重点。

[1] Giraud Carrier C.A note on the utility of incremental learning [J].AI Communications,2000,13(4): 215-223.

[2] Maloof M A,Michalski R S.Selecting examples for partial memory learning [J].Machine Learning,2000,41(1): 27-52.

[3] Polikar R,Upda L,Upda S S,et al.Learn++: An incremental learning algorithm for supervised neural networks[J].Systems,Man,and Cybernetics,Part C: Applications and Reviews,IEEE Transactions on,2001,31(4): 497-508.

[4] Xiao R,Wang J,Zhang F.An approach to incremental SVM learning algorithm[C]//Tools with Artificial Intelligence,2000.ICTAI 2000.Proceedings.12th IEEE International Conference on.IEEE,2000: 268-273.

[5] Wenhua Z,Jian M.A novel incremental SVM learning algorithm[C]//Computer Supported Cooperative Work in Design,2004.The 8th International Conference on.IEEE,2004,1: 658-662.

[6] Wang W J.A redundant incremental learning algorithm for SVM[C]//Machine Learning and Cybernetics,2008 International Conference on.IEEE,2008,2: 734-738.

[7] Schlimmer J C,Fisher D.A case study of incremental concept induction[C]//AAAI.1986: 496-501.

[8] Utgoff P E.Incremental induction of decision trees[J].Machine learning,1989,4(2): 161-186.

[9] Gong X J,Liu S H,Shi Z Z.An incremental Bayes classification model[J].Chinese Journal of Computers,2002,25(6): 645-650.

[10] Jia H,Murphey Y L,Gutchess D,et al.Identifying knowledge domain and incremental new class learning in SVM[C]//Neural Networks,2005.IJCNN’05.2005 IEEE International Joint Conference on.IEEE,2005,5: 2742-2747.

[11] Domingos P,Pazzani M.On the optimality of the simple Bayesian classifier under zero-one loss[J].Machine learning,1997,29(2-3): 103-130.

[12] Chen L,Zhen N,Guo Y H,et al.Applying Naive Bayesian Incremental Learning In Virus Reporting and analyzing[J].Computer Applications and Software,2010,27(1): 92-95.

[13] Di S,Li H,He P.Incremental Bayesian classification for Chinese question sentences based on fuzzy feedback[C]//Future Computer and Communication (ICFCC),2010 2nd International Conference on.IEEE,2010,1: V1-401-V1-404.

[14] Jeffreys S H.Theory of Probability[M].3d Ed.Clarendon Press,1967.

[16] Ditzler G,Rosen G,Polikar R.Incremental learning of new classes from unbalanced data[C]//Neural Networks (IJCNN),The 2013 International Joint Conference on.IEEE,2013: 1-8.

[17] García-Pedrajas N,Pérez-Rodríguez J,de Haro-García A.OligoIS: scalable instance selection for class-imbalanced data sets[J].Cybernetics,IEEE Transactions on,2013,43(1): 332-346.

ON IMPROVED INCREMENTAL BAYESIAN CLASSIFICATION MODEL

Su ZhitongLi Yang

(CollegeofComputer,NorthChinaUniversityofTechnology,Beijing100144,China)

The research of traditional classification algorithm focuses on the batch learning tasks.Actually,it is not easy to obtain labelled samples once for all.In addition,there is certain limitation in batch learning tasks because the cost of storage space is rather high.Therefore,incremental learning can be referred to as a solution.Naive Bayesian classification is simple,efficient and highly robust,besides,the theory of Bayesian estimation lays the foundation for its application in incremental tasks.However no existing incremental Bayesian model has described the adaptation to new classes.Moreover,the experiment shows that the imbalance in numbers of different samples between classes will have a great impact on the classification performance of the model.Therefore,based on the above two problems,we present to improve the incremental Bayesian model and to increase of formulas of parameters modification so as to enable the model to adapt to new classes.Also the idea of risk decision minimisation is introduced to reduce the impact of data imbalance.Simulation is carried out on UCI dataset,result indicates that the improved incremental model can improve the classification performance gradually and has the adaptability to new classes.

Machine learningNaive BayesIncremental learningRisk minimisation

2015-03-16。国家自然科学基金项目(61105045);中央支持地方专项(PXM2014_014212_000097);北方工业大学科研人才提升计划项目(CCXZ201303)。苏志同，教授，主研领域：数据挖掘、数字媒体技术。李杨，硕士生。

TP181

A

10.3969/j.issn.1000-386x.2016.08.057