基于Abaqus的三偏心水电主控蝶阀密封性研究

何庆中，王渝皓，王　佳，厉明玉

(四川理工学院机械工程学院，四川自贡643000)



基于Abaqus的三偏心水电主控蝶阀密封性研究

何庆中，王渝皓，王佳，厉明玉

(四川理工学院机械工程学院，四川自贡643000)

针对某水电站大型三偏心蝶阀(DN3400)在实际运行过程中出现的问题，利用Abaqus软件对其密封性能进行了分析研究。通过分析结果与传统经验计算以及实际问题的对比分析，证明了分析方法的合理性。改变三偏心蝶阀的三个偏心值，通过大量的仿真实验得到了相应的模拟结果，找到了不同偏心值与密封性能的关系，为提高大型三偏心蝶阀的密封性能提供了理论依据。

蝶阀；Abaqus软件；偏心值；密封性能

0　引　言

蝶阀具有切断、调节和止回3种功能，三偏心蝶阀作为蝶阀中最高级的一种，其密封性能最佳，广泛应用于石油、化工、电力等行业。它的可靠性、节能性、制造和运行成本对于国民经济具有重要的意义。目前在我国的中西部地区，中大型水电站的主控阀一般使用大口径蝶阀或大型球阀。然而由于蝶阀在加工制造、调控以及密封性等方面相对球阀都有一定的优势，因此对大型蝶阀的研究具有重要的意义。本课题针对某水电站口径为3 400 mm 的大型水电主控三偏心蝶阀在实际运用中出现的顶部密封性差，对其密封性进行了研究，得到了大口径水电主控蝶阀密封性能合理的分析方法，同时找到了大口径三偏心蝶阀的3个偏心值与密封性能的规律分布，为以后大型蝶阀的设计提供理论依据。

1　三偏心原理及密封比压理论计算

1.1三偏心原理

根据偏心原理蝶阀分为中心对置蝶阀、单偏心蝶阀、双偏心蝶阀和三偏心蝶阀，单偏心蝶阀只有轴向偏心，双偏心蝶阀有轴向和径向偏心。三偏心蝶阀在双偏心蝶阀基础上进行改进，增加了圆锥密封面中心线偏角，从而减小了阀门启闭过程中密封副的摩擦力，极大的降低了密封副的磨损，同时密封副的密封方式得到了改进，由原来的线密封提高到圆锥面密封，这样使蝶阀密封面的密封比压更加均匀，大大提高了蝶阀的密封性能。三偏心蝶阀结构如图1所示。

图1　蝶阀结构

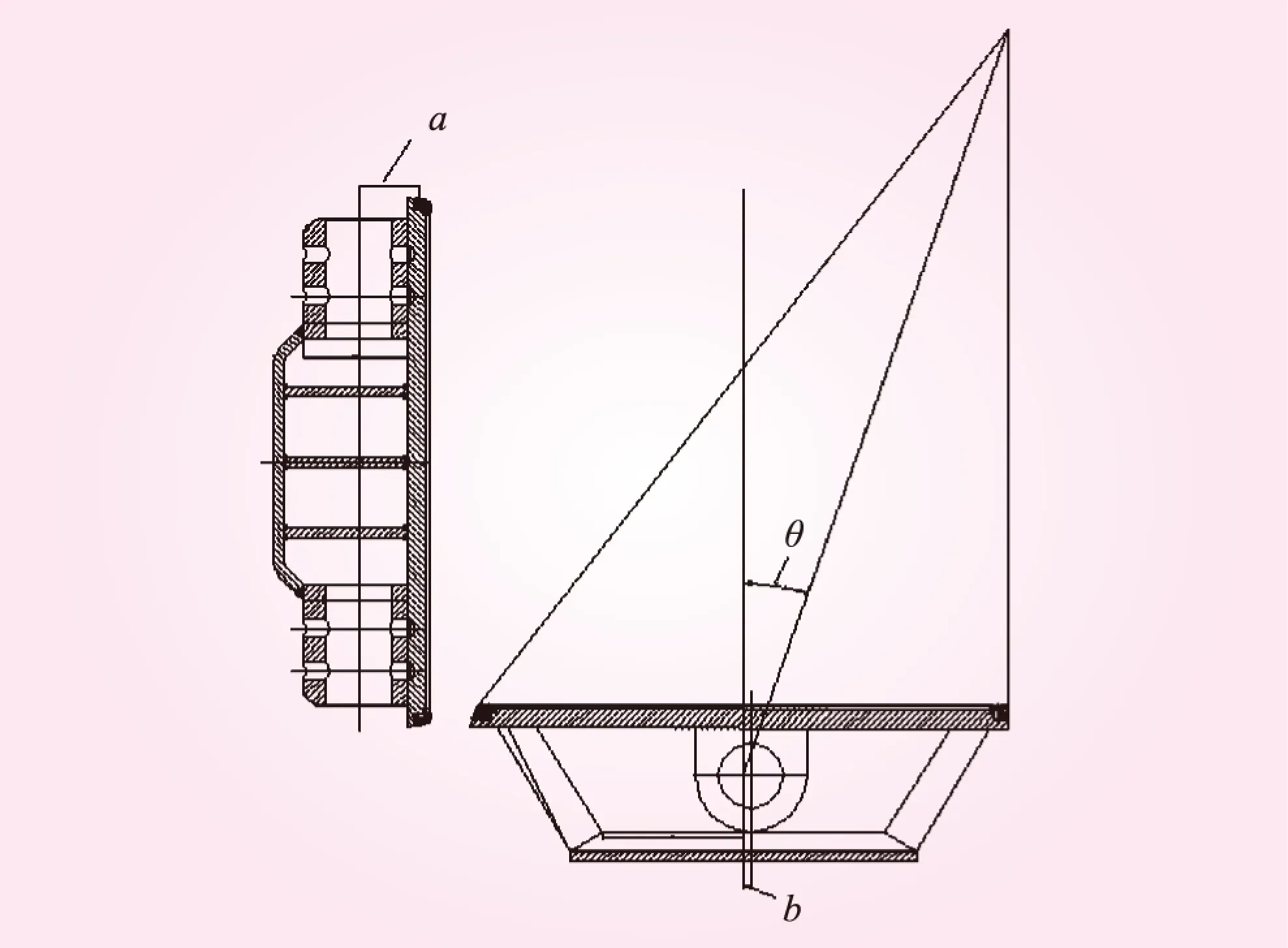
图2　三偏心结构原理

三偏心蝶阀的结构原理如图2所示，其中第一个偏心值a为轴向偏心，第二个偏心值b为径向偏心，第三个偏心值θ为锥面中心线偏角。轴向偏心a保证了密封面为一个连续的圆锥面，同时由于该偏心的存在，方便了密封面加工时几何中心的确定，降低的制造难度。由于径向偏心和角偏心的存在，使得蝶板密封面的回转半径小于阀座密封面的回转半径，避免了阀门启闭过程中产生干涉。

三偏心蝶阀圆锥密封面为一个复杂的曲面，它的加工精度与加工方法直接决定了阀门的密封性能。该曲面任意一个横截面轮廓线均为椭圆，平面斜截圆锥如图3所示。

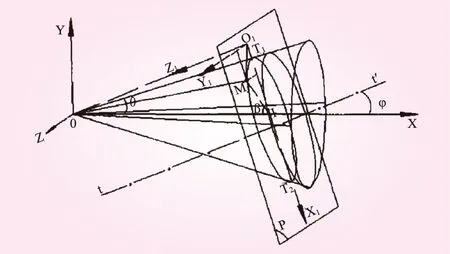
图3　平面斜截圆锥

椭圆方程为

(1)

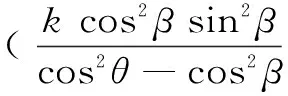
1.2密封比压理论计算

金属硬密封的密封面法向方向的压强为密封比压，其大小为

(2)

式中，F为法向方向受力；S为密封面积。查阅相关资料，三偏心蝶阀密封比压的理论经验计算公式为

(3)

式中，ΔP为密封两侧的压差；B为密封面的宽度。蝶阀关闭时正面的静水压为4 MPa，由于密封面为不规则曲面，取其平均宽度B=0.06 m，代入式(3)得到密封比压q=118.41 MPa。

2　接触分析理论基础

2.1非线性分析

有限元非线性分析包括材料非线性、几何非线性和边界条件非线性。材料非线性是指材料的应力应变关系为非线性，如弹塑性分析。几何非线性及位移的大小对结构的响应发生影响，包括大位移、大转动、初始应力、几何刚性化和突然翻转等问题。

边界条件非线性是指边界条件在分析过程中发生变化。接触问题就是一种典型的边界条件非线性问题，其特点是：边界条件不是在计算的开始就可以全部给出，而是在计算过程中确定，接触体之间接触面积和压力分布随外载荷变化，同时还可能需要考虑接触面间的摩擦行为和接触传热。

2.2接触类型

两接触面的接触状态可以分为三类。

第一类为两接触体处于分离状态，此时接触释放。

(4)

第二类为粘式，即两面处于接触状态但无相对滑动。

(5)

第三类为滑移，即两面接触且接触面有相对滑动。

(6)

式中，A、B表示两个接触面；Pξ、Pε分别表示两接触面的法向作用力和切向摩擦力；Uξ、Uε分别表示接触面的法向位移和切向位移；0Dξ表示两接触面的初始间隙；μs表示静摩擦因数；0()、Δ()分别表示初始值和增量值。

本分析的接触状态为第三类，采用的接触公式为小滑移，ABAQUS/Standard在分析的开始就从面节点和主面的哪一部分发生接触，在整个分析过程中这种接触关系不会发生变化。

3　有限元分析计算

3.1三偏心蝶阀数学模型的建立

通过三维建模软件soliworks建立了蝶阀的三维数学模型，如图4所示。

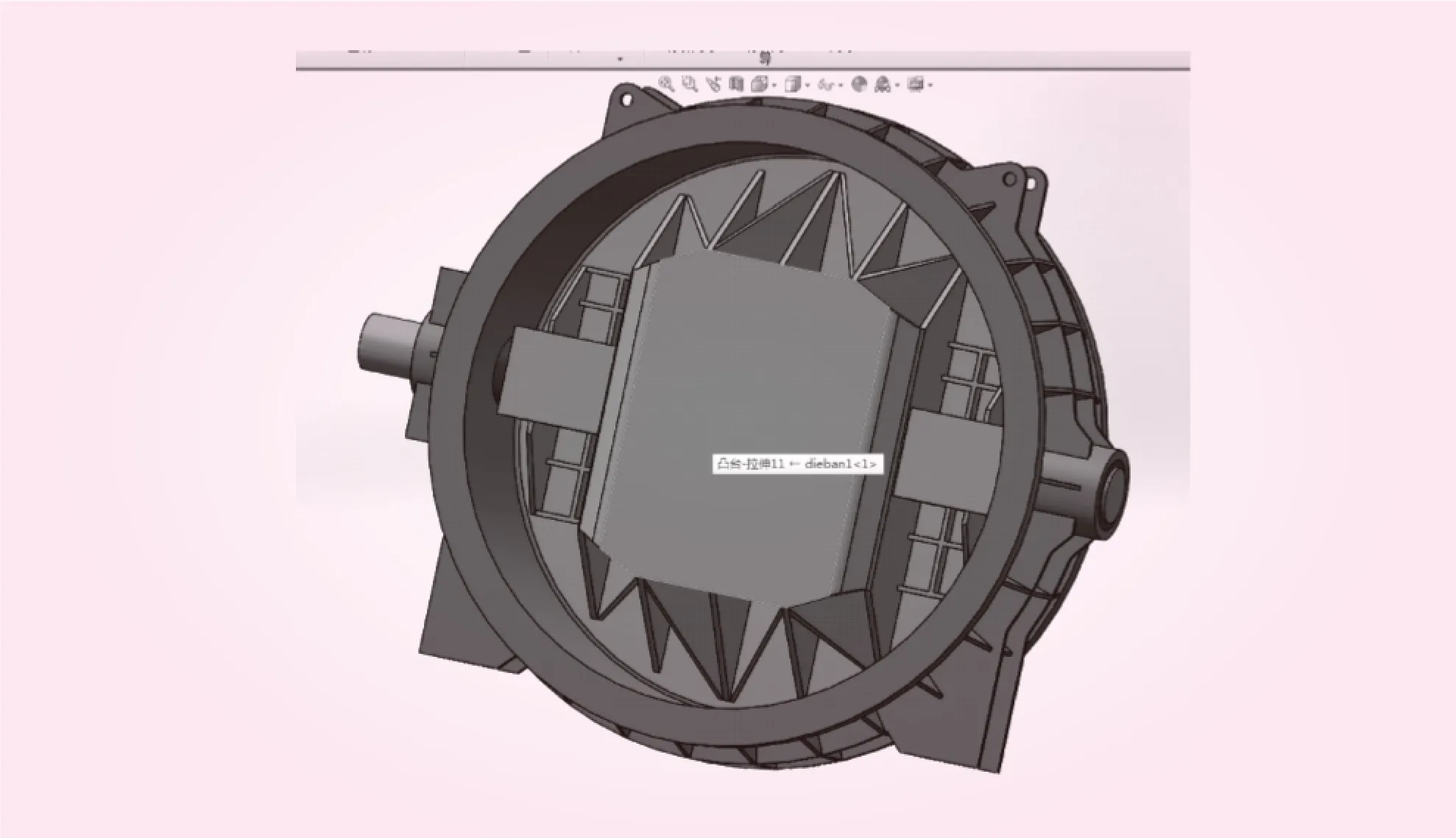
图4　蝶阀三维数学模型

3.2有限元模型的建立

将三维模型运用abaqus网格划分模块对其进行网格划分，最终得到的单元数为42 192个，节点数为21 760个。金属硬密封的接触属性为“硬”接触，应尽可能使用六面体一阶单元，本次分析单元类型为C3D8I(六面体非协调模式一阶单元)，有限元网格如图5所示。

图5　有限元模型

3.3边界条件及加载

为了防止分析过程中发生刚性位移，在阀体的一端施加X、Z向位移边界条件，阀体底部施加Y向位移边界条件，如图5所示。阀门关闭状态，蝶板正面为介质水，背面为空载，在阀门的正面内腔施加压力载荷，如图6所示。

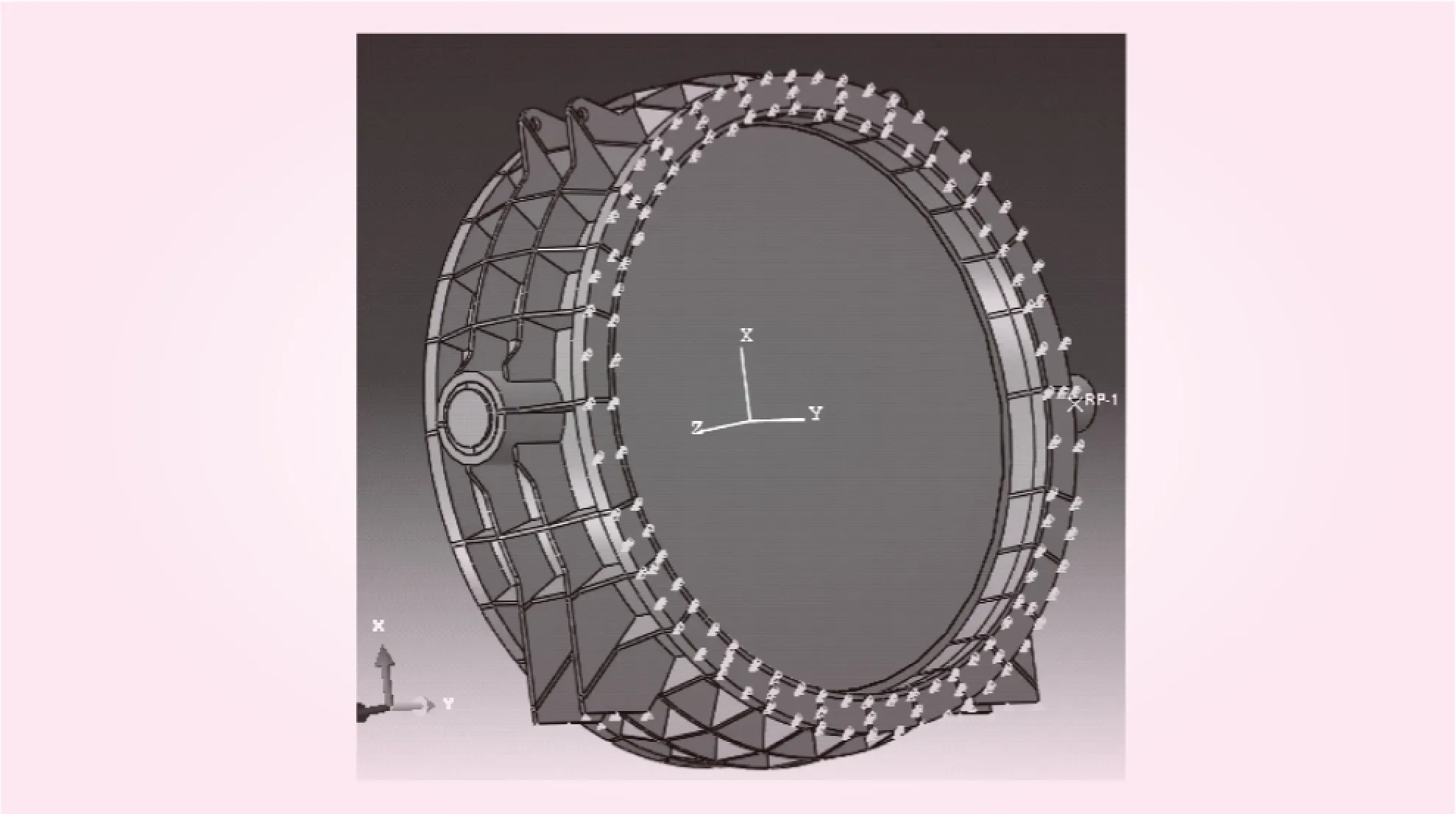
图6　边界条件

3.4接触定义

分析中接触包括阀杆与阀体接触、阀杆与蝶板的接触以及阀座与蝶板的密封面接触。由于阀杆与阀体、蝶板的接触不是分析的重点，为了减少计算量以及提高收敛速度，将其定义为绑定接触。密封面的接触定义为面-面接触，其中阀座锥面为主面，蝶板锥面为从面。

4　计算结果及分析

4.1计算结果

通过大量的仿真实验得到了阀门密封面的密封比压值和接触状态，本文只呈现了轴向偏心b=240 mm，径向偏心a=36 mm，角偏心θ=10°的分析结果，如图7、8所示。

图7　加载

图8　密封面密封比压

图9　密封面接触状态

从图7可以看出，密封面的最大比压值为217 MPa，位置为靠近阀杆处，密封面底部的比压值为150 MPa，密封面顶部的比压值为0，从中间向上下两端，比压值逐渐减小；由图8可知，密封面顶部1/4出现了间隙，最大值为0.34 mm，其他部位全部接触。

4.2分析结果与理论计算及实际情况对比分析

蝶阀关闭时主要受力部件为阀杆，密封面最大比压出现在阀杆附近，这与阀门的实际结构相吻合。由于密封面为偏心圆锥面，并且底部锥面与管道轴线的夹角最大，顶部锥面与管道轴线的夹角最小，导致顶部的密封比压为0，并且产生间隙，而底部密封面接触良好，这与实际工作中阀门顶部最易泄露相吻合。平均比压125.25 MPa，理论比压118.41 MPa，误差为5.78%，在误差范围之内。分析结果和理论经验值及实际情况的对比分析证明了分析方法是合理的。

4.3偏心值对密封性能的影响

上诉分析表明，偏心角等于锥面顶角的一半，导致顶部接触面在静水压力下法向方向不受力，比压值很小，不能实现密封。保证蝶阀能正常启闭，分别改变轴向偏心、径向偏心和角偏心采用以上相同的分析方法，进行大量的仿真实验得到了密封比压的分布规律，如表1、2、3所示。

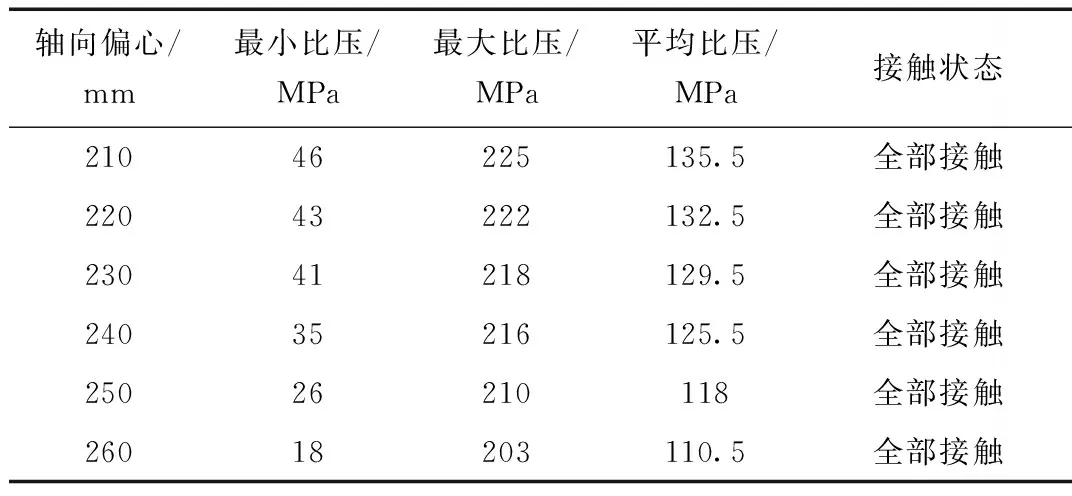
表1　比压值随轴向偏心的变化规律(径向偏心a=36 mm，角偏心θ=8°)

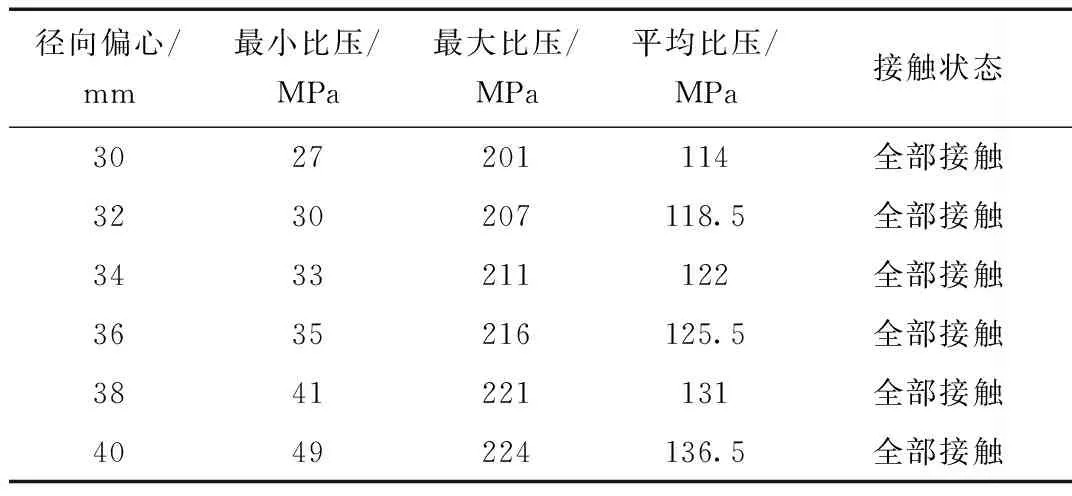
表2　比压值随径向偏心的变化规律(轴向偏心b=240 mm，角偏心θ=8°)

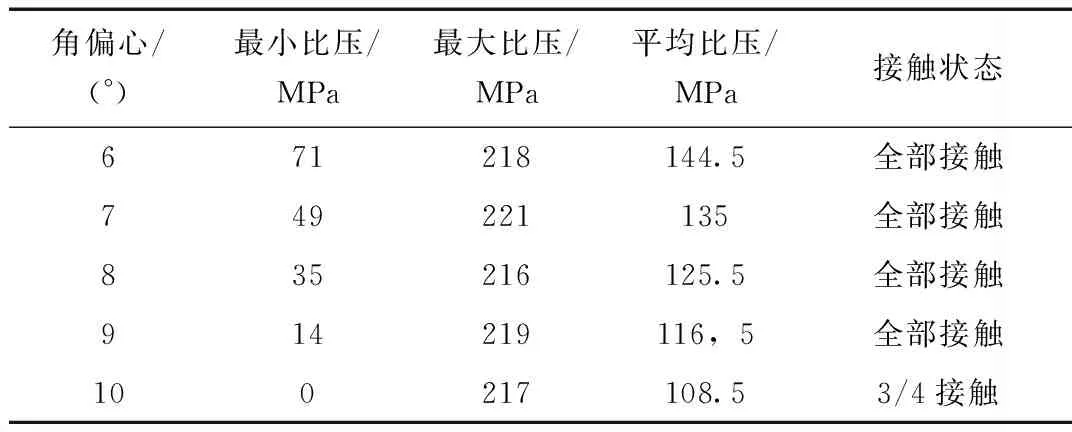
表3　比压值随角偏心的变化规律(径向偏心a=36 mm，轴向偏心b=240 mm)

径向偏心a=36 mm，角偏心θ=8°，改变轴向偏心值得到密封面的比压值和接触状态，如表1所示。从表1可知：改变轴向偏心，密封面均全部接触，密封比压值随轴向偏心值的增大而减小，不利于密封。

轴向偏心b=240 mm，角偏心θ=8°，改变径向偏心值得到密封面的比压值和密封面的接触状态，如表2所示。从表2可知：改变径向偏心，密封面均全部接触，密封比压值随径向偏心值的增大而增大，有利于密封。

轴向偏心b=240 mm，径向偏心a=36 mm，改变角偏心值得到密封面的比压值和密封面的平均位移，如表3所示。从表3可知：最小密封比压值随角偏心值的增大而减小，当偏心值等于锥顶半角时，最小比压值为0，角偏心对最大密封比压值的影响不大。

3个偏心值对蝶阀的密封性能均有影响。密封比压随轴向偏心增大而减小，随径向偏心增大而增大，二者对密封比压的影响是相互矛盾的。径向偏心的增大有利于密封，但偏心值增大将导致蝶阀的体积变大，并且增大启闭力矩。角偏心对蝶阀密封面最小比压影响明显，较大的角偏心值将导致蝶阀密封面比压值为0，从而不能实现密封。

5　结　论

针对某大型水电站DN3400三偏心蝶阀，首先运用传统的经验公式对其金属密封面的密封比压进行理论计算。然后利用solidworks三维软件建立了蝶阀的数学模型，并通过abaqus有限元分析软件对密封面的比压和接触状态进行了有限元模拟。得到了以下结论：

(1)传统经验公式计算结果和分析计算结果的误差为5.78%，分析结果与蝶阀运用中的实际情况相符合，说明了本文的分析方法是合理的。

(2)轴向偏心和径向偏心值对密封比压的影响是相互矛盾的，本文找到了它们的影响规律。

(3)当蝶阀的角偏心接近锥顶半角时，蝶阀上端的密封比压将很小，甚至没有，这将导致蝶阀泄露。而偏心角对蝶阀密封面的最大比压值几乎没有影响。

(4)通过大量的仿真实验，得到了三个偏心值与密封性能的关系，为提高三偏心蝶阀的密封性能以及三偏心蝶阀局部结构优化提供依据。

[1]顾永泉. 机械密封比压选用原则[J]. 石油化工设备， 2000， 29(2)： 25- 36．

[2]韩国鹏， 李阳光， 王超， 等. 三偏心金属密封蝶阀蝶板密封圈结构分析与研究[J]. 阀门， 2014(2)： 39- 40.

[3]杨源泉. 阀门设计手册[M]. 北京： 机械工业出版社， 1992．

[4]郝承明. 三偏心蝶阀密封结构的分析与研究[J]. 阀门， 2001(1)： 1- 5．

[5]刘磊， 文卫兵， 王乘. 双金属密封结构的有限元分析[J]. 润滑与密封， 2001(6)： 4- 8．

[6]凡增辉， 赵熙雍， 晏红文. 基于Ansys的斜齿轮接触有限元分析[J]. 机械传动， 2010， 34(4)： 68- 70．

[7]李润方. 接触问题数值方法及其在机械设计中的应用[M]. 重庆： 重庆大学出版社， 1991.

[8]石亦平， 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京： 机械工业出版社， 2006．

[9]凌晓. 三偏心蝶阀的力矩计算及结构优化[D]. 甘肃： 兰州理工大学石油化工学院， 2011．

[10]童成彪. 蝶阀的优化设计和流场研究[D]. 长沙： 湖南大学机械与运载工程学院， 2010．

(责任编辑高瑜)

Research of Hydropower Master Triple Eccentric Butterfly Valve Sealing Based on Abaqus

HE Qingzhong, WANG Yuhao, WANG Jia, LI Mingyu

(College of Mechanical Engineering, Sichuan University of Science & Engineering, Zigong 643000, Sichuan, China)

In view of the problems about triple eccentric butterfly valve (DN3400) in actual operation, the sealing performance of valve is analyzed by using Abaqus software. Compared the analysis results with traditional experience calculation and actual problem, the analysis method is proved to be reasonable. Through changing three eccentric values of triple eccentric butterfly valve, a large number of simulation results are obtained and the relationship between different eccentric values and sealing performance is founded. The results provide a theoretical basis for improving the sealing performance of large triple eccentric butterfly valve．

butterfly valve; Abaqus software; eccentricity value; sealing performance

2015- 08- 20

2014年自贡市重点科技计划项目(2014JZ05)；四川理工学院研究生创新基金(y2013012)

何庆中(1962—)，男，四川富顺人，教授，研究方向为机械设计及其相关特种设备结构特性分析与优化；王渝皓(通讯作者)．

TK7

A

0559- 9342(2016)05- 0090- 05