基于商函数的动态载荷识别最优正则化参数选取方法
2016-09-07于开平
高 伟, 于开平, 林 宏
( 1. 哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001; 2. 北京宇航系统工程研究所,北京 100076 )
基于商函数的动态载荷识别最优正则化参数选取方法
高伟1, 于开平1, 林宏2
( 1. 哈尔滨工业大学 航天学院,黑龙江 哈尔滨150001;2. 北京宇航系统工程研究所,北京100076 )
为解决载荷识别反问题,研究选取最优正则化参数商函数方法。利用Tikhonov正则化方法的最优化问题的最小二乘解,定义以正则化参数为自变量的商函数;根据不同的正则化参数,使用二次规划理论,求解Tikhonov正则化方法的最优化问题的最优解;基于不同最优解对应商函数的不同特点,将最优正则化参数的商函数方法,与广义交叉检验(Generalized Cross-Validation, GCV)准则所得载荷识别结果进行比较。数值仿真及试验验证结果表明,商函数方法对于共振区及非共振区下载荷识别问题具有较好的合理性和适用性。
载荷识别; 不适定问题; 正则化方法; 二次规划; 形函数
0 引言
载荷识别和系统辨识是反问题理论中的两类问题[1-3]。Tikhonov正则化方法[4]利用引入的正则化参数构造正则化算子,能够有效克服由系统矩阵的病态性引起的载荷识别不适定问题。最优正则化参数的选取是载荷识别理论中主要的研究方向之一,主要的正则化参数选取方法有岭迹法[5]、拟最优准则[6]、广义交叉检验准则(Generalized Cross-Validation,简称GCV)[7]、Morozov偏差原理[8]、启发式规则(Heuristic rules)[9]和L曲线(L-curve)准则[10]。正则化参数选取主要分为先验策略和后验策略两类,后验策略不需要事先知道最优正则化参数的先验信息。广义交叉检验准则和L曲线准则作为后验策略是工程上最常用的两种最优正则化参数选取方法,工程应用结果[11]表明两种方法具有更好的适应性。L曲线准则没有收敛性证明,并且有人给出L曲线非收敛的反例[12]。L曲线方法需要对应不同正则化参数的坐标点画出对数尺度下的L形曲线,坐标点过少时易导致结果精度低,坐标点过多时易导致计算量过大;在个别情况下,L曲线呈现凹形曲线[13],给曲线的最大曲率位置确定带来困难。虽然在理论上已经证明GCV准则的收敛性,但是有时用来确定最优正则化参数的GCV函数曲线过于平坦,导致确定GCV函数的最小值出现困难[14]。
笔者研究一种基于二次规划理论的确定最优正则化参数的商函数方法。它属于后验策略方法,不需要事先知道结构响应中的噪声水平。数值仿真及试验验证表明,商函数方法对于共振区及非共振区下载荷识别问题具有较好的适应性。
1 正则化方法
离散系统方程的建立基于Duhamel积分:
(1)
的离散化。将载荷作用时间区域离散化为Q个长度为Δt的时间单元,将真实载荷f(t)用最小二乘近似函数表示[15],设时间域内局部支撑域Ω内包含S-1时间单元(共S点),则支撑域Ω内形函数向量为
(2)
取Ω内中间时间单元近似载荷作为真实载荷的最优最小二乘近似,设S=2l,定义首个时间单元中形函数为
(3)
可以将所有时间单元上近似载荷表示为
(4)
则整个时间域上最小二乘近似载荷为
(5)
将式(5)代入式(1)并整理有
(6)
式中:fij为fi中第j分量。
再令
(7)
表示形函数Nj(t)的响应,其中j=1,2,…S。对式(6)在时间域上离散化,由关于fij的向量长度为Q+2l-1的向量得
(8)
则每个形函数对应的矩阵为
(9)
l-1 columns
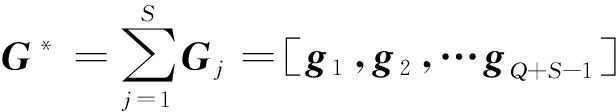
(10)
(11)
(12)
由式(10-12)得离散系统方程模型:
y=Gf,
(13)
式(13)中系统矩阵往往是病态的。
正则化方法能够有效克服系统矩阵的病态导致的不适定问题,主要思想为考察最优化问题:
(14)
式中:α为常数,α>0;‖·‖为欧氏范数。式(14)的最小二乘解表达式为
(15)
式中:I为单位矩阵。将响应y=yture+ynoise及系统矩阵G的SVD (Singular Value Decomposition)分解[12]并代入式(15):
(16)
通过对正则化参数α进行合理取值,使得识别载荷fα兼顾数值反演的稳定性和与真实载荷误差的可控性。
在载荷识别问题的正则化求解过程中,采用不同的最优正则化参数选取方法,将得到不同的最优正则化参数,以及不同精度的识别结果。由式(16)可知,较小的正则化参数可以保留更多响应ytrue的初始信息,并且更接近真实系统。在识别结果精度相同的情况下,能够得到较小最优正则化参数的最优正则化参数选取方法在实际工程中具有更好的适用性。
2 最优正则化参数选取方法
利用二次规划算法[16-18]求解最优化问题(14),矩阵GTG+α2I在参数α较大时为非病态,求解得到的识别载荷具有非常高的精度且满足式(15),整理有:GTy-GTGfα=α2fα,等式两边取欧氏范数有‖GTy-GTGfα‖=α2‖fα‖。随着常数α逐渐减小,矩阵GTG+α2I从非病态逐渐变为具有较弱的病态性,识别载荷具有较好的精度,则等式退化为‖GTy-GTGfα‖≈α2‖fα‖;如果参数α继续减小,则矩阵GTG+α2I的病态性较强,识别载荷精度非常差,则有‖GTy-GTGfα‖≠α2‖fα‖。设商函数H(α)为
(17)
商函数方法实现步骤:
(1)由SVD分解得到系统矩阵的最大奇异值σ1,给出初始参数向量α1=[σ1/50,2σ1/50,…σ1];
(2)对于向量α1中每个分量,计算相应H(α)函数值构成的向量H=[H(σ1/50),H(2σ1/50),…H(σ1)];
(3)给出阈值eop,如果H中所有分量与1的距离均不大于阈值eop,则更新参数向量α2=α1/2;
(4) 重复步骤(2)和(3),直到向量H中出现某个分量(假设为第q个)与1的距离大于阈值eop,并且接下来有连续多个分量(可取5个)与1的距离不大于eop时,假设参数向量αi=α1/2i-1,确定的最优正则化参数即为向量αi中的第q+1个分量。
3 数值仿真
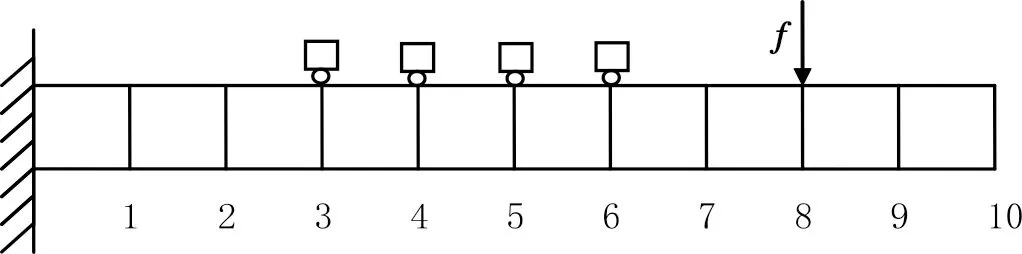
图1 悬臂梁有限元模型Fig.1 The finite element model of cantilever beam structure
采用悬臂梁有限元模型模拟钢制悬臂梁结构(见图1)。悬臂梁划分为10个单元,从左到右依次为节点1到10。
钢制悬臂梁结构的一阶固有频率为9.3 Hz,采用数值仿真分别研究悬臂梁结构在非共振区及共振区的载荷识别问题。取基函数向量为q(t)=[1,t,t2]T,即R=3,采样点个数S=4[15]。确定式(15)形式的形函数,构造y=Gf形式的离散系统方程,并利用正则化方法求解。分别使用商函数方法及GCV方法确定最优正则化参数,并比较商函数及GCV方法的结果。
3.1单输入单输出(SISO)系统载荷识别
在节点8处施加载荷,采样频率Fs=1 000 Hz,使用节点5处的加速度响应识别载荷,取阈值eop=10-4,对响应数据添加噪声:
(18)
式中:y为用于载荷识别的加速度响应;ycal为通过有限元模型计算得到的加速度响应;lp为噪声水平;noise为与ycal相同长度的均值为0、方差为1的白噪声序列;std(·)为标准差。
识别载荷与真实载荷freal之间相对误差为
(19)
3.1.1SISO系统非共振区载荷识别
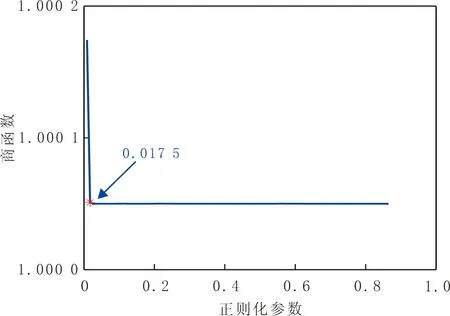
图2 SISO系统在2%噪声水平下商函数Fig.2 QF under 2% noise level of SISO system
施加正弦载荷f1(t)=40sin(40πt),作用时间为0.30 s,分别在2%及5%噪声水平下利用正则化方法识别载荷,利用商函数方法确定最优正则化参数。在2%噪声水平下商函数曲线见图2,其中星号处为最优正则化参数对应坐标点。由图2可知,当α≥0.017 5时,几乎所有函数值为1;当α<0.017 5时,函数值与1相差非常大,因此最优正则化参数α=0.017 5。在2%噪声水平下商函数及GCV方法的识别载荷见图3,在2%和5%噪声水平下商函数及GCV方法的非共振区识别结果见表1。由图3可知,两种方法的识别载荷与真实载荷拟合结果较好。
3.1.2SISO系统共振区载荷识别
施加正弦载荷f2(t)=40sin(20πt),作用时间为0.40 s。分别在2%及5%噪声水平下利用正则化方法识别载荷,利用商函数方法确定正则化参数。在2%噪声水平下商函数及GCV方法的识别载荷见图4。在2%和5%噪声水平下商函数及GCV方法的共振区识别结果见表2。
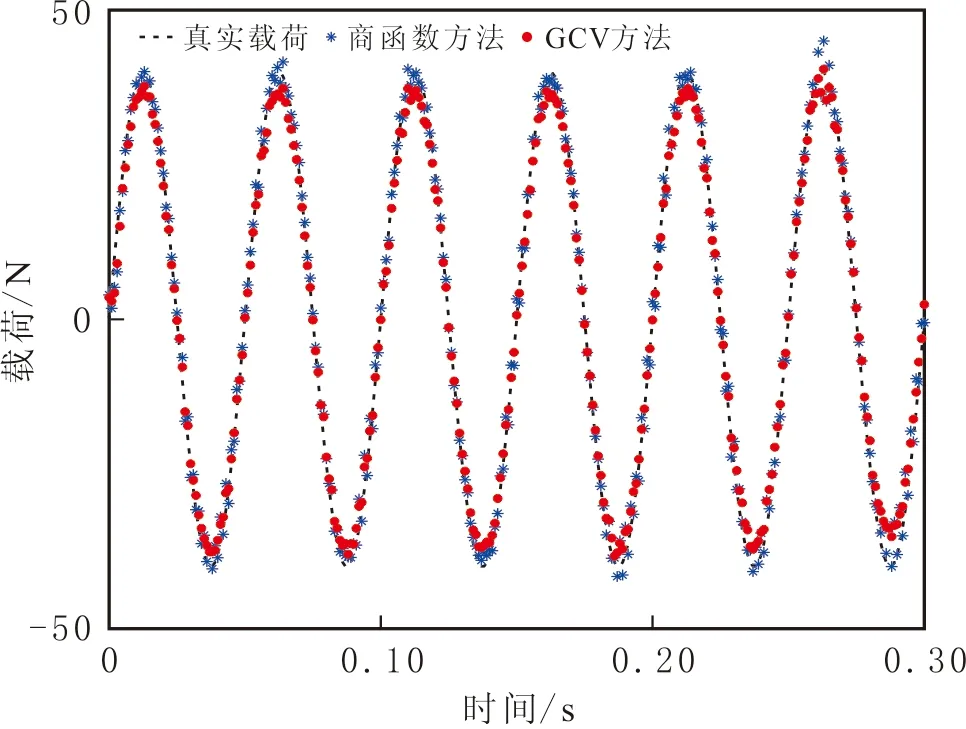
图3 SISO系统在2%噪声水平下识别载荷f1Fig.3 Identified load f1 under 2% noise level of SISO system
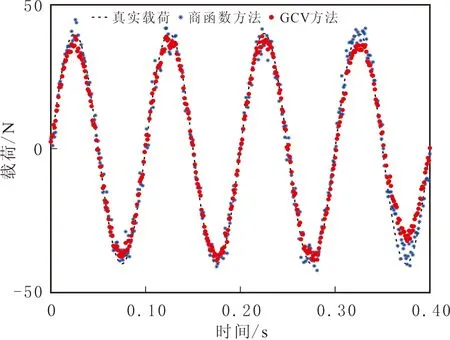
图4 SISO系统在2%噪声水平下识别载荷f2Fig.4 Identified load f2 under 2% noise level of SISO system
Table 1 Results of load identification in the non-resonant region of SISO system
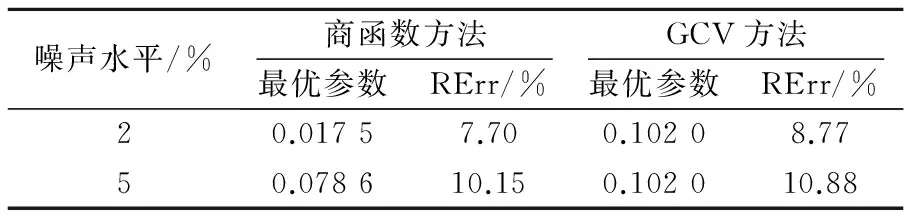
噪声水平/%商函数方法GCV方法最优参数RErr/%最优参数RErr/%20.01757.700.10208.7750.078610.150.102010.88
表2SISO系统共振区载荷识别结果
Table 2 Results of load identification in the resonant region of SISO system
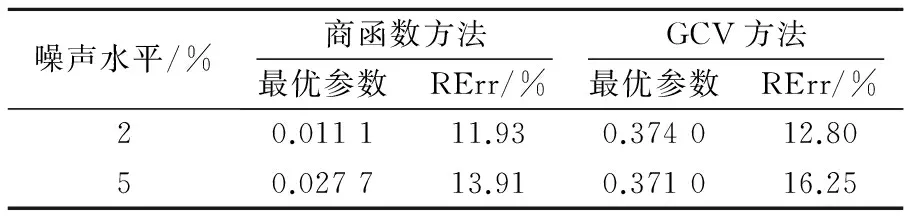
噪声水平/%商函数方法GCV方法最优参数RErr/%最优参数RErr/%20.011111.930.374012.8050.027713.910.371016.25
由图4可知,两种方法的识别载荷能较好地反映真实载荷的时间历程。由表1和表2可知,商函数方法对SISO系统载荷识别结果的噪声有较好的适应性。在零初始条件下,结构在周期激励作用下的响应中包含稳态周期项及过渡衰减项。在共振区响应中,过渡衰减项初始时刻的幅值较大,到达稳态需要的时间较长;与非共振区载荷识别结果比较,共振区识别载荷精度相对较差,同时造成对测量响应中测量噪声有较大敏感性。
3.2多输入多输出(MIMO)系统载荷识别
使用与SISO系统载荷识别情形下相同的初始条件,分别在节点8和节点6处施加正弦载荷及冲击载荷,利用半正弦波模拟冲击载荷[19],采样频率Fs=1 000 Hz。高水平的噪声对MIMO系统载荷识别结果有较大影响[20],其中冲击载荷的主要特征为最大幅值[21],对应的RErr指的是识别载荷最大幅值与真实载荷最大幅值之间的RErr。
3.2.1MIMO系统非共振区载荷识别
施加正弦载荷f1(t)=40sin(40πt),作用时间为0.25 s;冲击载荷为f3(t)=45sin(100πt),取0.16~0.17 s时间段上长度为0.01 s的半正弦波模拟冲击载荷,冲击载荷时间历程为0.25 s。使用节点7和节点9处的加速度响应,分别在1%和2%噪声水平下识别载荷。在1%噪声水平下利用GCV方法确定最优正则化参数,对应识别载荷见图5。由图5可知,冲击载荷识别效果很好;正弦载荷识别精度非常差,最优正则化参数过大导致丢失过多的系统信息。
与SISO系统载荷识别结果比较,MIMO系统载荷识别对应式(13)中方程的系统矩阵具有更高的阶数及更强的病态性。降低对商函数值近似为1的标准,在MIMO系统载荷识别过程中阈值为eop=10-2。在1%噪声水平下商函数方法识别载荷见图6。在1%和2%噪声水平下商函数及GCV方法的非共振区识别结果见表3。由图6可知,识别载荷较好地反映真实载荷的时间历程。

表3 MIMO系统非共振区载荷识别结果
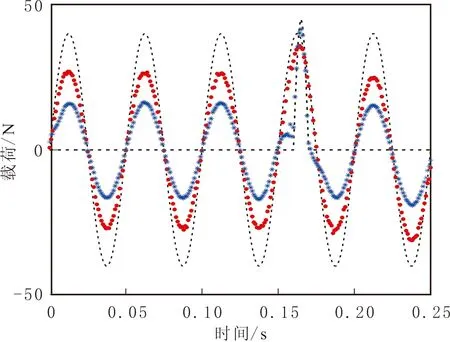
图5 MIMO系统非共振区在1%噪声水平下GCV方法识别载荷Fig.5 Identified load of the GCV method under 1% noise level in the non-resonant region of MIMO system
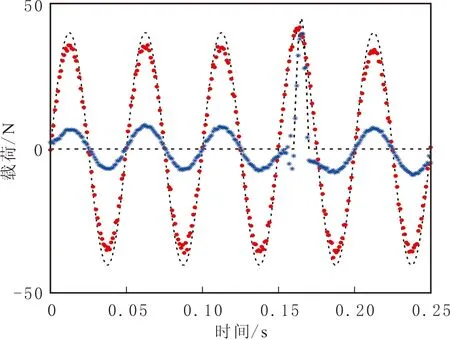
图6 MIMO系统非共振区在1%噪声水平下商函数方法识别载荷Fig.6 Identified load of QFM in the non-resonant region under 1% noise level of MIMO system
3.2.2MIMO系统共振区载荷识别
施加正弦载荷f2(t)=40sin(20πt),作用时间0.25 s;其余条件与3.2.1相同。使用节点7和节点9处的加速度响应,分别在1%和2%噪声水平下识别载荷。在1%噪声水平下利用商函数方法确定最优正则化参数,对应识别载荷见图7。在1%和2%噪声水平下商函数及GCV方法的共振区识别结果见表4。由图7可知,商函数方法的识别载荷与真实载荷的拟合结果较好。由表4可知,GCV方法确定的最优正则化参数较大,丢失过多系统信息而导致识别载荷精度较差。由表3和表4可知,商函数方法可以通过调整阈值得到满足不同系统状态的最优正则化参数,并得到精度较好的识别载荷。

表4 MIMO系统共振区载荷识别结果
4 试验验证
以钢制悬臂梁结构(见图8)作为试验模型,几何尺寸为0.900 m×0.050 m×0.009 m,弹性模量为200 GPa,密度为7.8×103kg/m3。初始条件为零,将悬臂梁结构划分为10个单元,从左至右依次为节点1至10。在节点8处施加频率为20 Hz的正弦形式载荷,并同时测量真实载荷数据,载荷作用时间为0.50 s。在节点3-6处放置加速度传感器测量结构响应,采样频率为1024 Hz。
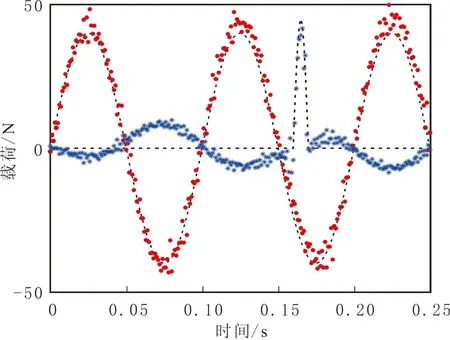
图7 MIMO系统共振区在1%噪声水平下商函数方法识别载荷Fig.7 Identified load of QFM in the resonant region under 1% noise level of MIMO system

图8 钢制悬臂梁结构Fig.8 The cantilever beam structure
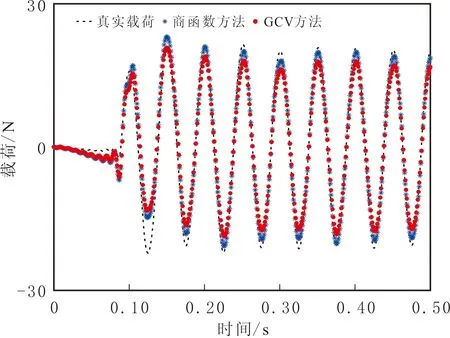
图9 试验验证识别载荷Fig.9 The identified load in the experimental verification
试验验证使用与数值仿真离散系统方程形式相同的式(13),使用节点6处加速度响应,分别利用商函数及GCV方法进行载荷识别,并与真实载荷进行比较(见图9)。
商函数方法确定的最优正则化参数及识别载荷RErr分别为α=0.109 0及15.74%,GCV方法确定的最优正则化参数及识别载荷RErr分别为α=0.202 0及19.98%。由于GCV方法确定的最优正则化参数相对较大,在载荷识别过程中丢失较多系统信息;商函数方法确定的识别载荷与GCV方法确定的识别载荷比较,具有较高的精度,并且与真实载荷吻合较好。
5 结论
(1)商函数方法属于后验策略型方法,在共振区及非共振区下载荷识别问题中能有效确定最优正则化参数,并得到高精度的识别载荷,说明商函数方法在工程上具有更好的适应性。
(2)商函数方法的判定标准基于正则化方法的最小二乘解,不会出现陷入局部最优解的问题。将商函数方法的函数值是否为1作为选取最优正则化参数的判定标准,商函数值与阈值之间容易区分,能够有效克服GCV方法最小值附近函数值过于接近而导致的确定最小值困难的问题。
(3)对于不同的实际工程需要,商函数方法可以通过调整阈值得到满足需要的最优正则化参数。
[1]文祥荣,智浩,孙守光.结构动态载荷识别的精细逐步积分法[J].工程力学,2001,18(4):117-122.
Wen X R, Zhi H, Sun S G. Highly precise direct integration scheme for structural dynamic load identification [J]. Engineering Mechanics, 2001,18(4):117-122.
[2]王晓燕,黄维平,李华军.地震动反演及结构参数识别的EKF算法[J].工程力学,2005,22(4):20-23.
Wang X Y, Huang W P, Li H J. Inversion of ground motion and identification of structural parameters by EFK [J]. Engineering Mechanics, 2005,22(4):20-23.
[3]李东升,郭杏林.逆虚拟激励法随机载荷识别试验研究[J].工程力学,2004,21(2):134-139.
Li D S, Guo X L. Experimental random loading identification using inverse pseudo excitation method [J]. Engineering Mechanics, 2004,21(2):134-139.
[4]Tikhonov A N. Solution of incorrectly formulated problems and the regularization method [J]. Soviet Mathematics Doklady, 1963,4:1035-1038.
[5]Hoerl A E, Kennard R W. Ridge regression: Biased estimation for non-orthogonal problems [J]. Technometrics, Special 40th Anniversary Issue, 2000,42(1):80-86.
[6]Kindermann S, Neubauer A. On the convergence of the quasi optimality criterion for (iterated) Tikhonov regularization [J]. Inverse Problem, 2008,2(2):291-299.
[7]Golub G H, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter [J]. Technometrics, 1979,21:215-223.
[8]Bonesky T. Morozov's discrepancy principle and Tikhonov-type functionals [J]. Inverse Problems, 2009,25(1):015015.
[9]Jin B, Lorenz D A. Heuristic parameter-choice rules for convex variational regularization based on error estimates [J]. SIAM J. Numer. Anal, 2010,48(3):1208-1229.
[10]Hansen P C, Leary D P. The use of the L-curve in the regularization of discrete Ⅲ-posed problems [J]. SIAM Journal on Scientific and Statistical Computing, 1993,14:1487-1503.
[11]Hanke M, Hansen P C. Regularization method for large-scale problems [J]. Surv. Math. 1nd, 1993,3:253-315.
[12]Vogel C R. Non-convergence of the L-curve regularization parameter selection method [J]. Inverse Problems, 1996,12:535-547.
[13]Hansen P C. The L-curve and its use in the numerical treatment of inverse problems [M]. Computational Inverse Problems in Electrocardiology, WIT Press, Southampton, 2001:119-142.
[14]Varah J M. Pitfalls in the numerical solution of linear Ⅲ-posed problems [J]. SIAM Journal on Scientific and Statistical Computing, 1983,4:164-176.
[15]Liu J, Sun X S, Han X, et al. A novel computational inverse technique for load identification using the shape function method of moving least square fitting [J]. Computers and Structures, 2014,144:127-137.
[16]Coleman T F, Li Y. A reflective Newton method for minimizing a quadratic function subject to bounds on some of the variables [J]. Siam Journal on Optimization, 1993,6(4):1040-1058.
[17]Gill P E, Murray W, Wright M H. Practical optimization [M]. London: Academic Press Inc., 1981.
[18]Gould N, Toint P L. Preprocessing for quadratic programming [J]. Mathematical Programming, 2004,100(1):95-132.
[19]Choi K, Chang F K. Identification of impact force and location using distributed sensors [J]. AIAA Journal, 1996,34(1):136-142.
[20]Li Z, Feng Z P, Chu F L. A load identification method based on wavelet multi-resolution analysis [J]. Journal of Sound and Vibration, 2014,333:381-391.
[21]Mao B Y, Xie S L, Xu ML, et al. Simulated and experimental studies on identification of impact load with the transient statistical energy analysis method [J]. Mechanical Systems and Signal Processing, 2014,46:307-324.
2015-11-13;编辑:任志平
国家自然科学基金项目(11372084)
高伟(1981-),男,博士研究生,副教授,主要从事载荷识别理论方面的研究。
于开平,E-mail: yukp@hit.edu.cn
10.3969/j.issn.2095-4107.2016.02.014
O327
A
2095-4107(2016)02-0105-07
