基于CFD的液力变矩器导轮优化设计

刘安然，石祥钟，孟 燕

(1.核工业第五研究设计院，河南 郑州450052；2.河北工程大学 水电学院，河北 邯郸 056021)



基于CFD的液力变矩器导轮优化设计

刘安然1，石祥钟2，孟 燕2

(1.核工业第五研究设计院，河南 郑州450052；2.河北工程大学 水电学院，河北 邯郸 056021)

基于CAD-CFD，分析影响液力变矩器整体性能的因素并进行优化。首先使用BladeGen对液力变矩器进行参数化造型，基于CFX软件对不同速比工况进行计算，统计液力变矩器性能变化曲线并与试验对比。分析导轮能头分布特点，并根据流场分布对导轮进行结构优化，使内、外环上导轮翼型结构分别适应不同的速比工况，最终实现对低速比工况时导轮能头损失的优化，优化后涡轮输出力矩增量最大达到175.36 N·m，液力变矩器在0速比工况下变矩比增加0.344，效率在0.274速比工况下增加2.95%。

液力变矩器；导轮；CFD；优化设计

液力变矩器应用广泛，其性能的优化提升具有重要的意义[1]。其传统设计方法一般根据束流理论进行设计[2-3]，并在大量试验的基础上根据经验进行优化改型，由于液力变矩器内部流场复杂，优化改型需要较大的投入。随着CFD的发展日益成熟为液力变矩器的研究和优化设计提供了一种实用高效的新方法[4]，并能准确的分析液力变矩器的内部流场[5-8]。本文根据束流理论设计的三元件液力变矩器，在低速比工况下导轮能头损失较大，限制整体性能的提升问题，使用WorkbenchBladeGen对某型号三元件液力变矩器进行参数化造型[9]，降低低速比工况下导轮能头损失，对液力变矩器的效率、变矩比和输出力矩进行优化。

1 液力变矩器CFD计算

1.1 几何模型

根据液力变矩器几何参数进行建模，并使用BladeGen对模型进行参数化。泵轮叶片为23个，涡轮叶片为26个，导轮叶片为17个，液力变矩器几何模型如图1。

1.2 网格划分

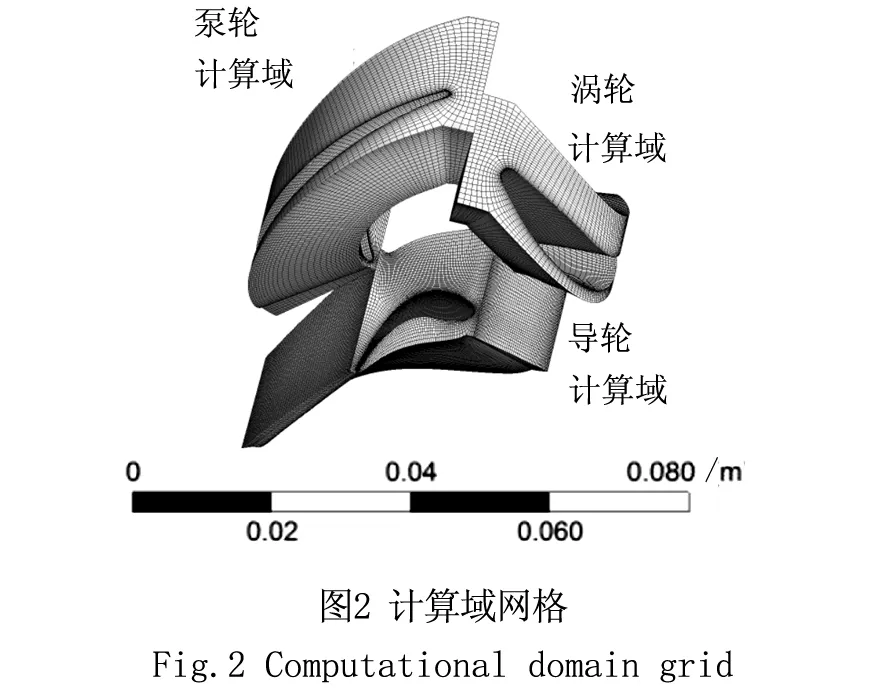
使用turbogrid分别对泵轮、涡轮和导轮进行六面体网格划分。根据液力变矩器各个元件周期性分布特点，取单周期进行计算并忽略周期间不均匀性，泵轮计算域网格单元数为109 020个，涡轮计算与网格单元数为109 417个，导轮计算域网格单元个数为172 672个，网格满足无关性要求，网格模型如图2。

1.3 三维流场数值计算

对液力变矩器进行三维流场数值计算，不考虑转动过程中内部流场的脉动，认为输入、输出转速不变的情况下内部流场处于稳态。首先将网格导入CFX中，设置计算域之间的交界面为冻结转子交界面，并根据泵轮、涡轮和导轮的个数设置啮合角的大小。内环、外环和叶片壁面均设置为无滑移壁面。根据试验工况的不同分别设置输入转速和输出转速，并根据外部供给油的压力设置液力变矩器的参考压力。

建立工作油模型并给定密度ρ为899.1 kg/m3，粘度μ为0.001 89 Pa·s，流体不可压缩。液力变矩器在实际工作过程中除工作油在内部循环流动，同时还有外部供油进行冷却并防止汽蚀，因外部供油影响较小，可忽略不计，只考虑内部油的循环。并认为在实际稳定工作过程中，油温保持不变，且循环流动过程流量保持平衡。

选择湍流计算为κ-ε模型，计算过程中同时对泵轮、涡轮和导轮的力矩和进行监视，在力矩和接近0 N·m且残差达到收敛标准时停止计算。

2 CFD计算结果分析

2.1 CFD计算结果与试验数据对比

对试验工况分别进行计算，对性能计算结果与试验数据进行对比，如图3。计算结果显示稳态计算能够较为真实的反应液力变矩器的实际工作过程，在速比为0.8以下的中、低工况时，精确度较高；在0.8以上的高速比工况时，效率偏差略大，但能正确反映变化规律。

CFD计算结果不但能准确的计算出整体性能变化，还能够方便的查看内部流场和压力分布。液力变矩器内部元件的性能共同决定了整体性能的优劣，比对内部元件单独考察，能够快速分析在不同工况下整体性能的制约因素，指明优化目标和优化方向。在产品开发的过程中，能够全面考察结构优化对流场的影响，及时发现不足并加以改进，大大节约设计成本并缩短产品开发周期。

2.2 液力变矩器性能分析

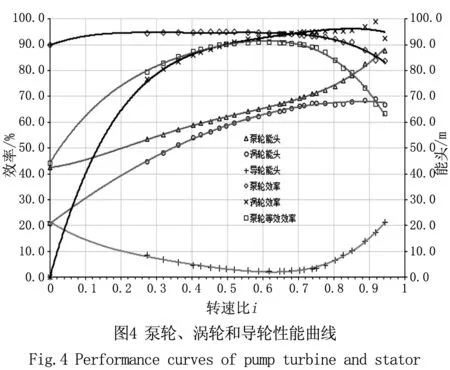
统计液力变矩器的泵轮、涡轮和导轮的能头，泵轮效率、涡轮效率以及泵轮等效效率(将导轮和泵轮综合计算得出泵轮等效效率)，结果见图4。其中能头是根据伯努利方程统计三个计算域进出口能头差，泵轮、涡轮效率则是各自输入能量与输出能量的比值。泵轮等效效率是将导轮与泵轮综合考虑，计算输入能量与输出能量的比值，泵轮等效效率乘以涡轮效率就是液力变矩器的效率。

从图4可以看出，泵轮在速比变化过程中，基本上均落在高效范围内，并且随着工况的变化，泵轮效率变化不大，性能较好。

涡轮随着速比的增大，其效率呈逐渐增大趋势，且在0.8以上的高速比范围内效率最高，而在中低速比范围内其效率偏低，说明涡轮的高效范围偏离实际运行工况。在速比达到0.9以后，涡轮内流场涡轮效率波动变大，精度降低。

由于导轮仅起到变矩的作用，其能头大小亦是损失能头大小，因此泵轮提供一定能头的情况下，导轮损失越小，则意味着涡轮可利用能头越多，因此减小导轮的能头损失，有利于提高整体的性能。观察导轮能头分布曲线，呈现两头高中间低的状态，因此该导轮在低转速比和高转速比的时候能头损失均较大，特别是在低速比工况下，导轮较大能头损失已经成为制约涡轮输出扭矩的重要因素，因此需要合理的分配涡轮的能头损失，优化液力变矩器的整体性能。

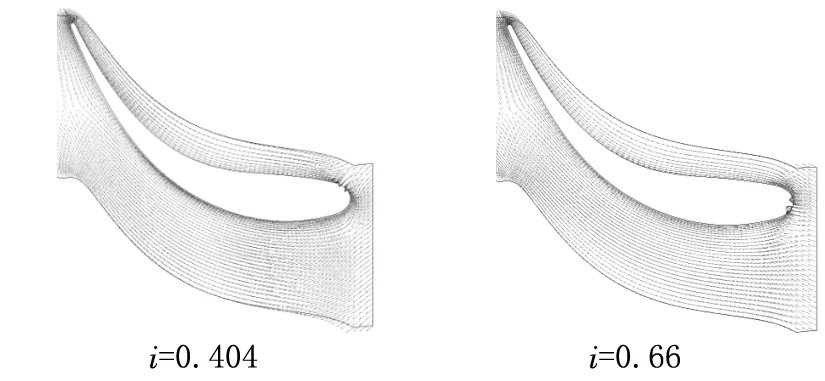
对不同速比工况下的导轮内部流场进行分析，取几组典型工况，如图5。导轮速度场显示，在低速比工况时，来流对于叶片有正冲角，并且速比越低正冲角越大，来流撞击损失和叶栅内的涡会导致导轮能头损失变大。在中速比工况下，导轮流场均匀，对应的能头损失也最小。在高速比的时候，来流相具有负冲角，更容易在流道中形成较为明显的涡流，从导轮性能头曲线上可以看出，负冲角导致能头损失增大较快。

从泵轮等效效率曲线也可以看出，导轮的能头损失也使得低、高速比工况时泵轮的等效效率降低，为了提升整体性能，特别是低速比工况时的输出力矩，需要对导轮结构进行优化。

3 导轮叶片结构优化

3.1 导轮叶片翼型优化

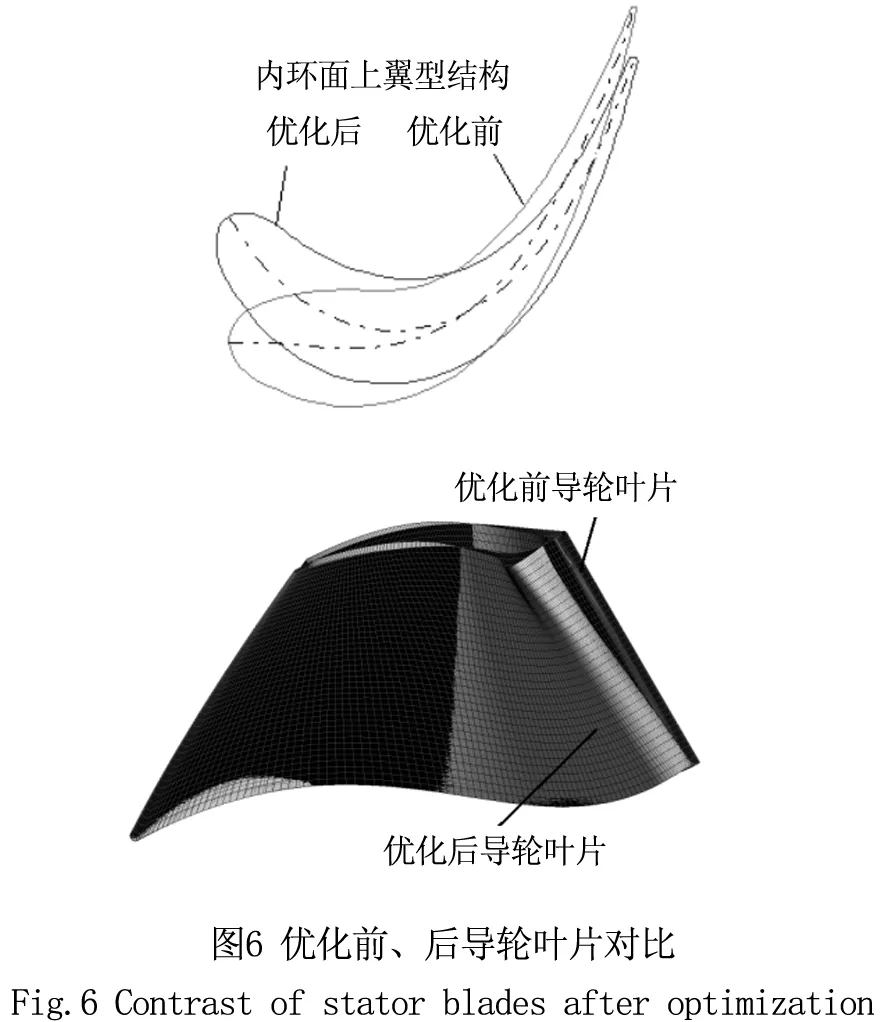
目前导轮具有高效范围窄、低速比工况时能头损失大的特点，是制约涡轮输出力矩大小的重要因素，对启动性能不利。流场分析结果显示，导轮在低转速比时，叶片整体的正冲角度均比较大，为了增强导轮对低转速比的工况的适应性，调整内环面上的翼型结构，减小翼型进口的正冲角和叶栅中的脱流损失，同时为了减少对泵轮的影响，控制翼型出流角度不变，外环面上的翼型结构保持不变。

根据导轮中速度场分布特点，调整Beta、Theta等参数的分布曲线。直到计算结果达到设计目标，对比优化前后导轮叶片结构，如图6。

3.2 导轮内部流场分析

优化后对低转速比工况进行计算，选取转速比i=0.274时的流场进行分析，从内环到外环方向取4组流面的速度矢量场，如图7。

优化后，低速比工况下，导轮靠近内环的部分流场较为均匀，撞击损失较小，无脱流；而靠近外环的部分有正冲角，具有一定的撞击和脱流。优化后内环处的导轮结构较原来叶片更为扭曲，靠近内环处的翼型结构能够较好的适应低转速比工况下的流场，而靠近外环部分的翼型结构则能较好的适应中、高转速比的工况时的流场，随着速比的增大，从内环到外环总有一部分的区域处于高效范围，从而拓宽了导轮对不同工况的适应性。

4 优化后整体性能分析

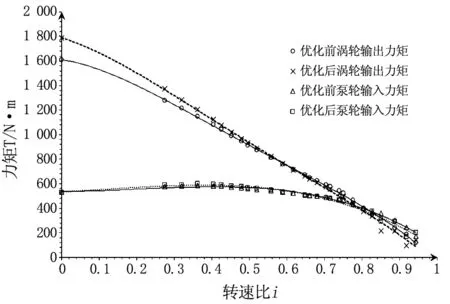
导轮优化后，计算液力变矩器的整体工作性能，统计导轮优化前后液力变矩器输入、出力矩参数，如图8。在转速比0.66以前的中低速比工况下，输出扭矩均有不同程度的增加，在转速比为0的时候转速比增加量达到最大为175.63 N·m，对应的输入扭矩变化量较小约为10 N·m。在转速比达到0.6以后的中、高转速比工况，输入、输出扭矩均不同程度的降低，输出扭矩的下降范围在30 N·m以内，变化量较小。

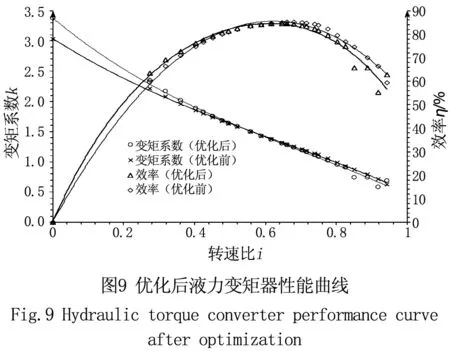
统计对比优化前、后液力变矩器的效率和变矩比，优化后液力变矩器整体性能曲线如图9。分析可知，液力变矩器在0速比工况下变矩比增加0.344，效率在速比为0.274工况下增加2.95%，改善了液力变矩器低转速比工况的性能，达到预期的设计目标，计算结果表明优化方法有效。

5 结论

1)使用CFX对液力变矩器进行数值计算，数值计算结果与台架试验结果相差较小，能够真实的反应液力变矩器内部流场状况。

2)基于传统设计方法的导轮，在偏离最优工况后能头损失增加较快，影响液力变矩器的整体性能。

3)根据数值计算结果，对内环面上翼型进行优化，减小低转速比工况下叶片的正冲角和脱流损失，而保持外环面上翼型不变，增强了导轮对不同转速比工况的适应性。

4)优化后，中低转速比工况下涡轮输出力矩得到改善，输出扭矩增加到175.63 N·m，高速比工况下输出力矩略有降低，变化值均在30 N·m范围内。

(5)液力变矩器在0速比工况下变矩比增加0.344，效率在速比为0.274工况下增加2.95%，改善了液力变矩器低转速比工况的性能，达到预期的设计目标。

(6)CAD-CFD设计方法快捷有效，能够缩短产品的开发周期并节约成本。

[1]马文星，何延东，刘春宝.液力传动研究现状分析与展望[J].农业机械学报，2008(7)：51-55.

[2]罗邦杰.工程机械液力传动[M].北京：机械工业出版社，1991.

[3]马文星.液力传动理论与设计[M].北京：化学工业出版社，2004.

[4]才 委，马文星，刘春宝，等.基于三维流场计算的液力变矩器特性预测方法[J].哈尔滨工程大学学报，2007，28(3)：316-319.

[5]石祥忠.液力变矩器内部三维流动数值模拟与特性预测方法研究[D].吉林：吉林大学，2005.

[6]吴光强，王立军.基于CFD的液力变矩器等效参数性能预测模型[J].同济大学学报：自然科学版，2013(1)：121-127.

[7]韩克非，吴光强，王 欢.基于CFD的泵轮叶栅关键参数对液力变矩器的性能影响预测[J].汽车工程，2010，32(6)：497-500.

[8]刘 城.向心涡轮式液力变矩器叶栅系统参数化设计方法研究[D].北京：北京理工大学，2015.

[9]刘安然，施 晶，石祥钟，等.基于BladeGen的混流水轮机转轮叶片优化研究[J].河北工程大学学报：自然科学版，2014，31(2)：93-97.

(责任编辑王利君)

Hydraulic torque converter stator blade optimization design based on the CFD

LIU Anran1,SHI Xiangzhong2, MENG Yan2

(1.The Fifth Research and Design Institute of Nuclear Industry, He’nan Zhengzhou 450052, China; 2.School of Water Resources and Hydropower, Hebei University of Engineering, Hebei Handan 056021, China)

Hydraulic torque converter optimization design was based on CAD - CFD, this paper analysis the influence factors to the whole performance and optimal design the hydraulic torque converter. Modeling of the hydraulic torque converter was parameterized by using BladeGen at first, the working conditions in different speed ratio were calculated by basing on CFX, statistical performance curves of the hydraulic torque was compared with experiment results. This paper analyzed the characteristics of energy head distribution, and obtained optimal structure by according to flow field, made aerofoil structure in internal and external ring adapt to the working conditions with different speed ratio, the energy head optimization of state working in low speed ration working conditions was achieved, which above increasd the turbine output torque; the maximum increment of turbine output torque at low speed rate working conditions reached to 175.36N·m. After optimization, the hydraulic torque converter torque ratio increased 0.344 with 0 speed ratio working condition,the efficiency increased 2.95% in 0.274 speed ratio working condition.

hydraulic torque converter; stator; CFD; optimization design

2016-03-28

河北省科技计划项目(12211906);河北省高等学校科学技术研究重点项目(ZH201201 5)

刘安然(1990-)，男，河南商丘人，研究生，助理工程师，从事流体机械设计与性能方面的研究。

1673-9469(2016)02-0103-05

10.3969/j.issn.1673-9469.2016.02.023

TH137.332

A