基于AGA的智能桁架结构模糊振动控制

张京军，段瑶瑶，高瑞贞

(1.河北工程大学 机电工程学院，河北 邯郸 0560382；河北工程大学 土木工程学院，河北 邯郸056038)



基于AGA的智能桁架结构模糊振动控制

张京军1，段瑶瑶2，高瑞贞1

(1.河北工程大学 机电工程学院，河北 邯郸 0560382；河北工程大学 土木工程学院，河北 邯郸056038)

应用一种根据适应度自动调整选择交叉概率和变异概率的自适应遗传算法(Adaptive Genetic Algorithm，简称AGA)，来优化智能桁架结构模糊控制系统。首先，考虑到压电主动杆的机电耦合特性，建立系统的有限元动力方程；其次，以智能桁架结构的主动杆轴向位移差为优化目标，使用自适应遗传算法优化模糊控制规则，以增强智能桁架结构模糊控制器的振动控制效果；利用Matlab/Simulink建立空间智能桁架结构的仿真模型，对模糊规则优化前后的控制结果进行对比。仿真结果表明：使用自适应遗传算法优化后的模糊控制器，能够加快智能桁架振动衰减速度，并且有效消除模糊控制的稳态误差。

自适应遗传算法；智能桁架；模糊规则；主动振动控制；Matlab

大型空间智能桁架结构在航空航天领域广泛应用，这类结构具有低刚度、弱阻尼比、低固有频率等特性[1]，并且在太空的真空状态下，一旦发生振动将很难衰减，这样不但会给航天器的工作造成很不利的影响，也可能导致结构的疲劳破坏[2]。因而对大型空间智能桁架的振动控制进行研究有重大意义[3]。一般的控制方法主要有自适应控制，鲁棒控制和最优控制等[4]，这些都需要建立智能桁架结构精确的数学模型。模糊控制方法不要求控制对象精确的数学模型[5]，鲁棒性和适应性较强，适合控制空间智能桁架这类复杂的控制对象，郝莉红将其应用于汽车悬架控制系统中[6]。遗传算法是一种全局搜索算法，可以用于寻找复杂问题的最优解，乔晓艳等将其用于电力系统负荷模型准确度研究中[7]，遗传算法同样可以用于模糊规则的寻优问题[8-9]。本文将自适应遗传算法和模糊控制相结合，通过优化模糊控制器的控制规则，有效控制桁架结构的振动。

1 建立桁架结构有限元模型

设柔性桁架结构中共有nc个压电主动杆，作动器和传感器都布置于同一根杆上，建立智能桁架结构机电耦合有限元模型[3]:

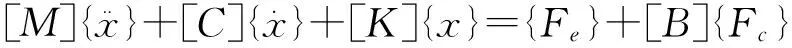
(1)

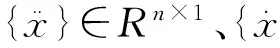
由于对于实际的物理模型，高频的振型有较大的阻尼，并且不容易被激起，即便被激起也可以在较短的时间内得到停止，因此低阶模态更为重要，为降低模型维数，采用模态截断处理，即保留低阶模态，忽略高阶模态。

在受控的低阶模态子空间内，将各阶模态分离出来实现独立模态控制：

(2)

式中fci为第i模态控制力，i=1,2,…,nc；Φi为第i列矩阵的Φ；fe为桁架结构的外部节点力向量。

2自适应遗传算法优化模糊规则

2.1空间智能桁架结构模糊振动控制器设计

本文中智能桁架采用压电主动杆，每个主动杆中都有一个作动器和一个传感器，为每一个主动杆上设置一个模糊控制器，各个模糊控制器之间独立工作，各自从传感器获得输入信号，通过模糊规则转化为输出信号，实现对整个结构的振动控制。

(1)输入变量和输出变量的选择

智能桁架的主动杆上的力传感器输出信号为主动杆轴向力，由于轴向力包含作动力项，使其存在虚假控制的可能性[3]，因而主动杆轴向力不能直接作为模糊控制器的输入，在本文中，压电主动杆两端节点的轴向位移差及其变化率作为模糊控制器的输入信号e和ec，控制反力为其输出信号u。

输入量通过量化因子转化为一定范围内的量化值，选择三角形(trimf)和梯形(trampf)型隶属函数为输入量的隶属函数，论域为{-8，-7，…0，…7，8}。输出量则通过比例因子转化到一定的论域范围内，论域为{-6，-5，…0，…5，6}，输出量选择三角形(trimf)型隶属函数。输入量误差及误差变化率以及输出量控制反力模糊语言变量的词集均为：负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)。

(2)模糊规则

模糊规则体现了输入变量和输出变量之间的关系。本文采用双输入单输出的模糊控制器，两个输入量分别有7个模糊子集，这样构成49条模糊控制规则：

Rule:if e is eiand ec is ecj,then u is uij

其中，1≤i≤7,1≤j≤7。

模糊推理方法采用Mandani法，而清晰化方法则采用重心法。

2.2改进的自适应遗传算法优化模糊控制规则

模糊规则是模糊控制器的核心部分，模糊控制器的控制效果受到模糊规则变化的影响。图1所示两个模糊规则不同的模糊控制器控制下的结构动态响应图。

该模糊控制器输出有7个模糊子集，而每条模糊控制规则有7种可能，则49条模糊控制规则有49种不同的方案，若使用传统的优化方法不易得到最优解，本文使用一种新的改进的自适应遗传算法搜索最优解，能够得到很好的效果。

(1)初始种群的确定

按照模糊控制规则表中语言变量的个数，将最优解的分布范围限定在1～7，并在该分布范围内随机生成规模为100的初始种群，且在遗传算法的迭代过程中，种群规模不发生变化。

(2)模糊规则编码

本文将对模糊控制规则进行十进制编码，用数字集{1，2，3，4，5，6，7}来表示模糊语言集{NB，NM，NS，ZE，PS，PM，PB}，把模糊控制规则变为数值形式，并将其展开成一维形式，形成遗传算法所需要的染色体，如图1中模糊控制规则1则表示为{777764477776446666433666432255422224421111441111}，图1中随机生成的模糊规则2表示为{3326244236314324137551721414442551427215346474553}。

(3) 适应度函数的选取

本文以智能桁架结构的主动杆轴向移差作为遗传算法的目标函数，表达式为：

J(x)=Abs(max(x))

(3)

但是由于遗传算法的要求是个体适应度越大则结构越是最优，因此需将目标函数转化为最大值问题，此转换函数为：

(4)

(4)改进的自适应遗传算法

自适应遗传算法是具有比例选择，自适应交叉和变异操作的遗传算法的总称。个体的适应度在种群中的平均适应度和最大适应度之间进行调整，而交叉概率Pc和变异概率Pm能够随着这些变化而改变[10]，当个体的适应度越接近最大适应度时，Pc和Pm越小；当个体适应度值趋近于最大适应度值时，Pc或Pm趋近于零，这样就能够采用相对某个解得最佳Pc和Pm。因此自适应遗传算法不但能维持种群的多样性，而且还能够确保遗传算法的收敛性[11]，但是该算法比较适用于进化的后期，对于进化的初期很不利。

本文应用一种新的自适应遗传算法，根据适应度值来调Pc和Pm[12]。Pc和Pm按如下公式进行调整。

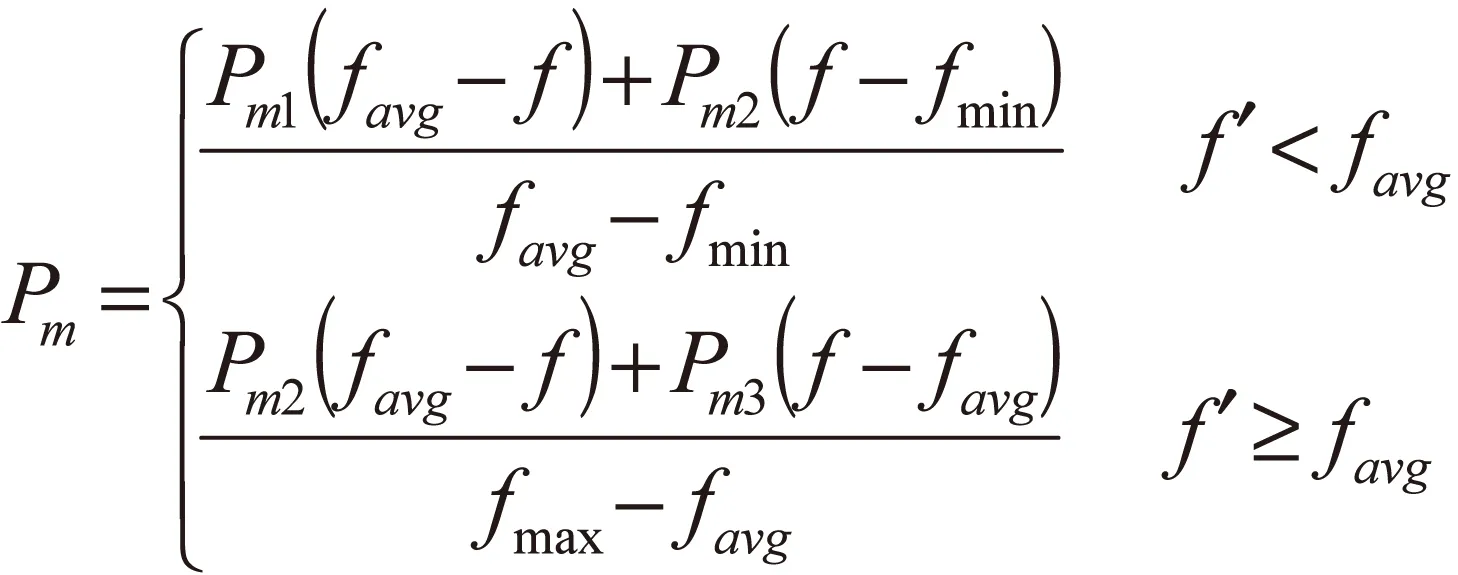
(5)

(6)

式中：fmax为种群个体适应度值中最大值；favg为每代种群的适应度值的平均值；fmin为种群个体适应度值的最小值；f′为要交叉的两个个体适应度值较大者；f为要变异个体的适应度值；Pc1>Pc2>Pc3，Pm1>Pm2>Pm3，并且交叉概率和变异概率取值区间为(0，1)，可在优化过程中调整。

本文改进的自适应遗传算法，是根据适应度值的集中程度，以种群为单位，自适应地改变种群的Pc和Pm，使它们能够随着种群中每个个体的适应度值在种群的最大适应度、平均适应度和最小适应度之间进行调整。例如，当要交叉的个体中适应度较大的个体，其适应度值比种群平均适应度值小时，则其值应该在平均适应度值和最小适应度之间进行调整，对于变异概率，亦是同理。

改进后的Pc和Pm不但能随适应度改变而改变，而且种群中优良个体的Pc和Pm也得到了提高，在搜索中有效保留了优良个体，增强了较差个体的变异能力，使算法不局限于局部最优解，有效避免早熟现象。自适应遗传算法流程图见图2：

(5)选择操作

本文采用轮盘赌算法[13]，即个体被选中的概率与其适应度值成正比，设种群大小为n，个体i的适应度为fi，则个体被选择的概率psi为：

(7)

(6)交叉操作

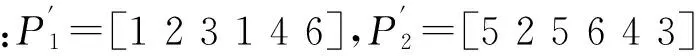
(7)变异运算

3 系统模型仿真试验及结果分析

本文所选择的智能桁架结构模型，由普通杆和主动杆组成，该桁架结构尺寸为 0.2 m×0.2 m×1.2 m，由83根杆件组成，普通杆件采用铝合金材料，主动杆粘贴压电陶瓷(PZT)材料作为压电片。传感器、驱动器同时布置于固定端根部的1根主动杆件上。该桁架结构的前4阶模态阻尼比都为ξ=0.03，智能桁架顶部节点受到大小500 N，作用时间为0.01 s的瞬态激励，桁架结构的基本参数表见表1。

表1 空间桁架结构参数

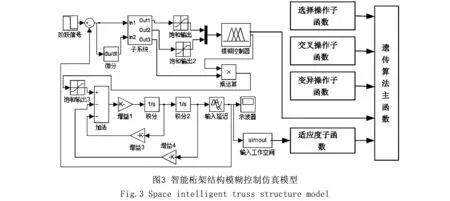
采用自适应遗传算法与模糊控制相结合，建立智能桁架结构模糊控制系统的仿真模型，如图3所示，在Matlab中运行程序。本文模拟了一阶模态振型下未被优化，使用简单遗传算法及使用新的自适应遗传算法优化后的模糊控制器控制下的智能桁架结构振动响应曲线，仿真结果如图4～图5。

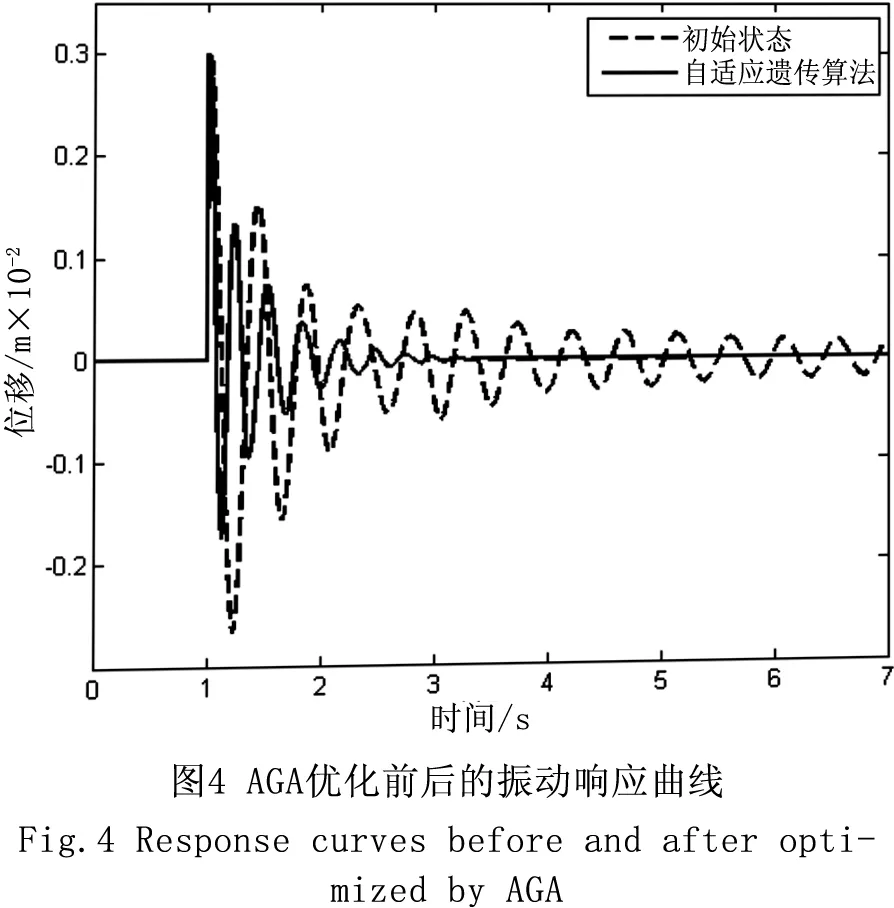
图4为未使用遗传算法优化与使用自适应遗传算法优化后的模糊控制器控制作用下智能桁架振动控制结果。由图可知，在模糊控制器未得到优化时，智能桁架的输出位移经过4 s衰减到0.02左右，但是在4 s后的控制过程中存在明显的震荡现象和稳态误差；而经过自适应遗传算法优化后的模糊控制器控制作用下，控制效果非常明显，3 s内控制结果已经基本得到抑制，没有震荡现象和稳态误差。

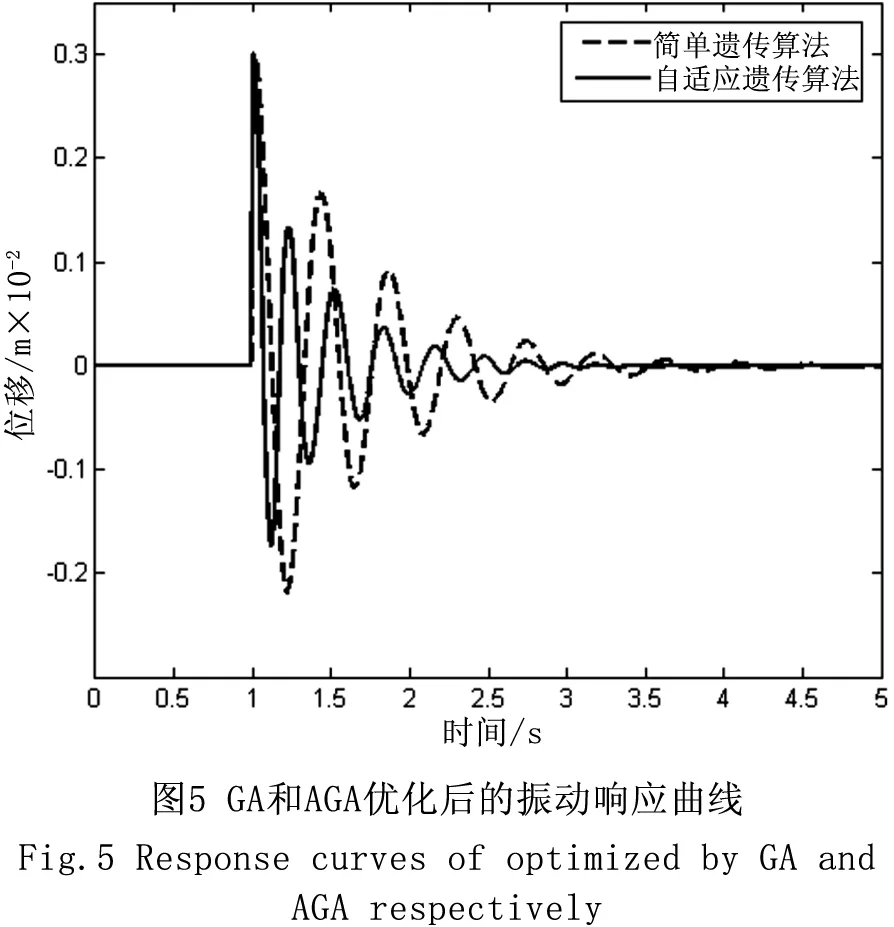
图5为简单遗传算法与自适应遗传算法分别优化模糊控制器作用下的位移输出曲线的对比。由仿真结果可以看出，简单遗传算法优化的模糊控制器完成控制所需要时间为5 s，而自适应遗传算法优化的模糊控制器能够明显加快桁架结构振动衰减，3 s内完成控制，并且有效消除简单遗传算法优化控制下的稳态误差。

4 结论

1)仿真结果表明，模糊控制规则能够影响模糊控制器对智能桁架结构的控制效果。

2)采用遗传算法优化模糊规则后，能够减少控制时间，使桁架结构振动迅速得到控制。

3)采用改进的自适应遗传算法优化模糊规则后，比简单自适应遗传算法所需要的控制时间减少40%，并能有效消除稳态误差，控制效果更好。

[1]GAO W，CHEN J J，MA H B，et al.Optimal placement of active bars in active vibration control for piezoelectric intelligent truss structures with random parameters[J].Computers & Structures，2003，81(1)：53-60.

[2]CHEN Gunshing，BRUNO，ROBIN J，et al.Optimal placement of active/passive members in truss structures using simulated annealing[J].AIAA journal，1991，29(8)：1327-1334.

[3]GUO Tieneng，LIU Zhifeng，CAI Ligang.An Improved Force Feedback Control Algorithm for Active Tendons[J].Sensors，2012，12(8)：11360-11371.

[4]KHOSHNOOD A M，MORADI H M.Robust adaptive vibration control of a flexible structure[J].ISA transactions，2014，53(4)：1253-1260.

[5]ZADEH L A.Fuzzy sets[J].Information and control，1965，8(3)：338-353.

[6]郝莉红.车辆半主动悬架FUZZY-PID控制方法研究[D].邯郸：河北工程大学，2013.

[7]乔晓艳，佘 娜，孟 鑫.基于遗传算法的电力系统负荷模型准确度研究[J].河北工程大学学报：自然科学版，2013,30(4)：78-81.

[8]PATRICK SIARRYA，FRAN OIS GUELYB.A genetic algorithm for optimizing Takagi-Sugeno fuzzy rule bases[J].Fuzzy sets and systems，1998，99(1)：37-47.

[9]KIM HYUN SU，KANG JOO WON.Semi-active fuzzy control of a wind-excited tall building using multi-objective genetic algorithm[J].Engineering Structures，2012(41)：242-257.

[10]LIN J，ZHENG Y B.Vibration suppression control of smart piezoelectric rotating truss structure by parallel neuro-fuzzy control with genetic algorithm tuning[J].Journal of Sound and Vibration，2012，331(16)：3677-3694.

[11]EMRE SUMER，MUSTAFA TURKER.An adaptive fuzzy-genetic algorithm approach for building detection using high-resolution satellite images[J].Computers, Environment and Urban Systems，2013(39)：48-62.

[12]SHOU-YI YU，SU-QIONG KUANG.Fuzzy adaptive genetic algorithm based on auto-regulating fuzzy rules[J].Journal of Central South University of Technology，2010(17)：123-128.

[13]张国强，彭晓明.自适应遗传算法的改进与应用[J].舰船电子工程，2010(1)：83-84.

[14]DE JONG K A.Analysis of the behavior of a class of genetic adaptive systems[D].Michigan :University of Michigan，1975.

(责任编辑王利君)

Fuzzy control for intelligent truss structure based on AGA

ZHANG Jingjun1, DUAN Yaoyao2, GAO Ruizhen1

(1.Mechanical and Electrical Engineering Institute. Hebei University of Engineering, HebeiHandan 056038, China; 2.College of Civil Engineering, Hebei University of Engineering, Hebei Handan 056038, China)

In this paper, an adaptive genetic algorithm (AGA) which can adaptively select crossover probability and mutation probability is presented to optimize the fuzzy control system for the space intelligent truss structure. Firstly, considering the electromechanical coupling characteristic of piezoelectric active bars, the finite element dynamic equations of the system are established. Secondly, the optimization goal is the minimum of axial displacement difference of intelligent truss active bars. An adaptive genetic algorithm is applied to optimize fuzzy control rules to improve the control effect of fuzzy controller of intelligent truss structure. To demonstrate the effectiveness of this method, the model of space intelligent truss structure is established by the Matlab / Simulink simulation, and the control results of fuzzy rules before and after optimization are compared. Simulation results show that after the optimization with adaptive genetic algorithm, the intelligent truss vibration damping rate has also been accelerated, and the steady-state error of fuzzy control are effectively eliminated.

adaptive genetic algorithm; intelligent truss; fuzzy rules; active vibration control; Matlab

2015-12-18

国家自然科学基金资助项目(11302066 和11272112)特约专稿

张京军(1963-)，男，河南虞城人，博士，教授，从事智能桁架结构振动控制方面的研究。

1673-9469(2016)02-0005-05

10.3969/j.issn.1673-9469.2016.02.002

TG333.17

A