关于斜投影乘积的若干性质

周玉兴，黄敬频，刘晓冀，涂火年（.广西师范学院 师园学院，南宁 506；.广西民族大学 理学院，南宁 50006；.广西财经学院信息与统计学院，南宁 5000）

关于斜投影乘积的若干性质

周玉兴1，黄敬频2，刘晓冀2，涂火年3
（1.广西师范学院 师园学院，南宁 530226；2.广西民族大学 理学院，南宁 530006；3.广西财经学院信息与统计学院，南宁 530003）

摘要：根据斜投影的定义及其性质，并结合空间直和分解，研究2个斜投影乘积的性质，得到若干等价命题.对于3个或多个斜投影的乘积，也有类似的结论.

关键词：斜投影乘积；直和分解；斜投影算子；投影矩阵

斜投影算子在系统识别、多变元分析、参数估计、系统建模和信号检测等领域具有广泛应用［1-3］.斜投影算子最早是在20世纪30年代由Murray和Lorch提出的，后来其他学者对其做了进一步研究，取得了丰硕的成果［4-13］.文献［7-8］研究了2个斜投影的乘积以及斜投影的分解，得出若干等价命题.文献［9］研究了加权广义逆、斜投影和最小二乘的若干问题.文献［10-11］在Hilbert空间的基础上，研究了Schur补和斜投影的相关性质.文献［12］基于C*代数系统研究了斜投影算子的性质.

本研究根据斜投影的定义、性质与空间直和分解，研究2个及3个斜投影乘积的性质，得到若干等价命题.

1　相关定义及引理

投影算子分为正交投影算子和斜投影算子，两者共同点是都具有幂等性.在一些文献中，为方便，常将斜投影算子看作矩阵，因此，斜投影算子也称为投影矩阵.设Pi为沿着空间Wi到空间Vi的投影，其中：.设R（Pi）为Pi的值域，N（Pi）为Pi的零空间，则R（Pi）=Vi，N（Pi）=Wi. Pi是投影矩阵，显然，Qi=I-Pi为沿着空间Vi到空间Wi的投影矩阵.

引理1设P1、P2为投影矩阵，则有

引理2［4］设P是从Cn到Cn的线性算子，则下列命题等价：

（1）P是Cn的投影算子；

引理3若P1P2=P2P1，则P1P（2或P2P1）为沿着W1+W2到V1∩V2的投影.

证明因为P1P2=P2P1，则有因此，P1P2是投影矩阵.设x∈V1∩V2，则有P（1P2x）=P1x=x.另一方面，设x∈W1+W2，x= x1+x2，其中：x1∈W1，x2∈W2.于是，P1P2x=P1P（2x1+ x2）=P1P2x1+P1P2x2=0.因此，En=（V1∩V2）⊕（W1⊕W2）.故P1P2是沿着W1+W2到V1∩V2的投影.

2　主要结果

定理1下列结论是等价的：

证明 （1）⇒（2）：将P2=I-Q2代入P1P2=P2P1，得P（1I-Q2）=（I-Q2）P1.因此P1Q2=Q2P1.注意到P2为沿着空间W2到空间V2的投影，而Q2为沿着空间V2到空间W2的投影，在等式中，将P2换成Q2，并交换V2和W2的位置，即得

（2）⇒（3）：将P1=I-Q1和Q2=I-P2代入P1Q2= Q2P1，得（I-Q1）（I-P2）=（I-P2）（I-Q1）.因此Q1P2= P2Q1.由于Pi为沿着空间Wi到空间Vi的投影，Qi为沿着空间Vi到空间Wi的投影矩阵.在等式中，将P1换成Q1，Q2换成P2，并交换Vi和 W（ii=1，2）的位置，即得

（3）⇒（4）：将P2=I-Q2代入Q1P2=P2Q1，得Q（1IQ2）=（I-Q2）Q1，即Q1Q2=Q2Q1.由于P2为沿着空间W2到空间V2的投影，在等式中，将P2换成Q2，并交换W2和V2的位置，即得

（4）⇒（1）：由Q1Q2=Q2Q1，得（I-P1）（I-P2）=（IP2）（I-P1），即P1P2=P2P1.由于Pi为沿着空间Wi到空间Vi的投影，在等式中，将Qi换成Pi，并交换Wi和Vi的位置，即得

推论1在定理1的条件下，有

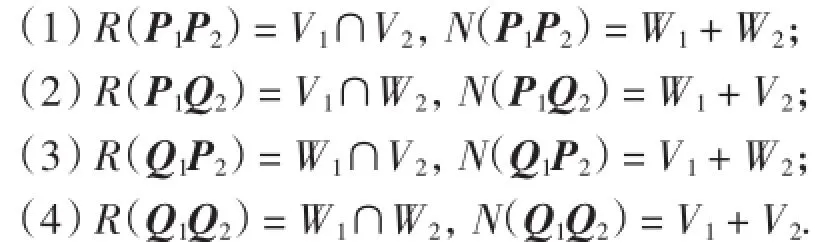
证明仅证明（1），其余结论证明方法相同.由于投影Pi为沿着零空间Wi到值域空间Vi的投影.故投影P1P2是沿着零空间W1+W2到值域空间V1∩V2的投影.因此R（P1P2）=V1∩V2，N（P1P2）=W1+W2.

推论2下列结论是等价的：

（1）P1+Q2为沿着空间W1∩V2到空间V1⊕W2的投影.

（2）P2-P1为沿着空间V1⊕W2到空间W1∩V2的投影.

此时，V1⊂V2，W2⊂W1.

证明 （1）⇒（2）：因为P1+Q2为沿着W1∩V2到V1⊕W2的投影，所以P1Q2=Q2P1=0.由定理1得，P1Q2=Q2P1⇔Q1P2=P2Q1.于是Q1P2=P2Q1=（I-Q2）（IP1）=I-P1-Q2.又由定理1可知，P2Q1为沿着V1⊕W2到W1∩V2的投影.而P1+Q2=I-P2Q1.因此P2-P1=I-（P1+Q2）为沿着V1⊕W2到W1∩V2的投影.

（2）⇒（1）：因为P2-P1为沿着V1⊕W2到W1∩V2的投影，所以P1P2=P2P1=P1.由此得P（1I-Q2）=（IQ2）P1=P1，即P1Q2=Q2P1=0.类似于（1）⇒（2）的证明，由定理1得P1Q2=Q2P1⇔Q1P2=P2Q1，Q1P2=P2Q1= I-P1-Q2，P2Q1为沿着V1⊕W2到W1∩V2的投影.因此，P1+Q2=I-P2Q1为沿着W1∩V2到V1⊕W2的投影.

对于（1），因为P1Q2=Q2P1=0，由P1Q2=0得R（Q2）⊂N（P1），即W2⊂W1.由Q2P1=0得R（P1）⊂N（Q2），即V1⊂V2.

对于（2），由P1P2=P1⇒P（1I-P2）=0⇒R（I-P2）⊂N（P1）⇒N（P2）⊂N（P1），得W2⊂W1.由P2P1=P1⇒（IP2）P1=0⇒R（P1）⊂N（I-P2）⇒R（P1）⊂R（P2），得V1⊂V2.

类似推论2，可得推论3～推论5.

推论3下列结论是等价的：

（1）P1+P2为沿着空间W1∩W2到空间V1⊕V2的投影.

（2）Q2-P1为沿着空间V1⊕V2到空间W1∩W2的投影.

此时，V1⊂W2，V2⊂W1.

推论4下列结论是等价的：

（1）Q1+Q2为沿着空间V1∩V2到空间W1⊕W2的投影.

（2）P2-Q1为沿着空间W1⊕W2到空间V1∩V2的投影.

此时，W2⊂V1，W1⊂V2.

推论5下列结论是等价的：

（1）Q1+P2为沿着空间V1∩W2到空间W1⊕V2的投影.

（2）Q2-Q1为沿着空间W1⊕V2到空间V1∩W2的投影.

此时，W1⊂W2，V2⊂V1.

定理2在定理1的条件下，下列结论是等价的：

证明仅证P1P2=P2P1的情形.其他3种情形类似可证.

（1）⇒（2）：由（P1P2）2=P1P2知P1P2P1P2=P1P2.将P2=I-Q2代入上式，得P1（I-Q2）P1（I-Q2）=P1（IQ2），即 P1Q2P1Q2=P1Q2P1.由定理 1的（2），得P1Q2P1Q2=Q2P21.注意到P21=P1，Q2P1=P1Q2.因此（P1Q2）2=P1Q2.

（2）⇒（3）：由（P1Q2）2=P1Q2知P1Q2P1Q2=P1Q2.注意到Q2=I-P2，P1=I-Q1，于是（I-Q1）（I-P2）（IQ1）（I-P2）=（I-Q1）（I-P2）.化简得Q1P2Q1P2= Q21P2.注意到Q21=Q1.因此（Q1P2）2=Q1P2.

（3）⇒（4）：由（Q1P2）2=Q1P2知Q1P2Q1P2=Q1P2.注意到P2=I-Q2，于是Q1（I-Q2）Q1（I-Q2）=Q1（IQ2）.化简得Q1Q2Q1Q2=Q1Q2Q1.由定理1的（4），得（Q1Q2）2=Q1Q2.

（4）⇒（1）：由（Q1Q2）2=Q1Q2知Q1Q2Q1Q2=Q1Q2.注意到Q1=I-P1，Q2=I-P2，于是（I-P1）（I-P2）（IP1）（I-P2）=（I-P1）（I-P2）.化简得P1P2P1P2= P1P2P1.由题设有P1P2=P2P1及P21=P1，可得（P1P2）2= P1P2.

定理3设En=V1⊕W1=V2⊕W2=V3⊕W3，则下列结论是等价的：

（1）若P1P2=P2P1，P1P3=P3P1，P2P3=P3P2，则P1P2P3为沿着W1+W2+W3到V1∩V2∩V3的投影.

（2）若P1P2=P2P1，P1Q3=Q3P1，P2Q3=Q3P2，则P1P2Q3为沿着W1+W2+V3到V1∩V2∩W3的投影.

（3）若P1Q2=Q2P1，P1Q3=Q3P1，Q2Q3=Q3Q2，则P1Q2Q3为沿着W1+V2+V3到V1∩W2∩W3的投影.

（4）若Q1Q2=Q2Q1，Q1Q3=Q3Q1，Q2Q3=Q3Q2，则Q1Q2Q3为沿着V1+V2+V3到W1∩W2∩W3的投影.

证明证法类似于引理3.

定理4若PiPj=PjPi=0，i，j=1，2，3，则P1+ P2+P3为沿着W1∩W2∩W3到V1⊕V2⊕V3的投影.此时，V2、V3⊂W1；V1、V3⊂W2；V1、V2⊂W3.

证明对任意x∈（V1⊕V2⊕V3），有分解x=x1+ x2+x3，其中：xi∈Vi（i=1，2，3）.注意到P1x2=P1P2x= 0，同理可得P1x3=0，P2x1=0，P2x3=0，P3x1=0，P3x2= 0.于是（P1+P2+P3）x=（P1+P2+P3）（x1+x2+x3）= P1x1+P2x2+P3x3=x1+x2+x3=x.由PiPj=PjPi=0，显然有P1=P1（I-P2-P3），P2=P2（I-P1-P3），P3= P3（I-P1-P2）.对任意x∈（W1∩W2∩W3），有（P1+ P2+P3）x=P1（I-P2-P3）x+P2（I-P1-P3）x+P3（IP1-P2）x=0.于是R（P1+P2+P3）=V1⊕V2⊕V3，N（P1+P2+P3）=W1∩W2∩W3.因此P1+P2+P3为沿着W1∩W2∩W3到V1⊕V2⊕V3的投影.

由P1P2=0⇒R（P2）⊂N（P1），即得V2⊂W1.由P2P1= 0⇒R（P1）⊂N（P2），即得V1⊂W2.同理，P1P3=0⇒V3⊂W1；P3P1=0⇒V1⊂W3；P2P3=0⇒V3⊂W2；P3P2=0⇒V2⊂W3.因此有V2、V3⊂W1，V1、V3⊂W2，V1、V2⊂W3.

类似定理4可得推论6.

推论6（1）若PiPj=PjPi=0，i，j=1，2，PiQ3= Q3Pi=0，则P1+P2+Q3为沿着W1∩W2∩V3到V1⊕V2⊕W3的投影.此时，V2、W3⊂W1，V1、W3⊂W2，V1、V2⊂V3.

（2）若QiQj=QjQi=0，i，j=2，3，P1Qi=QiP1=0，则P1+Q2+Q3为沿着W1∩V2∩V3到V1⊕W2⊕W3的投影.此时，V1、W3⊂W2，V2、W2⊂V3，W2⊂W1，W3⊂V2.

（3）若QiQj=QjQi=0，i，j=1，2，3，则Q1+Q2+Q3为沿着V1∩V2∩V3到W1⊕W2⊕W3的投影.此时，W2、W3⊂V1，W1、W3⊂V2，W1、W2⊂V3.

定理5在定理3的条件下，下列结论是等价的：

证明证法类似于定理2.

设Pk为沿着空间Wk到空间Vk的投影，根据斜投影的定义，Qk为沿着空间Vk到空间Wk的投影.

推论7设En=Vi⊕Wi，i=1，2，…，k，k≤n，则下列结论是等价的：

（1）若PiPj=PjPi，则P1P2…Pk为沿着W1+W2+ …+Wk到V1∩V2∩…∩Vk的投影.

（2）若PiPj=PjPi，PiQk=QkPi，则P1P2…Pk-1Qk为沿着W1+W2+…+Wk-1+Vk到V1∩V2∩…∩Vk-1∩Wk的投影.

（3）若P1Qj=QjP1，QiQj=QjQi，则P1Q2…Qk为沿着W1+V2+…+Vk到V1∩W2∩…∩Wk的投影.

（4）若QiQj=QjQi，则Q1Q2…Qk为沿着V1+V2+ …+Vk到W1∩W2∩…∩Wk的投影.

推论8设En=Vi⊕Wi，i=1，2，…，k，k≤n，且PiPj=PjPi=0，i，j=1，2，…，k，则P1+P2+…+Pk为沿着W1∩W2∩…∩Wk到V1⊕V2⊕…⊕Vk的投影.

定理6在推论7的条件下，下列结论是等价的：

参考文献：

［1］张钦宇，曹斌，王健，等.基于斜投影的极化滤波技术［J］.中国科学：信息科学，2010，40（1）：91-101. ZHANG Q Y，CAO B，WANG J，et al.Polarization filtering based on oblique projection［J］.Science China：Information Sciences，2010，40 （1）：91-101（in Chinese）.

［2］姚志英，曹海青.一种基于投影算子的二值图像处理算法［J］.计算机系统应用，2013，22（1）：95-98. YAO Z Y，CAO H Q.Binary image processing algorithm based on projection operator［J］.Computer Systems Applications，2013，22（1）：95-98（in Chinese）.

［3］田鹏武，康荣宗，于宏毅.基于斜投影算子的压缩域滤波法［J］.北京邮电大学学报，2012，35（3）：108-111. TIAN P W，KANG R Z，YU H Y.A compressive-domain filtering method based on oblique projector［J］.Journal of Beijing University of Posts and Telecommunications，2012，35（3）：108-111（in Chinese）.

［4］陈永林.广义逆矩阵的理论与方法［M］.南京：南京师范大学出版社，2005. CHEN Y L.Theory and Method of Generalized Inverse Matrix［M］.Nanjing：Nanjing Normal University Press，2005（in Chinese）.

［5］何旭初，孙文瑜.广义逆矩阵引论［M］.南京：江苏科学技术出版社，1990. HE X C，SUN W Y.Introduction of Generalized Inverse Matrix［M］. Nanjing：Jiangsu Science and Technology Press，1990（in Chinese）.

［6］RAO C R，MITRA S K.Generalized Inverses of Matrices and Its Applications［M］.New York：Wiley，1971.

［7］TAKANE Y，YANAI H.On oblique projectors［J］.Linear Algebra Appl，1999（289）：297-310.

［8］GROB J，TRENKLER G.On the product of oblique projectors［J］.Linear Multilinear Algebra，1998（44）：247-259.

［9］CORACHG，MAESTRIPIERIA.Weightedgeneralizedinverses，oblique projections and least squares problems［J］.Numer Funct Anal Optim，2005，26（6）：659-673.

［10］CORACH G，MAESTRIPIERI A，STOJANOFF D.Schur complements and oblique projections［J］.Acta Sci Math，2001，67：439-459.

［11］CORACH G，MAESTRIPIERI A，STOJANOFF D.Generalized Schur complements and oblique projections［J］.Linear Algebra and Appl，2002，341：259-272.

［12］ANDRUCHOW E，CORACH G，STOJANOFF D.Geometry of oblique projections［J］.Studia Math，1999，137：61-79.

［13］BEN-ISRAEL A，GREVILLE T N E.Generalized Inverses：Theory and Applications［M］.2nd ed.New York：Springer，2003.

（责任编校马新光）

第一作者：周玉兴（1973—），男，讲师.主要从事数值代数和矩阵分析方面的研究．

文章编号：1671-1114（2016）01-0012-02

中图分类号：O153.3

文献标志码：A

收稿日期：2015-01-25

基金项目：国家自然科学基金资助项目（11161004）；广西自然科学基金资助项目（2013GXNSFAA019008）.

Some properties of oblique projection product

ZHOU Yuxing1，HUANG Jingpin2，LIU Xiaoji2，TU Huonian3
（1.College of Shiyuan，Guangxi Teachers Education University，Nanning 530226，China；
2.College of Science，Guangxi University for Nationalities，Nanning 530006，China；
3.College of Information and Statistics，Guangxi University of Finance and Economics，Nanning 530003，China）

Abstract：According to the definition and properties of oblique projection，and combining the space direct sum decomposition，the properties of a product of two oblique projection are studied，and some equivalent propositions are given.The similar results of product of three or multiple oblique projection are also given.

Keywords：product of oblique projection；direct sum decomposition；oblique projection operator；projection matrix