基于高斯隶属函数的非线性T-S模糊系统的逼近性

张国英，王贵君（天津师范大学 数学科学学院，天津 300387）

基于高斯隶属函数的非线性T-S模糊系统的逼近性

张国英，王贵君
（天津师范大学 数学科学学院，天津 300387）

摘要：基于最小推理机、单点模糊化和中心平均解模糊化方法构造了一类非线性T-S模糊系统，根据Stone-Weierstrass定理证明了该T-S模糊系统对多元连续函数具有逼近性能.

关键词：最小推理机；高斯隶属函数；非线性T-S模糊系统；逼近性

模糊系统是基于知识或规则的系统，从数学的观点来看，它又是一种非线性映射，其系统内部主要是由一系列语言规则所构造，人们可通过选择不同隶属度函数得到诸多类型的模糊系统.文献［1-2］基于乘积推理机、单点化和中心平均解模糊化构造了T-S模糊系统，并详细研究了该系统的逼近性能.文献［3-6］对高维系统实施不同的低维分层来连接整个系统，从而不仅降低了系统内部的规则数，而且也能保持分层后的系统的逼近性能.文献［7］将多维输入变量进行增一型输入，从而得到多个子系统，最终形成一个与原模糊系统等价的递阶模糊系统，并证明了该系统的泛逼近性.文献［8］基于乘积推理机、单点模糊化和中心平均解模糊化构造了一种非线性T-S模糊系统，并证明了该系统对多元连续函数具有逼近性.文献［9-10］将各维变量两两输入到模糊系统中，以此方式形成了二叉树型模糊系统，并分别讨论了该系统的构造和模糊规则数的缩减问题，这些结果可有效地应用于模糊控制与系统建模.通常模糊系统都是采用乘积推理机、单点模糊化和中心平均解模糊化3个环节来构造的，该类系统对连续函数、可积函数的逼近性能也得到证明.本研究基于最小推理机、单点模糊化和中心平均解模糊化构造一种非线性T-S模糊系统，并利用Stone-Weierstrass定理详细证明该系统对连续函数具有逼近性能.

1　非线性T-S模糊系统

模糊系统是基于模糊IF-THEN规则库的非线性映射，其各部分均以合理方式执行这些规则.具体来说，在输入论域U⊂Rn上的模糊规则库由以下模糊规则形式组成：∀x=（x1，x2，…，xn）∈U，

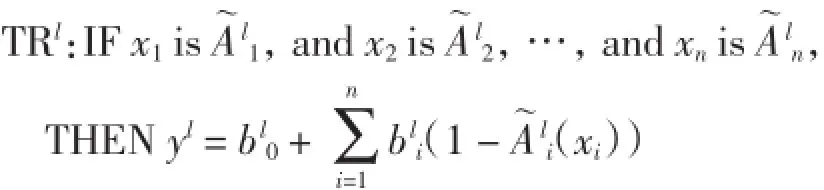
其中：l=1，2，…，m；m为系统规则总数.

从结构上看，一般模糊系统主要由模糊推理机、模糊化和解模糊化构成.常见的模糊推理机有乘积推理机、最小推理机、Lukasiewicz推理机、Zadeh推理机和Dienes-Rescher推理机.模糊化主要有单值模糊化、高斯模糊化和三角形模糊化.解模糊化主要有重心法解模糊化、中心平均解模糊化和最大值解模糊化.

基于最小推理机、单点模糊化和中心平均解模糊化给出模糊系统如下：

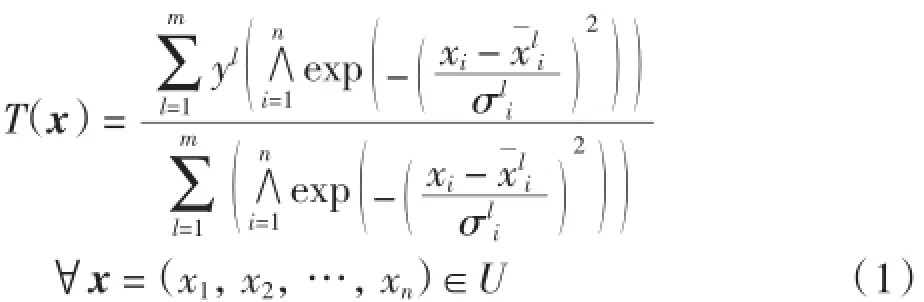
2　模糊系统的逼近性

带有单点模糊化、最小推理机和中心平均解模糊化的模糊系统是非线性函数的特殊类型，无论模糊系统是否用于控制器设计、决策分析或信号处理等功能，从函数逼近角度研究模糊系统都有重要意义.为此，下面利用Stone-Weierstrass定理证明系统（1）可按任意精度逼近紧集上的连续函数.

引理1［11］Stone-Weierstrass定理）令Z（U）为紧集U⊂Rn上的连续函数构成的集合，如果

（i）Z（U）是代数，即集合Z（U）对加法、乘法和标量积是封闭的；

（ii）Z（U）分离了U上的点，即∀x、y∈U，x≠y，存在T∈Z（U），使得T（x）≠T（y）；

（iii）Z（U）使得U中的点不为0，即∀x∈U，存在T∈Z（U），使得T（x）≠0.

则∀ε＞0，∀f∈Z（U），必存在T∈Z（U），使得

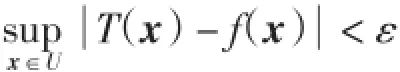
引理2∀ai、bj∈R+，i，j=1，2，…，n，有

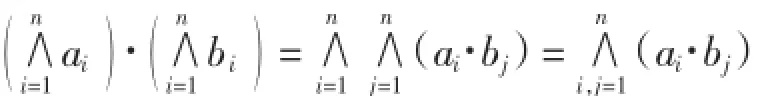
定理设紧集U⊂Rn，f是U上任一连续函数，则∀ε＞0，必存在形如式（1）的非线性T-S模糊系统T，使得∀x=（x1，x2，…，xn）∈U，有

证明为方便，令

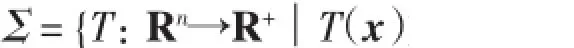
（i）首先，由式（1），∀T1、T2∈Σ，∀x=（x1，x2，…，xn）∈U，设

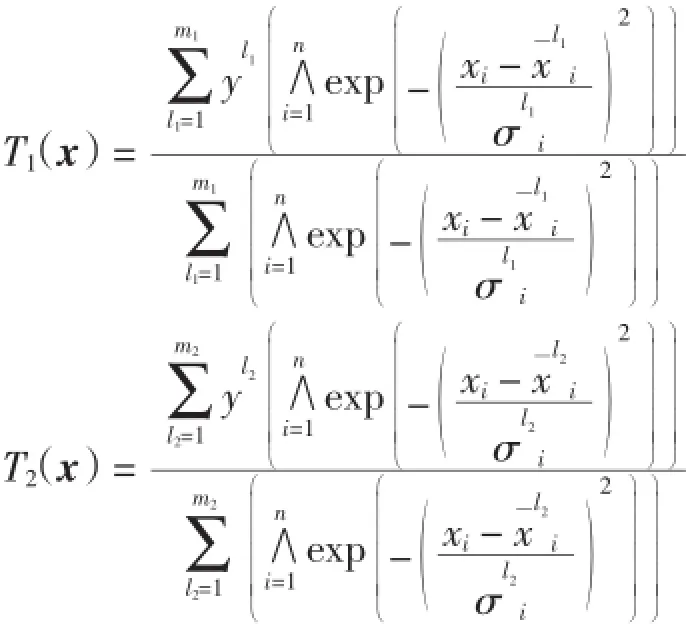
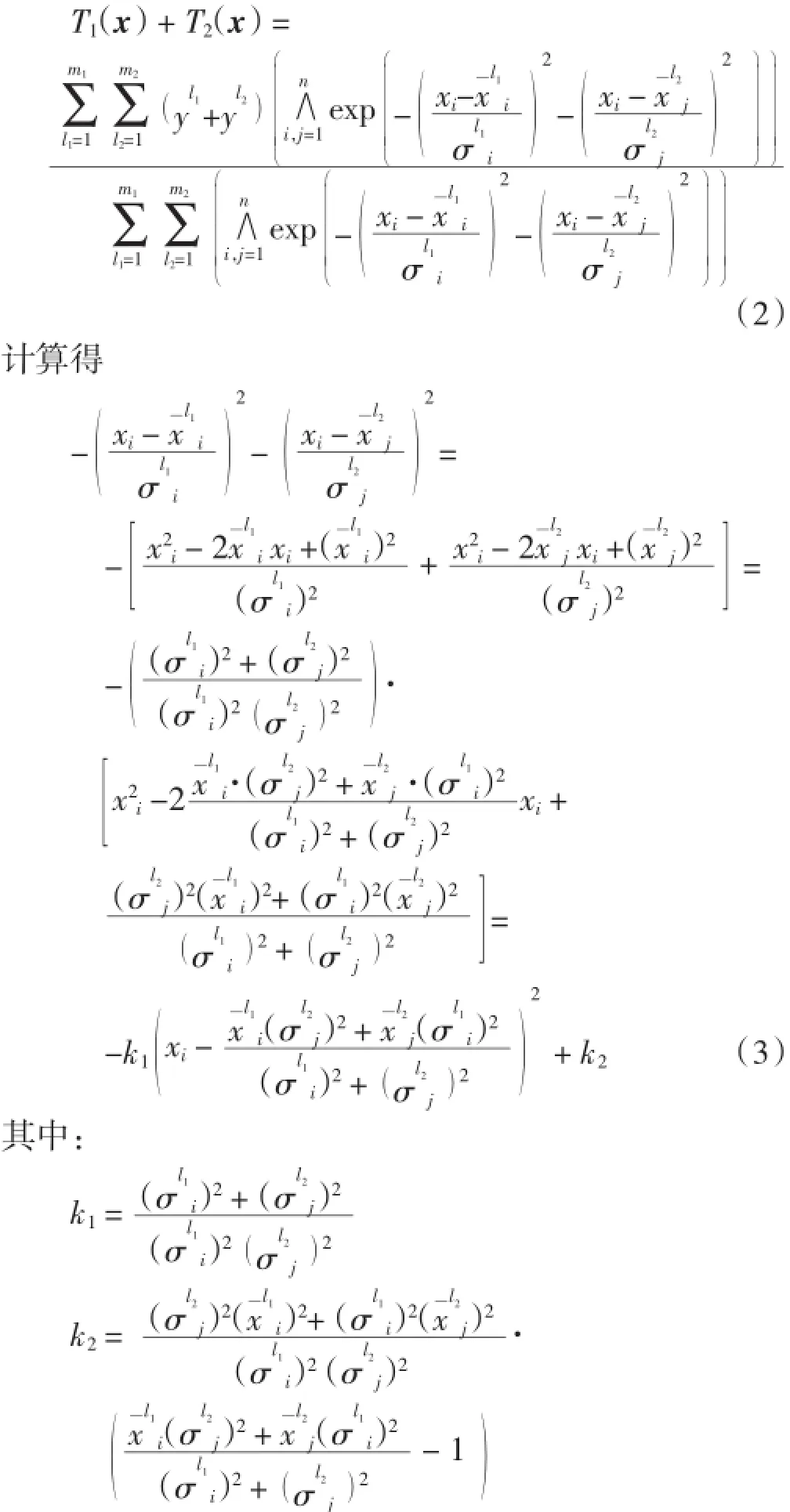
这里k1和k2对输入变量x（i分量）来说可视为非负常数.因此有

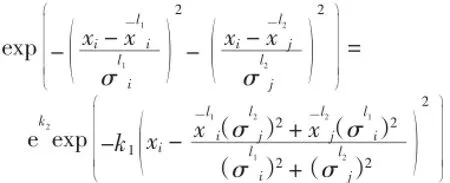
其次，∀x=（x1，x2，…，xn）∈U，由引理2，T（1x）· T（2x）可表示为

最后，∀c∈R+，∀x=（x1，x2，…，xn）∈U，显然有

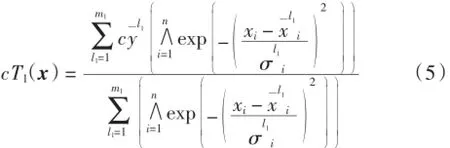
取中心点yl=cyl1，则式（5）即为式（1）的形式，故cT1∈Σ.

由上述证明知算子空间Σ对加法、乘法和标量积运算是封闭的，故空间Σ构成代数.

（ii）根据引理1，若使空间Σ分离U上的点，只需构造一个特殊的模糊系统T0，使得不同输入变量在模糊系统T0作用下的函数取值不同即可.为此，在紧集U上取定两点和，且x0≠z0.

显然，当x0≠z0时，必有T（x0）≠T（z0），故Σ可分离U上点.

（iii）由非线性T-S模糊系统的表达式（1）可知，∀x∈U，T（x）＞0，故Σ使得U上任一点的函数值均非零.

综上，根据Stone-Weierstrass定理，对紧集U上任意实值连续函数f和任意ε＞0，必存在形如式（1）的模糊系统T，使得对任意的x=（x1，x2，…，xn）∈U，T可按任意精度逼近连续函数f，即有

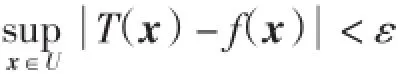
参考文献：

［1］LIU P Y，LI H X.Approximation of generalized fuzzy systems to integrable functions［J］.ScienceinChina：SeriesE，2000，30（5）：413-423.

［2］LIU P Y，LI H X.Analyses for L（pμ）-norm approximation capability of the generalized Mamdani fuzzy systems［J］.Information Sciences，2001，138（2）：195-210.

［3］ WANG L X.Universal approximator by hierarchical fuzzy systems［J］. Fuzzy Sets and Systems，1998，93（2）：223-230.

［4］WANG L X.Analysis and design of hierarchical fuzzy systems［J］.IEEE Trans on Fuzzy Systems，1999，7（5）：617-624.

［5］孙多青，霍伟.基于分层模糊系统的直接自适应控制［J］.控制与决策，2002，17（4）：465-468. SUN D Q，HUO W.Direct adaptive control based on hierarchical fuzzy systems［J］.Control and Decision，2002，17（4）：465-468（in Chinese）.

［6］孙多青，霍伟.具有任意形状隶属函数的分层模糊系统逼近性能研究［J］.控制理论与应用，2003，20（3）：377-381. SUN D Q，HUO W.Study on universal approximation of hierarchical fuzzy systems with arbitrary membership functions［J］.Control Theory and Applications，2003，20（3）：377-381（in Chinese）.

［7］张宇卓，李洪兴.广义递阶Mamdani模糊系统及其泛逼近性［J］.控制理论与应用，2006，23（3）：449-454. ZHANG Y Z，LI H X.Generalized hierarchical Mamdani fuzzy systems and their universal approximation［J］.Control Theory and Applications，2006，23（3）：449-454（in Chinese）.

［8］刘福才，马丽叶，邵静，等.一类非线性T-S模糊系统的通用逼近性［J］.自动化与仪器仪表，2007，129（1）：8-15. LIU F C，MA L Y，SHAO J，et al.Universal approximation of a kind of nonlinear T-S fuzzy system［J］.Automation and Instrumentation，2007，129（1）：8-15（in Chinese）.

［9］杨阳，王贵君，杨永强.基于二叉树型分层的广义混合模糊系统推理规则数的缩减［J］.控制理论与应用，2013，30（6）：765-772. YANG Y，WANG G J，YANG Y Q.Reducing the number of inference rules for generalized hybrid fuzzy systems based on binary tree-type hierarchy［J］.Control Theory and Applications，2013，30（6）：765-772（in Chinese）.

［10］杨阳，杨永强，王贵君.二叉树型分层广义混合模糊系统的结构和规则数分析［J］.天津师范大学学报：自然科学版，2014，34（1）：11-15. YANG Y，YANG Y Q，WANG G J.Analysis of structure and rule numbers for binary tree-type hierarchy generalized hybrid fuzzy systems［J］. Journal of Tianjin Normal University：Natural Science Edition，2014，34 （1）：11-15（in Chinese）.

［11］RUDIN W.Principles of Mathematical Analysis［M］.New York：Mc-Graw-Hill，1976.

［12］王立新.模糊系统与模糊控制教程［M］.北京：清华大学出版社，2003. WANG L X.A Course in Fuzzy Systems and Control［M］.Beijing：Tsinghua University Press，2003（in Chinese）.

（责任编校马新光）

第一作者：张国英（1991—），女，硕士研究生.

中图分类号：O159；TP183

文献标志码：A

收稿日期：2015-02-23

基金项目：国家自然科学基金资助项目（61374009）.

通信作者：王贵君（1962—），男，教授，主要从事模糊神经网络、模糊系统分析、模糊测度与积分方面的研究.

Approximation of nonlinear T-S fuzzy system based on Gaussian membership function

ZHANG Guoying，WANG Guijun
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

Abstract：A new class of nonlinear T-S fuzzy system is established based on the minimum inference engine，Gaussian membership function and the center average defuzzifier.The approximation performance of nonlinear T-S fuzzy system to a multivariate continuous function is proved according to the Stone-Weierstrass theorem.

Keywords：minimum inference engine；Gaussian membership function；nonlinear T-S fuzzy system；approximation