基于MATLAB的现代控制理论实验教学实践
2016-09-06何德峰徐建明
何德峰, 俞 立, 徐建明
(浙江工业大学 信息工程学院, 浙江 杭州 310023)
基于MATLAB的现代控制理论实验教学实践
何德峰, 俞立, 徐建明
(浙江工业大学 信息工程学院, 浙江 杭州310023)
针对现代控制理论的课程特点,进行了基于MATLAB语言的现代控制理论仿真实验教学研究。根据课程教学内容,给出了现代控制理论课程中6个教学仿真实验的实验目的、实验原理和实验步骤,并以“利用MATLAB求解极点配置问题”实验为例说明实验过程。教学实践表明,仿真实验有助于学生理解课程的理论知识、提高学习效率和学习积极性。
控制理论实验; 仿真实验; 实验教学; MATLAB
现代控制理论是大学自动化类专业的专业基础课,在自动化类专业本科教学中占有十分重要的地位。但现代控制理论的教学内容包含大量的矩阵运算和复杂的公式证明[1-2],内容抽象且理论性很强,学生不易理解。对此,有必要通过引入实验课的教学,帮助学生理解和掌握现代控制理论知识。基于MATLAB开发现代控制理论仿真实验,不但可以解决硬件实验设备不足的困难[3-5],而且可以供学生在课后进行自主性和探索性学习。
MATLAB是一款高性能数值运算软件,也是适合多学科、功能强大的系统仿真软件[6]。由于现代控制理论的主要数学工具是线性代数和常微分方程理论,而MATLAB以矩阵为基本运算单元,同时又可以调用预先定义的函数求解不同类型的控制问题,具有良好的交互分析功能。因此,MATLAB语言为现代控制理论课程的实验教学提供了一种很好的教学工具[7-9]。针对现代控制理论课程的教学内容,笔者给出6个基于MATLAB的现代控制理论教学仿真实验设计,包括实验目的、实验原理和实验步骤。
1 现代控制理论MATLAB仿真实验
现代控制理论主要讲授控制系统的状态空间模型、运动分析、能控性与能观性分析、李雅普诺夫稳定性理论、状态反馈控制器和状态观测器设计,以及线性最优控制等教学内容[1-2]。笔者针对这些教学内容并结合MATLAB的功能,设计了6个教学仿真实验。这些实验所需的实验设备仅包括1台中高档PC机(CPU 1.8 GHz以上、内存 1 GB以上、显卡 512 MB以上)、Windows操作系统和MATLAB 6.0以上版本。
1.1基于MATLAB的传递函数和状态空间模型的转换
(1) 实验目的。学习系统状态空间模型的建立方法;通过编程、上机调试,掌握系统状态空间模型与传递函数相互转换的方法。
(2) 实验原理简述。控制系统的状态空间模型为
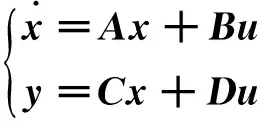
(1)
(2)
式中I为单位矩阵。
表示系统(1)的状态空间模型和传递函数的MATLAB函数分别为ss(A,B,C,D)和tf(num,den),其中num表示传递函数G(s)中分子多项式的系数向量(单输入单输出系统);den表示传递函数G(s)中分母多项式的系数向量。状态空间模型和传递函数相互转换的MATLAB函数分别为
[A,B,C,D]=tf2ss(num,den),
[num,den]=ss2tf(A,B,C,D,ui)
其中,对多输入系统,必须确定ui(ui为控制向量的第i个元素)的值。该函数的结果是第ui个输入到所有输出的传递函数。
(3) 实验步骤。根据系统(1)的传递函数G(s)或状态空间模型(A,B,C,D),对应转换式(2),采用MATLAB相关函数编写m文件;在MATLAB界面下调试程序。
1.2基于MATLAB的状态空间模型进行分析
(1) 实验目的。根据状态空间模型,分析系统由初始状态和外部激励所引起的响应;通过编程、上机调试,掌握系统运动的分析方法。
(2) 实验原理简述。在控制系统(1)的状态空间模型中,设系统的初始时刻为0,初始状态为x(0),则系统的状态响应x(t)和输出响应y(t)分别为:
(3)
(4)
状态响应由系统自由运动(即初始状态响应)和由控制输入引起的运动组成;输出响应由初始状态引起的零输入响应、外部输入响应和系统输入的直接传输部分组成。系统响应分析的MATLAB函数命令包括:initial(A,B,C,D,x0)可以得到系统输出对初始状态x0的时间响应;step(A,B,C,D)给出了系统的单位阶跃响应曲线;impulse(A,B,C,D)给出了系统的单位脉冲响应曲线;[y,T,x]=lsim(sys,u,t,x0) 给出状态空间模型对任意输入的响应,其中sys表示贮存在计算机内的状态空间模型,它可以由函数sys=ss(A,B,C,D)产生。
(3) 实验步骤。构建系统的状态空间模型,采用MATLAB的m文件编程;求取系统的状态和输出响应;在MATLAB界面下调试程序,并检查运行是否正确。
1.3基于MATLAB的连续时间状态空间模型的离散化
(1) 实验目的。导出系统的连续时间状态空间模型相应的离散化状态空间模型;通过编程、上机调试,掌握离散系统运动分析方法。
(2) 实验原理简述。考虑控制系统(1)的状态空间模型和输入信号的采样保持性
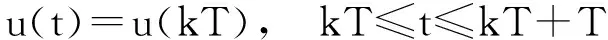
(5)
其中,T表示系统的采样周期。则连续时间控制系统(1)的状态空间模型离散化方程可以写成:
(6)
上述离散化过程的MATLAB函数为[G, H]=c2d(A, B, T)。
(3) 实验步骤。导出连续状态空间模型的离散化模型,采用MATLAB相关函数编写m文件;在MATLAB界面下调试程序,并检查是否运行正确。
1.4利用MATLAB求解极点配置问题
(1) 实验目的。通过编程、调试,掌握极点配置状态反馈控制器设计方法。
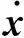
MATLAB软件提供了两个函数acker和place来确定极点配置状态反馈控制器的增益矩阵K。函数acker是基于求解极点配置问题的爱克曼公式,它只能应用到单输入系统,要配置的闭环极点中可以包括多重极点。用函数acker和place表示K的一般形式,K=acker(A,B,J)和K=place(A,B,J),其中的J=[λ1,λ2, …,λn]表示n个期望闭环极点。得到增益K后,可以用命令eig(A-BK)检验闭环极点。
(3) 实验步骤。根据系统(1)的状态空间模型(A,B,C,D)和n个期望闭环极点,采用MATLAB相关函数编写m文件;在MATLAB界面下调试程序,并检查是否运行正确。
1.5利用MATLAB设计状态观测器
(1) 实验目的。学习状态观测器设计原理和算法;通过编程、上机调试,理解观测器极点对观测器性能的影响;掌握基于MATLAB语言的状态观测器设计方法。
(2) 实验原理简述。根据控制系统(1)的状态空间模型,设计龙伯格全阶状态观测器:
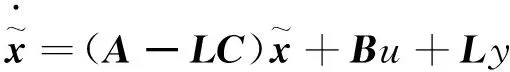
(7)

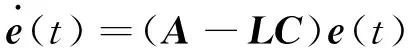
(8)
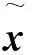
关于系统(1)的降阶观测器设计如下。假定系统(1)的矩阵C具有形式[1 0](对一般结构的矩阵,需要作适当的变换),根据矩阵C的结构,将系统状态分成可直接测量状态变量xa和不可直接测量状态变量xb两部分。据此,将系统(1)状态空间模型中的矩阵和作相应的分块,则该状态空间模型可以写成
(9)
其中,xb是要估计的状态变量。设计降阶观测器
(10)

(3) 实验步骤。根据系统(1)的状态空间模型(A,B,C,D)和观测器给的期望闭环极点,采用MATLAB相关函数编写m文件;在MATLAB界面下调试程序,并检查是否运行正确。
1.6利用MATLAB设计线性二次型最优控制器
(1) 实验目的。学习线性二次型最优控制理论;通过编程、上机调试,掌握线性二次型最优控制器设计方法。
(2) 实验原理简述。考虑控制系统(1)的状态空间模型,给定性能指标:
(11)
其中,Q为对称正定(或半正定)矩阵,R为对称正定矩阵。性能指标(11)右边的第一项表示对状态的要求,第二项是对输入能量的限制。考虑状态反馈控制器,使得性能指标(11)最小化的最优控制器为u=-Kx,其中K=R-1B′P是mxn维状态反馈增益矩阵,P是黎卡提矩阵方程(12)的对称正定解矩阵。
PA+A′P-PBR-1B′P+Q=0
(12)
(3) 实验步骤。根据系统(1)的状态空间模型和性能指标(11),采用MATLAB相关函数编写m文件;在MATLAB界面下调试程序,并检查设计结果的正确性。
2 实验教学实践
以极点配置状态反馈控制器设计为例,详细说明实验“利用MATLAB求解极点配置问题”的实验教学过程。
考虑一个控制系统为

(13)
设计一个状态反馈控制器u=-Kx,使得闭环系统的极点为{-2+j4,-2-j4,-10},进而对给定初始状态x(0)=[1 0 0]'测试闭环系统的状态响应。
执行以下应用函数acker编制的m文件:
A=[0 1 0; 0 0 1; -1 -5 -6];B=[0;0;1];
得到K=[199 55 9]。
若执行以下应用函数place编制的m文件:
A=[0 1 0; 0 0 1; -1 -5 -6];B=[0;0;1];
K=place(A,B,);
得到K=[199 55 9]。
对给定初始状态,应用MATLAB函数initial测试闭环系统的状态响应,编制m文件:
sys=ss(A-B*K,[0;0;0],eye(3),0);
t=0:0.01:4;
x=initial(sys,[1;0;0],t);
x1=[1 0 0]*x’;
x2=[0 1 0]*x’;
x3=[0 0 1]*x’;
subplot(3,1,1);
plot(t,x1), grid;
title(‘Response to Initial Condition’);
ylabel(‘x1’);
subplot(3,1,2);
plot(t,x2), grid;
ylabel(‘x2’);
subplot(3,1,3);
plot(t,x3), grid;
xlabel(‘t (sec)’);
ylabel(‘x3’);
可得闭环系统的状态响应曲线如图1所示。
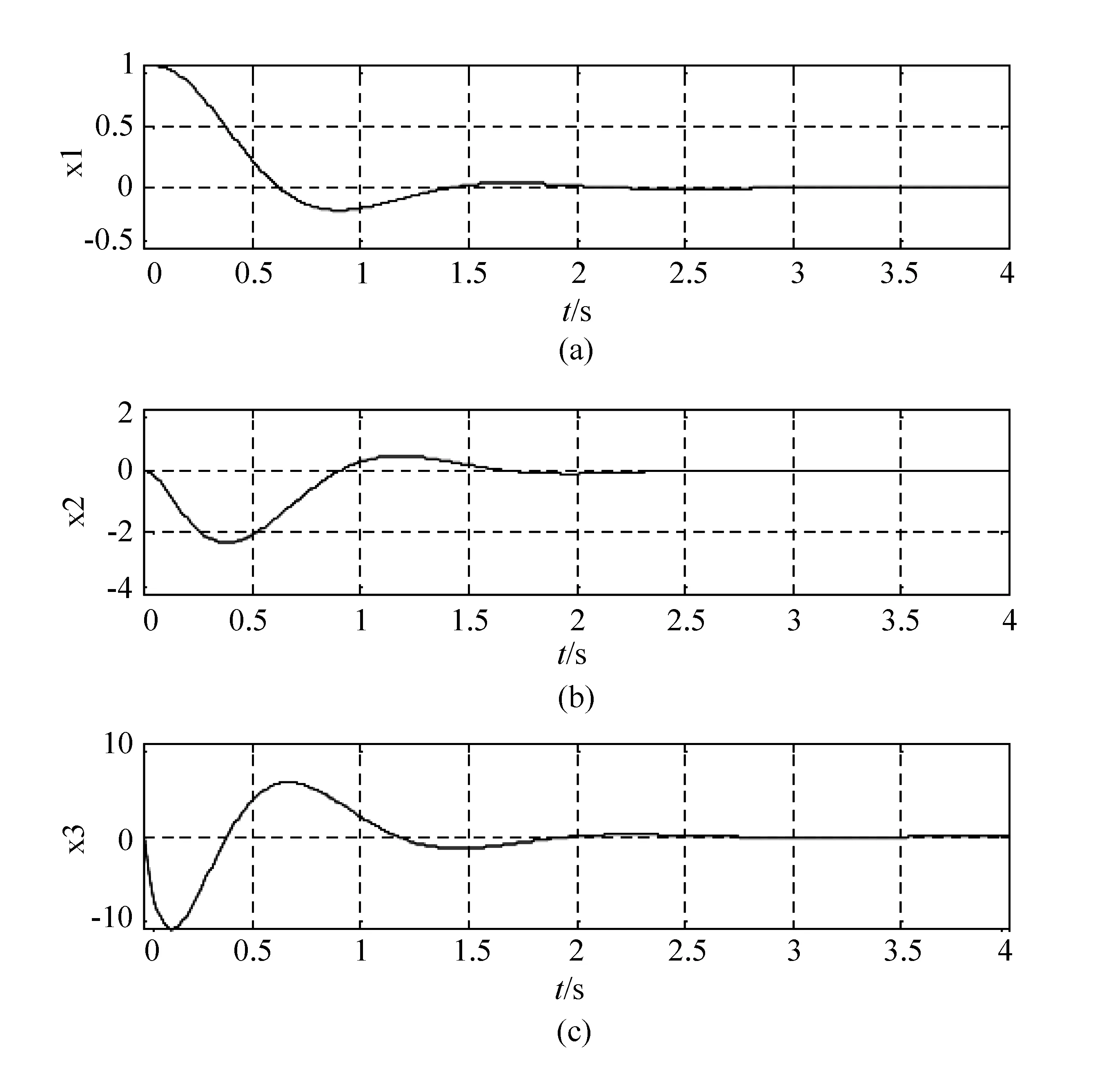
图1 初始状态响应图
在实验过程中,教师现场编程演示与实时指导,然后学生应用MATLAB函数acker和place编写m文件,执行m文件得到被控系统的状态反馈控制器,使得闭环系统的极点配置到预先给定的位置。进一步,为检验所设计的状态反馈控制器的控制性能,应用initial函数编写m文件,测试闭环系统的状态响应。如果状态响应不理想,如振荡频繁、超调量大等,那么就要求学生移动期望闭环极点,然后再重复整个设计过程,直到闭环系统得到满意的状态响应。这样就可以利用MATLAB对状态响应曲线进行直观显示,让学生理解基于极点配置的状态反馈控制器设计的原理、过程和方法。
教学实践表明,通过MATLAB实验,学生可以把课堂教学中学到的基本原理和基础性知识与实际系统的控制相结合,不仅加深了对书本知识的理解,更重要的是培养了学生的实际工作能力。
3 结语
笔者将MATLAB引入现代控制理论课程的实验教学中,所设计的6个仿真教学实验覆盖了该课程的主要教学内容。通过近3年的教学实践表明,基于MATLAB的仿真教学实验不仅有助于学生对现代控制理论课程抽象知识点的理解和掌握,还有助于提高学生的学习积极性和灵活运用课本知识的能力,同时对学生熟悉和应用MATLAB语言也有积极作用。
References)
[1] 俞立.现代控制理论[M].北京:清华大学出版社,2007.
[2] 张嗣瀛,高立群.现代控制理论[M].北京:清华大学出版社,2006.
[3] 叶彪明.基于MATLAB的《现代控制理论》课程的实验设计[J].实验室研究与探索,2004,23(1):28-30.
[4] 范秋凤,李正斌.基于MATLAB的现代控制理论课程教学改革[J].才智,2010(28):266-267.
[5] 刘强,贾鸿莉,董德发.Matlab在现代控制理论教学中的应用[J].现代电子技术,2010(18):71-72.
[6] Katsuhiko Ogata.控制理论MATLAB教程[M].英文版.北京:电子工业出版社,2008.
[7] 高立群,杨姝,韩杰,等.关于本科生教学改革的实践思考:以《现代控制理论》课为例[J].辽宁教育研究,2006(11):78-79.
[8] 黄忠霖.新编控制系统MATLAB仿真实训[M].北京:机械工业出版社,2013.
[9] 薛定宇.控制系统计算机辅助设计:MATLAB语言与应用 [M].2版.北京:清华大学出版社,2006.
Experimental teaching and practice of modern control theory based on MATLAB
He Defeng, Yu Li, Xu Jianming
(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)
The simulation experimental teaching of Modern Control Theory is studied based on MATLAB language for the characteristics of the Modern Control Theory course. According to the teaching content of the course, six simulation experiments for teaching are presented, including the experimental purpose, experimental principle, experimental procedure, etc. One of these experiments is used to illustrate the practice of teaching process. The teaching practice shows that these simulation experments are helpful for students to understand the theoretical knowledge of the course and to improve students’ learning efficiency and enthusiasm.
modern control theory; simulation experiment; experimential teaching; MATLAB
10.16791/j.cnki.sjg.2016.03.031
2015- 09- 21
《现代控制理论》国家精品资源共享课程建设项目(教高司函(2013)132号)
何德峰(1979—),男,浙江义乌,博士,教授,从事现代控制理论与应用教学研究.
E-mail:hdfzj@zjut.edu.cn,lyu@zjut.edu.cn
TP273.1
A
1002-4956(2016)3- 0123- 04
