脉冲噪声的非线性变换有源控制算法研究

李　沛, 张景荣

(北京信息科技大学 机电实习中心, 北京　100192)



脉冲噪声的非线性变换有源控制算法研究

李沛, 张景荣

(北京信息科技大学 机电实习中心, 北京100192)

α稳定分布模型是描述脉冲噪声的最佳理论工具,研究了对称α稳定分布脉冲噪声的有源控制；对基于非线性变换的脉冲噪声有源控制算法进行了推导与分析,并对FXSigmod算法进行了计算机仿真,用实验证实算法消除噪声的效果。该算法无需估测阈值,容易实现,连续更新性能好,可快速有效抑制脉冲噪声。

脉冲噪声； 非线性变换； 有源控制；α稳定分布

噪声污染是新世纪要攻克的主要环境问题。医疗跟踪调查表明:噪声不仅仅会损伤听力,还会诱发多种致癌、致命的疾病。环境中出现的噪声,按噪声辐射能量随时间的变化可分为稳态噪声、非稳态噪声。 非稳态噪声对人体的伤害程度明显高于稳态噪声。具有显著尖峰特性的脉冲噪声(如锻造、爆炸、冲压、婴儿恒温箱等产生的噪声)的危害程度更加严重。医学检查提示:长期接触脉冲噪声的工人的中枢神经系统功能状态出现了改变,诱发了大脑皮层功能的变化,表现为以α波为主节律的正常的脑电波减少,而以β波为主节律的杂乱波形增多,诱发试验潜伏期、恢复期延长,同时尿检中可见尿中儿茶酚胺含量增高,危害很大[1],严重影响人们身体健康和生活。尤其是长期工作在高强度振动环境中的工人,会由于受噪声干扰而出现产品质量问题,甚至发生事故。由此可见,对脉冲噪声进行有效控制更为关键。

噪声控制一般分为两大类:被动和主动噪声控制。被动噪声控制是对声源、噪声传播途径及接受者方面进行控制和处理,如吸声、消声、隔声、隔阻尼等。主动噪声控制又称为有源噪声控制(active noise control,简称ANC)是从噪声源和振动源方面着手进行处理。通过系统控制喇叭的输出,主动去产生一个反相信号,这个信号与原有噪声信号幅值相同但相位相反,把两者进行叠加从而抵消掉噪声,达到降低噪声幅值、有效控制噪声的目的。

1　α稳定分布

具有显著尖峰特性的脉冲噪声随机信号,通常采用对称α稳定分布[2-3](symmetric α stable distribution,SαS)来建模。实践证明:α稳定分布模型是描述脉冲噪声的最佳理论工具,它与高斯分布的主要区别在于拖尾,α稳定分布的拖尾比高斯分布的拖尾要厚。与高斯分布具有指数拖尾不同,α稳定分布具有代数拖尾 。α稳定分布最早是在数学领域中被广泛使用,在信号处理领域中引起关注还仅仅是从1993年才开始。目前信号处理领域中热门研究的课题,是把α稳定分布作为理想数学模型来描述非高斯的脉冲噪声,在对α稳定分布研究中发现,存在一些具有较大幅值的随机样本,它们远离分布中心位置,而使得原来的基于最小均方误差准则的算法不再收敛的关键因素正是这些大幅值样本的干扰。脉冲噪声的尖峰、厚尾、无限二阶矩、重复性等特点决定了对它的有源控制还处于摸索研究阶段。

α稳定分布的特征指数属于非高斯分布,有无限二阶矩,但是经典ANC算法(最小均方算法FxLMS)均以最小均方误差(二阶矩)为准则。对于α稳定分布随机变量,分散系数γ表示α稳定分布的分散程度,和高斯分布里的方差的概念相类似。因此,脉冲噪声有源控制算法常会考虑下面的办法:一种是在α稳定分布中,以最小分散系数准则取代最小均方误差准则,也就是在设计有源噪声控制器时把残差信号的分散系数最小作为目标；另一种想法是因为SαS脉冲噪声具有无穷二阶矩,因此无法基于均方误差准则进行计算,由此想到可否对其进行一些变换,变换以后的过程具有有限二阶矩,然后再利用传统的基于均方误差准则等方法进行进一步处理,这样,充分继承了传统算法的优点,减少算法的计算量,又使得算法具有良好的收敛性[4-6]。

2　基于非线性变换脉冲噪声有源控制算法推导与分析

由于α稳定分布信号方差不存在,也就是说没有有限的二阶矩,由此设想,对其进行非线性变换,使变换后的过程具有有限二阶矩,再利用基于二阶矩的算法进行处理,工作量小并且算法成熟可靠,收敛速度快。分析表明:对数函数、S型函数、反正切函数等非线性函数都可以抑制尖峰脉冲特性的影响,具有有限方差。非线性预处理方法如图1所示。

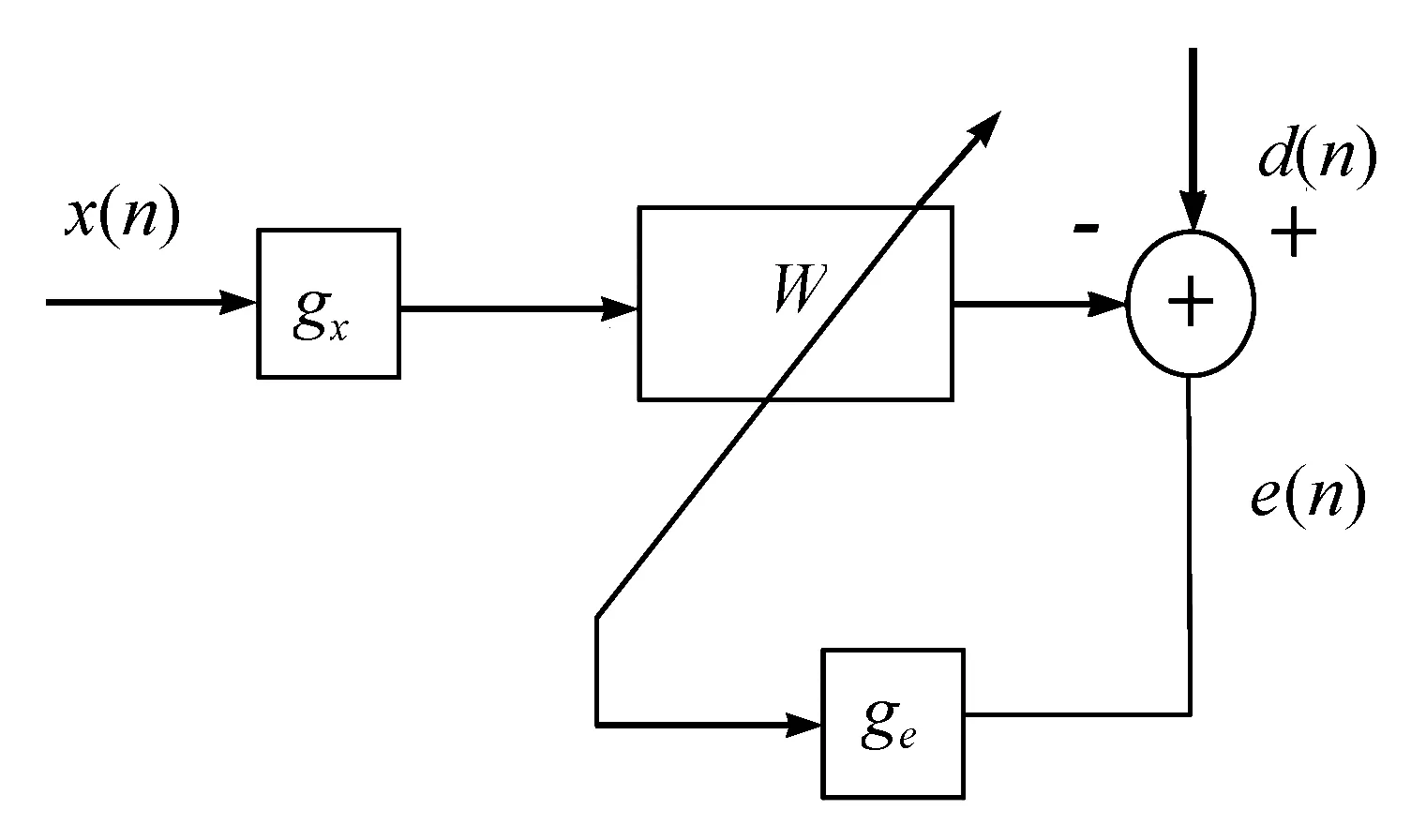
图1　基于非线性变换的自适应滤波

图1中gx(.)和ge(.)分别代表输入信号x(n)和误差e(n)的非线性变换函数,d(n)代表期望信号,经过变换后,代价函数变得有界。因此可以得到自适应滤波器权值向量w(n)的迭代公式:

(1)

式中μ为步长。

图2为噪声非线性变换有源控制系统,图中NLT 为非线性变换环节,W(z)为有限脉冲响应的横向结构型滤波器[7]。

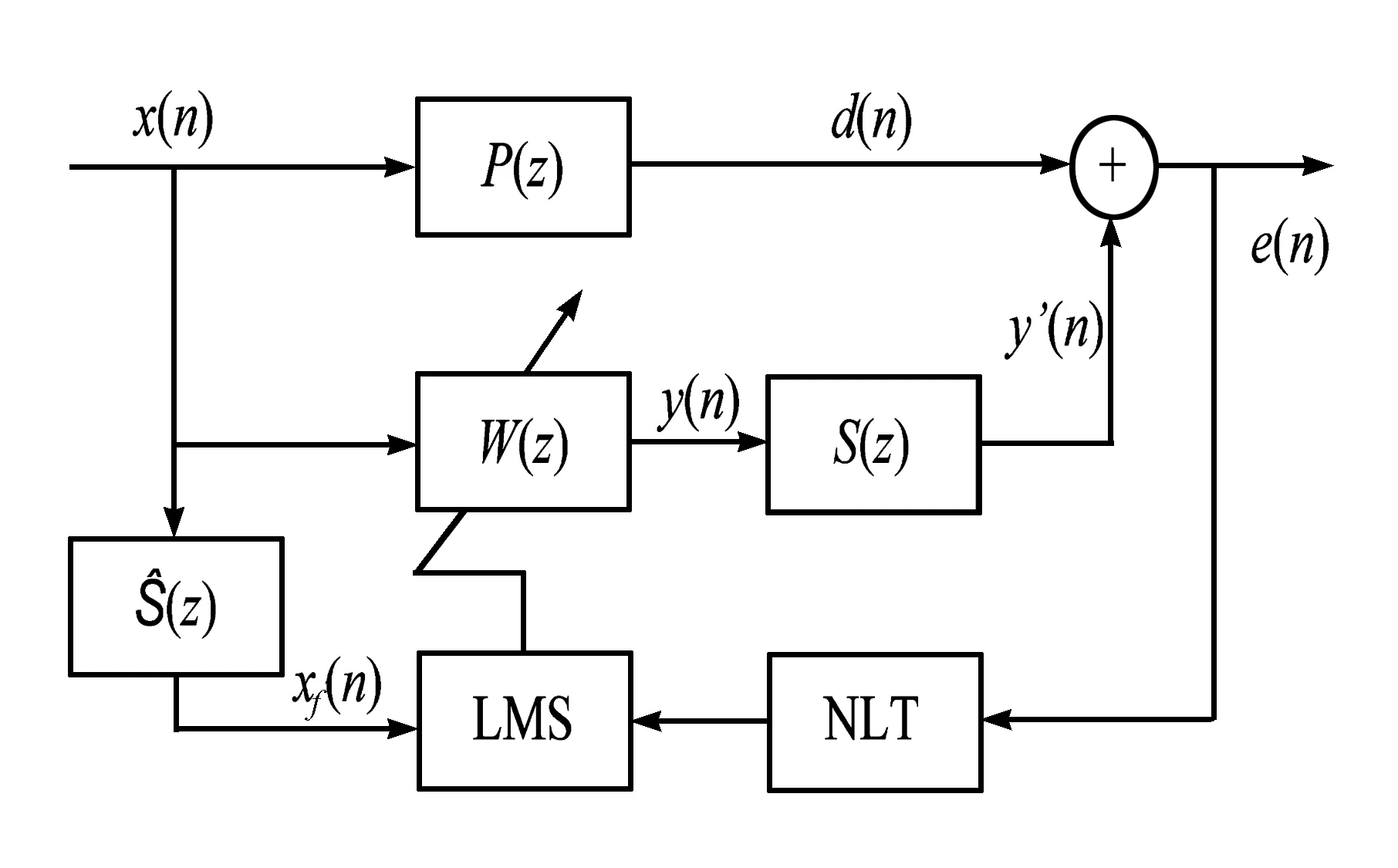
图2　噪声非线性变换有源控制系统

2.1FxlogLMS算法

由文献[8]可知:FxlogLMS算法是α稳定分布的噪声信号对数变换阶矩有限的过程,定义目标函数为

(2)

当|e(n)|趋近于零,log|e(n)|趋近于无穷大,而脉冲噪声信号的幅值通常都较大,所以通常的解决方法是当|e(n)|≤1时就取|e(n)|=1。可以看出公式(2)的定义和特征指数α无关,因此不需要α的相关先验信息,无需预先选择阈值参数。参照FxLMS算法推导出:

(3)

由此得到权值向量更新公式为

(4)

从式(4)中可看出:当|e(n)|趋近于∞时,limlog|e(n)|/|e(n)|=0,|e(n)|越大,滤波器更新系数就越小,这样当脉冲信号中高幅值尖峰信号出现时,算法始终能保持良好的稳定性。比较FxLMP算法,当|e(n)|>1,且log|e(n)|/|e(n)|=1时,FxlogLMS算法近似可看成是p=1的FxLMP算法；当|e(n)|很大时,算法更新系数log|e(n)|/|e(n)|非常小,而此时FxLMP算法中的更新系数p|e(n)|p-1依然较大,这样比较来看,同样是处理大幅度高尖峰脉冲信号,FxlogLMS算法受到的影响要远小于FxLMP算法,因而具有较好稳定性。

2.2FxatanLMS算法

FxatanLMS算法是噪声信号反正切变换阶矩有限过程[8],目标函数定义为

(5)

定义y=arctan(x),反正切函数是单调递增奇函数。

(6)

故式(5)可写成:

(7)

类似于FxlogLMS算法,可计算得到该算法权值向量更新公式为

(8)

可以看出,公式(5)的定义和特征指数α无关,因此不需要α的相关先验信息,不需要预先选择阈值参数。此算法与 FxlogLMS算法相比,当|e(n)|趋近于∞时, 两种算法都将收敛于0,但可以看出式(8)里的分母e2(n)增大速度明显高于|e(n)|,所以FxatanLMS算法收敛速度将优于FxlogLMS算法；又当|e(n)|≤1时,FxlogLMS算法中,取|e(n)|=1,设置了固定阈值,使得log|e(n)|/|e(n)|=0,这样进行设置之后,会出现一段死区。在这个区间,算法停止更新。影响了噪声控制效果,使算法收敛速度下降,而arctan(e(n))/(e2(n)+1)是连续变化的,充分利用了各个样本点信息,保证了算法具有良好的稳定性和收敛速度[9-10]。

2.3FxSigmodLMS算法推导

基于Sigmoid函数非线性转换的算法称为FxSigmoidLMS算法[11-12]。Sigmoid函数是一个非线性连续函数,其形状如“S”,FXSigmodLMS算法是噪声信号“S”型变换阶矩有限过程。目标函数定义为

(9)

(10)

经过Sigmoid函数非线性变换后,过程具有了有限二阶矩。同样可以看出,公式(9)的定义和特征指数α无关,因此不需要α的相关先验信息,不需要预先选择阈值参数。类似于FxlogLMS算法可计算得到算法权值向量更新公式为

(11)

公式中:

公式(11)可改写为

(12)

设定:

FxLMS算法权值向量更新公式为

(13)

比较公式(12)和(13)可以看出:FxSigmoidLMS算法可以解释为时变步长FxLMS算法。时变步长可以定义:

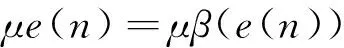
(14)

当|e(n)|越大,滤波器系数越小；当|e(n)|趋近于∞,lim(β(e(n)))=0。因此,FxSigmoidLMS算法对于脉冲噪声具有更强的鲁棒性。算法以一个连续模式更新滤波器系数,具有更好的消噪性能[13-14]。

3　非线性变换FxSigmodLMS算法计算机仿真

图3—图5为特征指数α1=1.3、α2=1.5、α3=1.7时, FxSigmodLMS算法的计算机仿真中主噪声d(n)、抗噪声y′(n)和残差信号e(n)的变化曲线。仿真图显示:随着迭代次数的增加,残差信号越来越小,消噪效果越来越明显。

图3　主噪声、抗噪声、残差信号(α=1.3)

在信号分析中,由于无法用数学关系准确地对随机变量均方值进行度量,所以常使用“功率谱密度”概率统计方法。仿真中使用Welch功率谱密度估计(幅频响应)对比抗噪前后效果,FxSigmodLMS算法的仿真得到的幅频响应曲线见图6。由图6可知,抗噪后的噪声得到了有效的衰减。

图4　主噪声、抗噪声、残差信号(α=1.5)

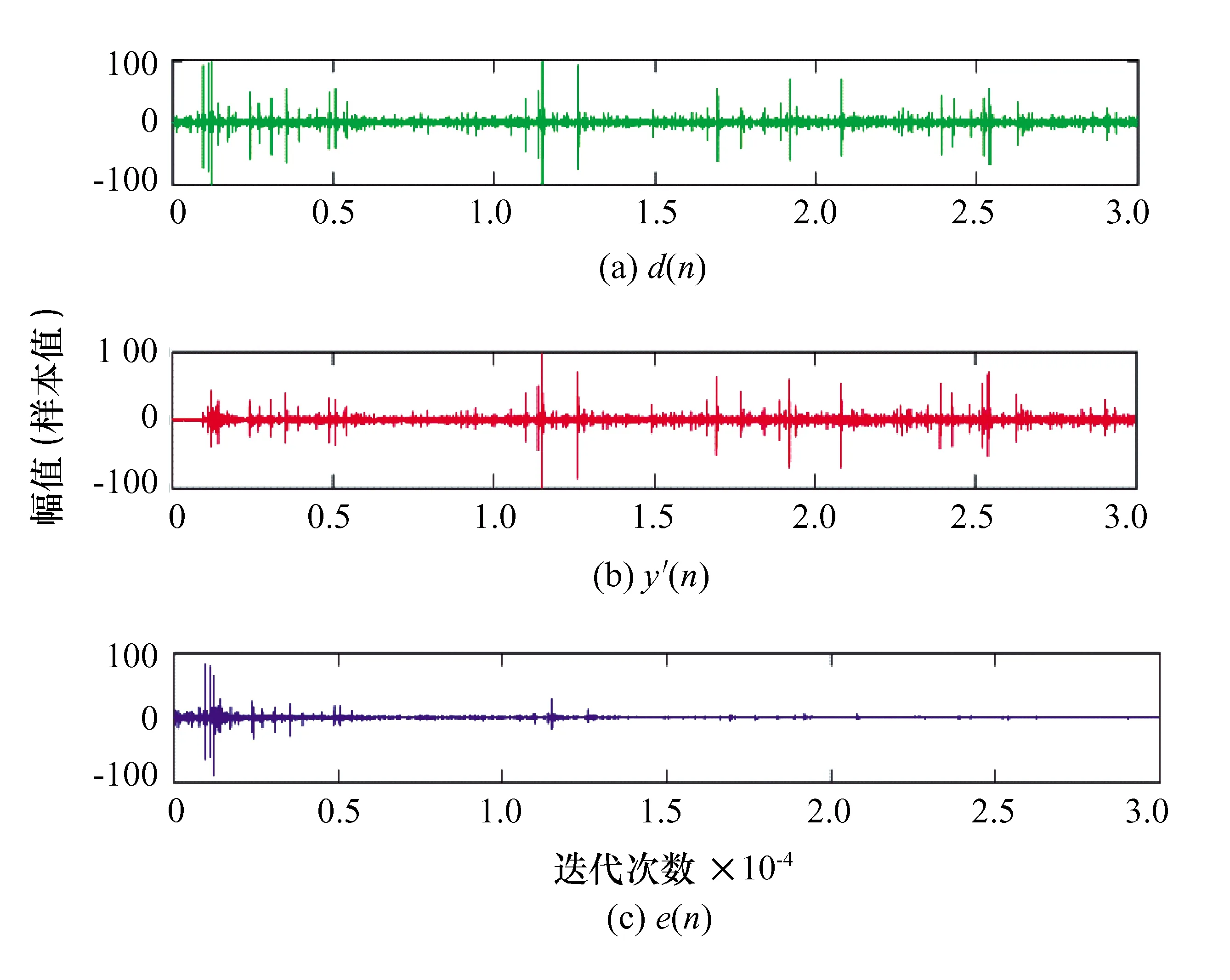
图5　主噪声、抗噪声、残差信号(α=1.7)

图6　FxSigmodLMS算法仿真得到的幅频响应曲线

4　结语

对脉冲噪声进行非线性预处理,然后再利用LMS算法,计算量大幅度减少,保证了算法较快的收敛性能。Matlab仿真结果证实了非线性变换脉冲噪声算法消除噪声的有效性。主噪声、抗噪声、残差信号仿真图显示了算法有良好的消噪效果。Welch功率谱密度估计得到了令人满意的效果。基于非线性变换脉冲噪声算法可进行连续更新,不需要事先估测阈值,有较好的快速性。今后将在以下几方面进一步发展:

(1) 算法采用的是有限横向结构的脉冲响应FIR,那么这些算法是否适合应用于无限的FIR将是一个努力研究的方向。

(2) 算法框架都是基于LMS结构的,从自适应滤波理论可以知道,相对于LMS结构,RLS结构算法的收敛速度要快好几倍,稳态误差在理论上能达到收敛于零的效果。同样效果的还有FAP(射投影)算法,所以研究现已有算法的其他两种结构算法的改进非常具有实际意义[15]。

References)

[1] 宋秀丽,尤庆伟,夏杰.脉冲噪声对工人听力影响的观察[J].河南预防医学杂志,2008,19(6):418-419.

[2] 邱天爽,张旭秀.统计信号处理:非高斯信号处理及其应用[M].北京:电子工业出版社,2004.

[3] 吕晓蕊.Alpha稳定分布的模型仿真及参数估计[D].武汉:华中科技大学,2008.

[4] 高红武.噪声控制技术[M].武汉:武汉理工大学出版社,2009:1-11.

[5] 刘洪.有源噪声控制算法及实验研究[D].哈尔滨:哈尔滨工程大学,2009.

[6] 周亚丽,张奇志,邵俊.冲击噪声的有源控制方法综述[J].北京信息科技大学学报,2011,26(5):33-38.

[7] 吴礼福.脉冲噪声自适应有源控制算法研究[D].南京:南京大学,2012.

[8] Wu Lifu, He Hongsen, Qiu Xiaojun. An active impulsive noise control algorithm with logarithmic transformation[J].IEEE Trans on Audio Speech and language processing 2011,19(4):1041-1044.

[9] 邵俊,周亚丽,张奇志.有源脉冲噪声控制的反正切变换算法[J].噪声与振动控制,2012(2):27-31.

[10] Zhou Y L,Zhang Q Z,Li X D,et al.On the use of an SPSA-based model-free feedback controller in active noise control for periodic disturbances in a duct[J].Journal of Sound and Vibration,2008,317(3/4/5):456-472.

[11] 周亚丽,张奇志.有源噪声与振动控制:原理、算法及实现[M].北京:清华大学出版社,2014.

[12] 李沛,宋晓娜,侯晓霞,等.基于S型函数的α稳态分布脉冲噪声有源控制[J].实验室研究与探索,2014,33(6):29-32.

[13] Zhang Zhiyi,Chen Yong,Li Hongguang,et al.Simulation and experimental study on vibration and sound radiation control with piezoelectric actuators[J].Shock and Vibration,2010(17):1-12.

[14] Akhtar M T,Mitsuhashi W.Improved adaptive algorithm for active noise control of impulsive noise[J].ICSP2008Proceedings,2008(24): 2669-2702.

[15] 里红杰,基于分数低阶循环相关的系统辨识及应用研究[D].大连:大连理工大学,2007.

Research active control algorithm based on nonlinear transform of impulsive noise

Li Pei, Zhang Jingrong

(Mechanical and Electronic Practice Center, Beijing Information Science and Technology University , Beijing 100192, China)

The alpha stable distribution provides a strong theoretical tool for the analysis of the non-Gaussian impulsive noise signals.Active control of symmetric α stable distribution impulsive noise is studied. Impulsive noise algorithm based on nonlinear transform is derived and analyzed, the computer simulation was carried out to validate FxSigmod algorithm. Simulation results prove the effectiveness of the algorithm. It does not need the parameter selection and thresholds estimation.it is easy to implement.Continuous update performance of algorithm is good, which can restrain impulsive noise quickly and efficiently.

impulsive noise； nonlinear transform； active control;αstable distribution

10.16791/j.cnki.sjg.2016.03.011

2015- 10- 09修改日期:2015- 10- 30

北京市教育委员会科技计划面上项目(KM201511232023)

李沛(1971—),女,吉林伊通,硕士,高级实验师,主要研究方向为噪声与自适应控制.

E-mail:lipei711215@sina.com

TB535

A

1002-4956(2016)3- 0039- 04