基于混沌差异进化算法的有功优化仿真研究

陈功贵, 陆正媚, 郭艳艳, 郭　飞, 唐贤伦

(1. 重庆邮电大学 自动化学院, 重庆　400065；2. 武汉铁路职业技术学院 机车车辆工程系, 湖北 武汉　430205)



基于混沌差异进化算法的有功优化仿真研究

陈功贵1, 陆正媚1, 郭艳艳2, 郭飞1, 唐贤伦1

(1. 重庆邮电大学 自动化学院, 重庆400065；2. 武汉铁路职业技术学院 机车车辆工程系, 湖北 武汉430205)

差异进化(differential evolution,DE)算法在求解电力系统有功优化的问题上易陷入局部最优,因此在其基础上引入混沌算法的Logistic映射,形成混沌差异进化(chaotic differential evolution,CDE)算法。该算法在迭代后期,使固定取值的搜索步长和交叉算子在一定范围内随机取值。为验证算法的实用性,利用Matlab软件,将DE和CDE在IEEE30节点测试系统上进行电力系统有功优化仿真。仿真结果表明,CDE算法扩大了搜索范围并且增加了种群多样性,能获得搜索质量更高的最优解,即考虑阀点效应的燃料费用更低。通过此次仿真,既可加深学生对有功优化的认识和理解,又可提高学生运用仿真技术为改进算法提供理论依据与评价的能力。

电力系统仿真; 有功优化； 混沌差异进化算法； Matlab

电能是国民经济与生活的主要动力,因此提高电力系统的安全性、可靠性以及经济性尤为重要。频率是衡量电能质量的关键指标,其与有功功率相关,有功功率是否平衡,是否合理分配也就直接影响电力系统安全运行,所以有功优化是电力系统运行的重要控制方式[1-3]。由于系统结构的复杂性,有功优化问题成为了一个非线性、多约束、包含离散变量的全局优化问题。

差异进化算法(differential evolution,DE)是一种简单的基于随机种群的搜索方法,被成功应用于现实生活中很多全局优化问题[4-6]。将DE算法与混沌算法的Logistic映射相结合,形成混沌差异进化算法(chaotic differential evolution,CDE)。CDE算法保留了DE算法的3个算子,即变异算子、交叉算子以及选择算子,在算法迭代后期,用Logistic映射改变DE算法里固定取值的搜索步长F和交叉算子CR,由此增加了种群多样性。为了验证算法的实用性和高效性,利用Matlab软件[7-10],将DE和CDE算法在IEEE30节点测试系统上分别进行20次电力系统有功优化仿真。该测试系统包含41条支路、21个负荷节点、6台发电机、4台变压器和9台无功补偿装置,具体数据见文献[11-12]。由有功优化的数学模型可知,该仿真有24个控制变量,即种群内的每一个粒子为24维列向量。仿真结果表明,CDE算法不仅能够使有功优化问题得到收敛,还能找到比DE算法更为理想的最优解。Matlab仿真结果中包含大量的实验数据和仿真图形,使学生能更牢固地掌握有功优化过程和CDE算法特性。

1　有功优化的数学模型

在电力系统的系统参数及负荷情况都明确的情况下,有功优化就是改变发电机的有功功率输出P、电压幅值V、可调变压器的抽头选择T以及无功补偿器的无功投切C4个参数,使系统安全运行并且使某目标函数达到最优[13]。有功优化的数学模型包含约束条件和目标函数。

1.1约束条件

约束条件又分为不等式约束和等式约束。

等式约束即每个节点的功率平衡:

(1)

式中,QGi,PGi,QLi,PLi分别代表节点i的发电机的无功功率输入、有功功率输入、负荷的无功功率消耗和有功功率消耗；Gij为节点i、j间的电导；Bij为节点i、j间的电纳；Vi为节点i的电压幅值；δij为节点i、j间的电压相角差；n为电力系统的节点数。

不等式约束条件:

(1)节点的电压幅值:

(2)

(2) 发电机的有功功率与无功功率:

(3)

(3) 各支路视在功率:

(4)

(4) 变压器变比:

(5)

(5) 电容器无功补偿:

(6)

式中,QCi为第i台无功补偿器的无功投切,NG为发电机数,NB为支路数,NT为变压器数,NC为无功补偿器数。

1.2目标函数

在本文研究中,优化的目标函数为考虑阀点效应的燃料费用f为

(7)

(8)

式中fi是每台发电机考虑阀点效应的燃料费用,ai、bi、ci、di和ei分别是发电机燃料费用系数。

控制变量在给定时就满足系统约束条件。为了使状态变量也满足,就引入了罚系数。罚系数将惩罚超过约束的状态变量,越限越多,其目标函数值越大,即适应值越差,就越容易被淘汰,其构成的目标函数F为

(9)

式中,KV为节点电压越限的罚系数,KQ为发电机无功功率越限的罚系数,KS为平衡节点有功功率越限的罚系数,KL为各支路视在功率越限的罚系数。

由目标函数可以看出,罚系数的选择对最终结果影响很大,若取值不当还会导致最优解不满足系统安全运行的约束。为了避免这种情况,本文对罚系数取动态值,其表达式为

(10)

其中:KFk为各罚系数(KV、KQ、KS、KL)在第k次迭代的取值；KFmin、KFmax分别为各罚系数的最小值和最大值,k为迭代次数,kmax为最大迭代次数。

在初期时罚系数的取值较小,随着迭代次数的增加,罚系数的取值也逐渐增大,这样可以减少算法陷入早熟的概率。另外,式中Vlim、Qlim、Plim、Slim是根据因变量的范围而判定:

(11)

2　CDE算法

2.1CDE算法的数学模型

CDE算法的数学模型包含标准DE算法的变异算子、交叉算子、选择算子3个重要算子以及混沌算法的Logistic映射。

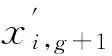
(12)

需要强调的是xr1,g、xr2,g、xr3,g为种群内的不同向量；并且种群内的每一个向量都必须至少参与1次变异。F为搜索步长,为了制定合适的变异扰动范围,其值一般控制在[0,2],通过查阅文献[14],可知在这范围内的搜索步长可能提高算法的收敛性。

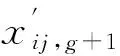
(13)

其中:Np为种群个数；D为每个粒子的维数；CR为交叉算子,一般介于[0,1],该参数可以掌控种群的多样性,并且减少优化中出现局部最优的概率；q是介于[1,D]之间的随机数,为了保证变异后的中间个体至少有一维参与了交叉；x″ij,g+1为经过变异、交叉两项操作后的第g+1代的第i个中间个体。

(3) 选择算子。选择算子在探索最优解时提升种群内个体的适应度。针对父代群体和产生的中间个体,进行一对一的贪婪选择,选择具有更好适应度的个体作为第g+1代新个体,有:

(14)

其中f为目标函数；xij,g+1为经过变异、交叉、选择3项操作后得到的第g+1代的新个体。

(4) 混沌算法的Logistic映射。利用混沌算法的随机性、遍历性和规律性,可以扩大搜索范围,增加种群多样性,避免算法陷入局部最优。混沌现象有很多种形式,其中Logistic映射是由荷兰生物学数学家Verhulstt提出的[15],其表达式为

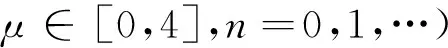
(15)

当μ为4时,为完全混沌。本文就是利用完全混沌现象使DE算法中的F和CR由固定值变为在一定范围内的随机动态值。其表达式为:

(16)

式中k为迭代次数。

需要强调的是,为了避免Logistic映射使参数趋于某一常数,所以在初始化时F与CR不取0.25、0.5、0.75。

2.2CDE算法的求解步骤

DE算法在迭代后期容易出现局部收敛现象,于是在一定迭代次数以后,引入Logistic映射,加强算法的搜索能力,并且增加算法的高效性以及准确性。CDE算法的求解步骤如图1所示。本文中,CDE算法将在迭代次数大于500时引入Logistic映射改变参数F与CR。

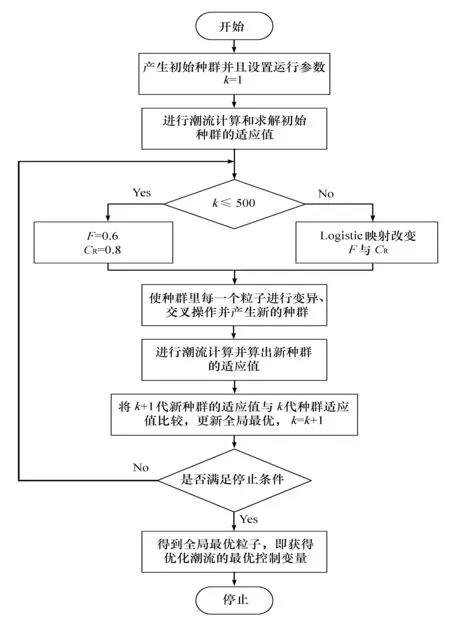
图1　CDE算法的求解步骤

3　基于Matlab的有功优化仿真实验

本文将IEEE30节点的标准测试系统用以测试两种算法的有功优化效果。在仿真开始前, DE和CDE算法的初始参数的设定见表1。

表1　两种算法初始参数设定

其中,Np为种群个数,kmax为最大迭代次数,G为优化次数,F为搜索步长,CR为交叉算子。由于CDE算法中的F、CR为动态随机取值,所以表内省略。程序将每次计算结果都扫描到相应的表格中保存起来,从所得数据中,记录下每种算法的最优值、最差值和平均值,具体数据见表2。

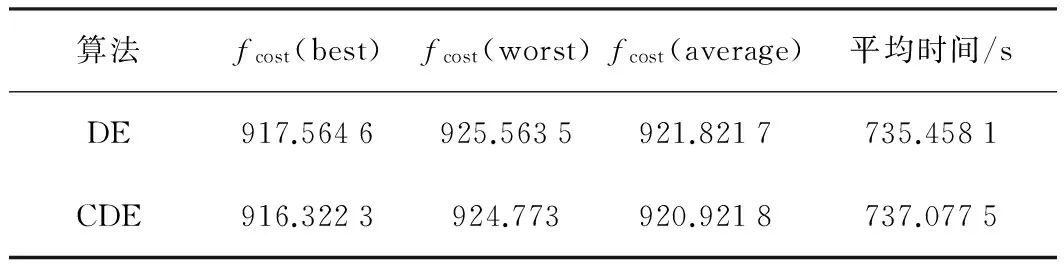
表2　两种算法优化结果比较　$/h

仿真结果表明,CDE算法考虑阀点效应的平均燃料费用和最优燃料费用均比DE算法低,并且用时与DE算法相差甚少,即优化效果与搜索效率均高于DE算法。其中CDE算法每小时的平均燃料费用比DE算法低了0.8999$/h,这个数目从经济角度来看是十分可观的。

根据两种算法20次的运行结果,每种算法的平均收敛曲线见图2,每种算法的最优解收敛曲线如图3。

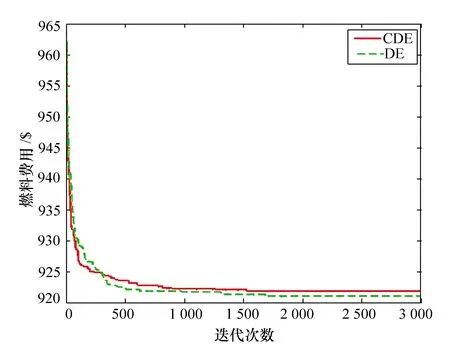
图2　两种算法的平均收敛曲线图

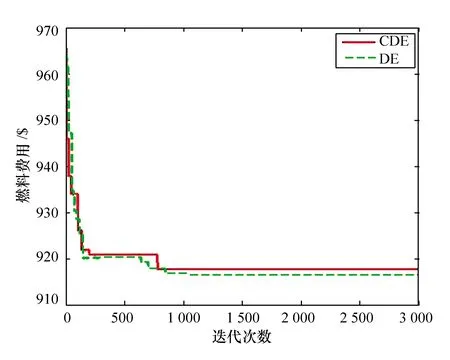
图3　两种算法的最优效果收敛曲线图

由图2和图3可知,两种算法都能使电力系统有功优化问题得到收敛,但CDE算法的收敛结果更优。算法迭代到800代时,DE算法已经找到局部最优值,而CDE算法仍然还在更新全局最优,说明DE算法在迭代后期出现了早熟现象,CDE算法由于局部搜索能力变强,陷入局部最优的概率减小。值得强调的是,两种算法各自选取的结果,其控制变量和状态变量均满足约束条件,即满足系统安全运行。

基于两种算法优化后的最优控制变量见表3和表4。其中P为发电机有功功率输出,V为发电机节点电压幅值,T为可调变压器变比,C为无功补偿器的补偿容量。表中的下标分别对应于IEEE30节点测试系统里的相应节点号；Pi max和Pi min分别代表系统中各发电机的有功功率输出最大值和最小值,Xi max和Xi min分别代表系统中各控制变量标幺值的最大值和最小值。以下数据中的标幺值以100 MVA作为功率基准值。由表3和表4可知,两种算法的最优解均满足系统安全约束。

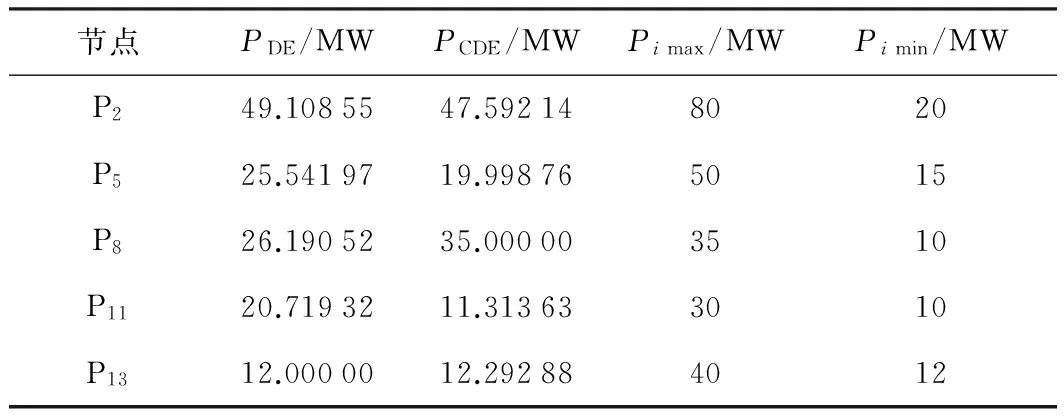
表3　两种算法最优解中的发电机有功功率输出

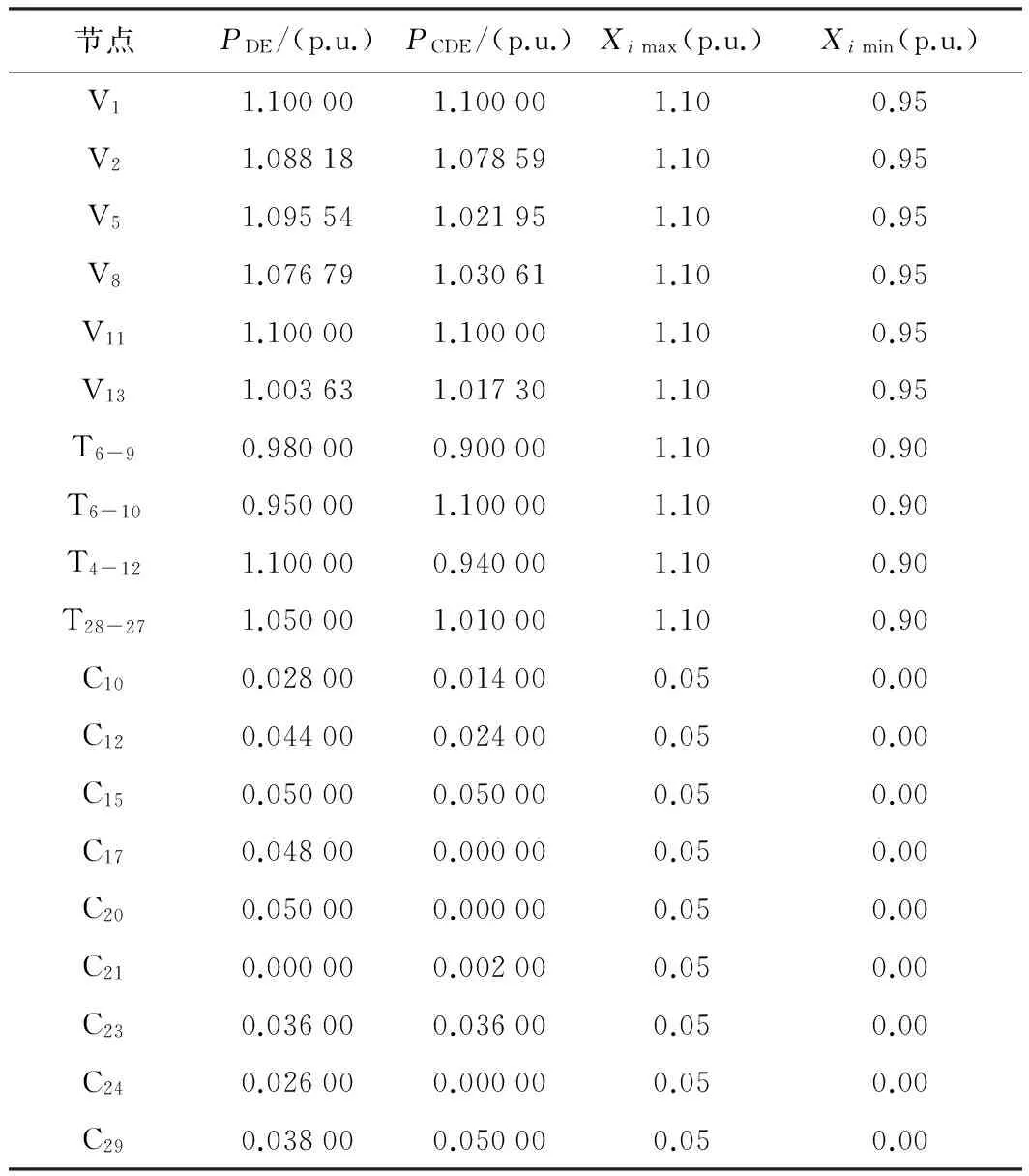
表4　两种算法最优解中的部分控制变量

4　结语

为了避免DE算法求解有功优化问题时陷入局部最优,提出了结合混沌算法的CDE算法,并将此算法成功应用于电力系统有功优化。利用Matlab进行仿真实验,模拟现实生活中的电力系统,通过数据记录和收敛曲线可以直观地看出DE和CDE算法均能在保证系统安全运行的情况下求解优化问题,并且CDE算法具有更好的收敛结果和更高的搜索效率。通过将理论知识和实践仿真相结合,使学生对有功优化的动态过程有了更直观的理解,并对CDE算法有了更深刻的认识。

References)

[1] 刘光晔, 杨以涵. 电力系统电压稳定与功角稳定的统一分析原理[J]. 中国电机工程学报, 2013,33(13):135-149.

[2] 王姗姗, 孙华东, 易俊, 等. 电力系统安全稳定相关标准对大电网的适用性综述[J]. 电网技术, 2013,37(11):3144-3150.

[3] 陈珩. 电力系统稳态分析[M]. 北京: 中国电力出版社, 2007.

[4] 李维刚, 贾树晋, 郭朝晖. 基于分解的多目标差分进化算法及其应用[J]. 信息与控制, 2013,42(3):392-400.

[5] 汪慎文. 差分进化算法研究进展[J]. 武汉大学学报:理学版,2014,60(4):283-292.

[6] 马立新, 孙进, 彭华坤. 多目标差分进化算法的电力系统无功优化[J]. 控制工程, 2013,20(5):953-956.

[7] 陈功贵, 杜阳维, 郭艳艳, 等. 水轮机调速系统抗负荷扰动的动态仿真研究[J]. 实验技术与管理, 2015,32(6):97-101, 105.

[8] 田芳, 黄彦浩. 电力系统仿真分析技术的发展趋势[J]. 中国电机工程学报, 2014,34(13):2151-2163.

[9] 金波. Matlab在动态电路分析中的应用[J]. 实验室研究与探索, 2009,28(11):27-30.

[10] 陈功贵, 黄山外, 郭艳艳, 等. 基于Simulink的风电机组变桨距控制系统仿真研究[J]. 实验技术与管理, 2015,32(8):105-108.

[11] Chen G, Liu L. Chaotic improved PSO-based multi-objective optimization for minimization of power losses and L index in power systems[J]. Energy Conversion and Management, 2014,86:548-560.

[12] Lee K Y, Park Y M, Ortiz J L. A united approach to optimal real and reactive power dispatch[J]. IEEE Trans Power Apparatus Syst, 1985,104(5):1147-1153.

[13] 叶希, 鲁宗相, 乔颖, 等. 风火联运源端系统有功优化运行分层协调思路[J]. 电力系统自动化, 2014,38(20):1-8.

[14] 董宁, 王宇平. 求解约束优化问题的引导多目标差分进化算法[J]. 吉林大学学报:工学版,2015,45(2):569-575.

[15] 王改云, 马姝靓. 典型混沌系统的Matlab仿真实现[J]. 中国科技信息, 2008(3):252-253.

Research on active power optimization based on chaotic differential evolution algorithm

Chen Gonggui1, Lu Zhengmei1, Guo Yanyan2, Guo Fei1, Tang Xianlun1

(1. School of Automation, Chongqing University of Posts and Telecommunications, Chongqing 400065, China; 2. Department of Locomotive and Vehicle Engineering, Wuhan Railway Vocational College of Technology, Wuhan 430205, China)

The differential evolution(DE) algorithm deals with the problem of active power optimization of power system easily to fall into local optimum, for this reason, it is combined with the Logistic mapping of the chaotic algorithm to form the chaotic differential evolution(CDE) algorithm. In later iterations, the search step and crossover of the chaotic differential evolution algorithm are changed from fixed value to a certain range of random value. In order to illustrate the practicability of algorithms, by the Matlab software, using the differential evolution algorithm and the chaotic differential evolution algorithm can implemente an active power optimization simulation on the IEEE30 bus test system. Simulation results show that the chaotic differential evolution algorithm expands the search range and increases the diversity of the population, so it can get the optimal solution of higher quality, namely it can get a lower fuel cost considering the effect of valve point. The simulation experiment can not only strengthen the students’ understanding of active power optimization, but also improve their ability of using the computer technology to provide theoretical basis and evaluation for the improved algorithms.

simulation of power system; active power optimization; chaotic differential evolution algorithm; Matlab

10.16791/j.cnki.sjg.2016.03.010

2015- 08- 28修改日期:2015- 09- 27

重庆邮电大学教育教学改革项目(XJG1522,XJG1416);重庆市高等教育教学改革研究重点项目(132016)

陈功贵(1964—),男,重庆,博士,教授,主要从事电气工程专业的教学和科研工作.

E-mail:chenggpower@126.com

TM732

A

1002-4956(2016)3- 0034- 05