考虑分布式光伏接入的配网联络开关的优化布置研究

李秋平

（国网桐乡市供电公司，浙江 桐乡 314500）

考虑分布式光伏接入的配网联络开关的优化布置研究

李秋平

（国网桐乡市供电公司，浙江 桐乡 314500）

随着分布式光伏并网的增多，基于放射状运行的中压配电网成了多源网络，这样传统的配网联络开关设置方法就需要进行改进。文章通过对光伏出力的等效变换，将其融合进配网负荷曲线中，然后模拟积分中值定理对新的负荷曲线进行合理区间划分，以此划分结合一系列电气量约束、网络拓扑约束、开关操作次数约束等，寻求线路运行损耗最小和停电损失最少。这就是考虑分布式光伏接入的配网联络开关优化布置方法。算例结果表明，文章提出的方法是有效的，值得进一步推广。

联络开关；分布式光伏；配电网；优化布置；负荷曲线

为了保证配电网的供电可靠性和灵活性，一般需在中压馈线上布置一定数量的联络开关。这些开关的设置需考虑初始投资、运维费用、线路损耗、停电损失、负荷变化等多重因素，可谓复杂万分。

在智能电网逐渐兴起的当下，分布式光伏电源大量接入配网，改变了传统配网的单电源放射状供电模式，即网络成为了多源网络。另外，光伏出力是不稳定的，接入位置具有多样性。这些都增加了含PV配网联络开关优化布置的难度。

为了解决这个问题，文章拟将光伏出力负荷化（即视光伏发电为负向负荷消耗），并与配网正向负荷叠加后一起组成新的负荷曲线，再利用有关负荷不确定性处理方法对负荷曲线进行二次处理，最后综合经济性、可靠性、季节性、时段性等因素，建立考虑分布式光伏接入的配网联络开关布置新方法，以期为智能电网的发展而抛砖引玉。

就国内外研究现状来说，负荷不确定性处理方法主要有基于模糊聚类的曲线分段方法和基于曲线单调的曲线分段方法两大类。文章通过比较，认为后者更具时效性、直观性，但需增加动态环节。

1　总体思路

联络开关的作用是根据运行需要实现网络重构。显然，若某个时段内线路综合负荷（光伏出力与用户负荷的叠加）不变，则联络开关的开合状态也不需改变（假设这之前各联络开关的开合状态已处在最优化情况）。那么，我们所面对的问题的实质就是：对于一个特定网络，在候选的联络开关安装点集合中找出最佳的安装点位置，使得这种安装方法能契合线路综合负荷的变化，即在联络开关动作次数限值范围内通过不断操作联络开关能让线路始终运行在可靠和经济的区间里。

这就涉及到联络开关对光伏-负荷等效曲线的的有效辨识上。具体来说，就是要对综合负荷曲线进行合理分段，每段产生一个等值负荷（类似拉格朗日中值定理），由这些等值负荷来参与相关模型的计算［1］。显然，曲线分段不能过多（过多会产生运算维数灾），也不能过少（过少会影响优化效果），因此需经历一个基于反馈的控制过程。图1所示为本研究课题的大致思路。

图1　考虑光伏接入的配网联络开关优化布置思路

2　光伏电源出力的计算

与集中式大电源相比，光伏电源出力具有明显随机性。笔者参考相关文献，得到光伏出力公式［2］：

式中，t为整点时刻；μ、Iμ（t ）分别为天气状态变量和某一天气下的光伏电源时序出力，maxIμ为在某一μ下的最大光照强度，maxμ为天气变量数目，Pμ为μ的概率。

显然，光伏出力的季节性变化明显。以浙江桐乡的春季为例，取光伏渗透率25%，取晴、阴、雨的出现概率分别为0.4、0.3、0.3，利用式（1）得到如图2所示的光伏出力曲线。该曲线与线路的实际负荷曲线相叠加，就形成光伏-负荷等效曲线。

图2　以浙江桐乡为例的春季的光伏出力曲线展示

3　光伏-负荷等效曲线的初步分段

首先依据经验设定一个初始分段数KS，然后依次进行以下步骤：

（1）划分曲线的单调区间，对各单调区间求积分中值，以该值所对应的横坐标为分段点，记录此时的分段段数，不妨以Num表示。

（2）辨别负荷跃增时段，并将其隔离。方法：计算曲线各相邻整点时刻的负荷差值绝对值Ka，并统计出最大值Kmax；若步骤（1）中确定的某个时段的中值点是曲线极值点且其两侧变化率超过Kmax，则认为该时段出现负荷跃增，应予以隔离。

（3）比较经历步骤（2）后的Num值与KS的大小。若前者大，转步骤（4），反之转步骤（5）。

（4）时段合并。设最新的剔除跃增量的时段划分数为Num，求该情况下所有相邻段的等效中值之差的绝对值。选取绝对值最小的那对相邻时段（不妨用i段、i-1段表示），将其合并为“i-1”段，相应的从“i+1”段起段标号都减1。这样Num=Num-1。时段合并的过程需持续到Num=KS，才能转到步骤（5）。

（5）输出分段点的时间坐标及分段数KS。

4　综合建模

联络开关的布置优劣体现在正常时段的运行线损减少上和故障时段的电量损失减少上。当光伏接入后，需额外考虑晴、阴、雨等不同天气状况的影响因素，因此确立如式（2）所示的综合目标函数及其组成。

式（2）中，f1、f2分别指年运行线损和年停电损失的下降量，w1、w2为权重；ta为季节类型a所占天数；Lj为j时段长度；N为网络节点数；Tp为节点p停电时间下降值；E（ΔENSp）为联络开关的安装给p点带来的停电减少期望；CLp为p点单位时间的停电损失；Pavp为j时段内p处的等值功率。

关于模型的约束条件，主要涉及电气安全和经济可行两大层面，细分为6个小点［3］：①节点电压约束，即节点电压不越标准上下限；②功率平衡约束，即注入节点的P、Q与节点电压、支路导纳等参量的关系符合相关公式；③可靠性约束，即网络可靠性需达到规定指标；④网络拓扑约束，即运行时保持放射状、不出现环网；⑤开关分合次数约束，包括各时段内的所有开关总动作次数和的约束和单台开关单日总动作次数约束两方面；⑥初投资约束，即安装设备总价不能大于投资上限。

5　等效负荷曲线时段划分的调整

我们用Nstmax表示开关动作次数上限、用Nstotal表示开关实际动作次数。在运用上文研究成果进行寻优过程中，若发现Nstmax-Nstotal≥2，说明开关至少还可分-合1次，也间接表明原等效负荷曲线的分段可能还有改进的空间（前已述及，开关是否动作由负荷决定）。因此应尝试对原方案进行修正，步骤如下。

（1）寻找原方案中的一个时段划分，要求该段内的Pmax-Pmin在所有段中是最大的，然后判断这段曲线的单调性。若单调增或单调减，则将该段一拆为二，分段处为中间点，并记KS=KS+1；若不是单调，则采用文章第3小节的方法进行处理。

（2）根据新的等效负荷曲线分段方案，重新进行开关寻优模型计算。之后判断Nstmax-Nstotal，若其小于2，认为已得到最优解，否则重复以上步骤。

6　算例

为保证算例的客观性和普适性，选取IEEE 33节点系统作为计算基础，其拓扑如图3所示，其1～32支路标号及阻抗、负载功率等数据见参考文献［4］。几个假设：①相邻两节点间的线路均设有分段开关；②可以安装联络开关的始末节点集为“3、7”、“11、21”、“8、14”、“20、32”、“15、20”、“15、23”、“17、28”，以上待选的始末节点之间的虚拟支路编号为33～39；③光伏电源容量统一为300kW。

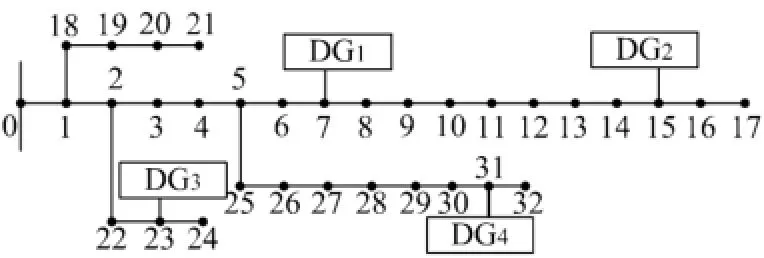
图3　含光伏接入的IEEE 33节点网络

考虑到光伏出力的气候性以及气象资料获取的方便性，笔者选择工作所在地浙江桐乡某乡镇作为算例中光伏运行的地理背景。

因光伏发电的季节性变化明显，因此要得到最合理的联络开关配置方案，必须综合春、夏、秋、冬四季的运算结果。但各季的运算步骤实际是相似的，以及篇幅所限，文章将重点就包含4个光伏电源的IEEE 33节点系统置身桐乡春季气候条件下（桐乡春季的气候指数以及光伏出力曲线见文章第2小节）的联络开关配置进行描述，步骤如下。

（1）参照桐乡实际，设定KS=4，Nstmax=20，w1=0.7，w2=0.3，网络故障率0.045次（a·km），故障线路恢复时间为2.2h/次。

（2）运用第3小节方法，得到等效负荷曲线的初始分段（图4），并根据第4小节内容执行寻优计算。

（3）发现Nstmax-Nstotal=20-12≥2，则依照第5小节方法进行分段方案的修正（图5），再执行寻优计算。

（4）发现Nstmax-Nstotal=20-19=1∈（0，2），说明无须进行下一步修正，输出结果，见表1。由表1可知，春节状态下涉及的联络开关安装支路为33、34、36、37。

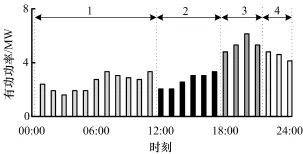
图4　算例线路等效负荷曲线的初始分段

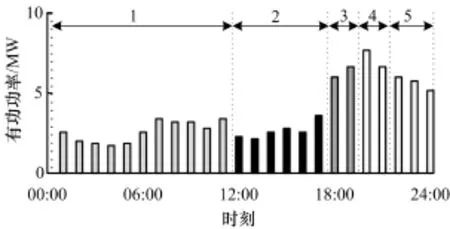
图5　算例线路等效负荷曲线的分段修正

表1　以桐乡春节为背景的IEEE 33节点联络开关布置

将以上步骤（1）至（4）重复运用到夏、秋、冬气候背景下，就能得到3张类似表1的计算结果（具体略）。最后，将四季结果合并，得到基于年周期的最优联络开关安装位置，其始末节点分别为：“3、7”、“11、21”、“20、32”、“15、20”、“15、23”。算例的技术经济效益见表2。

7　技术经济比较

从本质上讲，文章所构建模型的主要特点是采用了基于曲线单调并增加动态环节的等效负荷曲线分段方法。为了彰显该方法的科学性，笔者另外采用了模糊聚类分段（方法参照文献［5］）和不分段两种方法对等效负荷曲线进行处理并执行寻优计算（网络参数、气候条件同算例），得到的技术经济指标列示在表2中。可以看出，文章所推荐方案虽然在初投资方面不是最优，但综合经济效益和供电可靠性均优于其他方案，长期效益明显，值得推广。

8　结论

光伏电源接入配网给配网建设增加了许多不确定性。针对光伏渗透率较低的情况，文章提出将光伏出力拟合进负荷曲线以形成新的等效负荷曲线。通过对该负荷曲线的动态分段处理，能让基于电气安全和经济可行的配网联络开关优化布置数学模型的计算效率得到大幅提升，且优化效果比较明显。笔者也注意到，若光伏渗透率较高，光伏的随机性将左右等效曲线的形状，这时不宜再采用分段的方法来处理负荷曲线。这将是下一步研究的重点。

［1］ 刘巍. 变电站站址优化与配网开关优化配置的研究［J］. 郑州大学学报， 2014， 31（2）： 132-135.

［2］ 许丹， 唐巍. 多目标分阶段中压配电线路开关优化配置［J］. 电力系统保护与控制， 2009， 37（20）： 47-52.

［3］ 陈炜， 艾欣， 吴涛， 等. 光伏并网发电系统对电网的影响研究综述［J］. 电力自动化设备， 2013， 33（2）：26-32， 39.

［4］ Wu Y K， Lee C Y， Liu L C， et al. Study of reconfiguration for the distributed generators［J］. IEEE Trans on Power Delivery， 2010， 25（3）： 1678-1685.

［5］ 唐成龙， 王石刚. 基于数据间内在关联性的自适应模糊聚类模型［J］. 自动化学报， 2010， 29（11）： 1544-1556.

Optimal Layout of PV Consider Access to the Distribution Network of Distributed Contact Switch

Li Qiuping
（State Grid Tongxiang Power Supply Company， Tongxiang， Zhejiang 314500）

With increased network distributed PV， radial run-based medium voltage distribution network has become a multi-source network， so the traditional distribution network contact switch setting methods need to be improved. Through the equivalent output of photovoltaic conversion， which is integrated into the distribution network load curve， and then simulate integral value theorem for the new load curve reasonable interval division， this division with a series of electrical capacity constraints，network topology constraints， the number of switching operations constraints， seek lines running minimum loss and minimum power loss. This is to consider access to the distribution network of distributed photovoltaic contact switch arrangement optimization methods. Numerical results show that the article proposed method is effective and worthy of further promotion.

contact switch； distributed PV； distribution network； optimal layout； load curve

李秋平（1984-），男，工程师，本科，主要从事电力系统的运维工作。