基于最大熵原理的顺磁性固体磁化研究

田宝国，王　栋，吴世勇

（海军航空工程学院基础部，山东烟台264001）

基于最大熵原理的顺磁性固体磁化研究

田宝国，王栋，吴世勇

（海军航空工程学院基础部，山东烟台264001）

从最大熵原理出发，在经典和量子2种情况下，研究了顺磁物质的磁化规律，得到了顺磁物质磁化强度的表达式，在高温弱磁情况下，磁化强度与外磁场成正比，与温度成反比，得到的结论与统计物理中的系综理论或最该然分布结论一致。该原理不仅适用于平衡态问题，而且也适用于非平衡定态问题。

熵；最大熵原理；顺磁物质；磁化强度

熵概念作为描述热力学系统的态函数，最早是由Clausius于1865年提出的，并可用之定量解释热力学第二定律。1877年，Boltzman给出了熵的微观意义（统计解释），把熵概念与宏观系统所包含的热力学概率联系起来[1]。1948年，Shannon提出了信息熵的概念，用熵概念来描述信息量的获得[2]。1958年，Kolmogorov发展了熵的概念，作为不确定性的数学度量，将其引入到非线性动力学当中。目前，熵的概念在物理、化学、经济、信息科学等自然科学以及工程技术等许多领域都得到了广泛的应用，甚至被推广到社会科学当中[3-11]。

1 熵及最大熵原理

1.1熵

本文采用信息熵的定义。对于离散系统，假设该系统某个物理量的取值有n个可能结果x1,x2,…,xn，这些可能结果发生的概率分别为p1,p2,…,pn，则系统信息熵的定义为

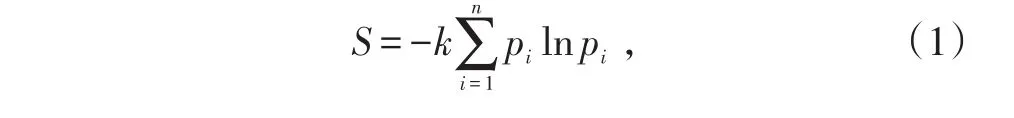
式中，k为正常数。

根据概率性质，pi应满足下面的约束条件：

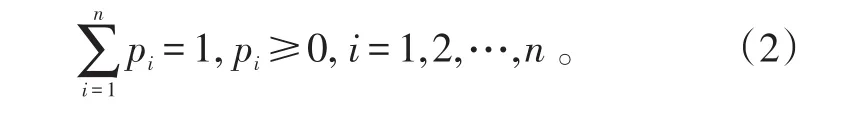
对于物理量可连续取值的概率系统，设变量取值的概率密度为 f(x)，则熵定义为

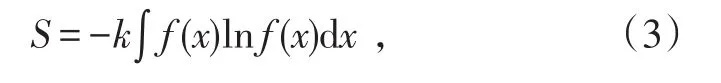
概率密度满足归一化约束条件：

1.2最大熵原理

最大熵原理是1957年由E.T.Jaynes提出的[12]，原理的基本内容可以表述为：一个宏观系统的信息熵在一组约束条件下趋于约束最大值。按照此原理，对于一个宏观系统，如果选择合适的约束条件，然后计算其信息熵在此约束条件下的极大值，就可以求出该系统的微观状态的概率分布。这样就把求系统的分布问题转变为数学上求一定约束条件下的极值问题。作为确定系统分布的重要方法，该原理不仅适用于处理平衡态问题，而且也适用于非平衡定态问题，因而其在物理、化学、交通甚至社会科学等很多领域都得到了广泛应用。本文采用此原理研究顺磁性磁介质的磁化问题。

2 经典情形下顺磁物质的磁化研究

磁矩不为0的粒子（分子、原子或离子）叫做磁性粒子，而由磁性粒子组成的物质叫做顺磁性物质。在没有外磁场作用时，各个粒子的磁矩在空间无规则地取向，它们的磁矩相互抵消，因而物质在宏观上不显示磁性。当顺磁物质处于外磁场中，磁场的作用促使各个粒子的磁矩沿磁场方向取向，但热运动却阻碍这种取向，在这2种作用的影响下，各个粒子的磁矩在空间的取向达到一个平衡分布，粒子的磁矩沿磁场方向取向占优势，因而物质的总磁矩不再为0，即物质被磁化了。如果知道了各个粒子磁矩取向的分布，就可以得到顺磁物质的磁化强度。目前，统计物理教材中得到的分布都是在平衡态前提下由系综理论或近独立系统系统的最概然方法得到。我们认为，在一定的外界条件下，分子磁矩取向的分布应该满足最大熵原理，下面根据此原理来研究该问题。

在经典理论中，粒子磁矩在空间的取向可以连续变化，对于磁矩为μ的粒子，当处于在外磁场H中时，磁势能为

式（5）中：θ为粒子磁矩方向与外磁场之间的夹角；μ0是真空磁导率。

粒子磁矩分布的概率密度定义为 f(θ)，则系统熵为

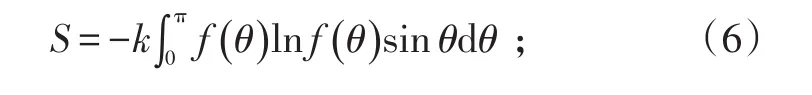
归一化条件表示为

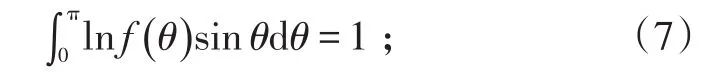
粒子平均磁势能为

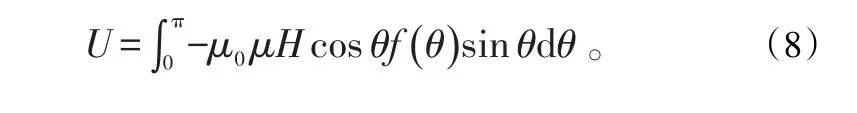
按照拉格朗日乘子法，定义拉格朗日函数为：

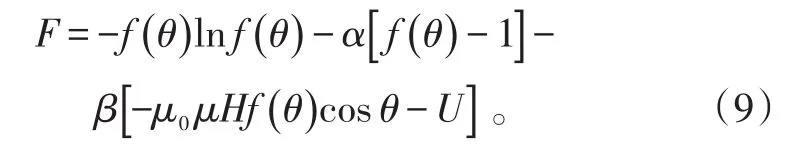
由变分原理，F对 f(θ)的导数为0，可得：

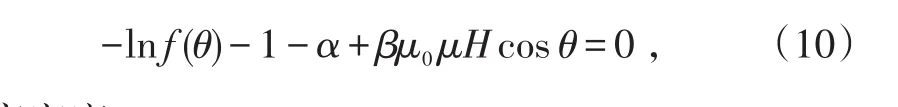
即概率密度

代入归一化条件（7）式得

由式（12）得

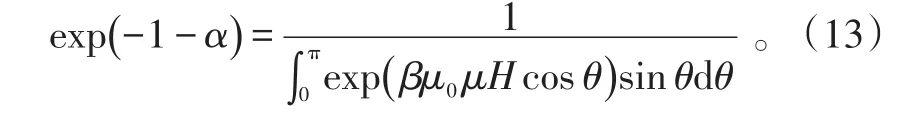
把式（13）代入式（11），可得粒子磁矩方向分布的概率密度为

假设粒子的体密度为n，则系统单位体积内所有粒子的磁矩沿磁场方向的投影之和为顺磁物质的磁化强度M，于是

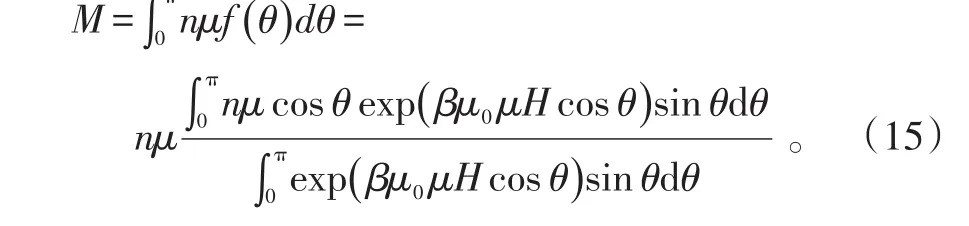
π

令y=βμ0μH，ξ=cosθ，则式（15）可以化为

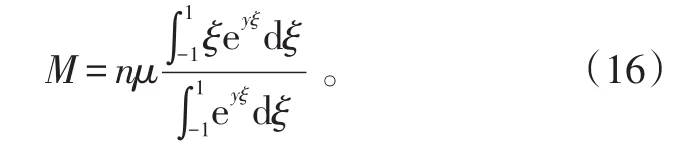
式（16）中的积分结果为朗之万函数L(y)[11]，即：

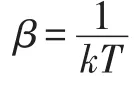
3 量子情形下顺磁物质的磁化研究

量子力学证明，在顺磁物质中，粒子的磁矩与角动量J的关系为[13]

式（19）中：μB是玻尔磁子；g是郎德劈裂因子，

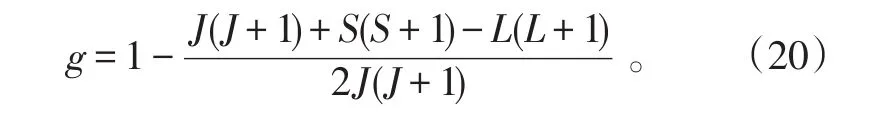
对于一定的粒子，g是一个常数，J是总角动量量子数，L是轨道角动量量子数，S是自旋量子数。

，式中：m是电子的质量；e是电子的电荷；ℏ是约化普朗克常数。

于是，当外磁场为H时，此时粒子在磁场中的磁势能表示为：

式（21）中：mJ是角动量J在磁场H方向上的投影，叫做磁量子数。

mJ只能取-J,-J+1,…,J-1,J这2J+1个值。因为，在量子情形下，粒子角动量的方向只能取离散的数值，此时系统信息熵的定义采用式（1），其中pi为粒子位于某一量子状态的概率。粒子的平均磁势能为

仍然构造广义的拉格朗日函数形式：

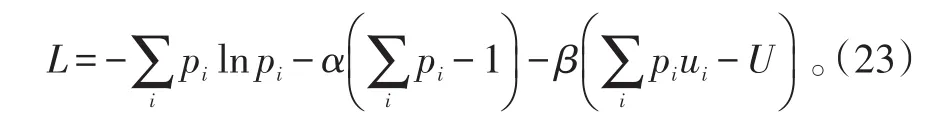
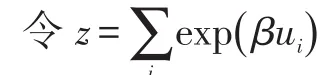
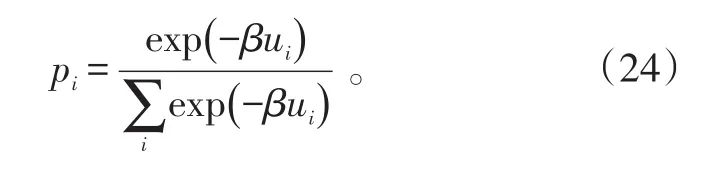
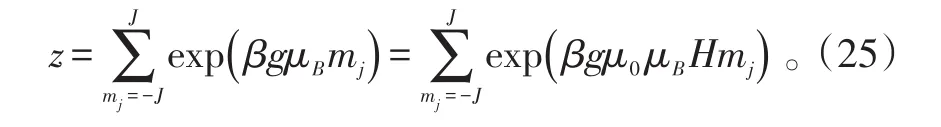
令x=βgμ0μBH，则粒子配分函数为：

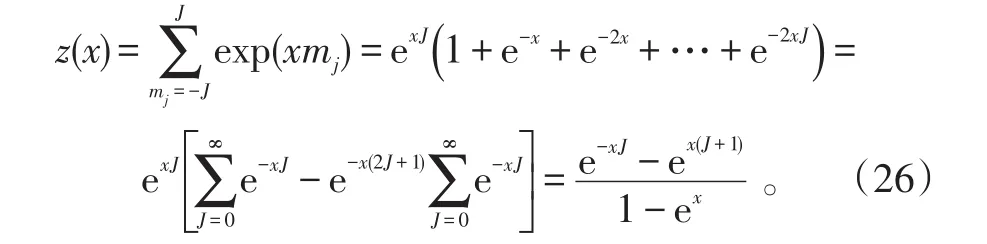
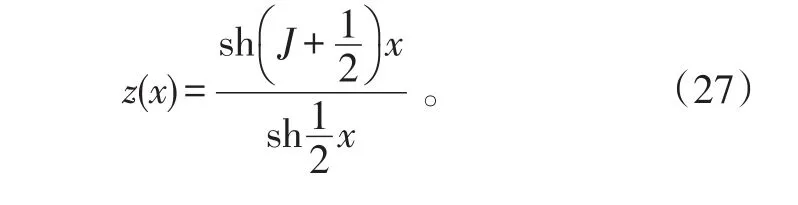
单位体积中粒子的磁矩在磁场方向投影的代数和，即磁化强度为：

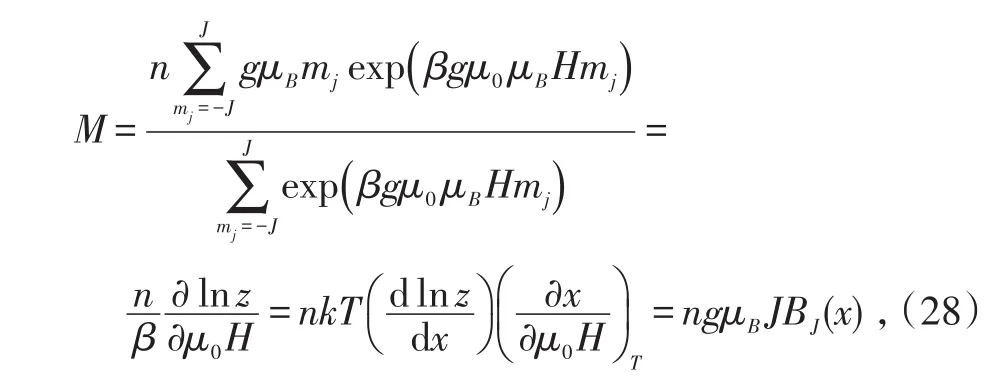
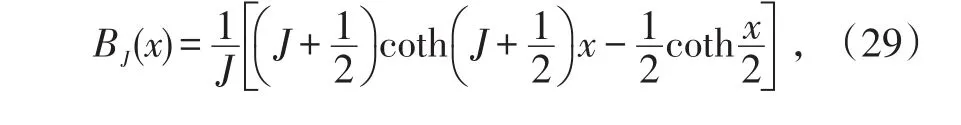
式中，称为布里渊函数。

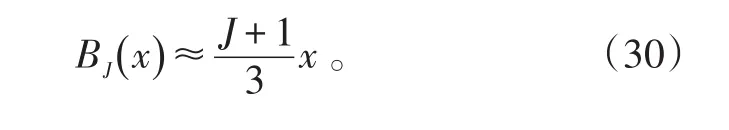
磁矩表达式

这时，所有粒子的磁矩都沿外磁场方向取向，顺磁物质处于磁饱和状态。

4 结论

本文运用最大熵原理研究了顺磁物质在外磁场作用下的磁化规律，在经典和量子2种情况下，得到了系统磁化强度的关系表达式。结果表明，在高温弱磁条件下，磁化强度都与外磁场成正比，与温度成反比；而在低温强磁场情况下，顺磁物质将处于磁饱和状态，此结论与实验结果及统计系综理论得到的结果一致。该研究方法对平衡态系统及非平衡定态系统都同样适用。另外，采用不同熵的定义表达式，可以把该原理方法推广到其他自然或社会系统当中，具有较为普遍的应用范围。

[1]马文蔚.物理学[M].5版.北京：高等教育出版社，2010：247-253.

MAWENWEI.Physics[M].5thed.Beijing：Higher Education Press，2010：247-253.（in Chinese）

[2]SHANNON C E.A mathematical theory of communication[J].ACM SigmobileMobile Computing And Communication Review，1948，5（1）：3-55.

[3]JIANG L.Economic entropy and its applications to the structureof the transportsystem[J].Quality and Quantity，1996，30（2）：161-171.

[4]李鹤龄，杨斌.统计物理方法在离散变量模型中的应用及推广[J].大学物理，2014，33（9）：27-30.

LIHELING，YANG BIN.Applications and extension of statistical physics approach in amodelw ith discrete variables[J].College Physics，2014，33（9）：27-30.（in Chinese）

[5]晋宏营.使用最大熵原理研究电介质系统的极化[J].复杂系统与复杂性科学，2013，10（1）：83-88.

JIN HONGYING.Using maximum entropy principle to study polarization of dielectric systems[J].Complex Systems and Complexity Science，2013，10（1）：83-88.（inChinese）

[6]袁彩霞，王小捷.基于受限最大熵模型的汉语词性标注的研究[C]//第三届学生计算语言学研讨会.沈阳：《中文信息学报》杂志社，2006：303-308.

YUAN CAIXIA，WANG XIAOJIE.Chinese POS tagging using restricted maximum entropy model[C]//3thSymposium on Student Computational Linguistics.Shenyang：Journal of Chinese Information Processing，2006：303-308.（in Chinese）

[7]谭涛，李鹤龄.统计力学基本假设的数学更新[J].大学物理，1997，16（1）：44-45，48.

TAN TAO，LIHELING.Themathematicalupdating of basic hypothesis in statisticalmechanics[J].College Physics，1997，16（1）：44-45，48.（in Chinese）

[8]王栋，朱元甡.最大熵原理在水文水资源科学中的应用[J].水科学进展，2001，12（3）：424-430.

WANG DONG，ZHU YUANSHENG.Principle ofmaximum entropy and Its application in hydrology and water resources[J].Advances in Water Science，2001，12（3）：424-430.（in Chinese）

[9]周旭升，李圣怡，郑子文.基于最大熵原理的平面研抛工艺参数优化[J].中国机械工程，2005，16（11）：1001-1004.

ZHOU XUSHENG，LISHENGYI，ZHENG ZIWEN.Optimization of plane polishing parameters based on maximum entropy principle[J].China Mechanical Engineering，2005，16（11）：1001-1004.（in Chinese）

[10]晋宏营.最大熵原理导出理想气体分子的速度和速率分布[J].科学技术与工程，2012，12（3）：7989-7992.

JIN HONGYING.Using maximum entropy principle to deduce the Velocity distribution of idealgasmolecules[J]. Science Technology and Engineering，2012，12（3）：7989-7992.（in Chinese）

[11]晋宏营.最大熵原理研究二维有极分子电介质的极化规律[J].科学技术与工程，2012，12（10）：2407-2410.

JIN HONGYING.Using themaximum entropy principle to study polarization of two-dimensional dielectric of polar molecules[J].Science Technology and Engineering，2012，12（10）：2407-2410.（in Chinese）

[12]JAYNESR T.Information theory and statisticalmechanics[J].PhysicalReview，1957，106（4），620-630.

[13]王诚泰.统计物理学[M].北京：清华大学出版社，1997：241-243.

WANG CHENGTAI.Statistical physics[M].Beijing：Tsinghua University Press，1997：241-243.（in Chinese）

[14]王鹏，韩敬.朗之万函数与布里渊函数的一些近似公式的推导[J].安庆师范学院学报：自然科学版，2007，13 （2）：87-89.

WANG PENG，HAN JING.Deduce some approximate formulate of langevin function and brillouin function[J]. Journal of Anqing Teachers College：Natural Science Edition，2007，13（2）：87-89.（in Chinese）

Rrsearch on Solid Magnetization of Paramagnetic Substance Based on Maximum Entropy Principle

TIANBaoguo,WANGDong,WUShiyong

（Departmentof Basic Sciences,NAAU,YantaiShandong 264001,China）

Themagnetization law of paramagnetic substance was studied under classical and quantum condition based on maximum entropy principle.The results showed thatmagnetization intensitywas proportional tomagnetic intensity and in⁃versely proportional to temperature underhigh temperature and lowmagnetic intensity,which agreed with to the resultsob⁃tained from ensemble theory ormost probability distribution theory.Maximum entropy principle applied not only to the problem ofequilibrium state,butalso to the problem ofnon-equilibrium stationary state.

entropy;maximum entropy principle;paramagnetic substance;magnetization intensity

O414

A

1673-1522（2016）02-0191-04

10.7682/j.issn.1673-1522.2016.02.018

2015-11-28；

2016-01-19

田宝国（1968-），男，教授，博士。