公式变形，巧解最值

周婷婷

公式变形，巧解最值

周婷婷

看过“变形金刚”系列电影的小朋友，一定羡慕电影里的变形金刚，变成机器人时可以打仗，打不过时还可以瞬间变成汽车逃跑.在《整式乘法》中，我们学习了两数和、差的完全平方公式.这两个公式的不仅可以正向、逆向应用，还应注意它们的一种变形，利用这种变形求解一些最值问题时，干净利落，值得一学.

一、完全平方公式的两个变形

完全平方公式：（a+b）2=a2+2ab+b2和（a-b）2=a2-2ab+b2，

把这两个式子相加、相减，分别得到下面的结果：

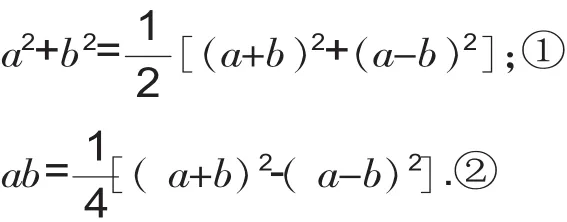
二、利用公式求最大值

例1已知两个自然数的和为8，求这两个自然数a与b乘积的最大值.

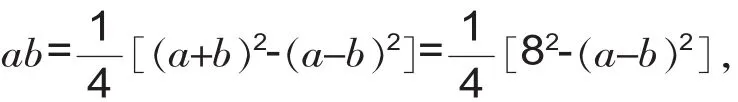
解：根据已知a+b=8，则由变式②得显然，当（a-b）2最小时，ab的最大值为16，这时a=b=4.

注意本题结果的几何意义：周长一定的矩形，当它是正方形时，面积最大.

三、利用公式求最小值

例2已知x+y=4，求x2+y2的最小值.

而（x-y）2≥0，∴x2+y2≥8，故当且仅当（x-y）2=0即x=y=2时，x2+y2有最小值8.

请您把例1和例2比较一下，看看有何异同？

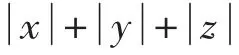
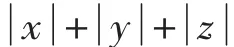
四、利用公式同时求最大值与最小值

例4已知实数x，y，z满足条件x+y+z= 5，xy+yz+zx=3，求z的最大值和最小值.

解：∵x+y+z=5，∴x+y=5-z，于是由xy+ yz+zx=3得12=4（xy+yz+zx）=4xy+4z（x+y），而由变式②可得，xy=［（x+y）2-（x-y）2］，

∴代入上式得

12=（x+y）2-（x-y）2+4z（x+y）

=（5-z）2-（x-y）2+4z（5-z）

≤4z（5-z）+（5-z）2

=-3z2+10z+25，

∵（Ⅱ）无解，