峰回路转识图形——七年级下学期几何重点概念解读

姜红

峰回路转识图形
——七年级下学期几何重点概念解读

姜红

七年级下学期的课本中与几何有关的章节是第七章和第十二章，分别是《平面图形的认识（二）》和《证明》.第七章大致可分为两部分：平行线和三角形.平行线的相关性质和定理是初中几何学习的基础，比如三角形的内角和定理就是依据平行线的相关性质推导出来的.因此可以认为，第七章里前面平行线的相关内容是为后面三角形的内容做铺垫，而多边形内角和、外角和又是三角形相关内容的延伸.整个第七章是一个逻辑严密的整体，它还是八年级学习等腰三角形、直角三角形、平行四边形等内容的基础，是初中几何知识最重要的基础.第十二章《证明》则简要介绍了常见的说理证明的方法.内容比较简略，本文不赘述.为了让同学们更好地掌握第七章的内容，下面给同学们解读一下其中的重要知识点.

重点1：平行线的判定（即直线平行的条件）

关于这个内容，课本共有三条结论：1.同位角相等，两直线平行；2.内错角相等，两直线平行；3.同旁内角互补，两直线平行.其中，结论1是基本事实，是人们公认的真命题，无须证明.结论2和结论3，可以用定理 “对顶角相等”、“同角的补角相等”再经由结论1加以证明，是平行线的判定定理.

例1如图1，直线l1、l2被直线l3、l4所截，下列条件中，不能判断直线l1∥l2的是（）.

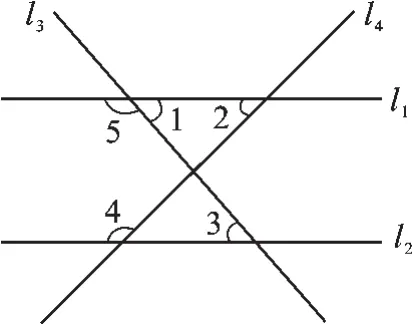
图1

A.∠1=∠3 B.∠5=∠4

C.∠5+∠3=180° D.∠4+∠2=180°【分析】依据平行线的判定的三条结论可知：

A.已知∠1=∠3，根据内错角相等，两直线平行可以判断，故命题正确；

B.不能判断；

C.同旁内角互补，两直线平行，可以判断，故命题正确；

D.同旁内角互补，两直线平行，可以判断，故命题正确.

故选B.

【点评】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两直线平行.

重点2：平行线的性质

平行线的性质定理，课本共有三条结论，合起来可以说成：两直线平行，同位角相等，内错角相等，同旁内角互补.其中“两直线平行，同位角相等”在证明时还初步使用了反证法进行说理（参看教材16页）.后两个定理，可以经由“两直线平行，同位角相等”直接加以证明.

例2 （1）如图甲，AB∥CD，试问∠2与∠1+∠3的关系是什么？为什么？

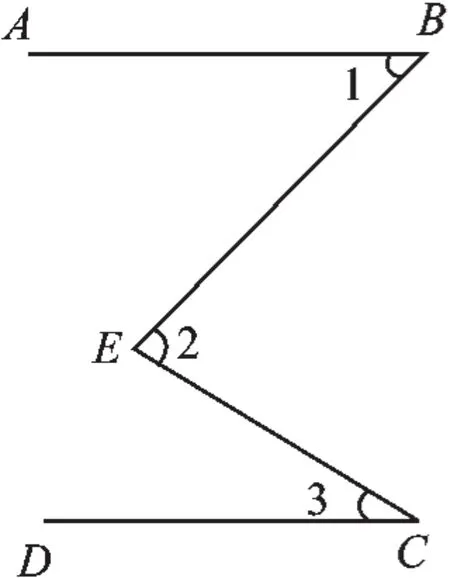
甲

乙

（2）如图乙，AB∥

CD，试问∠2+∠4与∠1+

∠3+∠5一样大吗？为什

么？

（3）如图丙，AB∥

CD，试问∠2+∠4+∠6

与∠1+∠3+∠5+∠7哪

个大？为什么？

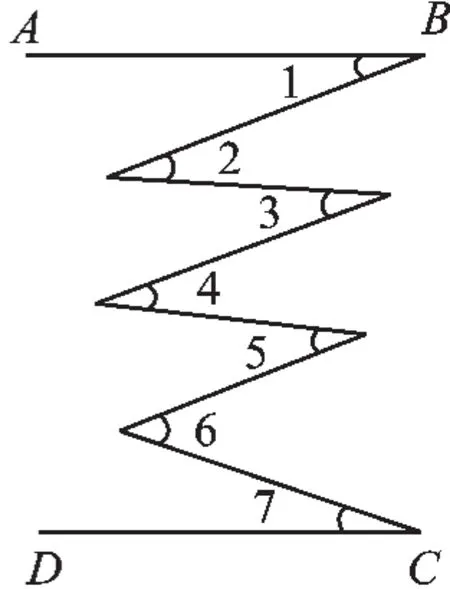
丙

你能将它们推广到一般情况吗？请写出你的结论.

【分析】看这“峰回路转”的折线夹在两条平行线之间，容易联想到内错角这一形象.这样就可以依据“两直线平行，内错角相等”来添加辅助线进行解题.具体解法如下：

（1）∠2=∠1+∠3.过点E作EF∥AB，∵AB∥CD，

∴AB∥CD∥EF，∴∠BEF=∠1，∠CEF=∠3，

∴∠2=∠BEF+

∠CEF=∠1+∠3；

（2）∠2+∠4=∠1+∠3+∠5.

图2

分别过点E，G，M，作EF∥AB，GH∥AB，MN∥AB，

∵AB∥CD，

∴AB∥CD∥EF∥GH∥MN，

∴∠1=∠BEF，∠FEG=∠EGH，

∠HGM=∠GMN，∠CMN=∠5，

∴∠2+∠4=∠BEF+∠FEG+∠GMN+ ∠CMN=∠1+∠EGH+∠MGH+∠5=∠1+ ∠3+∠5；

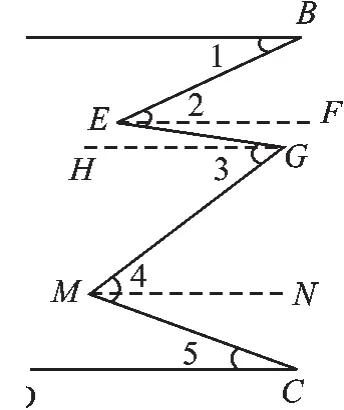
图3

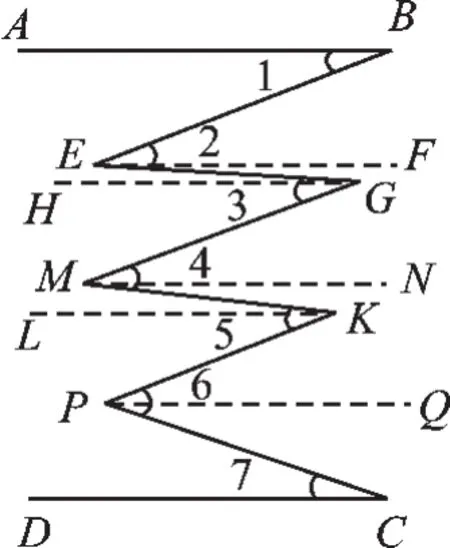
图4

（3）∠2+∠4+∠6=∠1+∠3+∠5+∠7.

分别过点E，G，M，K，P，作EF∥AB，

GH∥AB，MN∥AB，KL∥AB，PQ∥AB，

同（2）可得

∴∠1=∠BEF，∠FEG=∠EGH，∠HGM= ∠GMN，∠KMN=∠LKM，∠LKP=∠KPQ，∠QPC=∠7，

∴∠2+∠4+∠6=∠1+∠3+∠5+∠7.

归纳：开口朝左的所有角度之和与开口朝右的所有角度之和相等.

重点3：图形的平移

图形的平移是初中学习的三种最重要的几何变换之一.另外两种重要的几何变换——轴对称、旋转将在八年级学习.平移的两个要素是方向和距离.这可以分别用具体的方向和距离给出，也可以用一个有向线段给出，比如像“把△ABC平移，使顶点A移动到点A′的位置”这样的说法.图形的平移的结论有：平移前后的图形中，对应点的连线平行（或在同一直线上）且相等.此外，同学们还要掌握平移图形的画法.

例3 如图5，经过平移，四边形ABCD的顶点A移到点A′，做出平移后的四边形.

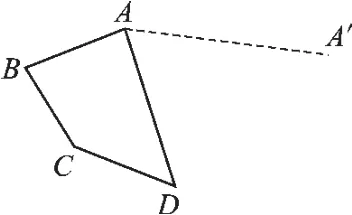
图5

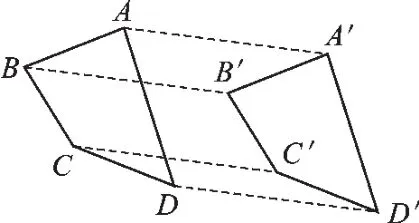
图6

【分析】依据“平移前后的图形中，对应点的连线平行且相等”，过点B、C、D分别作直线AA′的平行线，并在直线上分别截取BB′=CC′=DD′=AA′，再顺次连接A′、B′、C′、D′即可（如图6）.

【点评】考查平移变换作图.关键在于做出平移后的对应点.

重点4：三角形的重要线段

三角形的中线、角平分线、高是三角形的重要线段.解题时要依据其定义，转化为相应的数量关系或者位置关系，再加以运用.通过画图，同学们可以总结出：三角形的三条角平分线交于三角形内一点，三条中线交于三角形内一点.这两个结论的证明比较有难度，将分别在八年级和九年级给出.三角形的三条高（所在直线）交于一点，这点的位置与三角形的形状有关.锐角三角形的三条高的交点在三角形内；直角三角形的三条高的交点在直角顶点；钝角三角形的三条高所在的直线交于一点，在三角形外部.

例4在△ABC中，画出边AC上的高，下面4幅图中画法正确的是（）.

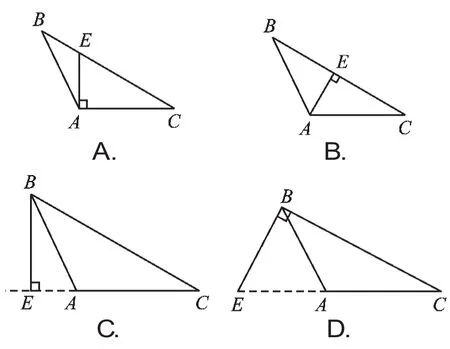
【分析】作哪一条边上的高，从所对的顶点向这条边或这条边的延长线作垂线段即可.故而，在△ABC中，画出边AC上的高，即是过点B作AC边的垂线段，正确的是C.故选C.

【点评】此题主要考查了三角形的高，要抓住定义“在三角形中，从一个顶点向它的对边作垂线，顶点与垂足之间的线段叫作三角形的高”.

重点5：多边形的外角和与内角和

这一部分内容包含：三角形的内角和定理，n边形的内角和公式，多边形的外角和定理.其中，三角形的内角和定理是基础和出发点.

在小学，我们就已经知晓“三角形的内角和为180°”这个结论.到了初中，同学们还需要掌握这个结论的证明方法.这个定理的证明方法有多种，以下仅举出其中一种：

如图7所示，在△ABC中，过A引l∥BC.

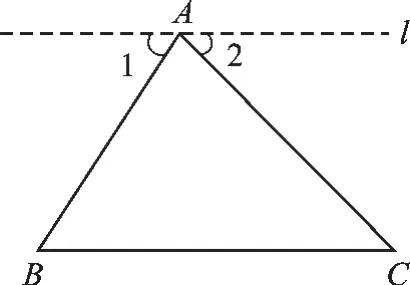
图7

∵l∥BC，

∴∠B=∠1，∠C=∠2（两直线平行，内错角相等）.

∵∠1+∠BAC+∠2=180°，

∴∠A+∠B+∠C=180°.

即三角形的内角和为180°.

由三角形的内角和定理还直接得出以下结论：①直角三角形两锐角互余，②三角形的一个外角等于与它不相邻的两个内角的和.对n边形适当分割，使其转化为若干个三角形，还可以得出n边形内角和公式（n-2）·180°，并最终得出n边形外角和为360°.

例5认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题.

探究一：如图8，在△ABC中，已知O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+∠A，理由如下：

∵BO和CO分别是∠ABC和∠ACB的角平分线，

∴∠BOC=180°-（∠1+∠2）=180°-（90° -∠A）=90°+∠A.

图8

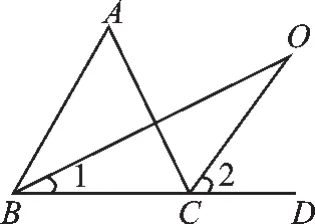
图9

（1）探究2：如图9中，已知O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？并说明理由.

（2）探究3：如图10，已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（直接写出结论）结论：_________.

图10

图11

（3）拓展：如图11，在四边形ABCD中，已知O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？（直接写出结论）结论：__________.

（2）根据三角形的外角性质以及角平分线的定义表示出∠OBC和∠OCB，再根据三角形的内角和定理解答；

（3）同（1）的求解思路.

具体解法如下：

理由如下：∵BO和CO分别是∠ABC和∠ACD的角平分线，

∵∠2是△BOC的一个外角，

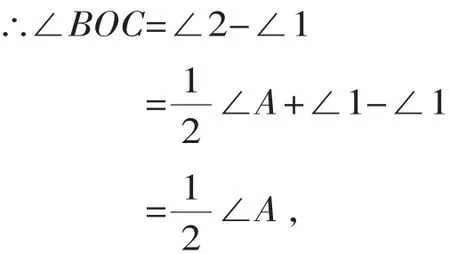
（2）根据三角形的外角性质和角平分线的定义，

在△BOC中，

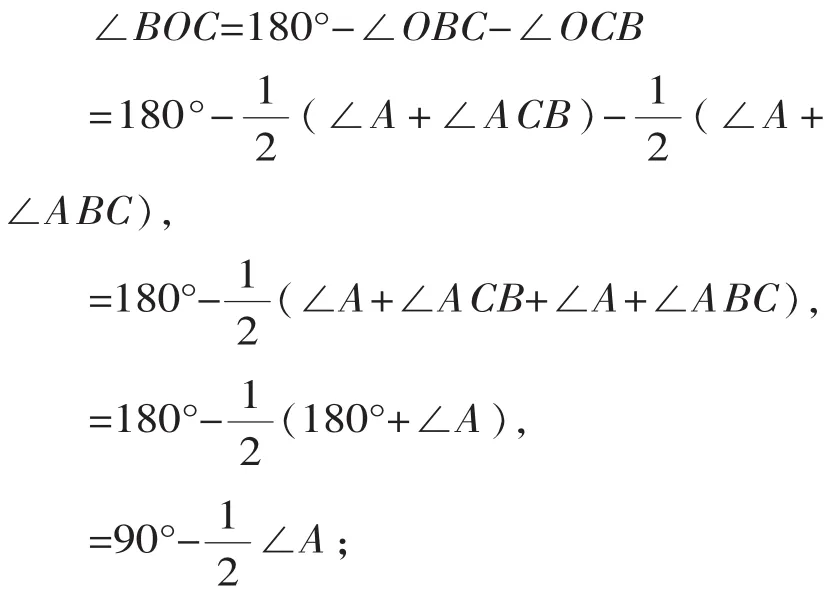
在△BOC中，

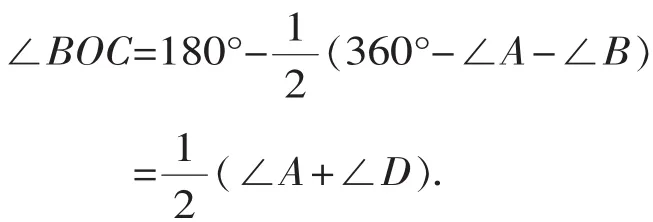
【点评】本题考查了三角形的外角性质、角平分线的定义、三角形的内角和定理，熟记性质并准确识图、整体思想的利用是解题的关键.本题的四个图形属于同一个系列，放在一起比较更容易相互联系进行理解.

在几何内容学习的时候，“转化”是常出现的字眼.“转化”是重要的数学思想，我们不断建构新知识的过程，往往也是不断把新知识转化为已学知识的过程.望同学们能领略其中的奥妙，学得轻松，学得高效.

（作者单位：江苏省南京师范大学附属中学江宁分校）