基于格子Boltzmann法的管道流模拟二维和三维离散模型的比较

葛钦钦，马新华

(江苏大学 流体机械工程技术研究中心，江苏 镇江 21203)

基于格子Boltzmann法的管道流模拟二维和三维离散模型的比较

葛钦钦，马新华

(江苏大学 流体机械工程技术研究中心，江苏 镇江 21203)

格子Boltzmann方法是近二十年迅速发展起来的一种介观模拟方法。它是由格子气自动机理论演化而来，有别于传统模拟方法，具有宏观上离散，微观上连续的特点。本文着重介绍了格子Boltzmann法控制方程的理论基础，基于LBGK理论的D2Q9和D3Q19离散速度模型边界条件的定义以及算法演变情况。使用MATLAB软件编写程序进行二维和三维的泊肃叶流的数值模拟，对比分析D2Q9和D3Q19离散速度模型在LBGK理论下的边界条件的影响。

格子Boltzmann法；LBGK理论模型，D2Q9离散模型；D3Q19离散模型；MATLAB软件

此篇论文的研究工作是基于格子Boltzmann方法(LBM)开展的。这是一种近二十年快速发展起来的较为年轻的数值方法。它是基于粒子动理论，由格子气自动机(LGA)理论演化而来，在系统一定量的离散格子进行计算，通过对大量格子的统计平均值获得宏观结果。LBM属于介观模拟方法，即可以认为该方法在宏观上是离散，在微观上是连续的。与传统的流体力学计算方法相比，LBM具有显著的优势，因为它具有天生的并行特性，边界条件设置简单，程序易于实现等特点，尤其适用于微尺度流型，多相多组分流型和多孔介质流型等许多传统模拟方法难以胜任的领域。

1 数值算法

1.1 Boltzmann传递方程

Boltzmann传递方程由Boltzmann，Mcnamara and Zanetti三位学者于1988年首先提出。其重要意义是引入统计概念，在宏观现象和微观基础之间建立了桥梁[1]。Boltzmann方程的基本思想是不去研究每个粒子的具体运动状态，而是研究大量粒子处在某一运动状态下的概率，通过统计平均的方法得出系统的宏观参数。波尔兹曼方程的推导是基于以下三个假设条件下的[2]。

(1)粒子相互碰撞时只考虑两体碰撞，即三个或三个以上的粒子同时发生碰撞为小概率事件可忽略不计。

(2)粒子混沌假设。即各个粒子的速度分布是独立的，不依赖于其他粒子。

(3)局部碰撞的动力学行为不受外力的影响。

为了刻画粒子的分布情况，我们引入粒子分布函数f(s,u,t)，其中s(x,y,z)表示空间矢量，u(x,y,z)表示速度适量，t表示某一时刻。粒子的运动加速度表示为a。对于任意粒子在时间间隔dt内，运动变化是主体运动和分子间的相互碰撞综合的结果。数学表达式为[3]：

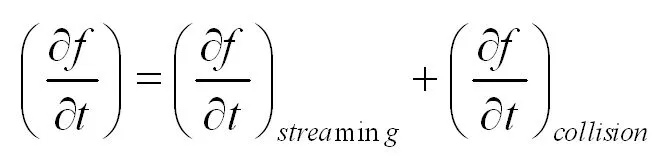
(1)

泰勒展开得：

(2)

根据气体动理论知识对于碰撞项做出数学表达[4]：

(3)

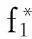
1.2 BGK模型

由方程(3)可知，由于碰撞项的存在，Boltzmann传递方程是一个复杂的微积分方程，给方程的求解带来了很大的困难。所以需要对粒子间的碰撞找出近似合理的简化才能求解方程。

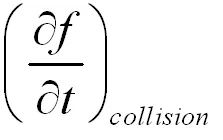
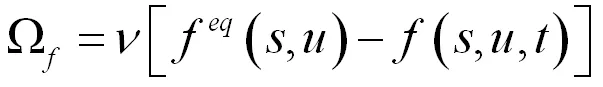
(4)

式中feq(s,u)表示平衡态时的分布函数；比例系数ν和松弛时间τ成反比：

ν=1/τ

(5)

最后我们得到Boltzmann-BGK方程：

(6)

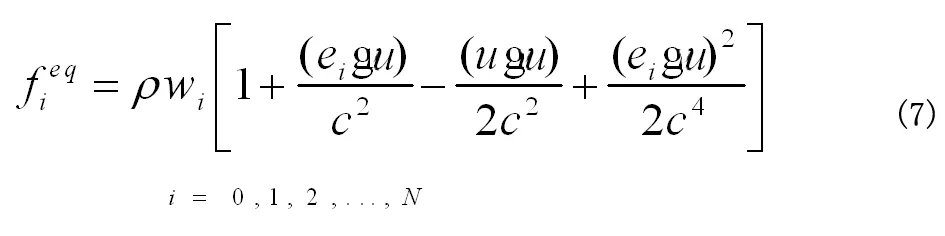
1.3 质量统计与动量统计

单个粒子的分布函数可以简单地认为是代表各个粒子在某一状态下(包括位置矢量和速度矢量)发生的频率。系统的宏观密度和速度可以由系统内所有的粒子分布函数求得[9]。

模型的宏观密度表示如下：

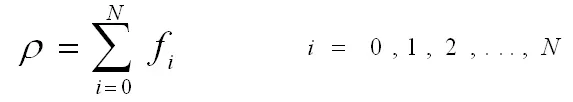
(8)

系统的宏观速度是微观粒子速度矢量和方向密度乘积的平均值，表示如下：

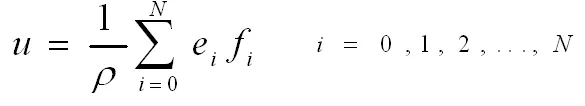
(9)

系统动量的表达式：

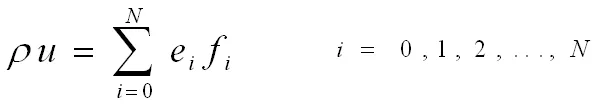
(10)

1.4 LBM二维和三维离散速度模型

90年代初期，Qian等人在LGA理论的FHP离散模型上进行改进，提出DxQy形式(x维空间，y个离散速度)既适合LBM平衡态分布函数又具有完全对称性的系列离散速度模型[10-12]。

其中二维模型中应用最为广泛的是D2Q9模型，图示如下。

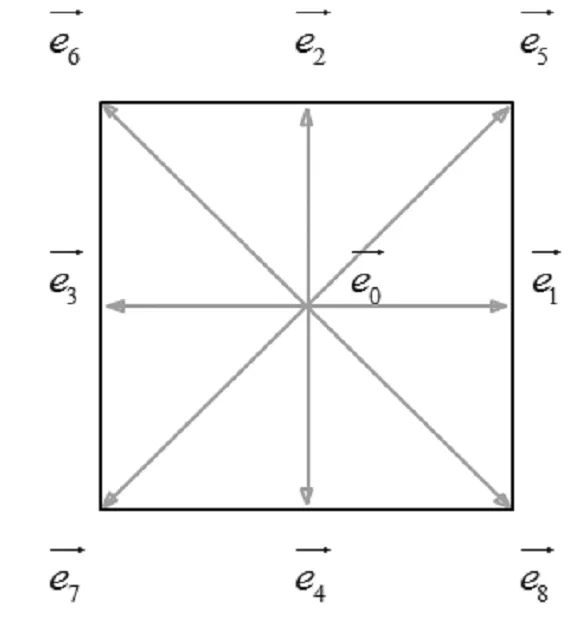
图1 D2Q9离散速度模型

D2Q9速度模型下平衡态分布函数各参数：

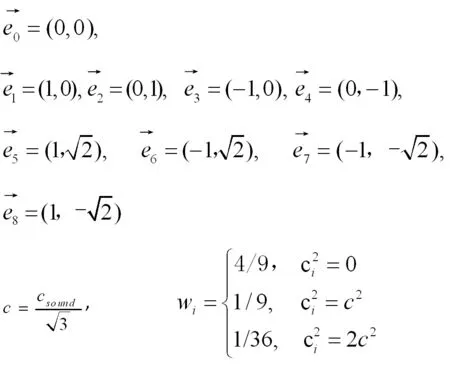
三维模型中应用最为广泛的是D3Q15模型和D3Q19模型，由于D3Q19模型具有更加丰富的离散方向数，所得到模拟结果一般更加精准和可靠。同时更多的离散方向也会给计算提出更高的要求。一般在计算资源充足的条件下，建议采用D3Q19模型。模型给出如下：

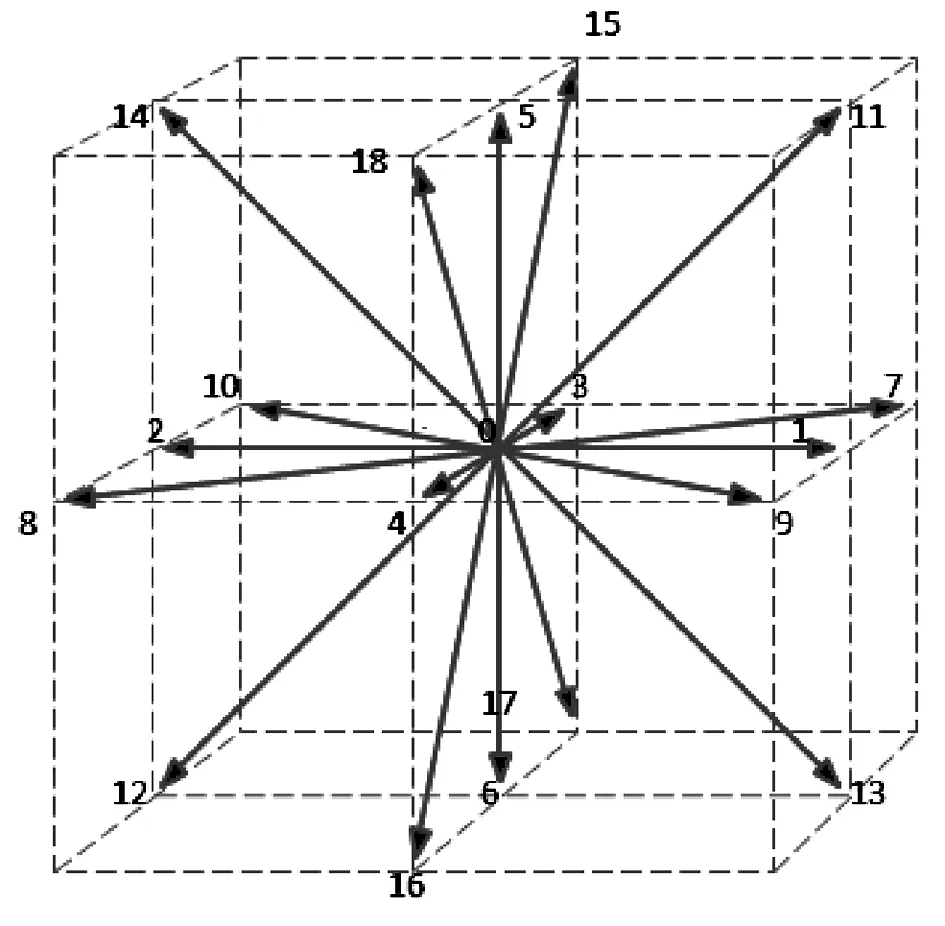
图2 D3Q19离散速度模型

1.5 边界条件

管道流需要处理的边界条件有进出口处和对管壁的边界条件处理。以D2Q9速度模型在管道入口即左边界为例分析LBM边界条件，图示如下：

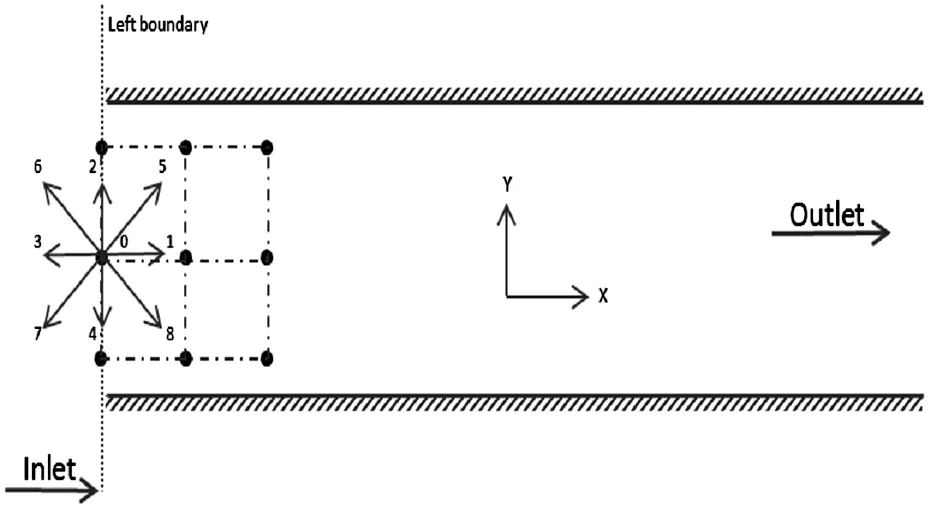
图3 管道进口处的D2Q9边界条件

由方程(8)可知

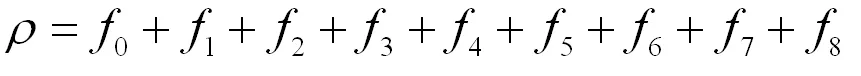
(11)

由方程(11)，对速度矢量u正交分解成ux和uy得出：

(12)

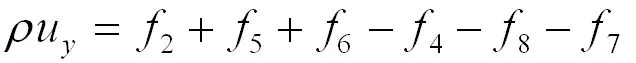
(13)

此时对于左边界情况，未知条件有f1，fs，f8和边界条件处的 ，所以我们需要四个独立方程来求解这四个未知数。现在已有方程(11)，(12)和(13)。Zou -He 边界条件法给出了简化，假设粒子处于非平衡态时钢球反弹规则仍然适用，那么我们则得到了第四个需要的方程[13]：

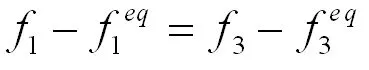
(14)

最终根据以上四个方程求解得出所需的未知边界参数：

对于三维模型D3Q19，我们依然以左边界为例加以说明，未知量有以下六个：p,f1,f7,f9,fu,fb。同二维推到类似，根据方程

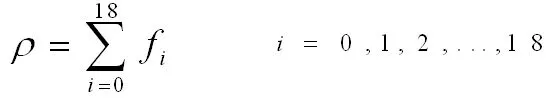
(16)

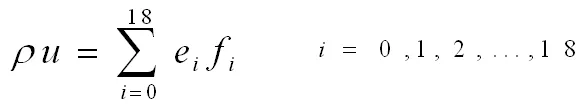
(17)

对速度矢量u正交分解得

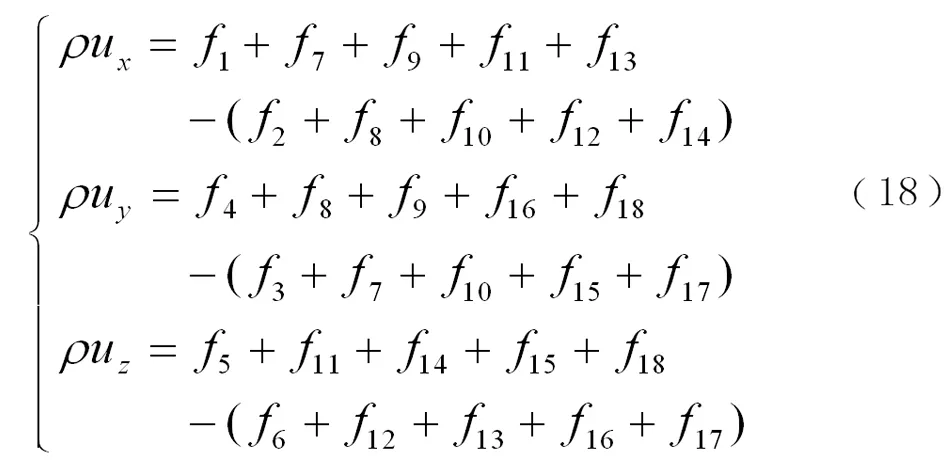
由方程组

ux是进口速度，为已知量。故可求：

在左边界上有Zou -He假设：

(21)

同时满足BGK模型的平衡态分布函数

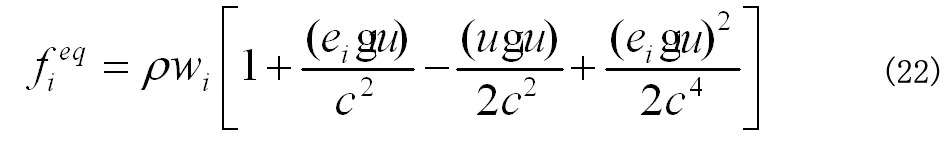
可由以上(21)(22)方程求得

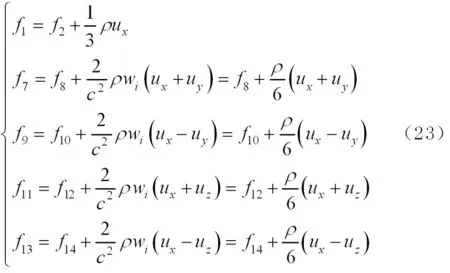
2 两种速度模型的泊肃叶流型的分析对比

2.1 基于Navier-Stokes方程的解析解

设定管道流体的密度为常数，即不可压缩流体。流体流动的驱动力恒定为F。

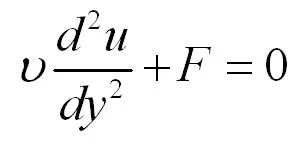
(25)

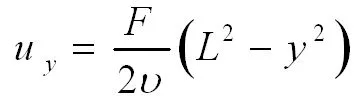
(26)

式中，L为管道的半径，y是计算点处距离管道中心的距离，υ是流体的运动粘度。

2.2 D2Q9数值模拟结果

泊肃叶流是粘性流体在管道中的典型流型，初始条件如图(4)所示：

图4 二维管道泊肃叶流的结构示意图

数值模拟在Matlab软件下进行。流域网格为150*50，雷诺数为100，松弛时间根据松弛系数公式omega = 1/ (3*nu+1/2))得出，其值算出得0.65。进出口边界条件采用Zou-He边界条件，管壁采用刚体反弹边界条件处理。得出模拟结果在平衡态下结果如图(5)所示：

图5 二维管道泊肃叶流平衡态呈现

与解析解结果对比如图(6)所示：

图6 泊肃叶流解析解与D2Q9模拟结果的对比

可以看出LBM理论的数值模拟结果基本吻合解析解的结果。我们通过计算相对误差发现系统的最大误差出现在靠近管壁处。

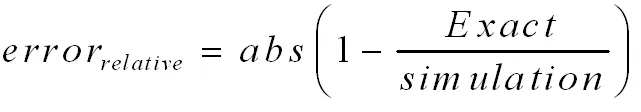
(27)

管道各位置的相对误差如图(7)所示

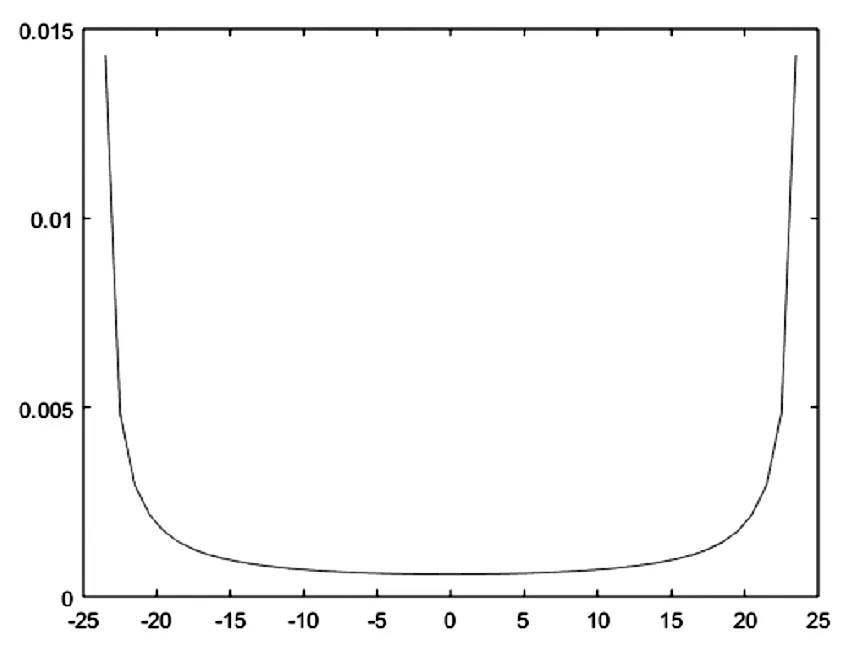
图7 管道各位置解析解与模拟结果的相对误差

这说明对于管壁的边界条件处理我们用的最为理想的刚体弹性方法并不能很精确的反应真实的边界情况。但是优点是可以更加清晰简便的描述问题，减小计算负担。

2.3 D2Q9模型下的质量守恒和能量守恒验算

为了检验LBM算法的稳定性，在管道的进出口处进行质量守恒和能量守恒的验算。进出口的质量和能量计算如方程(28)和(29)

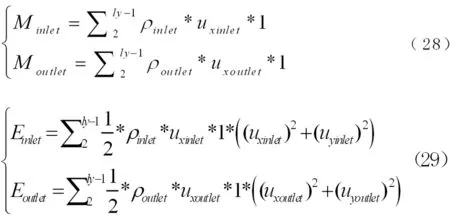
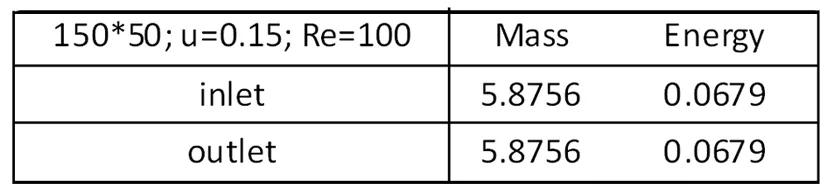
取在不同的进口速度，雷诺数下的计算结果汇总如表格。

150*50;u=0.1;Re=50MassEnergyinlet4.40990.0287outlet4.40990.0287

数值模拟结果表明LBM理论采用D2Q9速度模型，有着很好的稳定性和精确度。

2.4 D3Q19数值模拟结果

结构示意如图所示：

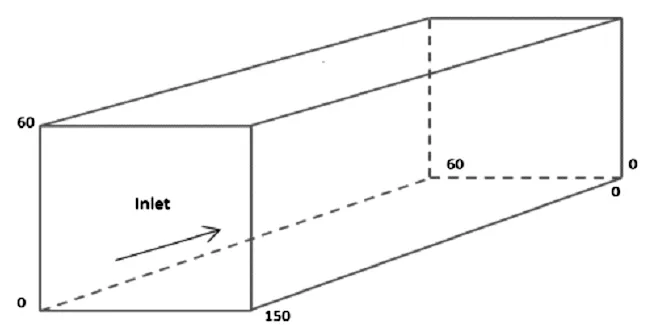
图8 三维管道泊肃叶流的结构示意图

三维管道泊肃叶流采用D3Q19模型进行计算，结。初始条件，在管道进口处给一个水平速度( ， )，雷诺数为100，松弛时间设定为1。进出口边界条件采用引入修正变量的Zou-He边界条件，管壁采用刚体反弹边界条件处理。得出模拟结果在平衡态下结果分别在Y-Z, X-Z 和 X-Y界面进行切片，图示如下：

图9 管道进口，中心和出口处在Y-Z切面上的速度分布

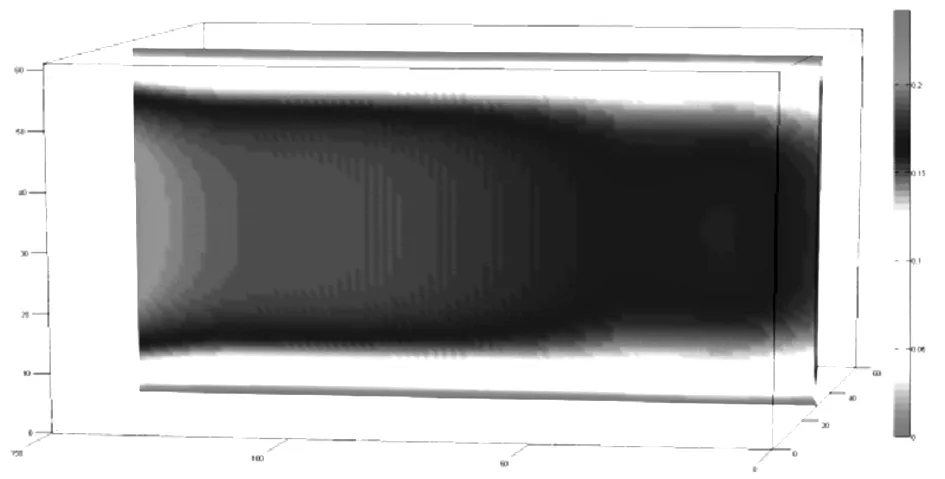
图10 沿Y轴中心的X-Z切片上的速度分布

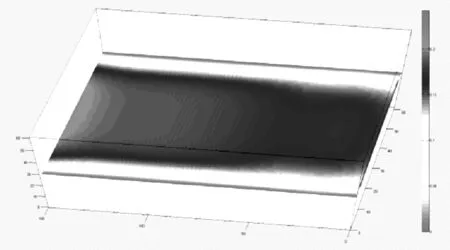
图11 沿Z轴中心的X-Y切片上的速度分布

2.5 D3Q19模型下的稳定性验算

管道横截面为正方形对称结构。根据对称性原理，在算法稳定的情况下，在对应点上X-Y和X-Z切面的上对应点的速度值也应该相等[16]。我们截取管道在出口中心处的X-Y和X-Z切面上的速度分布进行匹配。同时把该案例用D2Q9速度模型进行模拟，与三维结果进行比照。图示如下：

通过对比图像，我们发现在D3Q9速度模型下，出口处的X-Y和X-Z切面的上的速度能够很好的匹配，表明LBGK模型用D3Q19速度模型下的算法是稳定可靠的。同时与在二维的模拟中出口处所得到的速度分布进行对比，我们发现所得到的速度分布趋势大致相同，特别是在流域中心处更为接近。但是D3Q19模型出口处各点的速度分布均略大于使用D2Q9模型下的速度。根据流体力学知识，靠近管壁处的层流内层速度梯度无限小接近于0，二维的模拟结果很好的符合这一特性，而三维的模拟结果靠近管壁处速度虽然很小但是没有达到0。分析三维数值模拟出现偏差的原因可能是管壁边界条件假设的过于理想化。无滑移刚体反弹的边界条件是使用最为广泛的，原因是把边界条件做出理想化假设达到简化的效果，从而易于实现和理解。在二维的模拟中可以做出定性的分析能保证一定的正确性。但是在三维较为复杂的情况下就会与真实情况出现偏差。

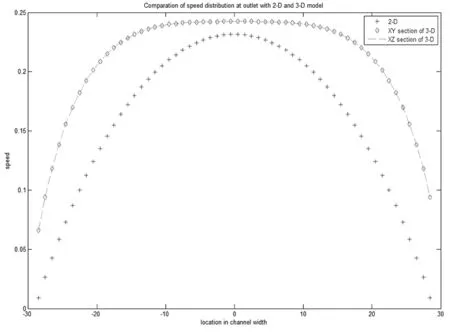
图12 泊肃叶流在二维和三维速度模型下的结果对比

[1] A A. Lattice Boltzmann method fundamentals and fngineering applications with computer codes[M]. London: Springer London Dordrecht Heidelberg New York Springer-Verlag London Limited,2011.

[2] 何雅玲,李 庆,王 勇,等. 格子Boltzmann方法的工程热物理应用[J]. 科学通报,2009,18:2638-2656.

[3] Sauro Succi. The lattice Boltzmann equation, for fluid dynamics and beyond[M]. Oxford ：Oxford Science Publications,2001.

[4] Chen S, Doolen G D. Lattice Boltzmann method for two phase flow modeling[J]. Annual Review of Fluid Mechanics, 1998, 30: 329-364.

[5] Wolf-Gladrow Dieter A. Lattice-gas cellular automata and lattice Boltzmann models:an introduction[M]. [S.I.]:Spring,2000.

[6] 王 亮. 基于格子Boltzmann方法的非常规颗粒两相流的机理研究[D].武汉：华中科技大学,2012.

[7] 胡安杰. 多相流动格子Boltzmann方法研究[D].重庆大学,2015.

[8] He X，Chen S, Doolen G D. A novel thermal model for the Lattice Boltzmann method in incompressible limit[J]. Journal of Computational Physics, 1998, 146(1):282-300.

[9] Peng Y, Shu C, Chew Y T. Simplified thermal lattice Boltzmann model for incompressible thermal flows[J]. Physical Review E,2003, 68(2): 026701-026709.

[10] Aidun C K. Lattice-Boltzmann method for complex flows[J]. Annual Review of Fluid Mechanics, 2009, 42(1):439-472.

[11] He X, Luo L S. Lattice Boltzmann model for the incompressible navier-stokes equation[J].Journal of Statistical Physics, 1997,88:927-944.

[12] 邓平平. 基于格子Boltzmann方法的二维多孔介质渗流研究[D].大连理工大学,2014.

[13] 陈 柔. 格子Boltzmann方法的若干应用[D].杭州：浙江师范大学,2013.

[14] ames Maxwell Buick.Lattice Boltzmann methods in interfacial wave modelling[D]. Edinburgh: University of Edinburgh,1997.

[15] 李 元. 格子Boltzmann方法的应用研究[D].合肥：中国科学技术大学,2009.

[16] 王福军.计算流体动力学分析--CFD软件的理论与应用[M].北京：清华大学出版社，2004.

(本文文献格式：葛钦钦，马新华.基于格子Boltzmann法的管道流模拟二维和三维离散模型的比较[J].山东化工，2016，45(12)：146-150，153.)

2016-04-15

TQ019

A

1008-021X(2016)12-0146-05