基于数值模拟的封隔器胶筒参数正交优化分析

周先军，崔光宇，钟卫平，李英松，边　杰

(1.中国石油大学(华东) 机电工程学院，山东 青岛 266580；2.中海油田服务股份有限公司 完井中心，天津 300459)



基于数值模拟的封隔器胶筒参数正交优化分析

周先军1，崔光宇1，钟卫平1，李英松2，边杰2

(1.中国石油大学(华东) 机电工程学院，山东 青岛 266580；2.中海油田服务股份有限公司 完井中心，天津 300459)

采用ANSYS有限元分析方法对封隔器的组合胶筒系统进行单因素离散优化，得出了单因素参数对组合胶筒接触应力影响规律和最优取值区间，并结合正交试验理论考虑因素间交互作用，对组合胶筒四因素三水平正交优化。结果表明：四因素三水平优化的最优几何参数组合比单因素最优值的组合更符合目标函数要求。该最优组合使得胶筒与套管峰值接触应力增大了11%，较高水平的接触应力分布区域更长，能够取得更好的密封效果。

封隔器；双胶筒；有限元；接触应力；正交优化

封隔器作为油田分层工艺的重要井下工具，被广泛使用在完井、注水、压裂、酸化、防砂、机械采油、气举等采油工艺技术中。封隔器胶筒(以下简称胶筒)的密封性能对于整个封隔器安全可靠密封有着决定性作用[1]。合理设计胶筒形状和几何参数可大幅提高胶筒系统密封性能，封隔器的密封性能可以通过胶筒与套管间的峰值接触应力来评价，该应力应不低于压差，并且在胶筒不出现“肩突”失稳的情况下，峰值接触压力越大，胶筒系统所能承受的密封压差越大[2-4]。

本文基于非线性、超弹性及大变形的有限元分析技术，采用两参数Mooney-Rivlin本构模型，考虑胶筒与套管、隔环和中心管之间的摩擦接触等因素，对某厂的177.8 mm(7 英寸)过电缆封隔器压缩式双胶筒进行研究，数值模拟胶筒几何参数对密封性能的影响，并结合正交试验理论开展胶筒几何参数优化设计。

1　胶筒系统优化模型建立

1.1优化模型建立

以某封隔器中丁腈橡胶的双胶筒系统为研究对象，忽略局部放气孔对密封性能的影响，建立胶筒系统平面优化分析模型，胶筒的几何参数如图1所示。

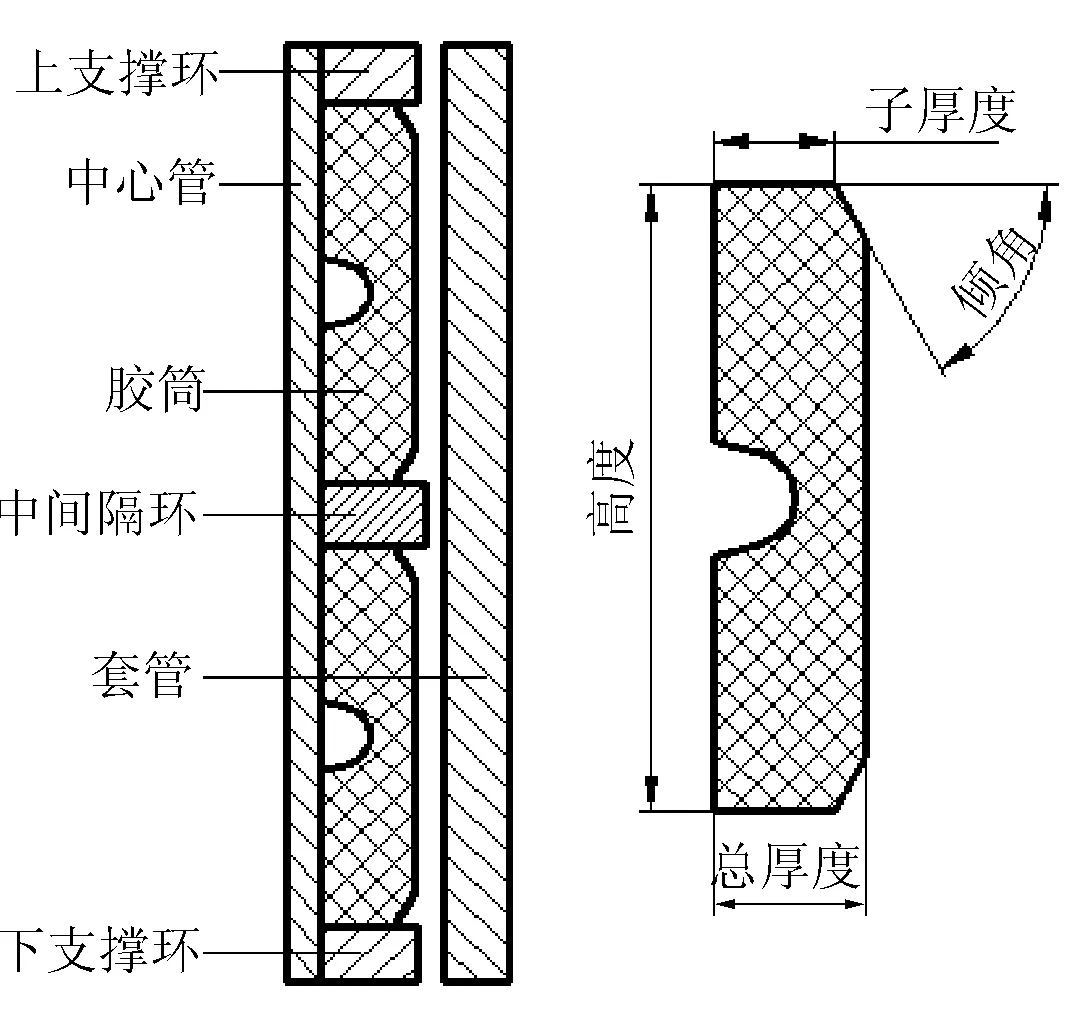
图1　组合胶筒系统模型及几何参数

1.2材料参数

过电缆封隔器胶筒选用的材料是丁腈橡胶，硬度82 IRHD，橡胶硬度Hr(IRHD硬度)与弹性模量E0的关系[5]：

logE0=0.019 8Hr-0.543 2

采用2参数的Mooney-Rivlin橡胶材料模型，该理论基于橡胶是不可压缩的，而且在变形前是各向同性的假设。在两参数Mooney-Rivlin模型中：

E0=6(c10+c01)

由经验公式计算得出，常温下82 IRHD硬度丁腈橡胶的Mooney-Rivlin模型常数c10为1.337，c01为0.668。

1.3边界条件及载荷

胶筒与套管、隔环和中心管之间建立刚柔接触，胶筒为柔性面，套管、隔环和中心管为刚性面，摩擦因数为0.3，胶筒采用Plane182超弹单元，套管、中心管以及隔环等用PLANE42平面单元。中心管和套管上下端施加y方向约束，考虑套管外水泥胶结作用，在套管外侧施加x方向约束；上支撑环上端施加32 MPa面载荷模拟轴向载荷[6]。

2　组合胶筒单因素优化

以胶筒系统峰值接触应力作为其优化目标函数，采用离散优化方法进行一维优化设计，研究子厚度、总厚度、高度及倾角对峰值接触应力的影响，并优选参数。

2.1胶筒子厚度对组合胶筒密封性能的影响

对组合胶筒子厚度开展单因素离散优化，压缩距及力学性能变化趋势如图2所示。随着子厚度增加，压缩距整体呈现减小的趋势，接触应力大小波动变化，存在最优子厚度，其中最优的子厚度为8.5 mm。

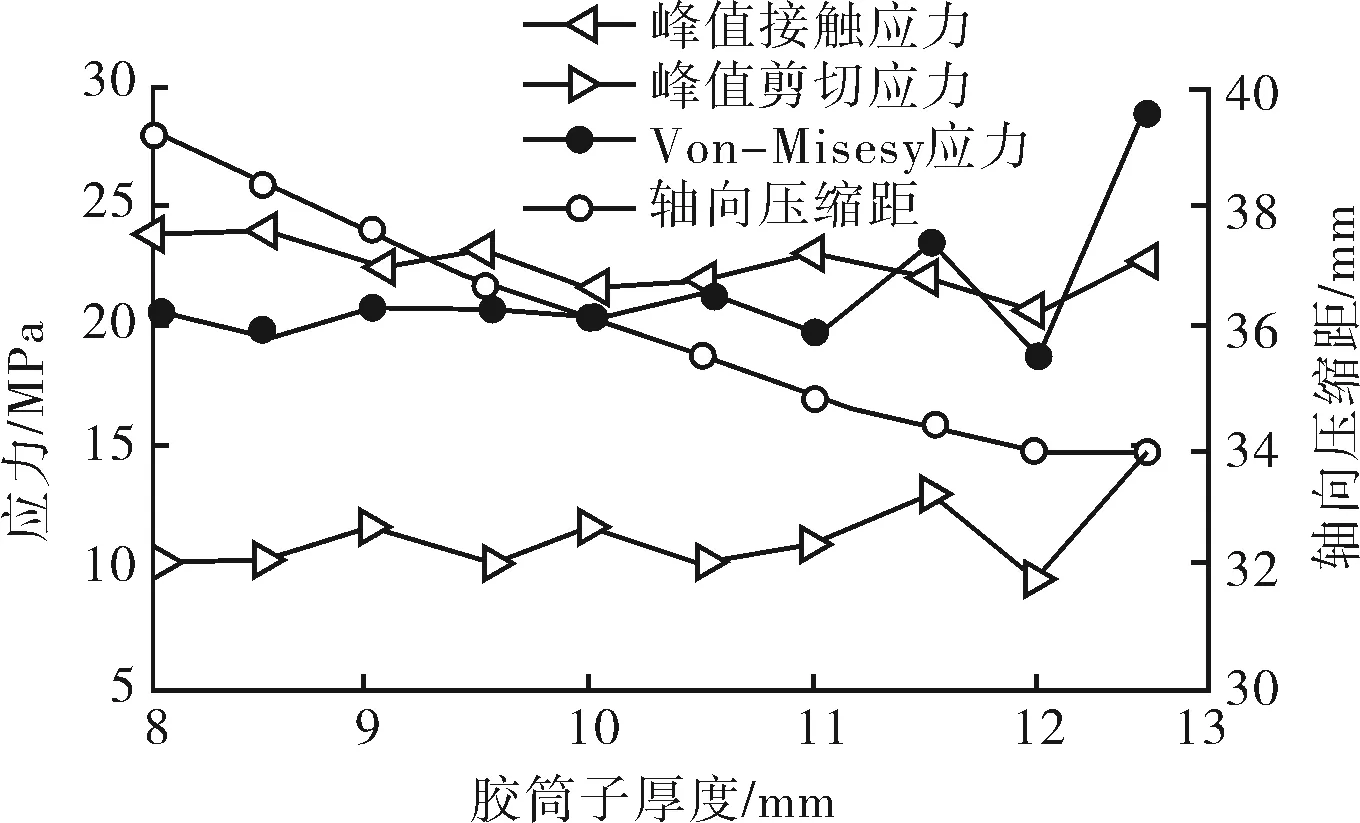
图2　组合胶筒子厚度离散优化

子厚度过大，应力急剧增大，可能导致胶筒撕裂破坏，如果子厚度由12 mm增大为12.5 mm，接触应力增大4.3%，但剪切应力增大了46%，Von-Mises应力增大了36%，造成胶筒发生破坏。

2.2胶筒总厚度对组合胶筒密封性能的影响

在12.5 ～14.0 mm的优化区间，逐次优化胶筒总厚度，结果如图3所示。随着胶筒总厚度的增加，胶筒的压缩距近似呈线性关系减小，对于组合胶筒而言，下胶筒的密封饱满程度受到影响，这不利于整体的密封。

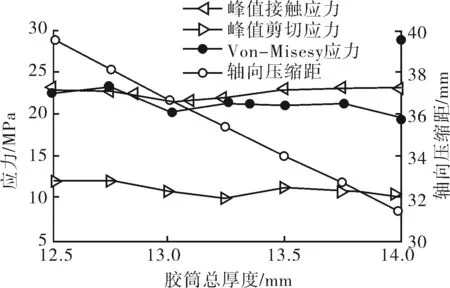
图3　组合胶筒总厚度离散优化

总厚度为13 mm时，峰值接触应力处在波谷，总厚度增加，接触应力呈现增大趋势。总厚度由13.25 mm增大到13.5 mm，接触应力增大将近7%。总厚度继续增加，接触应力都保持在较高水平，且剪切应力和Von-Mises应力均变化不大。因此，在采油工艺允许的条件下，增大总厚度有利于胶筒密封。

2.3胶筒的倾角对组合胶筒密封性能的影响

增大倾角容易坐封，但倾角过大会导致应力集中，胶筒变形过大而引起密封元件损坏，解封困难，而倾角较小时，在压力不是很大的情况下就会发生肩突，引起胶筒撕裂失效[7-11]，故选定倾角优化区域为30～63°，倾角对胶筒密封性能的影响如图4所示。

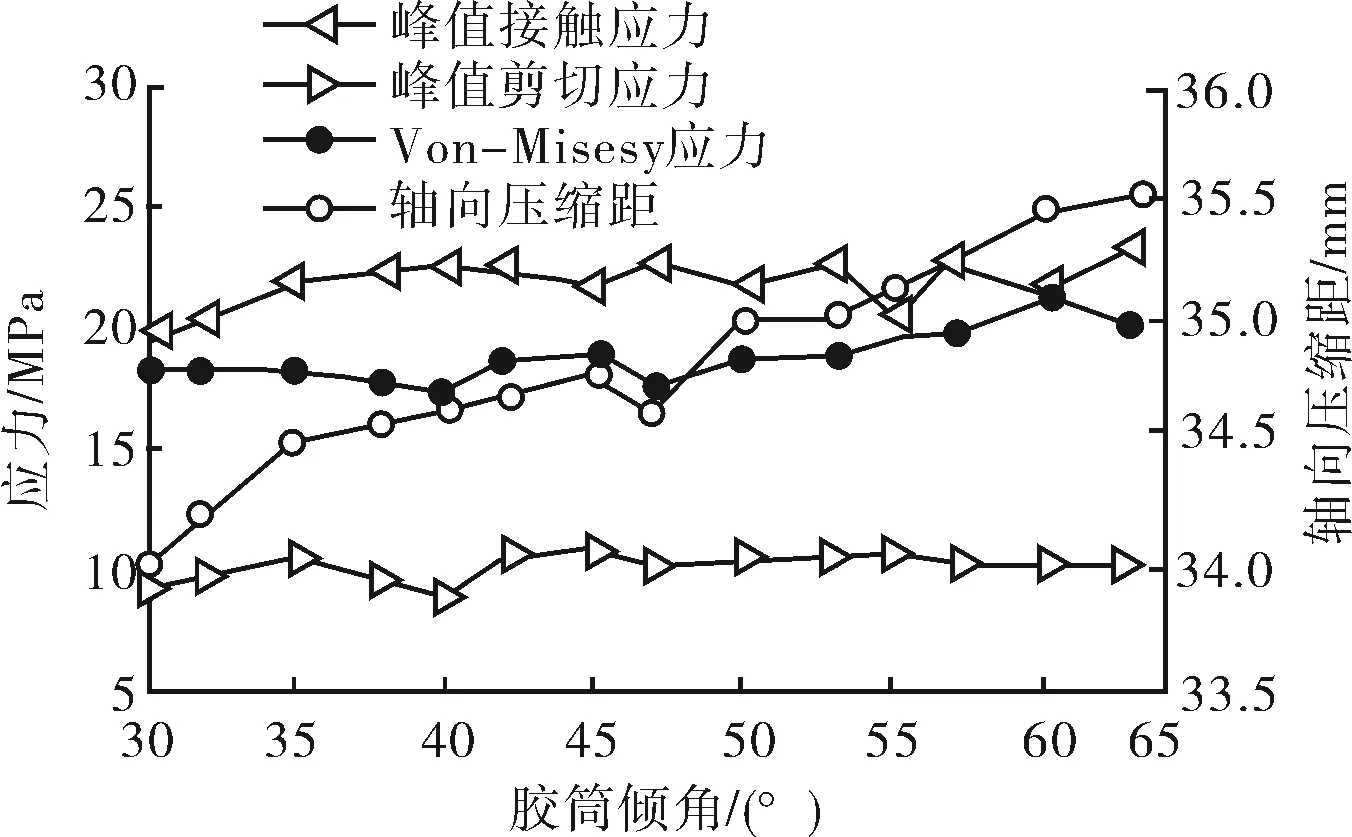
图4　组合胶筒倾角离散优化

胶筒倾角增加，胶筒的轴向压缩量是缓慢增大的，在小于45°时，接触应力随着倾角增大而增大，40°附近接触应力有个小峰值，且剪切应力和Von-Mises应力都处于波谷，认为该值对应的胶筒力学性能较为理想，随后倾角增大，接触应力波动变化，在47°、53°和63°，接触应力均处于较高值。

2.4胶筒的高度对组合胶筒密封性能的影响

高度在42～70 mm，离散计算胶筒高度对接触应力及力学性能的影响，如图5所示。胶筒高度增加，压缩距近似呈线性增大，剪切应力逐步减小，Von-Mises应力变化不大。

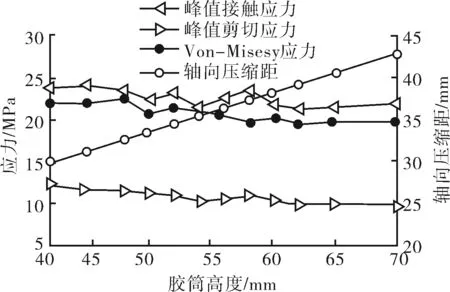
图5　组合胶筒高度离散优化

在高度小于50 mm的区间，高度减小，接触应力整体增大，但胶筒两端受到的剪切应力也增大，容易造成剪切破坏，导致其能承受的坐封压力较小；高度在50 ～58 mm，高度增加，其接触应力波动较大。高度超过58 mm，增加胶筒高度，接触应力逐渐减小，且胶筒高度过大时容易引起失稳。

3　组合胶筒四因素三水平优化

基于组合胶筒单因素优化结果，考虑组合胶筒是受多结构参数的共同影响，四因素三水平全部组合数量为81种，从效率方面考虑，运用正交试验理论，正交参数化优化设计的组合数为27次，可大幅提高效率。

3.1正交优化设计因素及水平数选定

组合胶筒子厚度、总厚度、倾角和高度等是影响密封性能的主要因素，基于单因素优化分析结果，其因素水平表如1所示。

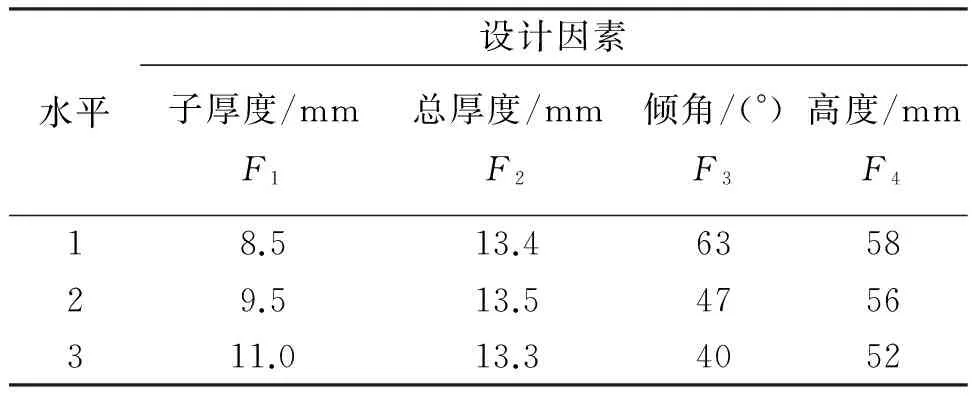
表1　正交因素水平表

3.2正交表及表头设计选用

考虑子厚度和总厚度、倾角、高度的交互影响，四因素三水平正交优化选用L27(313)正交表，设计表头如表2所示。

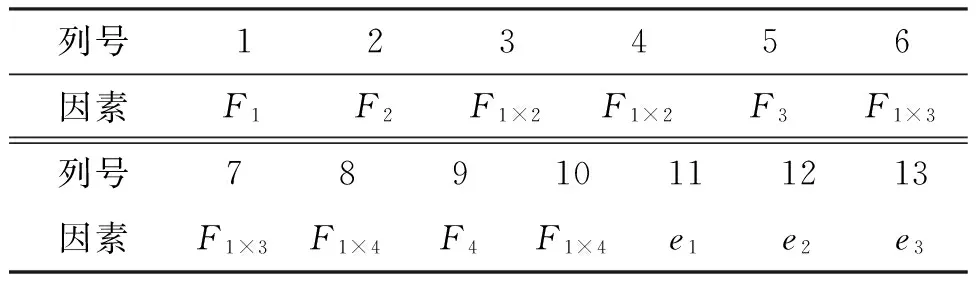
表2　正交优化表头

3.3极差分析与方差分析

3.3.1极差分析

1)不考虑交互作用的最佳组合是(2，2，3，1)，即子厚度为9.5 mm，总厚度为13.5 mm，倾角为40°，高度为58 mm，求解得其接触应力为22.31 MPa。

2)各因素对胶筒与套管峰值接触应力(目标函数)的影响顺序是：高度>总厚度>倾角>子厚度。

3.3.2方差分析

查询F-分布表，计算各因素及交互作用的F比，比较判断后，发现各个因素及交互作用都不显著，这是由于结果的波动范围比较小，在27次优化设计中，接触应力在21.06～24.09 MPa波动变化。4个因素共有81种组合，因素间有交互作用，通过[12]：

⋮

计算出这81种组合的值，并得出最优组合为(3，2，1，1)。该组合对应胶筒参数为子厚度11 mm，总厚度13.5 mm，倾角63°，高度58 mm。该结构胶筒的峰值接触应力为24.09 MPa，相比不考虑交互作用分析结果，更满足目标函数要求，即峰值接触应力更大，优化前后性能对比如表3所示。

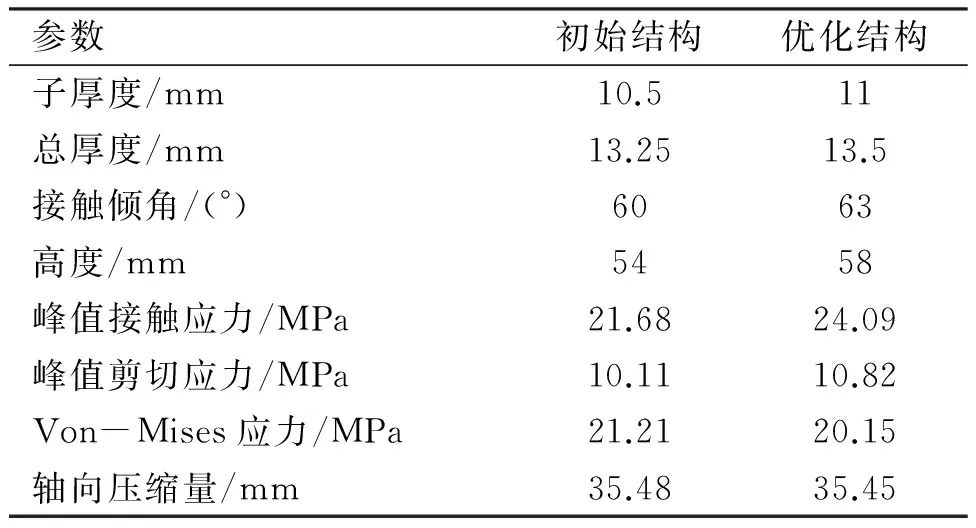
表3　优化前后结构参数与力学性能对比

优化后胶筒密封结构的压缩距基本不变，剪切应力略有增大，但Von-Mises应力较优化前有所减小，且优化后结构的峰值接触应力增大11%，沿胶筒轴向，优化后结构的较高水平的接触应力分布区域更长，如图6所示，故优化后的胶筒结构能够取得较好的密封效果。

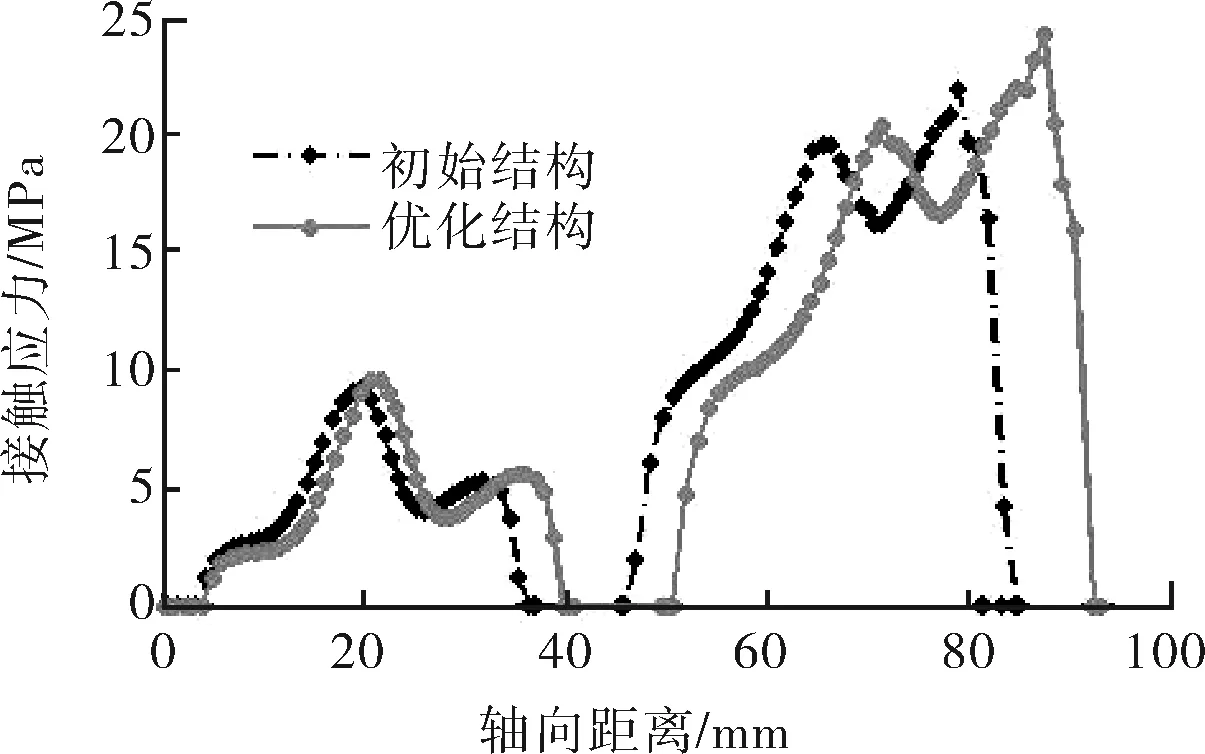
图6　优化前后组合胶筒接触应力分布

4　结论

1)对于该型号组合压缩式双胶筒系统，单因素分析结果表明：胶筒子厚度在8.5～11.0 mm较优，总厚度在工艺许可条件下应尽可能增大，倾角在40～60°较优，高度在50～60 mm较优。

2)考虑交互作用，该型号组合胶筒系统的四因素三水平正交优化得出结构最优参数为子厚度11 mm，总厚度13.5 mm，倾角63°，高度58 mm。

3)胶筒优化后，胶筒与套管峰值接触应力达到24.09 MPa，增大11%，且较高水平的接触应力分布区域更长，能够取得更好的密封效果。

[1]Rune Freyer，ArveHuse.Swelling Packer for Zonal Isolation in Open Hole Screen Completions[G].SPE，78312，2002：29-31.

[2]张辛，徐兴平，王雷.封隔器胶筒结构改进及优势分析[J].石油矿场机械，2013，42(1)：62-66.

[3]周先军，平利，季公明.封隔器胶筒接触应力分布有限元计算[J].钻采工艺，2002，25(4)：51-52.

[4]伍开松，朱铁军，侯万勇，等.胶筒系统接触有限元优化设计[J].西南石油学院学报，2006，28(6)：88-90.

[5]郑明军，谢基龙.压缩状态下橡胶件大变形有限元分析[J].北方交通大学学报，2001，25(1)：76-79.

[6]杨秀娟，杨恒林.液压封隔器胶筒座封过程数值分析[J].石油大学学报(自然科学版)，2003(5)：84-87.

[7]刘永辉，付建红，林元华，等.封隔器胶筒结构参数优化分析[J].机械工程师，2007，38(7)：66-67.

[8]赵政璋，王元基，隋军，等.油田注水开发技术与管理[M].北京：石油工业出版社，2010.

[9]于九政，陈伟，晏耿成，等.多级分注井封隔器研制与应用[J].石油矿场机械，2012，41(11)：66-68.

[10]张丽娟，赵广民，赵粉霞，等.Y241型封隔器分压管柱可靠性分析[J].石油矿场机械，2010，39(7)：25-28.

[11]赵朋宸.分层注水管柱封隔器受力分析[J].长江大学学报：自然科学版，2011，8(4)：59-62.

[12]刘振学.实验设计与数据处理[M].北京：化学工业出版社，2005.

Orthogonal Optimization Analysis of Packer Rubber Parameters by Numerical Simulation

ZHOU Xianjun1，CUI Guangyu1，ZHONG Weiping1，LI Yingsong2，BIAN Jie2

(1.College of Mechanical and Electrical Engineering，China University of Petroleum，Qingdao 266580，China；2.Well Completion Center，China Oilfield Services Ltd.，Tianjin 300459，China)

The single factor for discrete optimization study is taken in this paper and the influence on contact stress and the optimal area of rubber single geometric parameters were obtained based on ANSYS numerical analysis.Considering the interaction of factors，four factors and three levels orthogonal optimization analysis were done combined with orthogonal test.The results showed that the optimal combination of geometric parameters of four factors and three levels orthogonal optimization is more in line with the requirements of the objective function compared with combination of univariate optimal value.The peak contact stress between rubber and casing was increased by 11% and longer distribution of higher contact stress was obtained result in better sealing effect.

packer；rubber；finite element；contact stress；orthogonal optimization

1001-3482(2016)05-0060-04

2015-11-17

周先军(1971-)，男，山东淄博人，副教授，博士，研究方向为石油机械以及静密封等，E-mail：zxjqhy@126.com。

TE931.202

A

10.3969/j.issn.1001-3482.2016.05.013