一种改进的A*算法在电缆敷设设计中的应用

杨亚伟，王　璐， 王　斐（.山东电力工程咨询院有限公司，山东济南5003；.山东省质量技术监督教育培训中心，山东济南5003）

一种改进的A*算法在电缆敷设设计中的应用

杨亚伟1，王璐2， 王斐1
（1.山东电力工程咨询院有限公司，山东济南250013；2.山东省质量技术监督教育培训中心，山东济南250013）

针对常规A*算法仅以路径最短作为限制条件而无法约束路径弯曲次数的问题，提出一种改进的A*算法，该算法在保证路径最短的前提下，同时考虑路径的弯曲次数问题，最终得到一条弯曲次数最少的最短路径。仿真结果显示，在电缆敷设设计中应用该算法，可以有效降低电缆的总弯曲次数，从而降低电缆敷设的施工难度，提高电缆的可靠性。

A*算法；电缆敷设；电缆弯曲

0　引 言

电缆是发电厂中一个非常重要的组成部分，它就像整个发电厂的血管与神经系统一样，遍布厂区各个角落，其可靠性直接决定了整个发电厂的可靠性和安全性。造成电缆出现故障的原因有很多，其中电缆的弯曲半径过小，是一个比较常见的原因［1］。

在电缆敷设施工时，如果对电缆过度弯曲，导致电缆的弯曲半径过小，则有可能会对电缆的绝缘性能造成影响，从而在运行过程中引起短路、击穿等故障［2］。虽然相关规程中对电缆的弯曲半径都有明确的限制，但是由于在施工过程中执行不严格，检查不到位，电缆弯曲半径过小的问题仍然普遍存在［3］。

近年来，随着机组容量的不断增加，发电厂中电缆的数量也变得越来越多，因此利用计算机辅助电缆敷设软件来预先进行电缆敷设的设计工作，已经成为近年来一种常见的设计手段［4］。由于发电厂中电缆桥架及电缆沟的布置较为复杂，某些电缆的起点与终点之间往往存在多条等长的电缆路径。因此，在进行电缆敷设的设计时，在保证电缆路径最短的前提下，如果能尽可能减少电缆的弯曲次数，不仅可以减少现场施工的工作量，同时也能够降低电缆因为弯曲半径过小而出现故障的概率。

1　等长路径下电缆的弯曲次数问题

为了说明等长路径下电缆的弯曲次数问题，我们给出一个简化的电缆敷设模型如图1所示。

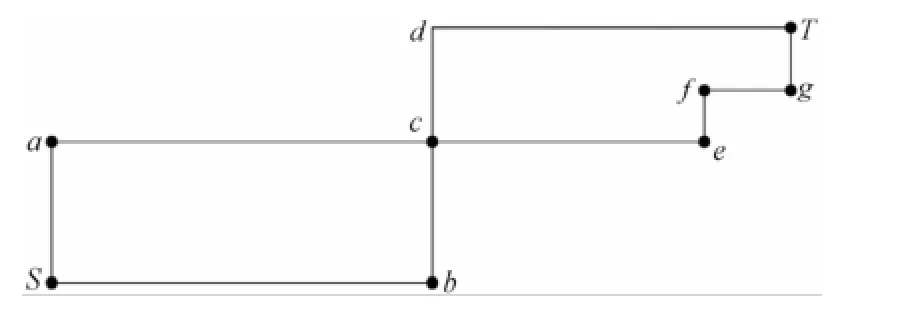
图1　电缆敷设模型

在图1所示的电缆敷设模型中，假设电缆的起点为S，终点为T，通过观察我们可以发现，在起点S和终点T之间，共有4种不同的敷设路径，并且这4种敷设路径是等长的，分别统计这四种敷设路径的电缆弯曲次数，结果如表1所示。

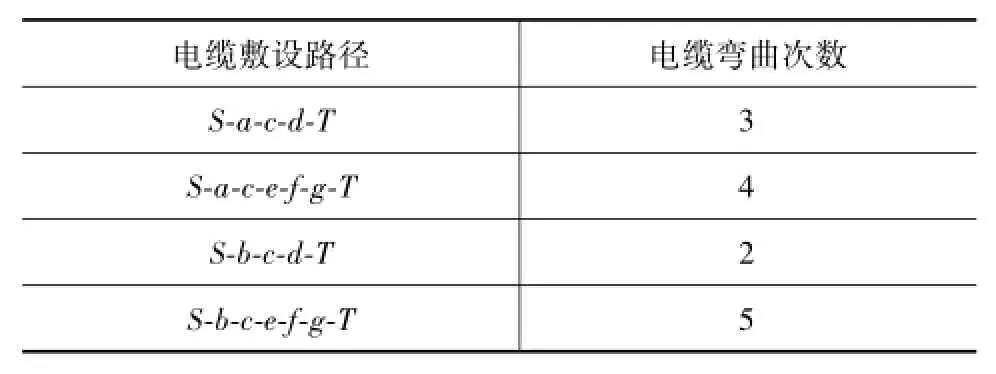
表1　敷设结果

从表1可以发现，虽然四种敷设路径具有相同的敷设长度，但是其电缆的弯曲次数却相差很多。如果仅仅以路径最短作为电缆敷设的唯一标准，那么表1中的四种敷设路径均可以作为最优结果。但如果从实际施工的角度来考虑，在保证路径最短的前提下，应尽量选择电缆弯曲次数最少的那条敷设路径，以便降低现场施工难度，同时也有利于提高电缆的稳定性和可靠性。

2　常规A*算法及其不足之处

计算机辅助电缆敷设软件的主要工作是为每一根电缆寻找一条最优的敷设路径，因此路径搜索算法便成为计算机辅助电缆敷设软件的核心算法。目前较为成熟的路径搜索算法主要有解析算法和启发式算法两种，分别以Dijastra算法和A*算法为典型代表，其中A*算法由于在计算速度和规模上具有一定优势［5］，因此在电缆敷设软件中得到了广泛的应用。

2.1 A*算法的基本思想

A*算法是一种典型的启发式路径搜索算法，其核心思想是估价函数的设计［6］。在选择当前节点的下一个搜索节点时，引入了估价函数f（n）

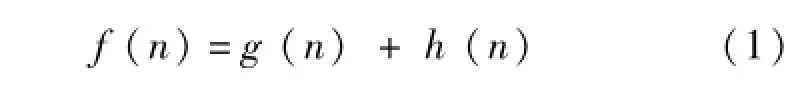
式中：n为待扩展的节点；f（n）为从起始节点到节点n的一条最佳路径的实际代价加上从节点n到目标节点的一条最佳路径的代价之和；g（n）为从起始节点到节点n之间的最短路径的实际代价；h（n）为从节点n到目标节点的路径估计代价。

A*算法就是在每次选取节点时，从所有候选节点中选择f（n）值最小的那个节点进行扩展。A*算法的流程图如图2所示。

2.2 常规A*算法的不足之处

常规A*算法以路径最短作为衡量结果优劣的唯一标准，当起点与终点间存在多条等长的最短路径时，常规A*算法会随机选取其中一条路径作为最终结果，而舍弃其它等长的结果。在仅考虑路径长度这一个因素时，这种处理方式没有任何问题，但是如果想要在路径最短的前提下，尽可能降低电缆的弯曲次数，那么常规A*算法此时已经不能满足我们的要求。

在对A*算法进行改进之前，首先来分析一下造成上述不足之处的原因。我们以图1所示的电缆敷设模型为例，根据图2所示的流程图，得到常规A*算法的路径搜索过程如表2所示。

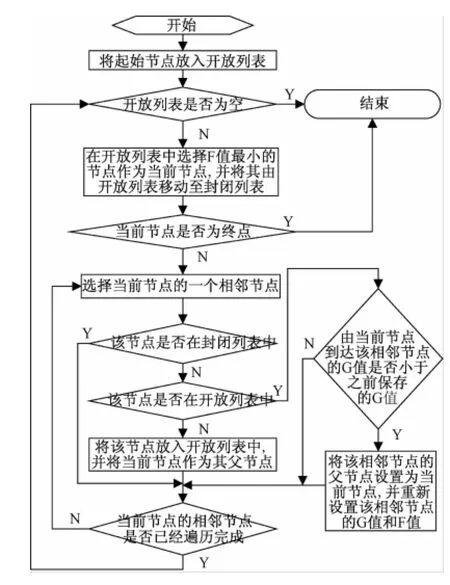
图2　A*算法流程图

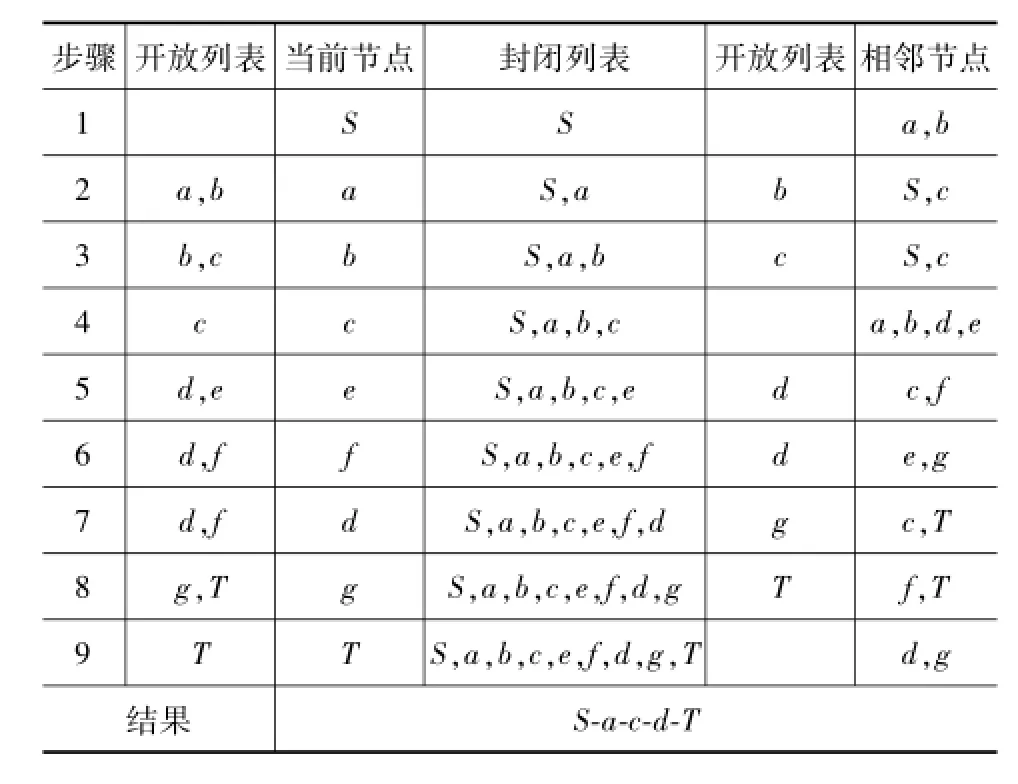
表2　A*算法搜索过程

将表2的搜索结果与表1中的数据进行对比后发现，常规A*算法并没有得到一条弯曲次数最少的结果。与弯曲次数最少的路径S-b-c-d-T相比，上述结果在S-a-c与S-b-c这两条等长路径中错误地选择了前者，造成最终弯曲次数的增加。通过观察表2中的具体搜索过程发现，在搜索过程的第2步，算法发现了由起点S到节点c的路径S-a-c，而在搜索过程的第3步，算法发现了另一条由起点S到节点c的路径S-b-c，由图2所示的算法流程图得知，当在起点与某个节点间存在多条可达路径时，如果后发现的路径长度不小于之前发现的路径长度，则后发现的路径将被舍弃。在上面的搜索过程中，由于从起点S至节点c之间的路径S-a-c先被发现，而后发现的路径S-b-c其长度并不比S-a-c小，因此路径S-a-c被舍弃。

3　改进的A*算法

通过上面的分析过程我们发现，如果想要得到一条弯曲次数最少的最短路径，关键在于当在搜索过程中遇到两条长度相同的路径时，并不能简单地随机选取其中一条路径，而是应该对比这两条路径的电缆弯曲次数，选择弯曲次数较少的那条路径。

需要注意的是，当在搜索过程中，遇到两条长度相同且弯曲次数也相同的路径时，我们并不能简单地认为这两条路径是完全等同的而去随机选取其中一条作为最终结果，原因如下：

假设在起点S与终点T之间，存在一点M，在S与M之间存在多条等长路径，且这些路径具有相同的弯曲次数CSM，则起点S与终点T之间经过点M的路径弯曲次数可以表示为

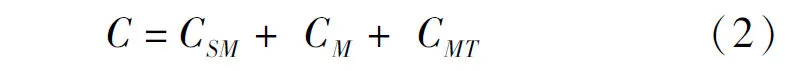
式中：C为整条路径的弯曲次数；CSM为起点S与中间点M之间路径的弯曲次数；CM为该路径在点M处的弯曲次数（取值为0或1）；CMT为中间点M与终点T之间路径的最少弯曲次数。

当中间点M与终点T都确定的情况下，其之间路径的最少弯曲次数CMT为常数。此时，整个路径的弯曲次数C的取值由CSM和CM这两个参数决定。因此，当CSM相同的情况下，整个路径的弯曲次数并不一定相同，这取决于CM的取值。

通过观察图1中的电缆敷设模型我们也很容易理解这个问题，在图1所示的模型中，在起点S与中间点c之间存在2条等长路径S-a-c与S-b-c，并且其弯曲次数都是1，在中间点c与终点T之间，路径的最少弯曲次数为1（路径c-d-T），但是当分别选取路径S-a-c与S-b-c作为最终结果时，其总的弯曲次数并不相同，原因就在于当选取路径S-a-c时，该路径在c点的弯曲次数为1，而选取路径S-b-c时，该路径在c点的弯曲次数为0。

通过上述分析我们知道，当在路径搜索过程中发现两条弯曲次数相同的等长路径时，我们并不能马上在两条路径之间做出取舍，而是应该将两条路径全部保留，在全部路径搜索完成后，对两条路径的总弯曲次数进行计算，选择弯曲次数较少的那一条路径作为最终结果。

下面给出整个改进A*算法的完整流程图，其中不同于常规A*算法的部分用虚线表示，如图3所示。

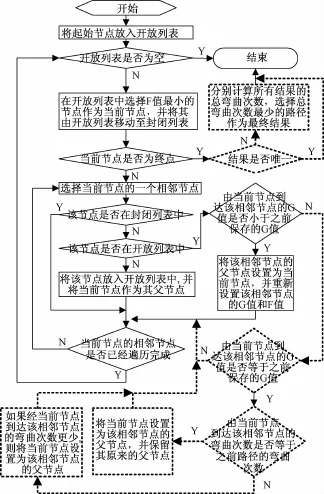
图3　改进A*算法的流程图

4　仿真结果

为了验证本文所给出的改进A*算法的实际效果，我们以酒钢集团铝电一期工程汽机房零米层中的部分电缆为例，在AutoCAD VBA开发环境下，对该算法进行了编程实现，并进行了仿真计算。酒钢集团铝电一期工程汽机房零米层的部分桥架模型如图4所示。

我们在该工程中随机选取了243根仪表控制电缆，分别利用常规A*算法和改进A*算法对这些电缆的敷设路径进行了仿真计算，通过观察仿真结果发现，对于某些电缆，在运用常规A*算法和改进A*算法进行路径搜索时，得到的敷设结果并不相同，结果如图5所示。

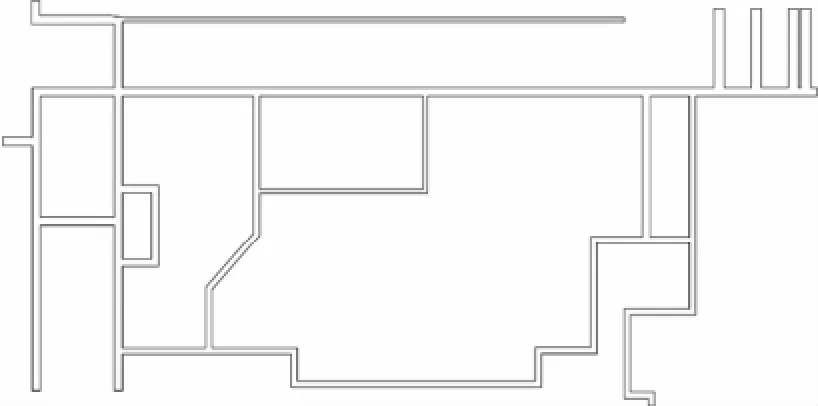
图4　酒钢铝电一期工程汽机房零米层部分桥架简化模型

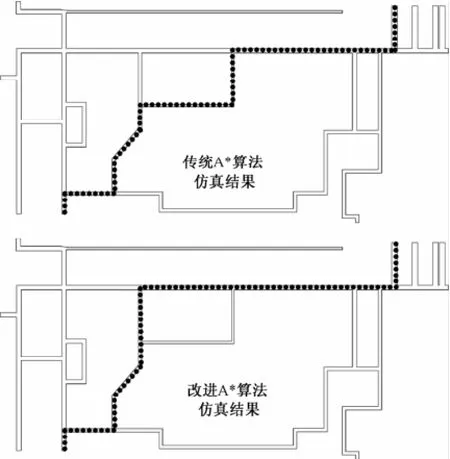
图5　传统A*算法与改进A*算法仿真结果对比

通过图5中两种算法仿真结果的对比可以发现，对于同一根电缆，在保证路径最优的前提下，改进A*算法所得结果与传统A*算法相比，电缆的弯曲次数减少了2次。对全部243根电缆的仿真结果进行统计汇总，其结果如表3所示。从表3可以看出，改进A*算法在保持电缆敷设总长度不变的前提下，其电缆的弯曲总次数相比于常规A*算法减少了约6%。

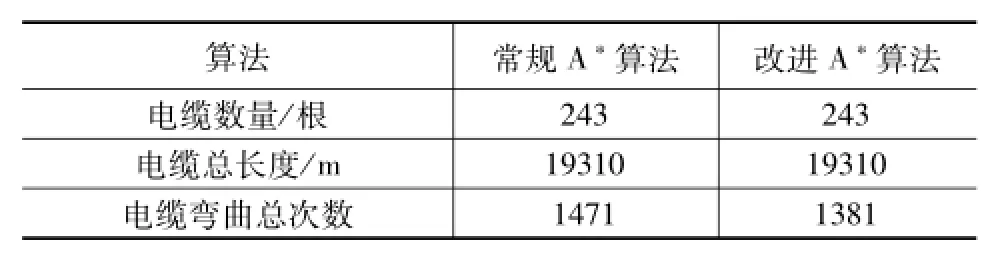
表3　仿真结果

5　实际应用过程中需要注意的问题

在实际应用本文所给出的考虑电缆弯曲次数的改进A*算法时，需要注意几个问题。

（1）路径长度的精度问题

在实际的电缆敷设设计时，电缆路径的长度往往都是由一定精度的小数来表示的。在实际操作过程中，由于电缆路径绘制不精确，或者开发环境中小数的精度过高等原因，往往会造成相同长度的两条电缆路径，其精确长度会有细微的差别。如果不进行额外的设置，算法会优先选择精确长度略短的那条路径，而这种路径长度上的细微差别在实际中是毫无意义的。因此，在进行电缆路径长度的比较时，不宜将精度设置得过高。

（2）缆流限制问题

利用改进A*算法进行电缆敷设的设计时，在某些情况下可能会造成部分电缆过分集中于某一条路径的情况，使得电缆路径的利用率不均衡。在这种情况下，可以通过对上述路径设置一个合理的缆流量限制值，来避免这种情况的发生。

6　结束语

本文所给的考虑电缆弯曲次数的改进A*算法，能够在保证路径最短的前提下，得到一条弯曲次数最少的电缆敷设路径。仿真结果显示，该算法能有效降低实际工程中电缆的总弯曲次数，这对降低电缆敷设施工的工作量和工作难度、提高电缆的可靠性都有着十分重要的意义。

［1］ 薛福连.35 kV及以下电力电缆故障的原因及对策［J］.电线电缆，2003（6）：38-40.

［2］ 吴明祥，毛琳明.一起220 kV电缆终端击穿故障原因分析［J］.浙江电力，2012（9）：10-20.

［3］ 刘永兴.一起所用变低压电缆起火燃烧事故原因分析及预防措施［J］.电气应用，2009，28（13）：44-46.

［4］ 安庆敏，徐爱东，陈志强，等.火力发电厂热控电缆敷设软件的开发与应用［J］.工业仪表与自动化装置，2011（6）：64-66.

［5］ 王永庆.人工智能原理与方法［M］.西安：西安交通大学出版社，2003.

［6］ Ni1sson N J.PrinciP1es of artificia1 inte11igence［M］.Pa1o A1to：Tioga Pub1ishing ComPany，1980：72-88.

APPlication of an Im Proved A*Algorithm in Cab le Laing Design

YANG Ya-wei1，WANG Lu2，WANG Fei1
（1.Shandong E1ectric Power Engineering Consu1ting Institute Co.，1td.，Jinan 250013，China；2.Shandong Education Training Center of Qua1ity and Technica1SuPervision，Jinan 250013，China）

In order to avoid the Prob1em that the resu1t of conventiona1 A*a1gorithm is on1y oPtim ization in Path 1ength and the Path curve quantity is not considered，an imProved A*a1gorithm is ProPosed in this PaPer，the resu1t of this a1gorithm is oPtimization in Path curve quantity on the Premise that the Path 1ength is shortest.The exPerimenta1data indicate that the curve quantity of cab1es is reduced after this a1gorithm is used in the cab1e 1aying design，which can reduce the difficu1t of cab1e 1aying construction and imProve the re1iabi1ity of the cab1es.

A*a1gorithm；cab1e 1aying；cab1e curve

TM202

A

1672-6901（2016）03-0032-04

2015-07-09

杨亚伟（1985-），男，硕士，工程师.

作者地址：山东济南市华龙路1665号电力咨询大厦1010室［250100］.