曲柄滑块机构系统动力学模型的建立

谭伟超

（江门职业技术学院，江门 529000）

曲柄滑块机构系统动力学模型的建立

谭伟超

（江门职业技术学院，江门 529000）

对于电动机驱动的机械系统，由于在运动过程中出现速度波动会导致运动中产生附加的动力，从而降低机械的寿命和工作可靠性。所以，需要研究机械运动速度的波动、调节方法以及驱动电机和机构。

曲柄滑块机构 动力学 FORTRAN 仿真

过去的三十年里，国内外学者对电动机与传统的机构系统开展了动力学分析。例如，张策[1-3]等人都对电动机-机构系统开展了一系列工作，并取得了不错的成果。

1　曲柄滑块机构的动力学模型

图1为曲柄滑块机构示意图，各连杆的尺寸代表符号已经标在图上。已知连杆质量m2，滑块质量m3，曲柄对其转动中心A的转动惯量为JA，其角速度为w1，连杆对其质心S2的转动惯量为JS2，其角速度为w2，两个极限位置角1ϕ、2ϕ，质心S2在x、y方向的速度分别为vS2x和vS2y，偏心距为e。

图1　曲柄滑块机构

根据动能定理，曲柄滑块系统在一段时间的动能增量应该等于作用于该系统所有外力所做的功。因此，曲柄滑块系统动能增量为：

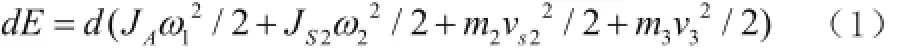
系统外力所做的功：

用等效转动惯量和等效力矩替代：

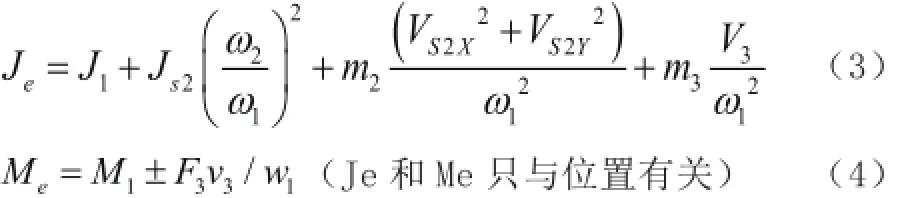
分别求解滑块在两处极点角度，滑块运动最右端时：

滑块运动到最左端时：

当加载在滑块上的负载为F3时，设lT为弹簧的自然状态长度,则可得如下两种情况：

（1）当ϕ2＞ϕ＞ϕ1，F3方向为正，则：

（2）当ϕ2＜ϕ＜ϕ1，F3方向为负，则：

2　稳定运动状态的动力学分析

机械的运转一般分为三个阶段：启动阶段、稳定阶段和制动阶段。在工程应用上，一般都想知道稳定运转状态下所发生的速度波动情况。在进行动力学分析时，多采用数值方法求解微分方程。为了求解曲柄滑块机构在稳定运转状态下的速度波动情况，可使用预估初值法，即任意给定一个初始角速度，然后求解运动方程。经过n个周期就可以满足周期性条件：

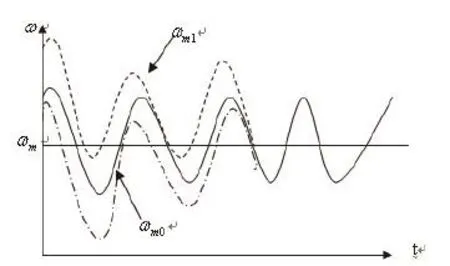
图2　预估初值法求解过程

如图2所示，实线是稳定运转时的实际运动规律。当取任意不同的初值时，求解运动方程的解以虚线表示。可以看出，虚线是逐步接近于稳定运转的实际运动规律。理论上，需要无限长的时间才能到达稳定下状态，实际上只要满足一定的控制精度（见式（10））就可以。

3　快速算法求解曲柄动力学微分方程

若等效力矩可以表达为两个函数之和，分别是角速度w的函数和转角ϕ的函数。那么，可以采用能量形式，建立其运动方程进行求解。

当采用电动机为原动机时，等效驱动力矩为：

等效阻力矩为：

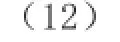
在1ϕ到2ϕ两个区间运用动能定理，得：

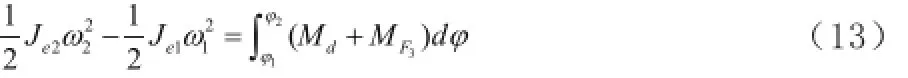
用梯形公式求积分，式子（13）可写成：

如图3所示，将等效构件的运动周期分为n等分，与机构等效构件的位置角ϕ1,ϕ2,⋅⋅⋅,ϕn+1相对应的等效阻力矩与转角有关的部分是已知量。

图3　快速算法

联立（11）、（12）和（13），可写为：

该方程是以w2为未知数的一元二次方程。假如w1已知，则可以求出w2的大小。

同理，对第i个区间，即iϕ和1iϕ+之间的区间，可以有如下递推公式：

式子：

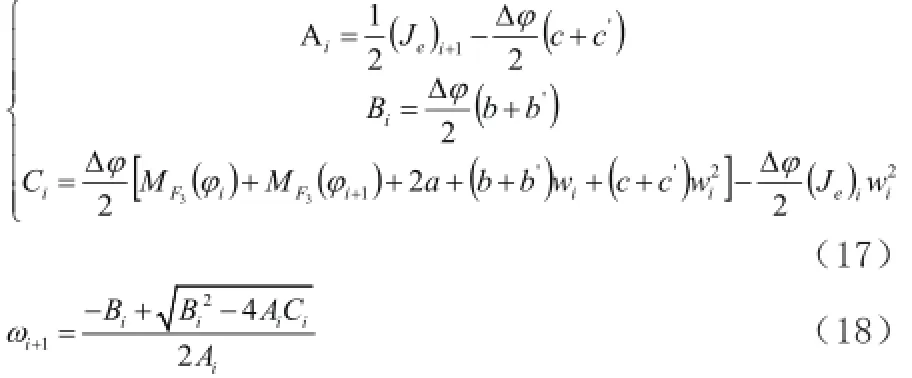
运用递推公式，当初始条件分别为ϕ=ϕ1, ω=ω0时，便可以求出每一个位置的角速度。

下面求解等效驱动力矩方程，图4为电机的机械特性。其中，AC运转时最稳定；当负载最大时，机械减速，输出力矩将会增大，并与外载荷达到新的平衡，AD段运转时不稳定；当外载荷增加导致转速下降时，输出力矩也下降，无法与外载荷平衡，造成转速进一步下降。因此，电机机械特性曲线主要在AC段，这是动力学分析中最常用到的。

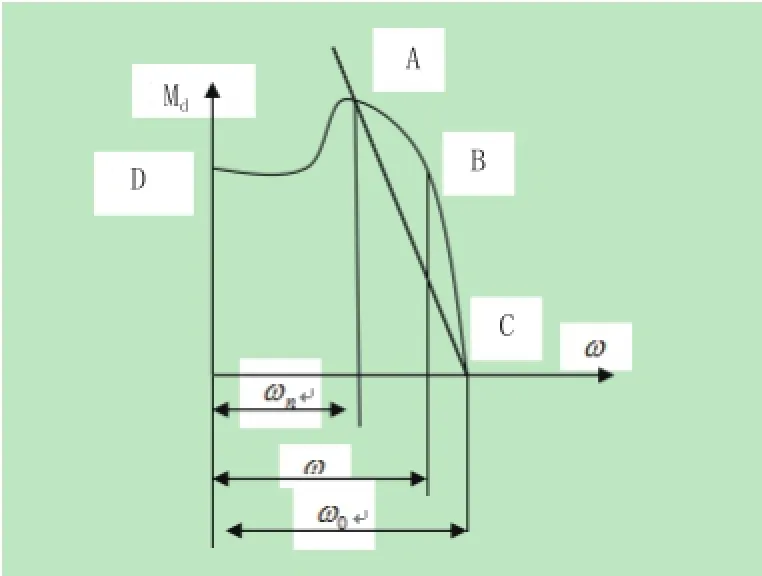
图4　电机机械特性曲线

ABC段可以通过A、B、C三点的二次抛物线表示。确定机械特性曲线上三个特征点的坐标分别为：A(Mn,ωn)，B(M,ω)，C(MO,ωO)，将A、B、C三点的坐标代入式（11），则可以得出一个线性方程组：

求解式（19），则可以得到系数a、b、c，从而求出等效驱动力矩方程。

4　本文小结

本文综合运用了机构的运动与动力学和数值分析方法，建立曲柄滑块机构的动力学模型，运用FORTRAN语言编程，求解出曲柄角速度的变化规律和理论曲线，以及不同转动惯量下曲柄角速度的运动规律。

[1]岳士岗，白师贤．输入转速波动对柔性连杆机构振动平衡特性的影响[J].机械科学与技术，1994，（1）：59-64.

[2]高广娣，秦伟.机械系统方案设计及性能测试综合试验台的设计[J].石河子大学学报，2007，（5）：630-632.

[3]刘建琴，张策.电机-弹性连杆机构系统的动力学分析[J].天津大学学报，1999，32（3）：265-269.

Slider-crank Mechanism Established System Dynamics Model

TAN Weichao
(Jiangmen Polytechnic, Jiangmen 529000)

In t he anal ysis of inst itutions, are generally assumed to be the movement of the movable member of the original determination, but the act ual movement of the movable member is a primary mechanism by the mass of each member institution, moment of inertia and the forces a cting on the machine, etc. different factors. For motor driven mechanical s ystems, due to the speed of the proces s in motion fluctuations resulted in additional power deputy campaign, which will reduce the mechanical reliability of life and wor k. So it needs to fluctuations in the mechanical movem ent speed and the method of their adjustment to study, it is necessary to drive the motor and mechanism studies.

sl ider-crank mechanism, kinetics, FORTRAN, simulation