一类双时滞食饵-捕食者模型的Hopf分支
2016-09-05高杏杏胡志兴廖福成
高杏杏,胡志兴,廖福成
(北京科技大学 数理学院,北京 100083)
一类双时滞食饵-捕食者模型的Hopf分支
高杏杏,胡志兴,廖福成
(北京科技大学 数理学院,北京 100083)
研究了一类具有双时滞及比率依赖功能性反应函数的食饵-捕食者模型。运用稳定性理论,分析了唯一的正平衡点在不同时滞状况下的稳定性,探讨了Hopf 分支的存在性,最后通过数值模拟验证了结论。
双时滞;食饵-捕食者模型;比率依赖;Hopf分支
食饵-捕食者模型是种群动力学中的重要分支,对其进行研究具有很大的实际意义。由于在自然界中,捕食关系受时滞的影响很大,因此,我们在相应的模型中也应充分考虑时滞的作用,如文献[1]~[2]。此外,近年来,越来越多的生物学研究表明,具有比率依赖的功能性反应函数往往更符合自然界中的实际情况。所谓比率依赖,即反应函数不仅与食饵的数量有关,还与捕食者的数量有关。在大多数情况下,尤其是捕食者必须寻找共享或竞争的食物时,更为合适的捕食率应是食饵与捕食者种群密度比值的函数,即依赖于比率的功能反应函数[3],如文献[3]~[5]均采用了具有比率依赖的功能反应函数,关于比率依赖的进一步阐述可参见文献[6]。另外,文献[7]~[8]均在基本的Leslie-Gower模型基础上进行研究,认为捕食者的种群密度采取logistic形式增长,而最大环境容纳量与食饵的种群密度成比例。此外,本文也参考了文献[9]关于周期解的描述。
在文献[1]中,研究了一类无量纲化后的Leslie-Gower模型:

(1)
式中,N(t)、P(t)分别表示t时刻食饵与捕食者的种群密度,α、β、δ均为正常数,τ为食饵与捕食者的时滞。
一方面,我们将功能反应函数变为具有Holling-III型比率依赖的反应函数;另一方面,考虑到τ的含义不同,即建立双时滞更为合理,因此,可建立如下模型:
(2)
式中,u(t)、v(t)分别表示t时刻的食饵与捕食者的种群密度;r1、r2分别为食饵与捕食者的内禀增长率;K为食饵生长的环境最大容纳量;c为捕食者的环境最大容纳量与食饵种群密度的比例系数;a、b均为功能性反应函数中的系数;τ1、τ2分别表示食饵自身增长的负反馈时滞和捕食者的成熟时滞;r1、r2、a、b、c均为正常数。
做以下变换,对式(2)进行无量纲化:

(3)
式中,m、h、r、q均为正常数。
1 正平衡点的稳定性及Hopf分支的存在性
考虑到模型的生态学意义,我们主要研究正平衡点E*的稳定性状况。
容易计算,若满足式(4):
mq<1+hq2
(4)

进一步计算,得到式(3)在E*(u*,v*)处的线性近似方程:
(5)
其中:
A3=rq2,A4=-rq
则式(5)的特征方程为:
λ2-(A1e-λτ1+A4e-λτ2)λ+A1A4e-λ(τ1+τ2)-
A2A3e-λτ2=0
(6)
其中λ为特征值。
情形1当τ1=τ2=0时,特征方程式(6)可化为:
λ2-(A1+A4)λ+A1A4-A2A3=0
其中
因此,若满足式(4)及
(7)
1+2hq2+h2q4-mq-mhq3>0
(8)
则A1+A4<0且A1A4-A2A3>0,即特征方程的两根均具有负实部,故模型在E*渐近稳定。
情形2当τ1>0,τ2=0时,特征方程式(6)可化为:
λ2-A1e-λτ1λ+A1A4e-λτ1=0
(9)
令λ=iω1(ω1>0)是该方程的根,分离实部与虚部可得:
(10)
两边分别平方后相加可得:
显然,该式有唯一正根ω10,并满足:
化简式(10)可得:
取τ1k=τ10,验证横截条件。令式(9)对τ1求导,则:
定理1当τ1>0,τ2=0并满足式(4)、式(7)、式(8)时,若τ1∈[0,τ10),则模型在E*处局部渐近稳定;若τ1>τ10,则模型在E*处不稳定。模型在τ1=τ10处出现Hopf分支。
情形3当τ2>0,τ1=0时,特征方程式(6)可化为:
λ2-A1λ+e-λτ2(A1A4-A2A3-A4λ)=0
(11)
令λ=iω2(ω2>0)是该方程的根,分离实部与虚部可得:
(12)
两边分别平方后相加可得:
显然,该式有唯一正根ω20,并满足:
化简式(12)可得:
k=0,1,2,…
取τ2k=τ20。验证横截条件。令式(11)对τ2求导,则:
定理2当τ2>0,τ1=0并满足式(4)、式(7)、式(8)时,若τ2∈[0,τ20),则模型在E*处局部渐近稳定;若τ2>τ20,则模型在E*处不稳定。模型在τ2=τ20处出现Hopf分支。
情形4当τ1=τ2=τ>0时,特征方程式(6)可化为:
两边同时乘以eλτ,即:
λ2eλτ-(A1+A4)λ-A2A3+A1A4e-λτ=0
(13)
令λ=iω(ω>0)是该方程的根,分离实部与虚部可得:
(14)
两边分别平方后相加可得:
ω8+a′ω6+b′ω4+c′ω2+d′=0
(15)
其中:
a′=-(A1+A4)2,b′=2(A1+A4)2A1A4-

为方便计算,令u=ω2,则式(15)可进一步化简为:
u4+a′u3+b′u2+c′u+d′=0
(16)
若满足:
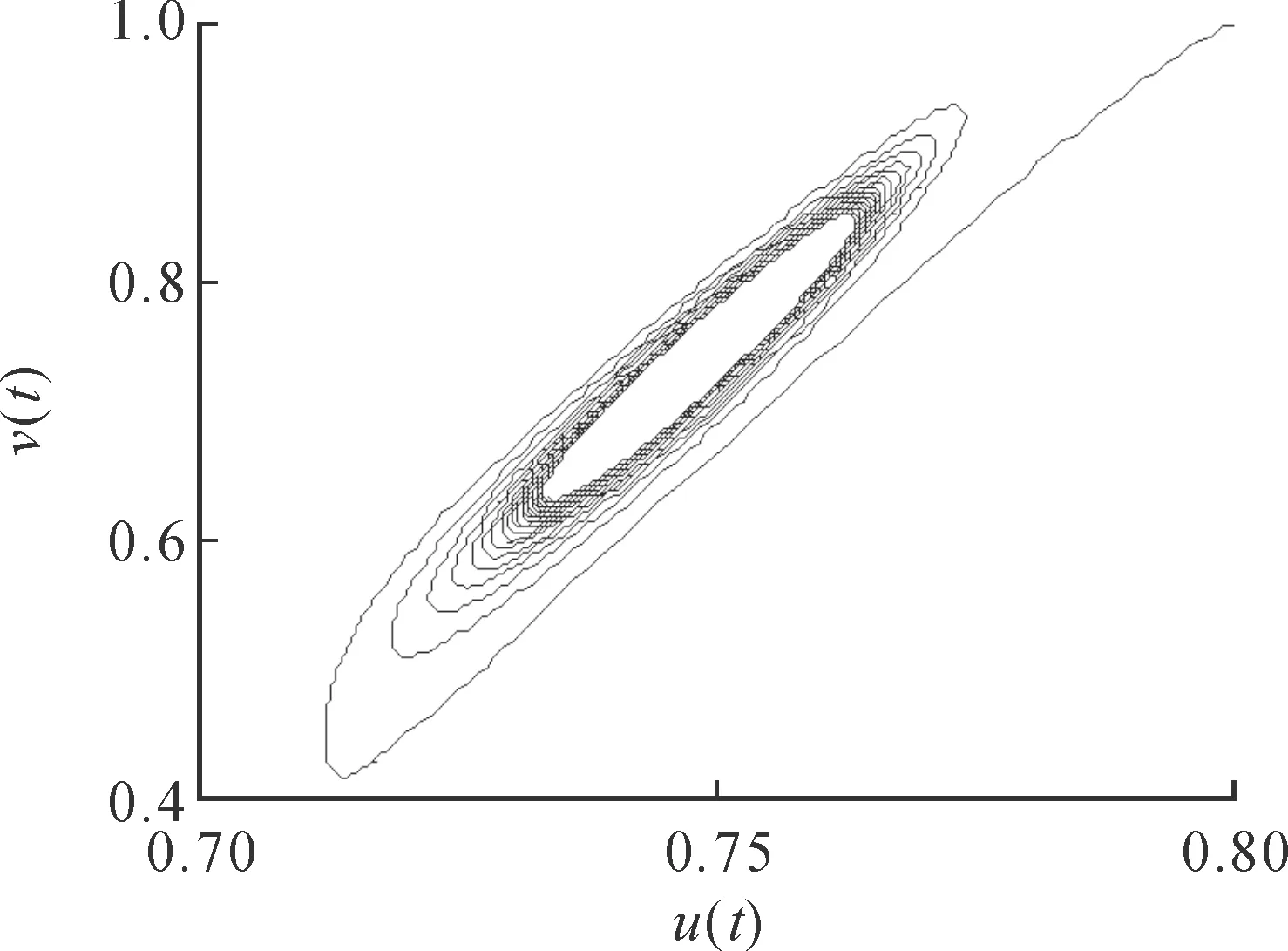
mq(1+hq2)<1+2hq2+h2q4 (17) 下面来验证横截条件。对式(13)两边关于τ求导,得: 其中: n=A1+A4-2ω0sinω0τ0 因此,若满足式(18): -wn+2fω0cosω0τ0≠0 (18) 定理3当τ1=τ2=τ≠0并满足式(4)、式(7)、式(8)、式(17)、式(18)时,若τ∈[0,τ0),则模型在E*处局部渐近稳定;若τ>τ0,则模型在E*处不稳定。模型在τ=τ0处出现Hopf分支。 情形5当τ1>0,τ2>0,τ1≠τ2时,考虑τ1在稳定的区间,τ2为参数。为不失一般性,在情形2中考虑式(3)。特征方程式(6)可化为: λ2-A1λe-λτ1-e-λτ2(A4λ+A2A3)+ A1A4e-λ(τ1+τ2)=0 (19) 令λ=iω2(ω2>0)是该方程的根,分离实部与虚部可得: (20) 其中: g=A4ω2+A1A4sinω2τ1,H=A2A3-A1A4cosω2τ1 两边分别平方后相加可得: f1(ω2)+2f2(ω2)sinω2τ1+ 2A1A2A3A4cosω2τ1=0 (21) 其中: 令: G(ω2)=f1(ω2)+2f2(ω2)sinω2τ1+ 2A1A2A3A4cosω2τ1 显然,若满足式(22): (22) 验证横截条件。令式(19)对τ2求导,可得式(24)。 (23) (24) (25) (26) 其中: x=A1A4sinω*(τ1+τ*)+A4ω*cosω*τ*-A2A3sinω*τ* y=A1A4cosω*(τ1+τ*)-A2A3cosω*τ*-A4ω*sinω*τ* A1cosω*τ1-A4cosω*τ* 2ω*+A1sinω*τ1+A4sinω*τ* 因此,若满足式(27): Px+Qy≠0 (27) 则 定理4当τ1>0,τ2>0,τ1≠τ2并满足条件式(4)、式(7)、式(8)、式(22)、式(27)时,固定τ1∈[0,τ10),若τ2∈[0,τ*),则模型在E*处局部渐近稳定;若τ2>τ*,则模型在E*处不稳定。模型在τ2=τ*处出现Hopf分支。 在本节,利用MATLAB对以上各种不同的时滞情况进行了数值模拟,并验证了相应定理。 情形2τ1>0,τ2=0。取m=1,q=1,h=3,r=0.3。满足定理1的条件,计算可得临界值τ10=1.3644。图1和图2分别为τ1<τ10和τ1>τ10时,解的相图。 图1 τ1=1.3<τ10时模型在E*处稳定Fig.1 E*is stable when τ1=1.3<τ10 图2 τ1=1.9>τ10时模型在E*处经历Hopf分支Fig.2 E*undergoes Hopf bifurcation when τ1=1.9>τ10 情形3τ2>0,τ1=0。取m=1,q=1,h=3,r=0.3。满足定理2的条件,计算可得临界值τ20=6.1930。图3和图4分别为τ2<τ20和τ2>τ20时解的相图。 图3 τ2=6.0<τ20时模型在E*处稳定Fig.3 E*is stable when τ2=6.0<τ20 图4 τ1=6.3>τ20时模型在E*处经历Hopf分支Fig.4 E*undergoes Hopf bifurcation when τ1=6.3>τ20 情形4τ1=τ2=τ>0。取m=0.5,q=1,h=0.05,r=0.1。满足定理3的条件,计算可得临界值τ0=2.7801。图5和图6分别为τ<τ0和τ>τ0时解的相图。 图5 τ=2.7<τ0时模型在E*处稳定Fig.5 E*is stable when τ=2.7<τ0, 图6 τ=2.9>τ0时模型在E*处经历Hopf分支Fig.6 E*undergoes Hopf bifurcation when τ=2.9>τ0 情形5当τ1>0,τ2>0,τ1≠τ2。取m=1,q=1,h=3,r=0.3,τ1=0.5∈[0,τ10)。满足定理4的条件,计算可得临界值τ*=5.9811。图7和图8分别为τ<τ*和τ>τ*时解的相图。 图7 τ=5.9<τ*时模型在E*处稳定Fig.7 E*is stable when τ=5.9<τ* 图8 τ=6.3>τ*时模型在E*处经历Hopf分支Fig.8 E*undergoes Hopf bifurcation when τ=6.3>τ* 本文研究了一类具有双时滞的食饵-捕食者模型。与原有的单时滞模型相比,它区分食饵与捕食者的成熟时滞,即建立双时滞,这显然更合理;此外,本文采用了比率依赖型功能反应函数,即反应函数不仅与食饵的数量有关,也与捕食者的数量有关,这更符合自然界的实际情况。通过以上分析,首先得到了模型存在的唯一正平衡点;其次讨论了它在不同时滞情况下的稳定性状况,得到了其产生Hopf分支的条件;最后进行了数值模拟,验证了文中的各个定理。研究表明:时滞的变化对于种群的生长具有很大影响,一旦超越临界时滞,模型就会经历Hopf分支,产生周期解。文章最终将有助于我们更好地理解自然界中的捕食关系,研究种群的实际生长情况。 [1]CANAN Ç.Stability and Hopf bifurcation in a delayed ratio dependent Holling-Tanner type model[J].Applied Mathematics and Computation,2015,255:228-237. [2]ZHANG Zizhen,YANG Huizhong,FU Ming.Hopf bifurcation in a predator-prey system with Holling type III functional response and time delays[J].Journal of Computational and Applied Mathematics,2014,44(1):337-356. [3]唐秋林,吴美云.基于比率依赖的Leslie捕食扩散模型的Turing不稳定性[J].安徽大学学报(自然科学版),2010,34(5):5-10. TANG Qiulin,WU Meiyun.Turing instability in a ratio-dependent Leslie predator-prey model with diffusion[J].Journal of Anhui University (Natural Sciences),2010,34(5):5-10. [4]PALLAV J P,PRASHANTA K M,KAUSHIK K L.A delayed ratio-dependent predator-prey model of interacting populations with Holling type III functional response[J].Nonlinear Dynamics,2014,76(1):201-220. [5]郑宗剑.双时滞比率依赖Holling-Ⅳ和Leslie型捕食-食饵系统的Hopf分支[J].北华大学学报,2015,16(1):9-16. ZHENG Zongjian.Hopf bifurcation of ratio-dependent Holling IV and Leslie type predator-prey system with two delays[J].Journal of Beihua University,2015,16(1):9-16. [6]ABRAMS P A,GINZBURG L R.The nature of predation:prey dependent,ratio dependent or neither[J].Trends in Ecology & Evolution,2000,15(8):337-341. [7]YANG Wensheng.Global asymptotical stability and persistent property for a diffusive predator-prey system with modified Leslie-Gower functional response[J].Nonlinear Analysis,2013,14(3):1323-1330. [8]SHARMA S,SAMANTA G P.A Leslie-Gower predator-prey model with disease in prey incorporating a prey refuge[J].Chaos,Solitons & Fractals,2015,70:69-84. [9]刘凯丽,窦家维.一类脉冲L-V系统的周期解和全局渐近性质[J].西安理工大学学报,2012,28(2):235-239. LIU Kaili,DOU Jiawei.The periodic solutions and globally asymptotic properties of L-V system with impulsive effects[J].Journal of Xi’an University of Technology,2012,28(2):235-239. (责任编辑周蓓) Hopf bifurcation in a predator-prey model with double time delays GAO Xingxing,HU Zhixing,LIAO Fucheng (School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China) This study focuses on a predator-prey model with double time delays and ratio-dependent functional response.The stability theory is used to analyze the stability in the unique equilibrium in different time-delay conditions and explore the existence of the Hopf bifurcation.And the numerical simulation is conducted to justify the conclusions in the end. double time delays; predator-prey model; ratio-dependent; Hopf bifurcation 10.19322/j.cnki.issn.1006-4710.2016.01.18 2015-06-15 国家自然科学基金资助项目(11471034,61174209);北京科技大学冶金工程研究院基础研究基金资助项目(YJ2012-001) 高杏杏,女,硕士生,研究方向为生物数学。E-mail:gxx1021@126.com 胡志兴,男,教授,博士,研究方向为生物数学。E-mail:huzhixing@ustb.edu.cn O175 A 1006-4710(2016)01-0100-06



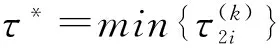

2 数值模拟







3 结 论
