单位方体上沿曲面的振荡积分的Sobolev有界性*1

赵俊燕， 朱相荣

（浙江师范大学数理与信息工程学院，浙江金华　321004）

参考文献：

单位方体上沿曲面的振荡积分的Sobolev有界性*1

赵俊燕， 朱相荣

（浙江师范大学数理与信息工程学院，浙江金华321004）

研究了欧氏空间R2中单位方体Q2=［0，1］2上沿曲面（t，s，tksj）的振荡奇异积分算子

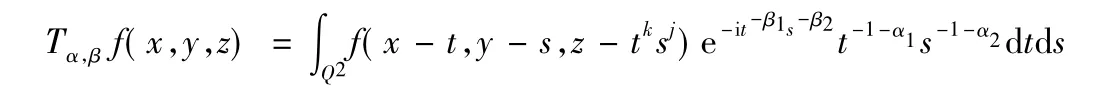
超奇异振荡积分算子；Sobolev空间；有界性；多参数

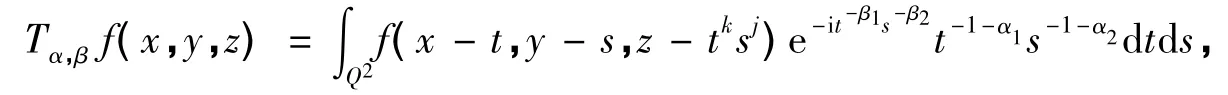
where（t，s，tksj）is a surface on R3，β1＞α1≥0，β2＞α2≥0 and（k，j）∈R2.As applications，some Sobolev boundedness results of rough singular integral operators on the product spaceswere obtained.

0　引言

在单参数的情形，设b＞a≥0，（x，y）∈R2，定义沿曲线（t，tk）的振荡奇异积分算子

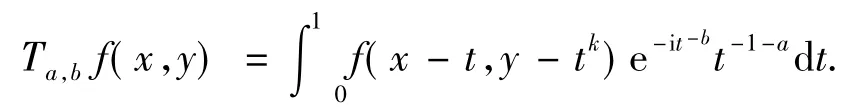
算子Ta，b在调和分析及其相关主题的研究中有着深刻的背景，它与Hilbert变换、沿曲线的Hilbert变换及强奇异积分算子密切相关［1-2］.历史上，Zielinski［3］首先研究了这类沿曲线的带振荡因子的超Hilbert变换，并证明了：若k=2，则Ta，b在L2上有界当且仅当b≥3a.这一结果随后被Chandarana［4］改进为：若k≥2，则Ta，b在L2上有界当且仅当b≥3a.同时，文献［4］还证明了：若b＞3a且1+则Ta，b是Lp（R2）上的有界算子.文献［5］改进了参数p的范围，并且给出了新的证明.进一步的研究可参见文献［6-7］等.另一方面，受单参数情形的启发，叶晓峰［8］研究了单位正方形上的算子

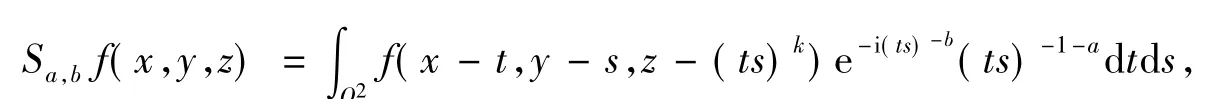
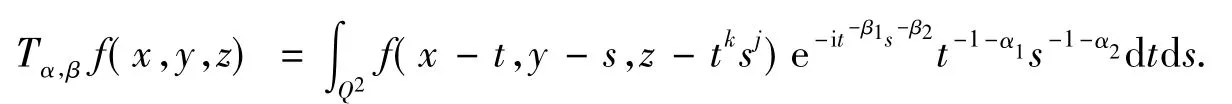
其中：β1＞α1≥0；β2＞α2≥0.进一步的研究可参见文献［10］等.文献［9］的结论可概括为以下定理：

定理1［9］假定β1＞3α1≥0，β2＞3α2≥0且对任意的α=（α1，α2），β=（β1，β2），

1）若（k，j）≠（-β1，-β2）且

＜γ，则‖Tα，βf‖Lp（R3）≤C‖f‖Lp（R3）；

2）若（k，j）=（-β1，-β2），则Tα，β不是L2（R3）到L2（R3）有界的.

定理2［9］假定β1＞2α1≥0，β2＞2α2≥0或者j=1，k∈R.则

设

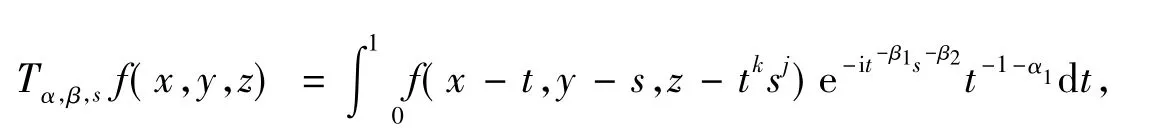
则

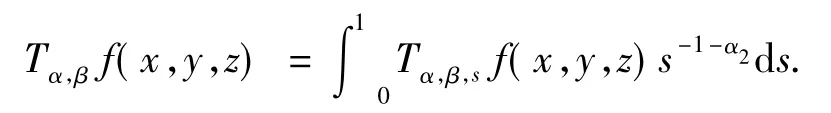
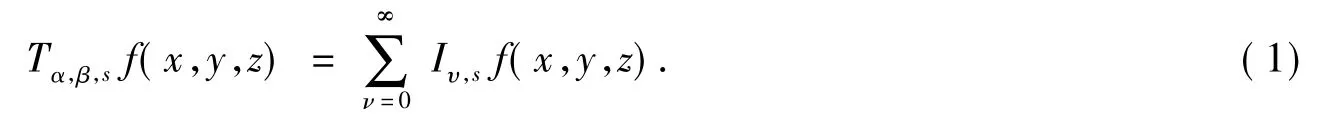
式（1）中，

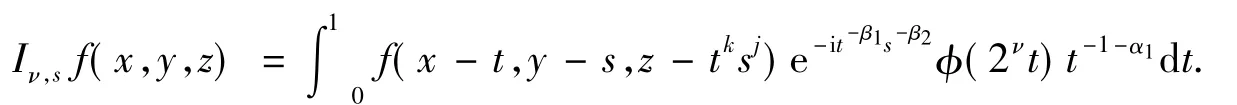
当α1，α2，β1，β2＞0时，定义新的算子

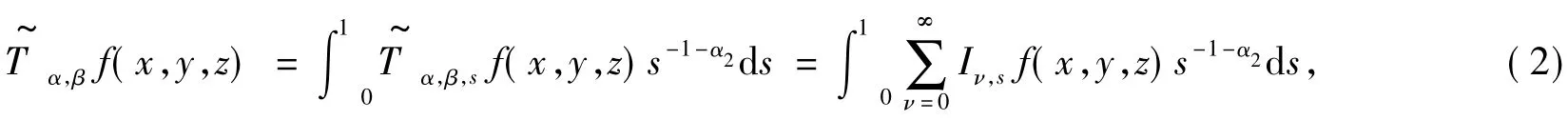
且当β1＞α1＞0，β2＞α2＞0时满足

本文研究了算子Tα，β在非齐次Sobolev空间上的有界性.首先回顾非齐次Sobolev空间的相关概念.

设s∈R，f∈S'（Rn），Bessel位势Bs是作用在f上的卷积算子，其定义可由如下Fourier变换的形式给出：

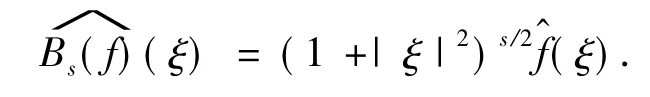
类似地，Riesz位势Rs是作用在f上的卷积算子，其定义也可由Fourier变换的形式给出：

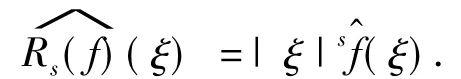
定义1［11］设s为实数，1＜p＜∞.非齐次Sobolev空间（Rn）是由所有满足Bs（u）∈Lp（Rn）的广义函数u∈S'（Rn）组成的空间，其范数定义为‖u‖Lps （Rn）=‖Bs（u）‖Lp（Rn）.齐次Sobolev空间是由所有满足下列性质的缓增分布u∈S'（Rn）所组成的空间：

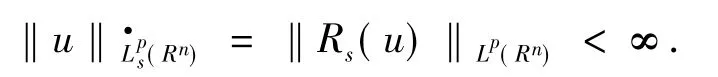
当s＞0时，

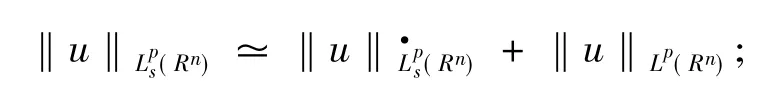
当k为非负整数时，

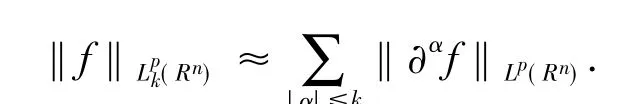
下面给出本文的主要结果：

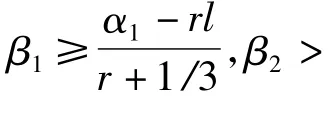
在此基础上，本文还建立了Tα，β从（R3）到Lp（R3）的有界性.

定理4设α1，α2，β1，β2均为正数，（k，j）≠（-β1，-β2），

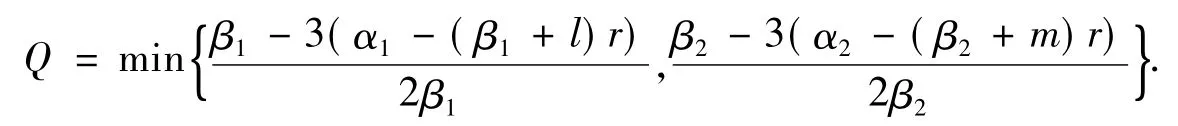
其中：l=min｛1，k｝；m=min｛0，j｝.对任意的r≥0，若则存在不依赖于f∈S（R3）的常数C，使得

注2当r=0时，定理4的结果覆盖了定理1的1）.

由定理3和定理4不难得到以下推论：

推论1设β1＞3α1≥0，β2＞3α2≥0，（k，j）≠（-β1，-β2），并令

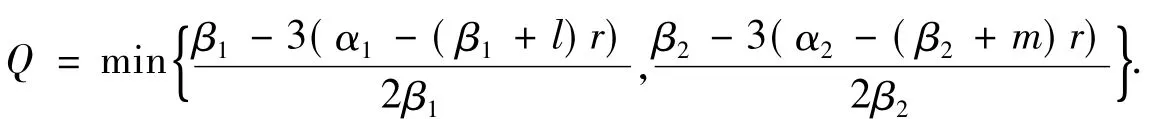
相应于定理2，可得到如下结果：

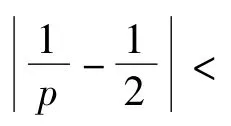
为了叙述方便，本文仅给出定理3和定理4的证明，定理5的证明类似可得，限于篇幅，不再赘述.同时将推论1应用于乘积空间上的某类粗糙核奇异积分算子的Sobolev有界性问题.此外，表示指标p的对偶指标.为方便起见，本文用字母C，C0表示不依赖于所涉及空间的主要参数的正常数，且其值也未必处处相同.表达式A～B是指存在常数C，C0，使得表示存在常数C，使得f≤Cg.

1　引理

首先介绍一个简单的引理，它将在定理3的证明中起到很好的作用.

其中ψ（t，s）=tξ1+t-β1s-β2+ξ2s+ξ3tksj.关于Jν，s（ξ）有如下估计：

引理1［9］存在正常数C，使得

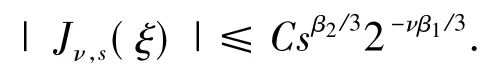
其中，C只依赖于指标β1，β2，k，j及函数Ω，与ν和ξ无关.

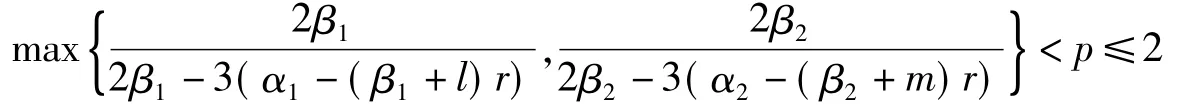
接下来介绍另一个引理，它对的情形下定理4的证明非常重要.

引理2对任意的1＜q＜2及一切正整数N，有

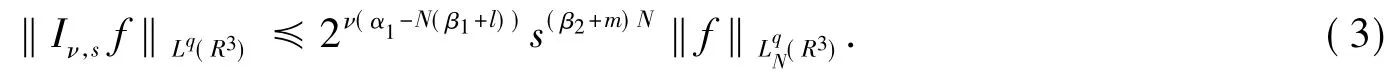
式（3）中，Iν，sf的定义如前所述.

证明先验证N=1时式（3）成立.由分部积分得

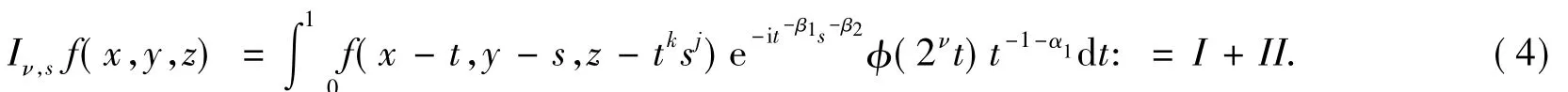
式（4）中：

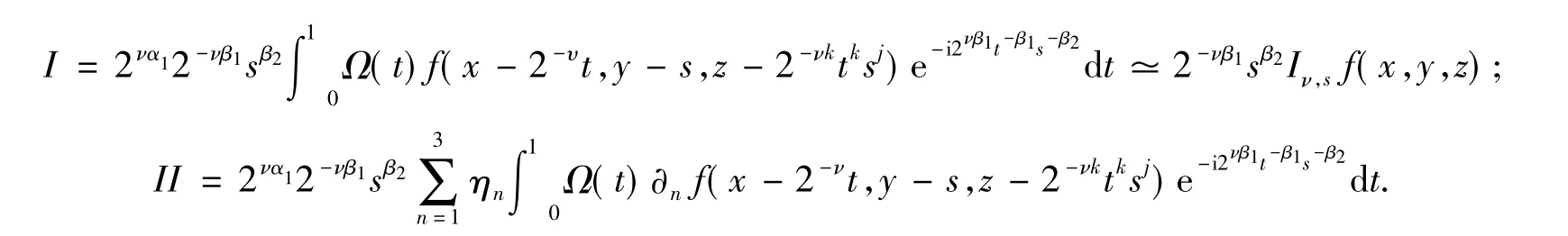
其中，η=（η1，η2，η3）=（2-ν，0，2-νksjktk-1）.现分别估计I和II.对II，由Minkowski不等式可知

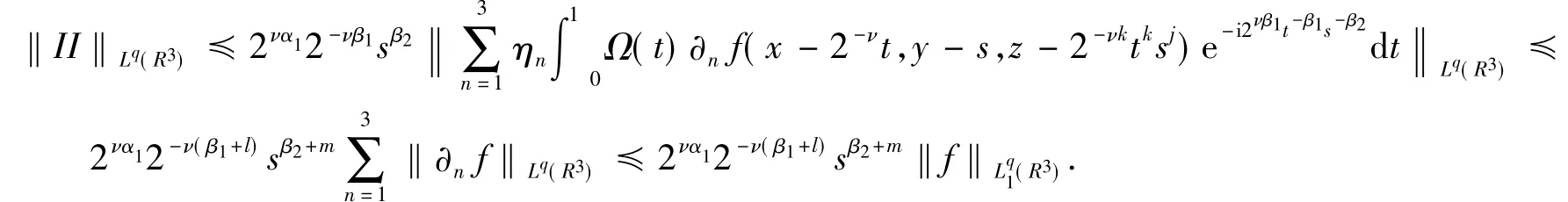
对I，由Minkowski不等式显然有

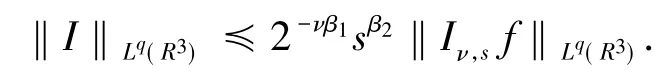
对I运用S-1次分部积分，重复以上步骤，再取充分大的S，使得

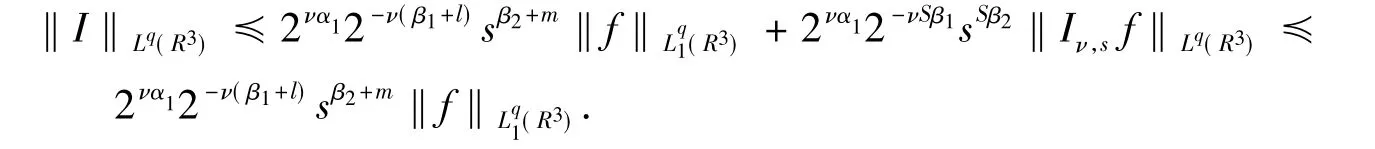
从而

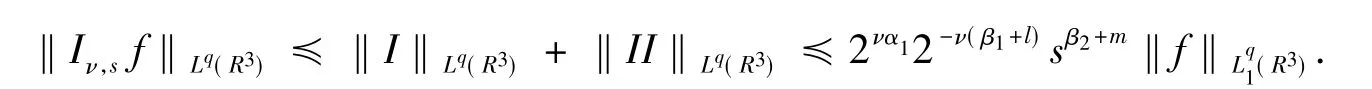
N=1的情形由此得证.

假设引理2中的估计对N-1成立，这意味着

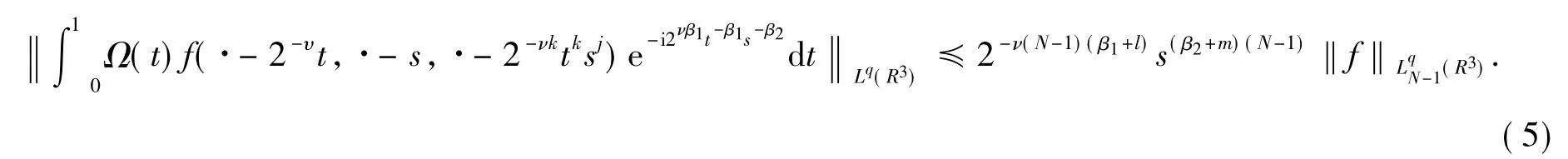
式（5）中，N为不小于2的正整数.根据归纳假设只需证明式（3）对N仍成立.类似于N=1的情形，运用分部积分得

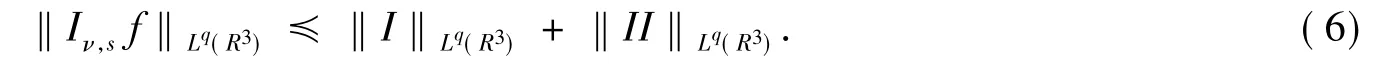
由归纳假设（5）知，对II有如下估计：

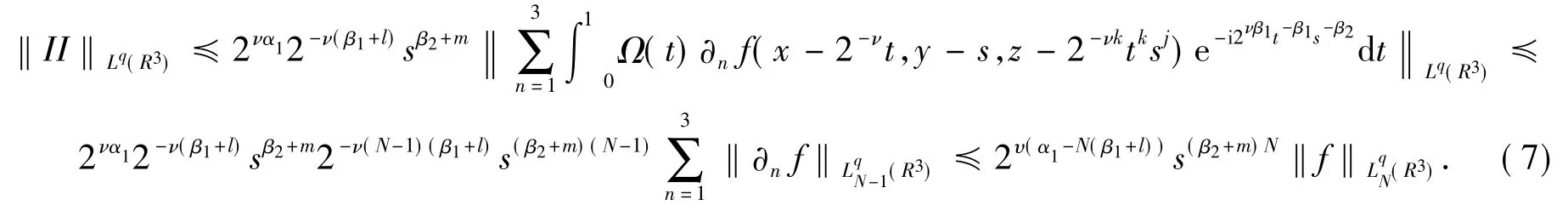
类似地，对I作S-1次分部积分，再取充分大的S，使得

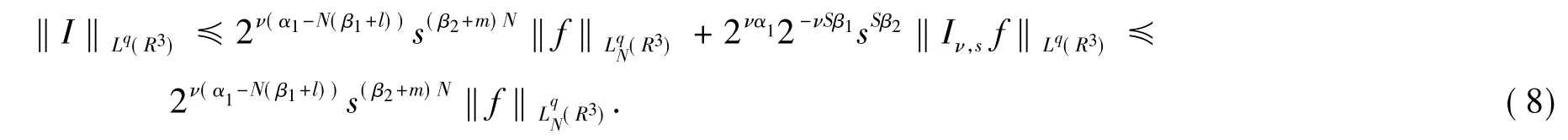
2　定理3　的证明

证明由式（2）应用Minkowski不等式得

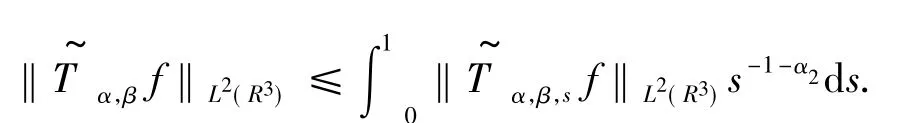
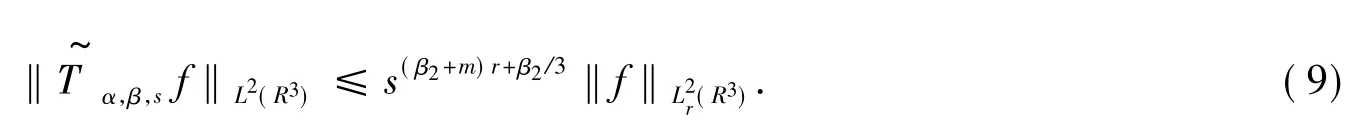
应用Plancherel定理得，

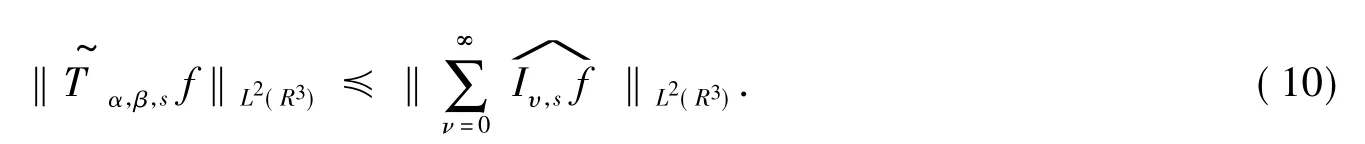
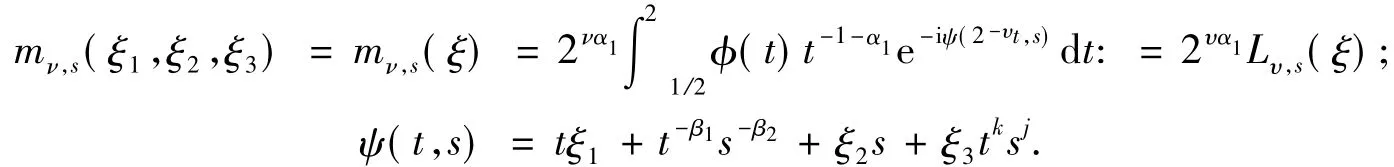
结合式（9）和式（10），要证明定理3，只需说明关于ξ∈R3一致成立即可.为此需要以下命题：

命题1对任意的r＞0，存在与ξ和ν无关的常数C＞0，使得

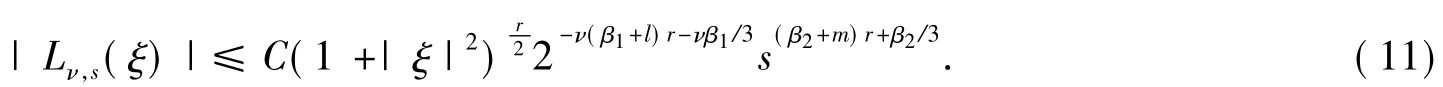
首先说明如何利用命题1证明定理3，命题1的证明将置于本节最后.

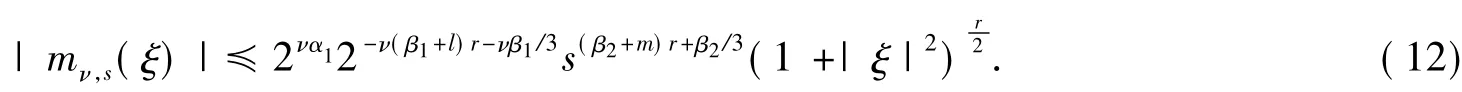
进而，由Plancherel定理有

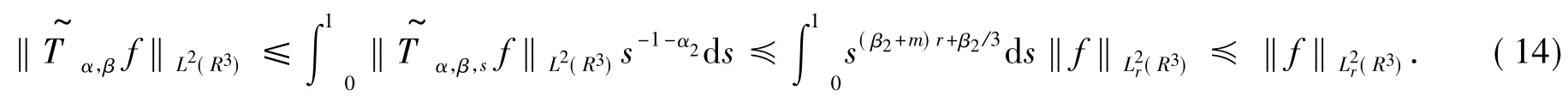
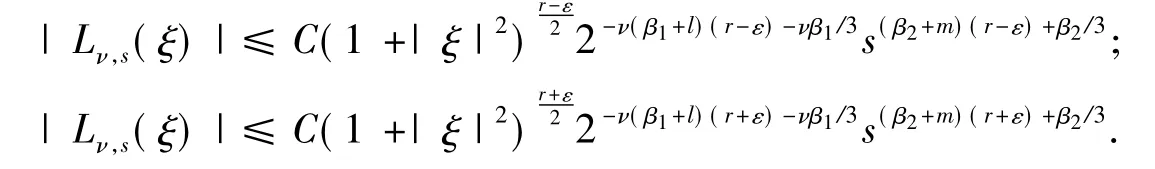
由此可得

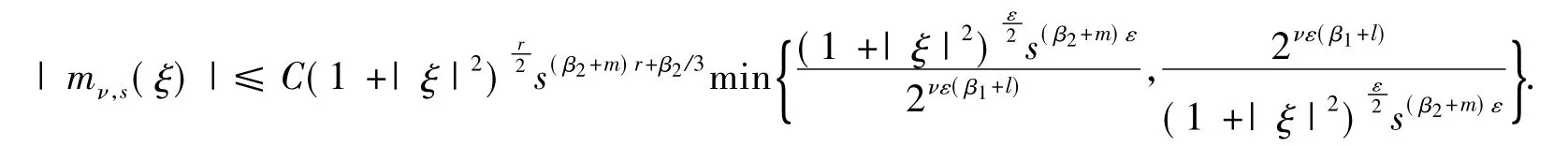
关于ξ∈R3一致成立.由此，当时α，β是从（R3）到L2（R3）的有界算子.定理3证毕.

最后给出命题1的证明.对任意的r＞0，存在自然数τ，满足τ-1＜r≤τ.下面对τ运用归纳法来证明.

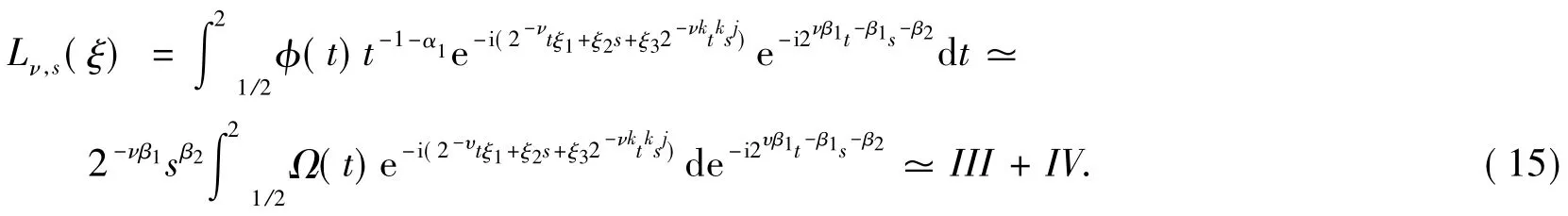
式（15）中：

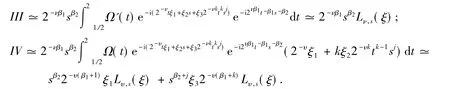
由引理1得

注意到l=min｛1，k｝，m=min｛0，j｝，|ξi|≤|ξ|，i=1，2，3.于是

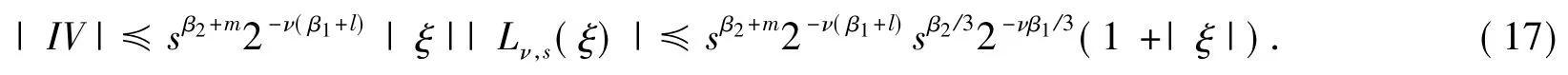
对III重复上述步骤，并继续分部积分N-1次得

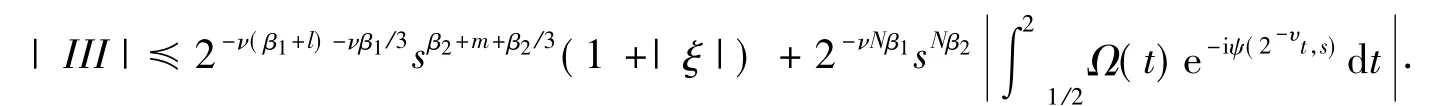
由引理1，可取充分大的整数N，使得

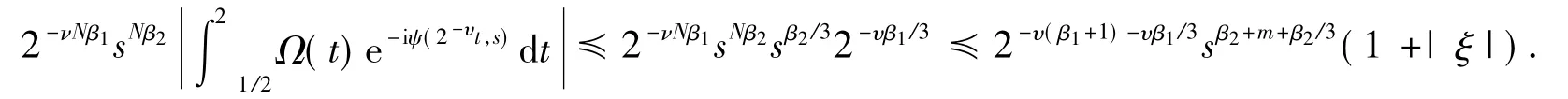
从而得到

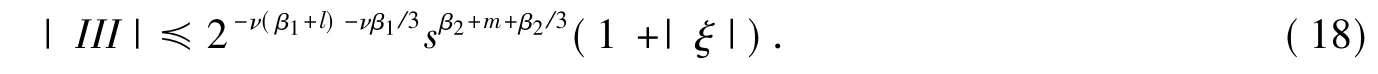
由式（15）、式（17）和式（18）可得

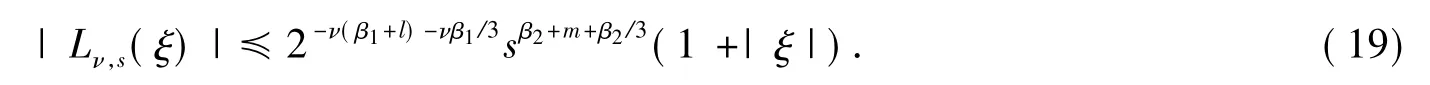
式（19）结合r=0时的估计（16）得，对一切0≤r≤1，有

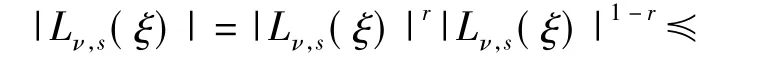
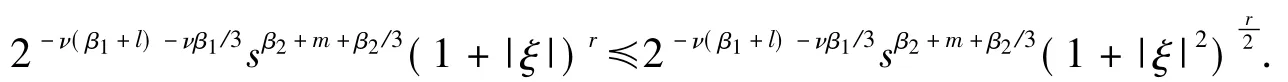
第2步，假设命题1对满足τ-1＜r≤τ的r均成立，其中τ为不小于2的正整数，那么只需再证明命题1对τ＜r≤τ+1也成立即可.对Lν，s（ξ）作分部积分可得形如式（15）的表达式：

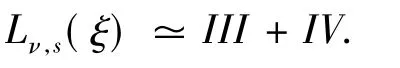
由归纳假设可得关于IV的下述估计：

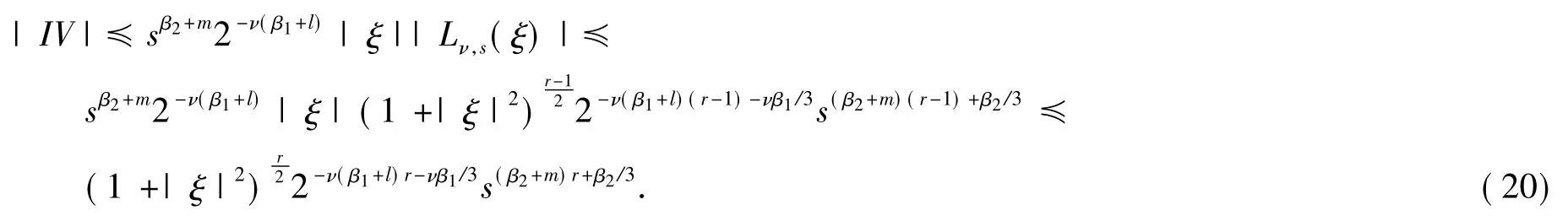
类似地，对III作N-1次分部积分，可得

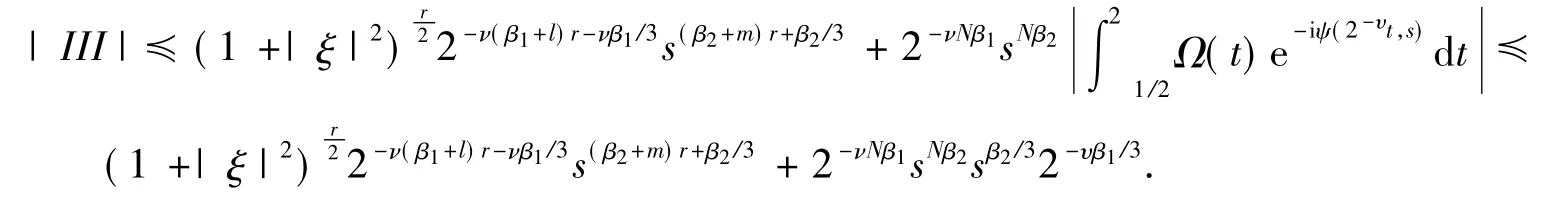
取充分大的整数N，使得

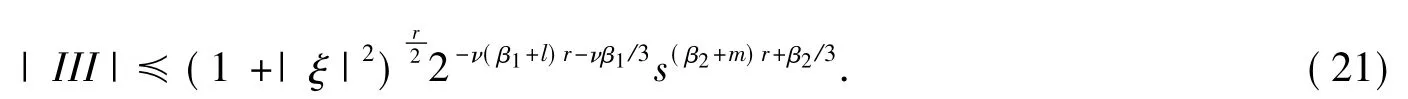
综合式（20）和式（21）的估计，命题1对满足τ＜r≤τ+1的r也成立.命题1证毕.

3　定理4　的证明

由Minkowski不等式易得Iν，s在Lq（R3）上的有界性：

对r∈（0，N），在式（3）和式（22）之间运用插值定理得

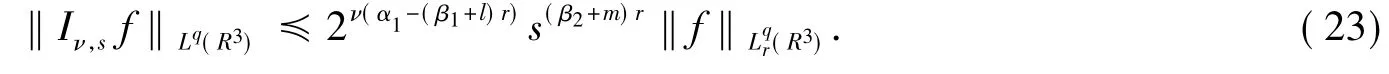
由N的任意性知，式（23）对一切r＞0都成立.由式（12）结合Plancherel定理易得

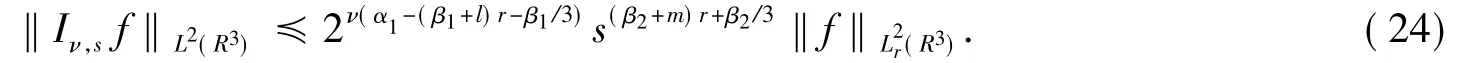
对p∈（q，2），在式（23）和式（24）之间再次运用插值定理得

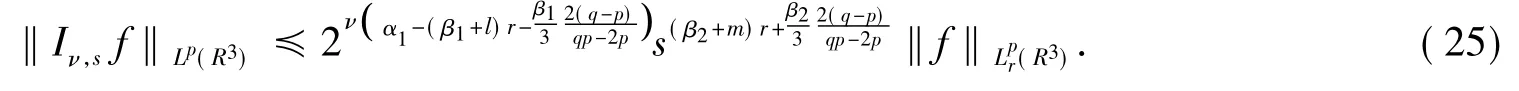
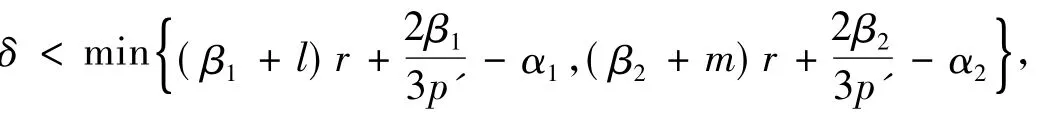
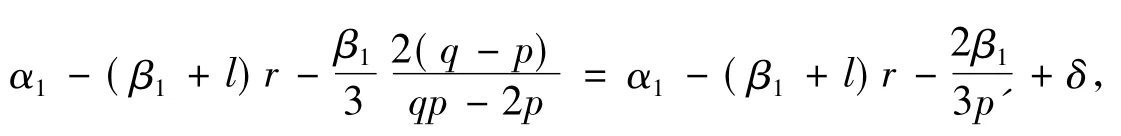
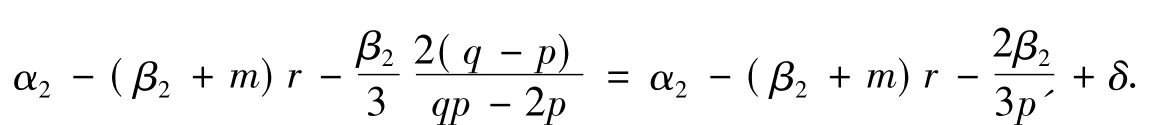
从而由式（25）及Minkowski不等式可得，对一切的正实数r，有

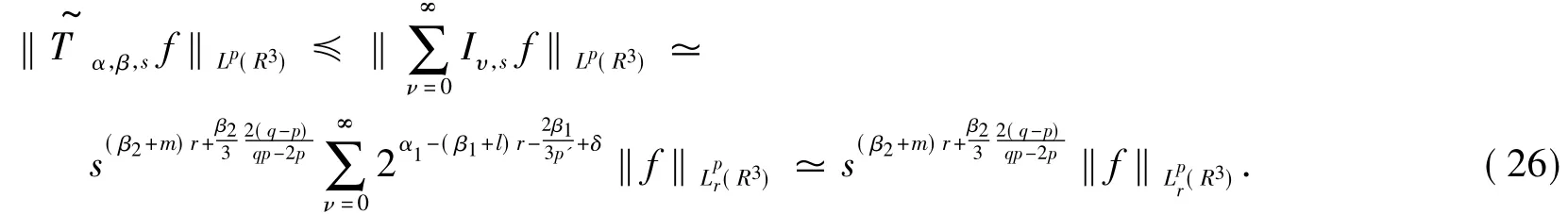
再由式（26）及Minkowski不等式可得，对一切的正实数r，有的情形由此获证.

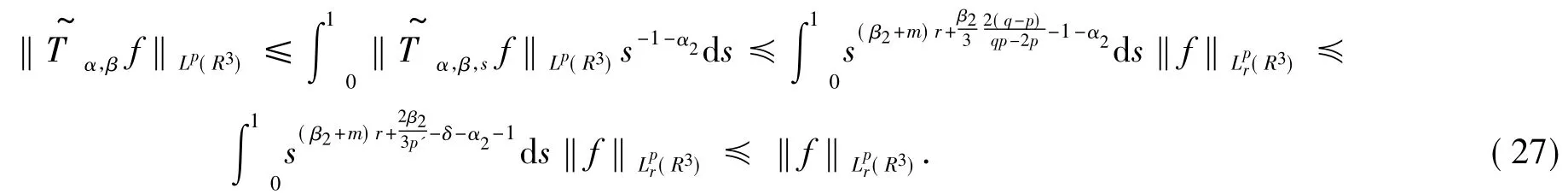
为完成定理4的证明，只需再讨论如下情形：

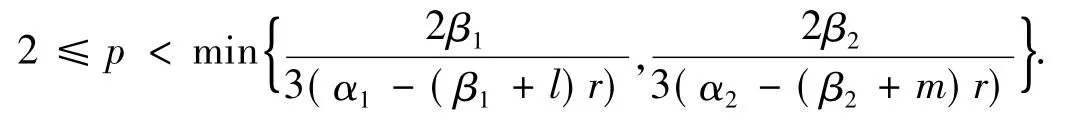
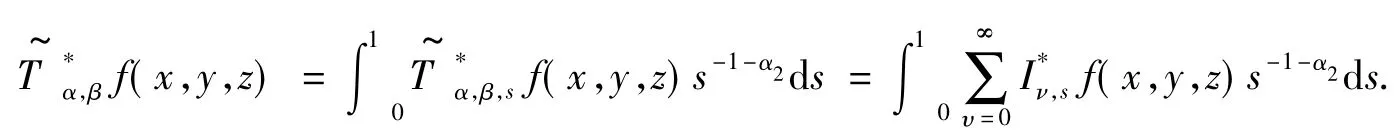
其中，

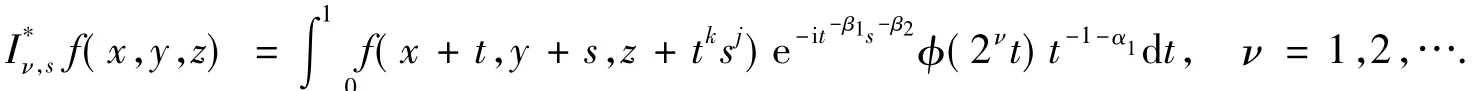
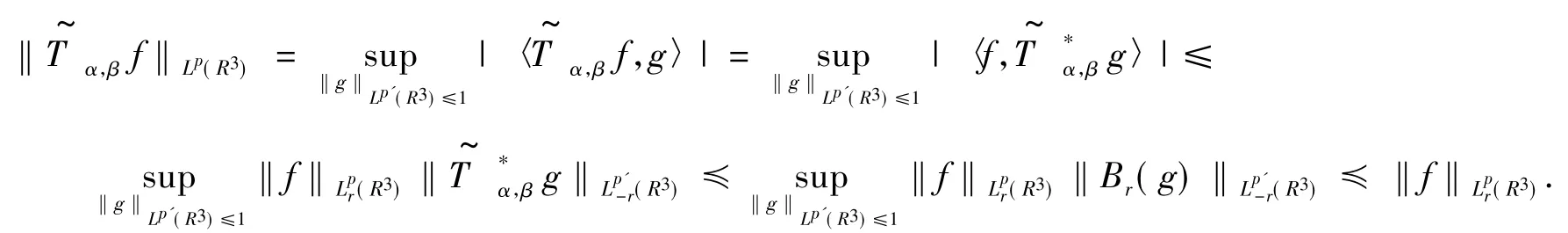
上述最后一个不等号可由Bessel位势的半群性质得到.定理4证毕.

4　乘积空间上的粗糙核奇异积分算子的So b o l e v有界性

设n≥2，m≥2，k≥1，Sd-1为Rd上的单位球面，Bd=Bd（0，1）为Rd上的单位球（d=n或m）.下面研究粗糙核奇异积分算子

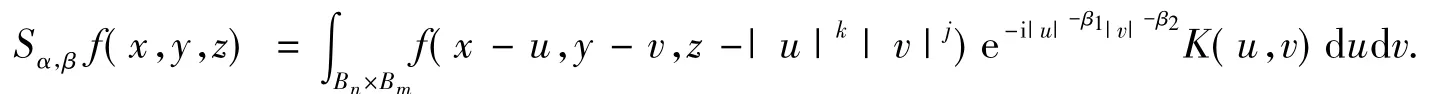
其中：（x，y，z）∈Rn×Rm×R；K（u，v）=|u|-n-α1|v|-m-α2Ω（u，v）且Ω（u，v）∈L1（Sn-1×Sm-1）关于变量u，v均为零阶齐次函数.得到如下结果：

定理6设β1＞3α1≥0，β2＞3α2≥0，（k，j）≠（-β1，-β2），并令

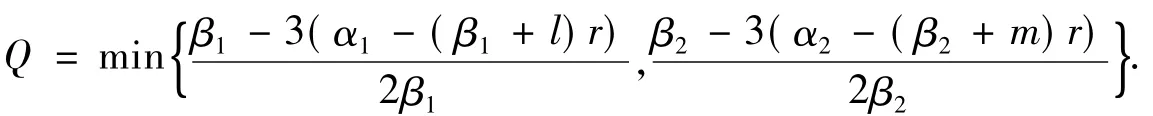
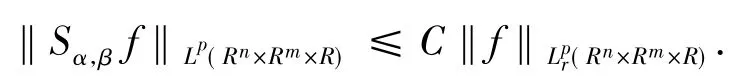
证明由极坐标变换得

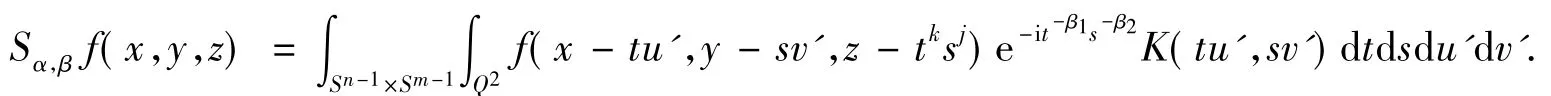
其中：K（tu'，sv'）=Ω（u'，v'）t-1-α1 s-1-α2；u'，v'分别为u，v方向的单位向量.由Minkowski不等式知，要证定理6，只需证

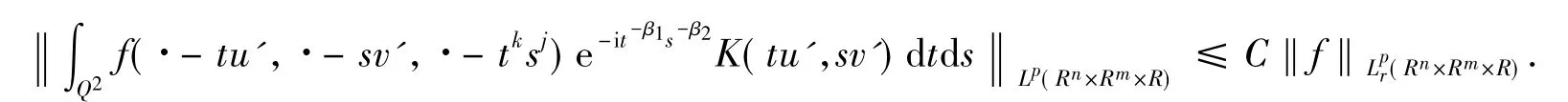
其中，C与（u，v）无关.

记SO（d）为Rd上的旋转群，对于固定的u'和v'，取A∈SO（n），B∈SO（m），使得Au'=1=（1，0，…，0）为Sn-1的北极，Bv'=e=（1，0，…，0）为Sm-1的北极.定义函数g满足g（Ax，By）=f（x，y），则‖g‖Lp（Rn×Rm×R）=‖f‖Lp（Rn×Rm×R），且f（x-tu'，y-sv'）=g（Ax-t1，By-se）.因此，由变量代换得

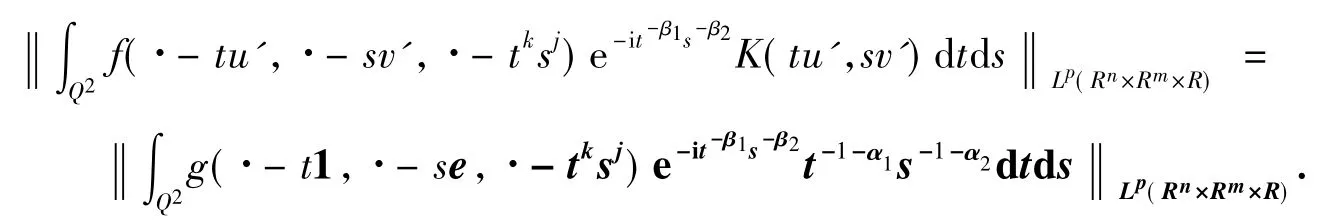
应用累次积分及推论1即可得定理6的结果.定理6证毕.

参考文献：

［1］Fefferman C.Inequalities for strongly singular convolution operators［J］.Acta Math，1970，124（1）：9-36.

［2］Sjölin P.An Hpinequality for strongly singular integrals［J］.Mat Z，1979，165（3）：231-238.

［3］ZielinskiM.Highly oscillatory singular Integrals along curves［D］.Madison：University ofWisconsin，1985.

［4］Chandarana S.Lp-bounds for hyper-singular integral operators along curves［J］.Pacific JMath，1996，175（2）：389-416.

［5］王梦，陈杰诚，范大山.某类沿曲线的振荡积分［J］.数学年刊：A辑中文版，2007，28（1）：49-56.

［6］Chen Jiecheng，Fan Dashan，Wang Meng，et al.Lpbounds for oscillatory hyper Hilbert transforms along curves［J］.Proc Amer Math Soc，2008，136（9）：3145-3153.

［7］Chen Jiecheng，Fan Dashan，Zhu Xiangrong.Sharp L2boundedness of the oscillatory hyper Hilbert transform along curves［J］.Acta Math Sin：Engl Ser，2010，26（4）：653-658.

［8］叶晓峰.函数空间及算子的有界性［D］.杭州：浙江大学，2006.

［9］Fan Dashan，Wu Huoxiong.Certain oscillatory integrals on unit square and their applications［J］.Sci in China Ser A，2008，51（10）：1895-1903.

［10］Chen Jiecheng，Fan Dashan，Wu Huoxiong，et al.Oscillatory integrals on unit square along surfaces［J］.Front Math China，2011，6（1）：49-59.

［11］Stein EM.Harmonic analysis：real-variablemethods，orthogonality and oscillatory Integrals［M］.Princeton：Princeton University Press，1993.

（责任编辑陶立方）

The boundedness of certain oscillatory integrals on unit square along surfaces on Sobolev spaces

ZHAO Junyan， ZHU Xiangrong
（College of Mathematics，Physics and Information Engineering，Zhejiang Normal University，Jinhua 321004，China）

Let Q2=［0，1］2be the unit square in two dimension Euclidean space R2.It was studied the boundedness properties from Sobolev spaces（R3）to Lp（R3）of the oscillatory integral operatorτα，βdefined on the set S（R3）of Schwartz test funtions f by

hyper singular oscillatory integral；Sobolev space；boundedness；multiparameter

O174.2

A

1001-5051（2016）02-0129-10

10.16218/j.issn.1001-5051.2016.02.002

*收文日期：2015-09-17；2015-11-27

国家自然科学基金资助项目（11271330；11471288）；浙江省自然科学基金资助项目（010015）

赵俊燕（1989-），女，河南南阳人，硕士研究生.研究方向：调和分析及其应用.

朱相荣.E-mail：zxr@zjnu.cn