面向可靠性和能耗优化的可压缩数据收集方案*
2016-09-02王建新中南大学信息科学与工程学院湖南长沙410083
李 鹏,王建新(中南大学信息科学与工程学院,湖南长沙410083)
面向可靠性和能耗优化的可压缩数据收集方案*
李鹏,王建新
(中南大学信息科学与工程学院,湖南长沙410083)
现有的无线传感器网络(WSNs)数据收集方法无法在耗费较低开销的同时保证数据收集的可靠性。基于压缩感知(CS)理论,设计了基于指数核函数的稀疏矩阵和基于准循环低密度奇偶校验(LDPC)码的测量矩阵来用于节点的数据采集,以最大化网络生命周期为目标,将测量值传输问题建模为汉密尔顿回路问题,并提出了一种基于树分解的数据收集路径优化算法。仿真实验结果表明:所提方案在数据重构误差和能耗方面的性能要优于目前典型的数据收集方法。
无线传感器网络;数据收集;压缩感知;稀疏矩阵;测量矩阵;树分解
0 引言
在无线传感器网络(wireless sensor networks,WSNs)[1]的诸多应用中,均要求传感器节点以无差错形式将监测数据传输至Sink。但由于无线通信链路的高失效率、节点资源受限以及环境恶劣等原因,使得节点间通信受到干扰,产生丢包问题,导致可靠的数据传输难以得到保障。文献[2]设计了一种基于压缩感知和纠删码(compressive sensing erasure encoding,CSEC)的数据收集方案。然而,该方案在一定程度上是以牺牲节点的能耗为代价来提高数据收集可靠性,在真实传感器网络中的实际应用价值不大。文献[3]针对可压缩数据收集(compressive data gathering,CDG)方案[4]在有损信道中进行数据收集的不足,提出了最大稀疏随机调度(sparsest random scheduling,SRS)的数据收集方案。然而,该方案仅根据感知数据间的空间相关性来提高数据收集可靠性,因此,它容易受到网络节点初始分布的影响,鲁棒性较差。
针对上述方法的不足,本文以压缩感知理论为基础,提出一种面向可靠性和能耗优化的可压缩数据收集方案,并通过仿真实验也表明了该方案的有效性。
1 问题建模
设N个传感器节点和1个Sink节点被随机地分布在一个面积为N×N平方米的正方形区域A内。整个WSNs构成一个连通的无向图。WSNs具有如下性质:1)所有节点在部署后保持静止,节点的传输半径相同。2)网络中任意节点之间的链路可能存在丢包现象,且发生丢包的位置无法预测。3)采用能量均衡的非均匀分簇路由协议(distributed energy-balanced unequal clustering routing protocol,DEBUC)[5]对网络进行分簇。节点的初始能量不统一,节点在其自身能量耗光后,不能进行补充。
现有的基于压缩感知的数据收集方法[6]只适用于理想条件,当网络中部分链路中断而导致丢包现象发生后,会导致部分节点的测量值无法有效地被收集,此时,如果处于中断链路端点的节点重要程度较高,则会严重影响到数据收集的质量,导致网络应用可靠性较低。为此,本文研究的问题是:如何设计稀疏矩阵和测量矩阵来应对数据丢失,以及如何对数据收集路径进行优化,最终实现数据收集的高精确度与网络生命周期的最大化。
2 节点上的数据处理
2.1稀疏矩阵设计
在密集部署的大规模WSNs中,不同节点的感知数据之间通常具有时空相关性。本文采用如下的指数核函数κ(xi,xj)对感知数据间的相关性进行衡量

式中dij为第i个传感器和第j个传感器之间的距离。σ为函数的宽度参数,可以通过最大似然估计或贝叶斯学习机制得到。根据式(1)可知,对于拥有N个节点的WSNs而言,其所有感知数据的相关性可以表示为

根据式(2)可知,R属于托普利兹(Toeplitz)矩阵,它可以对角化为。其中,ΨR为由R的正交特征向量组成的基函数,Γ为一个对角矩阵,它的非零元素由R的特征值组成。依据上述分析,本文采用ΨR作为感知数据的稀疏矩阵,即有x=ΨRs。
2.2测量矩阵设计
已有的测量矩阵[7]大多将焦点集中在如何提高数据收集精度和降低数据收集能耗,但很少考虑到如何应对数据收集过程中的传输丢包问题,可靠性不高。为此,本文提出采用分块矩阵的思路来设计测量矩阵,具体设计过程分为两个部分:1)对于叶子节点而言,采用单位矩阵I来收集它们的数据,即对叶子节点的数据不经压缩采样就直接收集。2)对于非叶子节点而言,则利用其数据传输的信道编码校验矩阵来设计测量矩阵。一般而言,信道编码校验矩阵的列向量很容易被稀疏化,且任意的两个列向量之间具有线性无关的特性,容易满足RIP性质。为此,提出一种基于准循环低密度奇偶校验(low density parity check,LDPC)码[8]的方法来构造测量矩阵'。综上所述,本文要设计的测量矩阵为:=[I/']。
理论分析[8]表明:如果一个给定的二进制奇偶校验矩阵在信道编码/解码中具有良好性能,则该矩阵作为测量矩阵同样能够精确地实现基于压缩感知的信号重构。而对于网络存在丢包情况下基于压缩感知的数据收集应用而言,除了保证数据收集质量以外,如何尽可能少地消耗节点能量也是必须考虑的问题。因此,本文从降低节点能耗的角度出发,结合准循环低密度奇偶检验(low density parity check,LDPC)码具有的稀疏性、高纠错性等性质,通过搜索适当的单位矩阵移位次数,提出了一种基于准循环LDPC码的测量矩阵构造方法。其主要步骤如算法1所示。
算法1:基于准循环LDPC码的测量矩阵构造算法
1)首先,构造一个由M×N个大小为S×S的零方阵组成矩阵CM'。
2)随机选择ai1和a1j来构造移位矩阵SMai1和SMa1j,0≤ai1,a1j<S,0<i≤M,1<j≤N,并用SMai1和SMa1j来替代CM'中对应位置的零方阵。
3)随机选择aij来构造移位矩阵SMaij,0≤aij<S,并用SMaij来替代CM'中对应位置的子矩阵。

5)对CM中的所有列向量做归一化处理,然后抽取M个线性无关向量来填充压缩感知测量矩阵'的前M个列向量,即:。
最后通过前M列的线性组合来表示测量矩阵中的剩余N-M个列向量,从而得到'。
2.3簇内数据收集
综上所述,各个传感器节点依据上述设计的稀疏矩阵ΨR和测量矩阵对各自的感知数据进行压缩采样后通过单跳或多跳的方式上传到各自所属的簇头节点,然后由Sink来找到一条最优的路径将各个簇头的测量值收集上来,并采用重构算法来还原各个节点的原始数据。
3 数据收集路径优化
一般而言,Sink可以采用多条路径来收集各个簇头上的测量值,因此,为了节省网络能量,本文的目标是要找到一条最优路径,使得每个簇头只需被访问一次就能将所有簇头的测量值收集上来,该问题可以看作一个起点和终点都是Sink的汉密尔顿回路问题,它属于NP难题。考虑到WSNs中节点的数目是有限的,本文提出一种基于树分解[9]的测量值传输路径优化算法来解决该问题。
算法2:基于树分解的测量值传输路径优化算法
输入:由簇头和Sink组成的无向连通图G'=(V',E')
输出:测量值的传输路径P
1)Sink发送一个查询包到各个簇头,各个簇头根据Sink的广播路径返回各自的测量值:
从图G'=(V',E')的Sink顶点出发进行广度优先搜索,记录得到的图G'的顶点访问序列集合为VaS,
If G'中任意两个顶点的度数之和<|V'|+1,Then
从VaS选取一条可以回到Sink的序列作为传输路径P,算法结束。
Else转步骤(2);
2)首先,从图 G'=(V',E')中任意删除一个节点v'(v'∈V')和与v'相关联的边,并在余下的图中补充边,将v'的邻居节点组织成团结构。然后,采用最大势搜索策略[10]来逐个消元图G'=(V',E')的所有节点,可获得具体的消元顺序,然后依据该消元顺序可构造得到图G'=(V',E')的一个非平凡树分解Γ=(T,),树宽为k。对于每一个i∈,Vi=∪j,j=i or j是i的孩子节点,则
Ei=E'∩(Vi×Vi);
3)对每个节点i∈,计算包含了节点i参与的所有回路集合的哈希表HTi(i,θ),θi,|HTi|≤2k+1;
4)对于θi,在HTi(i,θ)中找到一条最短的回路P,使得i∩P=θ,
If不存在回路Then设置HTi(i,θ)=-∞;
Else返回P;
∥HTi(i,θ)是图G'=(V',E')上的一个汉密尔顿回路P
5)对于所有的节点 i∈,以自底向上的方式计算HTi(i,θ),重复执行步骤(3)~(5)直到中所有的节点都处理完毕。
4 仿真实验
采用Matlab 2012作为仿真工具,利用CitySee系统[11]测得的温度数据作为测试数据来验证本文方案的性能。实验过程中用到的主要仿真参数设置:数据包长度为1000 b;发送1bit数据所需的能量为10nJ;接收1bit数据所需的能量为50 nJ;单个节点每次数据收集所需能量为1000 nJ;数据重构采用OMP算法。
主要考察了本文方案在与目前较为典型的SRS方案和CSEC方案在数据重构误差和能耗方面的性能对比情况。实验结果取50次仿真的平均值。其中,数据重构误差采用下式进行衡量

式中x为原始数据,^x为其重构值。
图1给出了丢包率变化情况下三种方案的重构误差实验结果。可以看到,随着丢包率的增加,三种方案的重构误差都在增加,但是本文方案的性能最优,CSEC次之。另外,SRS方案和CSEC方案的数据重构误差随着丢包率的增加趋向于线性增加,而本文方案的数据重构曲线更为平坦,这表明本文方法的鲁棒性更强,在应对网络丢包方面更为有效,当丢包率达到15%时,本文方案的重构误差相比于SRS方案和CSEC方案降低了约42.6%和31.2%。
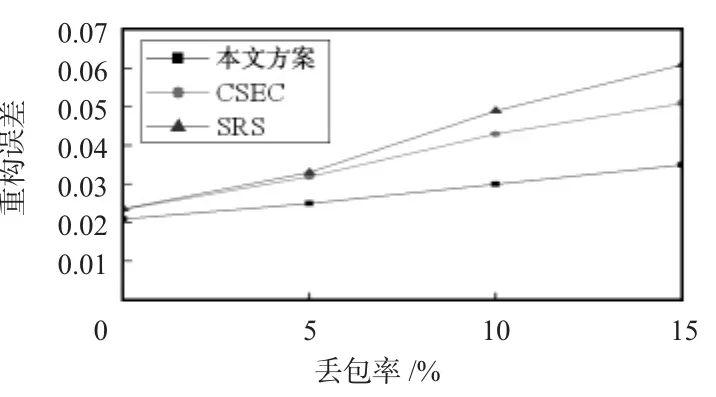
图1 不同方案的重构误差比较Fig 1 Reconstruction error comparison of different schemes
图2给出了本文方案与SRS方案和CSEC方案的能耗比较情况。可以看到:网络能耗与重构误差成反比关系,本文方案的能耗最低。随着数据收集应用对于重构误差的要求降低,本文方案的优势越发明显,当重构误差仅仅要求为0.1时,本文方案的能耗相比于CSEC方案和SRS方案分别节省了约56.1%和41.6%。
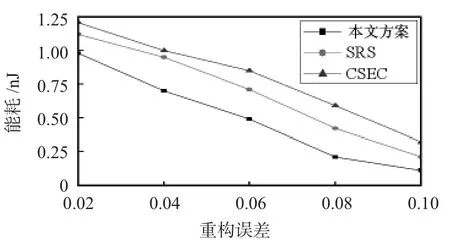
图2 不同方案的能耗比较Fig 2 Energy consumption comparison of different schemes
5 结束语
本文提出了一种面向可靠性和能耗优化的可压缩数据收集方案,首先设计了稀疏矩阵和测量矩阵用于节点上的数据收集,然后提出了一种基于树分解的数据收集路径优化算法。仿真实验结果表明:本文方案无论是数据重构精度还是能耗都要优于已有的方法。下一步工作的重点是:1)采用压缩感知理论,研究基于多个固定Sink的数据收集路径优化方案;2)采用压缩感知理论,研究基于单个移动Sink的数据收集可靠性方案。
[1]陈岩,谭婷,高峰,等.水质监测无线传感器网络节点双电源设计[J].传感器与微系统,2015,34(10):93-95.
[2]Charbiwala Z,Kim Y,He Ting,et al.Compressive oversampling for robust data transmission in sensor networks[C]∥The 29th IEEE Conference on Computer Communications,Joint Conference of the IEEE Computer and Communications Societies(INFOCOM),San Diego,CA,USA:IEEE,2010:1-9.
[3]Wu Xuanguo,Yang Panlong,Jung Taeho,et al.Compressive sensing meets unreliable link:Sparsest random scheduling for compressive data gathering in lossy WSNs[C]∥The 20th Annual International Conference on Mobile Computing and Networking (MOBICOM),Maui,HI,USA:ACM,2014:13-22.
[4]Luo Chong,Wu Feng,Sun Jun,et al.Efficient measurement generation and pervasive sparsity for compressive data gathering[J].IEEE Transactions on Wireless Communications,2010,9(12):3728-3738.
[5]蒋畅江,石为人,唐贤伦,等.能量均衡的无线传感器网络非均匀分簇路由协议[J].软件学报,2012,23(5):1222-1232.
[6]Zheng Haifeng,Yang Feng,Tian Xiaohua,et al.Data gathering with compressive sensing in wireless sensor networks:A random walk-based approach[J].IEEE Transactions on Parallel and Distributed Systems,2015,26(1):35-44.
[7]王冲,张霞,李鸥.无线传感器网络中基于压缩感知的分簇数据收集算法[J].传感器与微系统,2016,35(1):142-145.
[8]刘冬培,刘衡竹,张波涛.基于准循环双对角阵的LDPC码编码算法[J].国防科技大学学报,2014,36(2):156-160.
[9]Fafianie S,Bodlaender H L,Nederlof J.Speeding up dynamic programming with representative sets:An experimental evaluation of algorithms for steiner tree on tree decompositions[J].Algorithmica,2015,71(3):636-660.
[10]Azad A,BulucA,Pothen A.A parallel tree grafting algorithm for maximum cardinality matching in bipartite graphs[C]∥The 30th IEEE International Parallel&Distributed Processing Symposium (IPDPS),Chicago,USA:IEEE,2015:1231-1241.
[11]Wu Xuangou,Yan Xiong,Yang Panlong,et al.Sparsest random scheduling for compressive data gathering in wireless sensor networks[J].IEEE Transactions on Wireless Communications,2014,13(10):5867-5877.
Compressible data gathering scheme for reliability and energy consumption optimization*
LI Peng,WANG Jian-xin
(School of Information Science and Engineering,Central South University,Changsha 410083,China)
The existing wireless sensor networks(WSNs)data gathering methods cannot be ensure reliability of data gathering with low cost.To solve this problem,Based on the theory of compressive sensing(CS),sparse matrix based on exponential kernel function and measurement matrix based on quasicyclic low density parity check (LDPC)code are designed to be used for data acquisition of node.Maximization of network lifetime is target,the measurement value transmission problem is modeled as the Hamilton loop problem,and a data gathering path optimization algorithm based on tree decomposition is proposed.Simulation results show that the performance of the proposed scheme is better than the typical data gathering methods in terms of data reconstruction error and energy consumption.
wireless sensor networks(WSNs);data gathering;compressive sensing(CS);sparse matrix;measurement matrix;tree decomposition
TP393
A
1000—9787(2016)06—0024—03
10.13873/J.1000—9787(2016)06—0024—03
2016—05—23
国家自然科学基金资助项目(61472449,61173169,61402542)
李鹏(1983-),男,湖南泸溪人,博士研究生,研究方向为无线传感器网络、压缩感知技术。
