触变型流体流变模型的研究进展*

柳建新, 宋勇东, 章　震, 陈　通, 路建光

(1 长江大学石油工程学院，湖北　武汉　430100；2 中油国际(曼格什套)有限责任公司，北京　100000)



触变型流体流变模型的研究进展*

柳建新1, 宋勇东1, 章震1, 陈通1, 路建光2

(1 长江大学石油工程学院，湖北武汉430100；2 中油国际(曼格什套)有限责任公司，北京100000)

从宏观和微观两个方面，对触变型流体的流变模型进行了分类和简要介绍。从宏观机理出发，介绍了连续介质模型，结构动力学模型，化学动力学模型；从微观机理角度出发，介绍了微观结构模型。最后，为了给钻井液等石油领域的触变性流体建立适宜的数学模型，介绍了目前描述钻井液流体模型。

触变性；非牛顿流体；流变模型；结构参数

流体的流动粘度随着外力作用时间的长短逐渐减小的性质即为触变性，亦称摇变性。通常流体的粘度变化与体系内化学性质、物理结构的变化有关，因此发生触变效应时，可以认为液体内部有某种结构遭到破坏，或者认为在外力作用下体系内的某种结构的破坏速率大于其恢复速率[1]。触变型流体为时序性的非牛顿流体，由于其流变性形成机理的复杂性，目前还没有形成比较成熟的理论。在石油工业领域触变型流体有着较广泛的应用，如原油、钻井液、水溶性聚合物溶液等，为准确描述不同油藏条件下流体的流动规律，本文将国内外已有的典型触变性模型进行了整理及分析。

1　流体的流变模型

目前用于描述触变性而建立流体触变学方程的方法不尽相同， 对于某些流变特性复杂的流体材料，可由一般的现象学模型来描述。然而从科学的理论角度出发，需要用流体的微观机理来解释甚至是预测流体的性质。目前已被提出的大量模型只是适用于已经被流变实验测定的特定材料。考虑到流体材料的各异性，目前还没有描述不同材料的通用模型。

寻求流变本构方程的基本方法可分为唯像性法和分子论法[1]。唯像性法一般不考虑材料的微观结构，而是强调实验结果，通过使用线性流体本构方程的研究结果，直接给出描写非线性流体的应力、应变、应变速率间的关系，也可以这样理解：将被研究的流体作为连续介质来处理，采用连续介质的数学方法进行研究，又称宏观流变法；分子论法则重在建立能够描述材料大分子链流动的数学模型，从物质内部结构的角度研究微观结构对材料流动性的影响，分析流体宏观流变特性与流体内部围观、亚微观结构的关系，这种方法又称微观流变法[1-2]。

从宏观角度出发，将流体作为连续介质来处理，一般可分为连续介质模型，结构动力学模型，化学动力学模型这三类模型。

1.1连续介质模型

连续介质模型以连续介质基理为准则，导出本构方程。比较典型的是Slibar and Paslay的模型[3]：

(1)

(2)

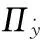
此模型考虑了屈服应力和各向异性，可被用于线性粘弹性模型。并且该模型还可通过实验作出瞬时曲线与其进行比较，但是需首先假定流体具有屈服特性，所能应用的材料范围较小。

White and collaborators[4-5]修改了式(1)，引入了粘弹性压力变量：

(3)

(4)

式中：G为Maxwell模数，τ为松弛时间，s为时间，c-1(t′,t)为Finger应变张量。

对于式(3)和式(4)其屈服应力和初始屈服应力可由下式给出：

(5)

(6)

该模型能很好地描述炭黑填充橡胶材料[4]。

1.2结构动力学模型

此类模型的剪切历史效应大多数是通过与结构参数相关的动能或演化方程来表述的，所以此类模型的流变参数大多数都是结构参数λ的函数。结构参数描述的是材料的瞬时结构。

适用于无弹性触变性材料的模型可以归纳成以下的一般形式[3]：

(7)

(8)

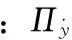
一维无弹性触变性流体本构方程一般形式：

(9)

式中：ηλ=0为即流体内部结构完全破坏时的粘度，ηλ为结构对粘度的贡献度，σy为屈服应力，ηλ随着结构参数λ的变化而改变[3]。表一为不同学者对式(9)的表达，可以参照表1，再结合自己的需要做调整。此类模型经过调整后，可用于高剪切速率下流体流变参数的计算。

表1　屈服应力、结构粘度与结构参数的关系[3]Table 1　Some relations between rheological parameters and the structure parameter[3]

注：γc为弹性力，可以是常量也可以是变量。

早期的模型没有把屈服应力设为常量，但很明显这种模型有一定缺陷。在所有的模型中，屈服应力只有在结构完全破坏时等于零，屈服应力为零表示在某个结构状态下，屈服应力完全消失了。模型预测了每个结构参数λ≠0时刻的屈服应力，屈服应力会随着结构参数的减小而减小，并且当剪切力与屈服应力相等时，剪切速率范围会变小，故带屈服应力的模型不能用来描述流动状态在低结构等级时的情况(λ较小时的情况)。

对于等式(9)，弹性只能通过屈服应力来引入。而在许多触变性模型[6-8]中，其弹性的引入运用了Maxwell模型。这类模型的一维形式为：

(10)

式中：ηM为Maxwell粘度，GM为Maxwell模数。Maxwell模数代表的不是屈服应力，而是一个有限的高频模数。它常被当作常量或者是关于结构参数的线性函数。等式(10)不能描述剪切速率突然下降时剪切力的变化，它还缺少屈服应力，这与实际情况有差别。此类模型可用于高分子基质的触变性悬浮液，如不饱和聚酯，前提是要运用非线性广义Maxwell模型[9-13]。

1.3化学动力学模型

化学动力学模型的一般形式是根据化学动力学机理推导而出的，胶体关于结构变化的基本化学机理有以下四个要点[14]。

(1)粒子或者絮体之间链结的形成原因是粒子的热运动和吸引力，例如：异向移动聚合，即与布朗运动相关的聚合；

(2)粒子或者絮体之间链结形成的原因是对流运动，例如同向移动聚合；

(3)由热运动引起的链结破坏；

(4)由流动引发的链结破坏。

这类模型可以被归纳成以下的一般形式：

(11)

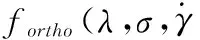
表2　化学动力学方程的不同表达形式[3]Table 2　Expressions for the terms of the kinetic equation[3]

注：表中k1、k2、k3为链结破坏和形成的速率常数，a、b、c、d、β为与材料相关的参数，这些参数可以自行根据材料性质调整。

然而，并不是所有的化学动力学方程都能归纳成式(11)的形式。在这类方程[15-19]中，稳态λ的值，一般遵循聚集与分解的平衡过程。由于λss与结构之间的距离有关，一些学者用稳态值λss来表示结构参数的变化速率。其一般形式如下：

(12)

等式(12)经常被运用于结构未完全破坏或者结构破坏为完全不可逆的过程。

1.4微观结构模型

微观结构模型是从流体的微观结构角度出发，建立其本构方程。其主要特点在于首先抓住高分子材料是由一些长度不同的链组成，每根链又由一系列单体单元构成的事实，研究分子链的结构细节，分子链构象及运动特性对材料流变性质的影响，从而阐明材料在链段和分子链层次的结构参数与材料流变特性的内在联系。

Cross[20]模型：

(13)

式中：N为大分子的平均链结数目，k2是与布朗运动相关的速率常数，k0、k1为布朗运动和剪切引起的链的破坏的速率常数,P表示单粒子单位体积，m为决定胶凝结构的变化速率的常量。

Lapasin用分形方法描述了絮凝悬浮液[20]。基于簇簇凝聚机理，运用计算机模拟计算，结果表明Quemada模型中的Cfp可以用下式表示：

(14)

(15)

式中：A、B是常量，Nmax是悬浮物中基本粒子的数量，β=3/D-1，D是悬浮物的分形维数，Nmax,∞是Nmax的下限值，a,b,p是材料常数。

2　常用一维模型及在钻井液方面的应用

钻井液是一种在井筒中流动的典型触变性流体，它承担了携带钻屑、平衡地层压力、冷却钻具和传递水动力等功能，其流变特性对其性能有着十分重要的影响。钻井液在井筒中的流动过程可以简化成一维流动的形式，常见的一维形式的流体流变模型有以下几种。

Morre[21]的模型:

状态方程为：

(16)

速率方程为：

(17)

式中：λ为描述流体内部结构的参数，结构完整是λ=1；结构完全破坏时λ=0；μ∞为结构完全破坏后的液体粘度；a,b分别为结构恢复和破坏时的速率系数；c为比例系数。Morre提出的触变模型用于描述不具有屈服值的流体。

Cross模型：

(18)

(19)

此模型的状态方程与Morre模型的状态方程相同，但速率方程不同，该模型认为结构破坏速度是剪切速率的幂函数[22]。

Worrall-Tuiliani模型：

(20)

(21)

该模型与Morre模型的区别在于：在状态方程中增加了屈服应力项，可适用于具有屈服应力的触变性流体[23]。

Worrall-Tuliani-Cross模型：

(22)

(23)

该模型为Worrall-Tuiliani模型与Cross模型的结合，集合了两个模型的优点。

Cheng模型：

(24)

τy=τy0+λτy1

(25)

(26)

式中：τy0为结构完全破坏时的屈服应力；τy1为结构完全恢复时屈服应力的增量；a为结构建立常数，b为结构破坏常数。

Cheng-Evabs广义模型：

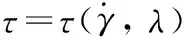
(27)

(28)

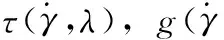
Houska模型：

(29)

(30)

式中：τy0、τy1、K、ΔK、n均为物性常数，被认为只与温度有关；a为结构建立常数；b为结构破坏系数；m为决定胶凝结构的变化速率的常量。Houska认为触变性应归咎屈服值和结构稠度同时降低的结果，且两者的破坏速率是一致的[26]。

基于现场应用便利的考虑，钻井液的常用模型[27]有宾汉模型，幂律模型，赫巴模型，卡森模型等较为简洁的形式，主要有以下几种流变模型。

宾汉模型：

τ=τy+ηpγ

(31)

幂律模型：

τ=Kγn

(32)

赫巴模型：

τ=τy+Kγn

(33)

卡森模型：

(34)

其中，τ为切应力；τy为屈服应力；ηp为结构粘度，γ为剪切速率，K稠度系数，η为视粘度，η∞为卡森粘度。

但以上流变模型仅反映了流体的剪切稀释特性，未引入反映流体内部结构恢复及破坏速率的参数，因此尚无法描述钻井液的触变性。考虑到目前钻井液流变性的测量方法，对钻井液流变模型的改进可参照结构动力学模型，根据应用的需求，如是否要求对屈服应力的描述，屈服应力满足怎样的关系等，对已有的模型进行完善。

3　结论与建议

(1)触变性流体目前主要有连续介质模型、结构动力学模型、化学动力学模型和微观结构模型几种数学模型。但已有的这些模型及其参数一般只适用于特定的材料，目前尚无比较统一的、能够描述各种触变材料的触变模型，而且仍难以构建符合实际触变特性的数学模型。

(2)触变性流体是具有时间依赖性的非牛顿流体，不同学者对触变性流体结构和时间依赖性的的理解也不尽相同。因此这些流变模型关于对建立剪切历史与微观结构之间的联系仍然存在着各种缺陷。

(3)目前大部分钻井液流变模型仍难以反映其真实的触变特性，因此对目前常用钻井液流变模型的改进显得尤为重要，考虑到目前钻井液流变性的测量方法，对钻井液流变模型的改进可参照结构动力学模型进行。

[1]吴其晔,巫静安.高分子流变学[M].北京:高等教育出版社,2002:73-103.

[2]祝连庆.生物流变特性测试方法及应用研究[D].哈尔滨:哈尔滨工业大学,2013.

[3]Mewis J,Nj W. Thixotropy[J]. Advances in Colloid & Interface Science,2009,147-148(214-227.

[4]Montes S, White J L. Rheological models of rubber-carbon black compounds: low interaction viscoelastic models and high interaction thixotropic-plastic-viscoelastic models[J]. Journal of Non-Newtonian Fluid Mechanics, 1993, 49(2-3): 277-298.

[5]Meins J F o L, Moldenaers P, Mewis J. Suspensions in Polymer Melts. 1. Effect of Particle Size on the Shear Flow Behavior[J]. Industrial & Engineering Chemistry Research, 2002, 41(25): 6297-6304.

[6]Quemada D. Rheological modelling of complex fluids: IV: Thixotropic and[J]. European Physical Journal Applied Physics, 1999, 5(2): 191-207.

[7]Quemada D, Droz R. Blood viscoelasticity and thixotropy from stress formation and relaxation measurements: a unified model[J]. Biorheology, 1983, 20(5): 635-651.

[8]Coussot P, Leonov A I, Piau J M. Rheology of concentrated dispersed systems in a low molecular weight matrix[J]. Journal of Non-Newtonian Fluid Mechanics, 1993, 46(2-3): 179-217.

[9]Isayev A I, Fan X. Viscoelastic plastic constitutive equation for flow of particle filled polymers[J]. Journal of Rheology, 1990, 34(1): 35-54.

[10]Leonov A I. On the rheology of filled polymers[J]. Journal of Rheology (1978-present), 1990, 34(7): 1039-1068.

[11]Letwimolnun W, Vergnes B. Stress overshoots of organoclay nanocomposites in transient shear flow[J]. Journal of Non-Newtonian Fluid Mechanics, 2007, 141(167-179.

[12]Simhambhatla M, Leonov A I. On the rheological modeling of viscoelastic polymer liquids with stable constitutive equations[J]. Rheologica Acta, 1995, 34(3): 259-273.

[13]Sobhanie M, Isayev A I, Fan Y. Viscoelastic plastic rheological model for particle filled polymer melts[J]. Rheologica Acta, 1997, 36(1): 66-81.

[14]Goodeve C F. A general theory of thixotropy and viscosity[J]. Trans Faraday Soc, 1939, 35(1): 342-358.

[15]Suetsugu Y, White J L. A theory of thixotropic plastic viscoelastic fluids with a time-dependent yield surface and its comparison to transient and steady state experiments on small particle filled polymer melts[J]. Journal of Non-Newtonian Fluid Mechanics, 1984, 14(3): 121-140.

[16]LIU T Y, SOONG D S, KEE D D. A MODEL FOR STRUCTURED FLUIDS[J]. Chemical Engineering Communications, 1983, 22(5): 273-286.

[17]Nguyen Q. Thixotropic behaviour of concentrated bauxite residue suspensions[J]. Rheologica Acta, 1985, 24(4): 427-437.

[18]Petrellis N C, Flumerfelt R W. Rheological behavior of shear degradable oils: Kinetic and equilibrium properties[J]. Canadian Journal of Chemical Engineering, 1973, 51(3): 291-301.

[19]Tiu C, Boger D V. COMPLETE RHEOLOGICAL CHARACTERIZATION OF TIME-DEPENDENT FOOD PRODUCTS[J]. Journal of Texture Studies, 2007, 5(3): 329-338.

[20]Barnes H. Thixotropy-A review[J]. Journal of Non-newtonian Fluid Mechanics, 1997, 70(1): 1-33.

[21]李平.低速梯下钻井液流变性和触变性研究[D]. 成都:西南石油大学,2009.

[22]Kane M, Djabourov M, J-L V, et al. Morphology of paraffin crystals in waxy crude oils cooled in quiescent conditions and under flow[J]. Fuel, 2003, 82(2):127-135(129).

[23]Ritter R A, Govier G W. The development and evaluation of a theory of thixotropic behavior[J]. Canadian Journal of Chemical Engineering, 1970, 48(5):505-513.

[24]Cheng-H D C. Thixotropy[J]. International Journal of Cosmetic Science, 1987,9(4): 151-191.

[25]Cheng C H. Yield stress: A time-dependent property and how to measure it[J]. Rheologica Acta, 1986, 25(5): 542-554.

[26]Sifferman T R. Flow Properties of Difficult-To-Handle Waxy Crude Oils[J]. Journal of Petroleum Technology, 1979, 31(8): 1042-1050.

[27]Livescu S. Mathematical modeling of thixotropic drilling mud and crude oil flow in wells and pipelines—A review[J]. Journal of Petroleum Science & Engineering, 2012, 98-99:174-184.

Research Progress on Rheological Model for Thixotropic Fluid*

LIU Jian-xin1, SONG Yong-dong1, ZHANG Zhen1, CHEN Tong1, LU Jian-guang2

(1 College of Petroleum Engineering, Yangtze University, Hubei Wuhan 430100;2PetroChinaInternational(Mangistau)CompanyLtd.,Beijing100000,China)

From the view of macrography and micrography, the rheological model for thixotropic fluid was classified and introduced. From a macro perspective, there were continuum mechanics models, structural kinetics models and chemical kinetics models. From the micro perspective, there was a model which was built considering its microstructure. Finally, the common model used in the drilling fluid was discussed.

thixotropy; non-newtonian fluid; rheological model; structure parameter

湖北省高等学校大学生创新训练项目(No.104892014039)。

柳建新(1974-)，男，博士，讲师，现主要从事油气田化学方面的研究工作。

O373

A

1001-9677(2016)013-0009-04