基于模糊不确定需求条件下疏散计划优化方法的研究
2016-09-01曾赛峰张益星高德翔
李 峰,曾赛峰,张益星,高德翔
(湖南工程学院 计算机与通信学院,湘潭 411104 )
基于模糊不确定需求条件下疏散计划优化方法的研究
李峰,曾赛峰,张益星,高德翔
(湖南工程学院 计算机与通信学院,湘潭 411104 )
疏散计划是灾害管理的一项重要的内容.针对疏散计划固有的不确定特性,提出了一种公共交通疏散路线设计.设计中,每个受灾点灾民的需求用模糊数据表示,车辆线路的分配用置信指数表示,通过实验分析和讨论了最后结果中不确定因素对疏散计划的不利影响,评估了置信偏好指数对设置线路的影响,设计了解决疏散计划的最佳方案,并获取了最佳参数.
疏散计划;模糊不确定需求;优化;路线设计
0 引 言
最近发生在城市地区的灾害(如地震、洪水、飓风、化学品泄漏、核事故)凸显应急管理的重要性.虽然灾难发生的概率相对较低,但其悲剧性的后果使得人们在它们发生之前就应该有所防备.
紧急疏散是一个重大的战略性应急管理计划.通过紧急疏散人们从危险区域移到的安全区域,减少了损失.在疏散行动中,一些人可能会使用私家车自行疏散,但是还有一些人没有私家车是不能自行疏散的.这些人群主要包括青少年,老人、残疾人、游客或低收入居民,他们只得依靠公共交通疏散.
公共交通系统在提高疏散效率中发挥着至关重要的作用[1,2,3,4].Naghawi和Wolshon[5]认为公交巴士能够增加疏散人口的总数并最小限度地减少对疏散路线交通的影响.陈、周[11]认为有条理的逃生时间安排可大大提高疏散效率.因此疏散计划应该计划周全,以提高应急管理水平.
疏散规划是复杂的而且具有挑战性的问题,因为在紧急情况下留给决策者的信息是不确定性的.在使用公共交通进行疏散时,疏散人员的信息和他们的及时位置、疏散车辆和交通网络都有可能不确定、不完整甚至错误.车辆的数量,承载力量和位置也可能是不确定的.交通网络中有限的接入容量、行车时间以及有限的网络接入等等造成网络的不确定性.此外,如图1所示的灾难发生时间和其严重性的不可预测性也是疏散计划的不确定性因素.
绝大多数疏散计划很可能忽视不确定性因素.而一个实际疏散操作是难以完全遵循预定的计划的.因此,最优疏散计划应该考虑不确定性因素以保证较高的执行概效率.
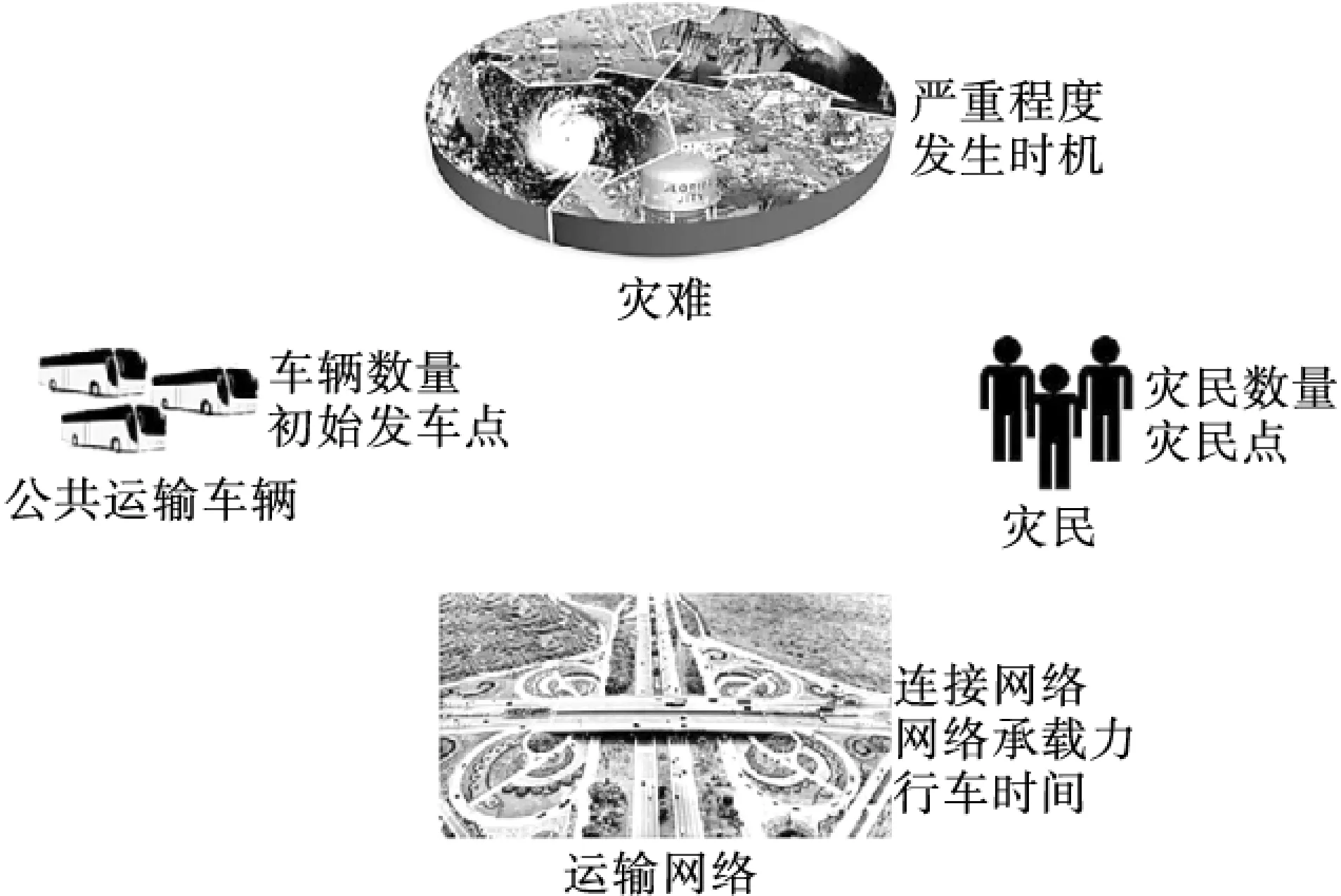
图1 疏散计划中公共交通的不确定因素
本文提出了一种在城市地区使用公共交通工具来疏散车辆的问题(EVRP).在此问题中疏散需求是不确定的.在这里,在每个疏散点的需求(疏散)用模糊变量表示并用模糊置信理论来处理这种不确定性.文中使用随机模拟方法评估解决方案.使用模糊置信理论对行车路线分配尚属首次.
1 模糊置信理论
现实中许多模糊现象不能明确描述.Zadeh[7]引入了模糊集合的数学理论,通过其中的元素能够更好地处理不确定现象.Zadeh使得处理模糊事件变为可能.Liu[6]发现了置信理论,是研究不确定现象一个分支.其中的可能性,必然性和可信度可以描述如下.
定义1:让θ成为非空集合.P(θ)就是其概率集合.其中的每一个元素称为事件,∅是空集.对于每一个A属于P(θ)可以得到非负数Pos(A),其表示事件A发生的概率(公式1).

(1)
三元集合(θ,P(θ),Pos)称为概率空间,函数Pos是概率衡量函数.
定义2:定义三元集合(θ,P(θ),Pos)为概率空间,A是P(θ)的集合.A必定发生概率由公式2定义.其中AC是A的互补事件.
Nec{A}=1-Pos{AC}
(2)
定义3:定义三元集合(θ,P(θ),Pos)为概率空间,A是P(θ)的集合.则A的可信度函数可以描述如下:
(3)
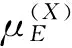
(4)
正如所描述的,模糊事件的可信度等于其可能发生和必定发生的平均值.假如可信度为1,模糊事件一定发生;若为0,则一定不发生.
2 详细方法
这章阐述了技术的细节.在2.1、2.2 、2.3节分别阐述了EVRP模型.该模型描述了模糊置信理论并用GA[8]模型解决EVRP问题.
2.1模型描述
本文模拟了城市公共交通疏散计划.计划中人们在候车区等待公共车辆的到来.这里传统的公交车站被设置为候车区.受灾群众被转运到附近的避难所.假设有充足的车辆提供输送.
疏散问题常建模在行车线路问题上.在经典版本的VRP[9],问题的目的是设计出一整套线路,如图2所示车辆按照行车线路能够从停车点穿过所有受灾点提供服务,最后重返停车点.线路设计要求耗费最少.这里的耗费用行车距离和行车时间衡量.
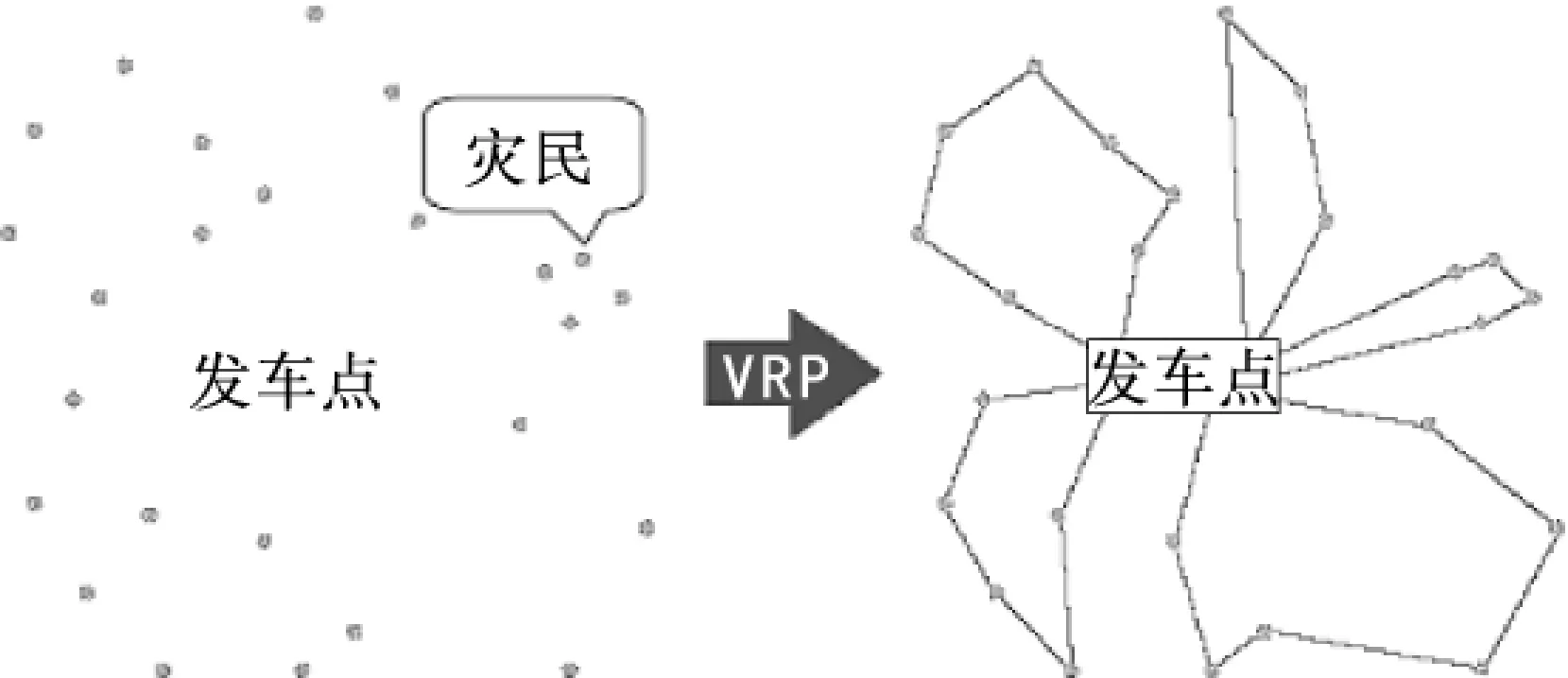
图2 经典车辆行车线路(VRP)
本文中VRP被扩展到EVRP.在EVRP中,每一部车从停车点开始穿过每个受灾点,运送灾民,当车满了会疏散到最近的避难所,如图3所示.这里灾民点的位置设计应尽量使行车花费时间最少.这样可以减少救援时间.整个救援时间由运输网络模型计算.
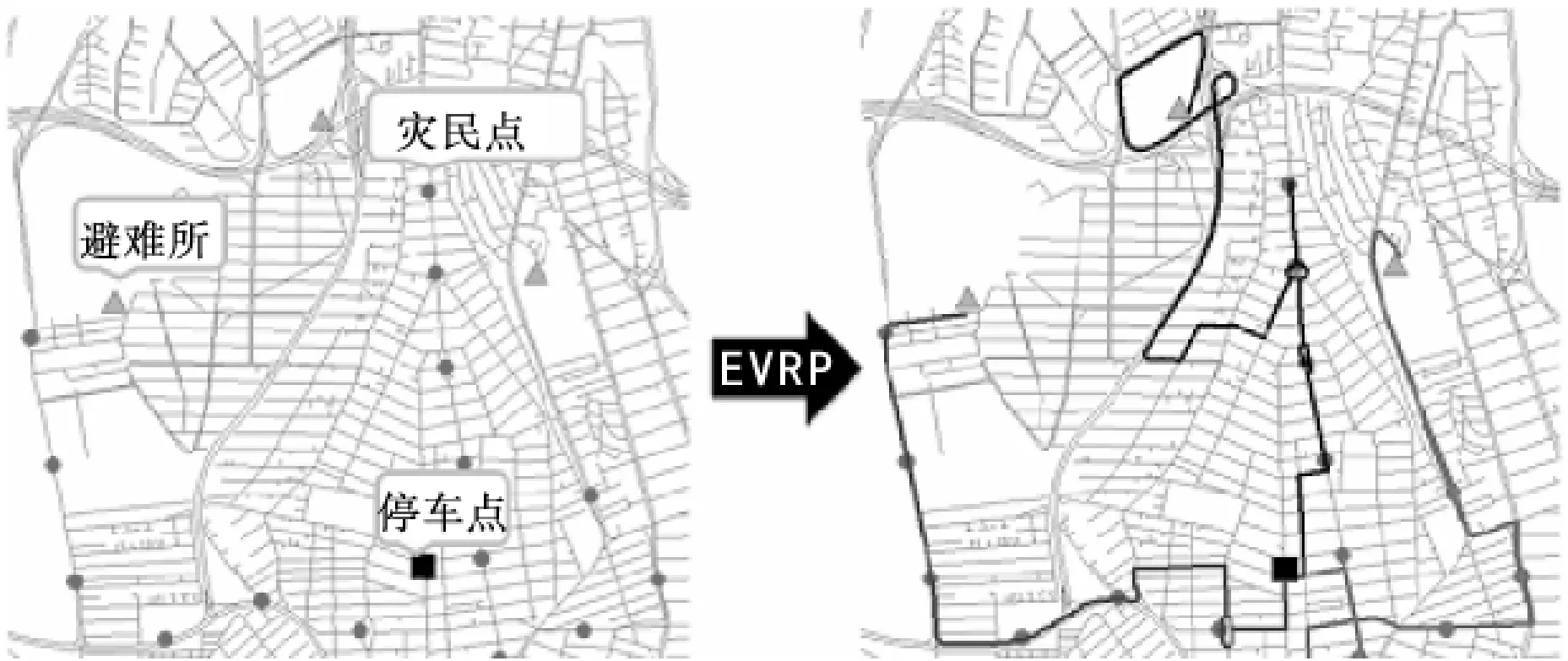
图3 疏散车辆路径问题(EVRP)
在EVRP中假定车辆都有相同的承载量,当它们开始出发时都是空车.
EVRP的数学公式描述如下.问题用图描述.在图中,N和E分别表示边和节点.
节点是停车点、受灾点和避难所的集合.边是在节点和运送网络之间的最短路径.在接下来的数学描述中,我们用到了节点的子集合.为了便于理解,变量的注释在图4给出.

图4各变量含义
2.2EVRP模糊置信理论
为了处理逃生过程中的不确定性,一个三维模糊变量被用来评估受灾点的灾民人数.
防灾抗灾指挥人员可以凭借他们的经验、直觉或历史数据估计出受灾人数不会少于e1或大于e3.e2介于两者之间,可以人为评估如图5所示.
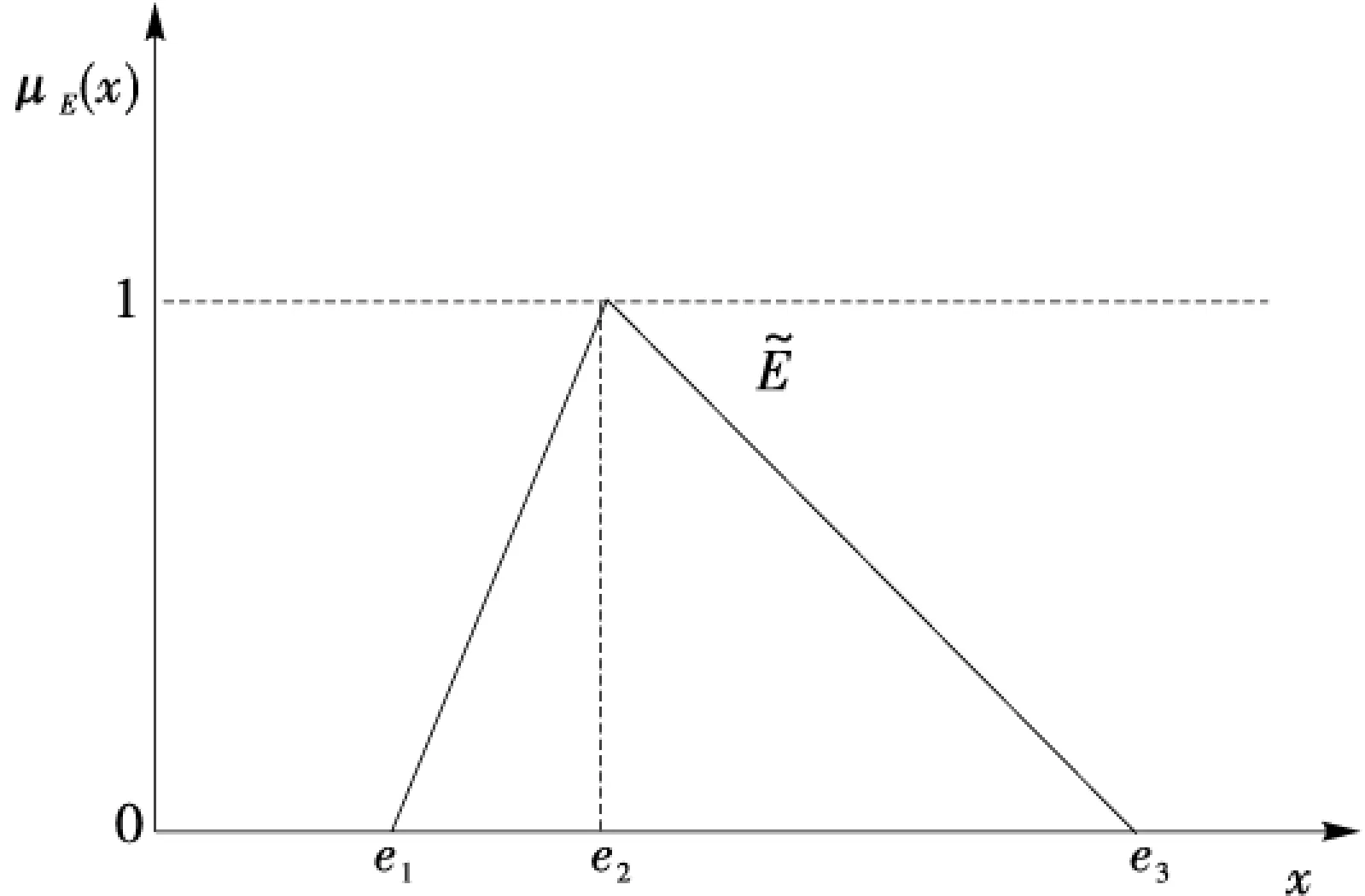
图5 用来评估灾民数量的三维模糊变量
根据基本定义模糊变量E发生的可能性、必然性和可信度可以描述为公式(5)-(7).
(5)
(6)
(7)
救灾时车辆是否能顺利从一个受灾点行走到另一个在于它的承载能力和灾民的数量.若车辆的承载力大于等于下一个受灾点的灾民.该车辆可以根据其预设路径驶向受灾点运送灾民.否则其应该驶离到附近避难所.
若灾民数量确定,容易决定车辆是驶向下一个受灾点还是驶离到附近避难所.但是,当灾民人数变量用三维模糊变量描述时,救灾的决策就会很复杂.下一个受灾点的灾民数量比车辆的承载量相比越少,车辆驶向下一个受灾点的可能性也就越大.
在驶离第m个受灾点后车辆k的承载能力可以描述如公式(8).
(8)
此处C是车辆的初始承载能力,ei表示在受灾点i的灾民数量.
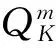
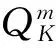
(9)
根据公式(7)-(9),衡量车辆在下一个运点的承载量可以描述为公式如下.
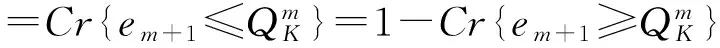
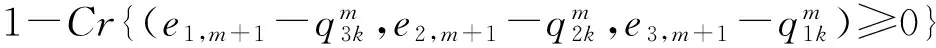
Cr的值表示车辆驶向下一个节点的概率.当其值1,表示车辆应该驶向节点,若为0则车辆不能驶向下一个受灾点而应该驶离到附近避难所.
若基于Cr作决定,应该考虑Cr的值.若Cr>-Cr,车辆应该驶向灾区,低值Cr表示可以尽可能使用车辆的承载力,但也很可能表示到达下个灾区时车辆无法承载该灾区所有灾民.
而高值Cr可以通过大量地增加路线的数量减少失败的概率.
2.3Cr参数的优化
逃生路径可以基于难民的数量模糊估计而设计.实际中车辆按照计划线路行驶,但承载的是实际的难民人数.
实际中若因为车辆有限的承载力而不能走遍所有受灾区时,它应该驶离到最近的避难所,放下车上所有灾民,重新回到受灾区运送灾民.
如图6所示,车辆由于运送的失败,不得不占用额外的运送时间,从而增加了总时间的开销.
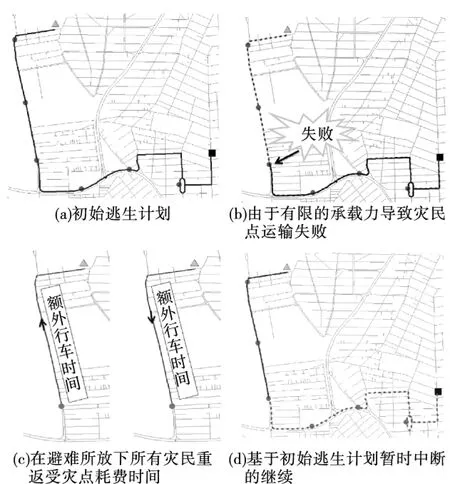
图6 逃生路径状况图
Cr的值极大地影响了失败的次数和额外运送时间.因此我们应该用最少的运送时间来决策逃生计划.
为了选择一个最优参数,本文用在0~1之间变化的Cr值来测试EVRP.然后对所有生成的路径进行评估.首先每个受灾点确切的灾民数量应该知道.但实际上我们只知道模糊数量.为了解决这个问题,我们引入了随机仿真方法来模拟每一个受灾点确切的灾民数量.
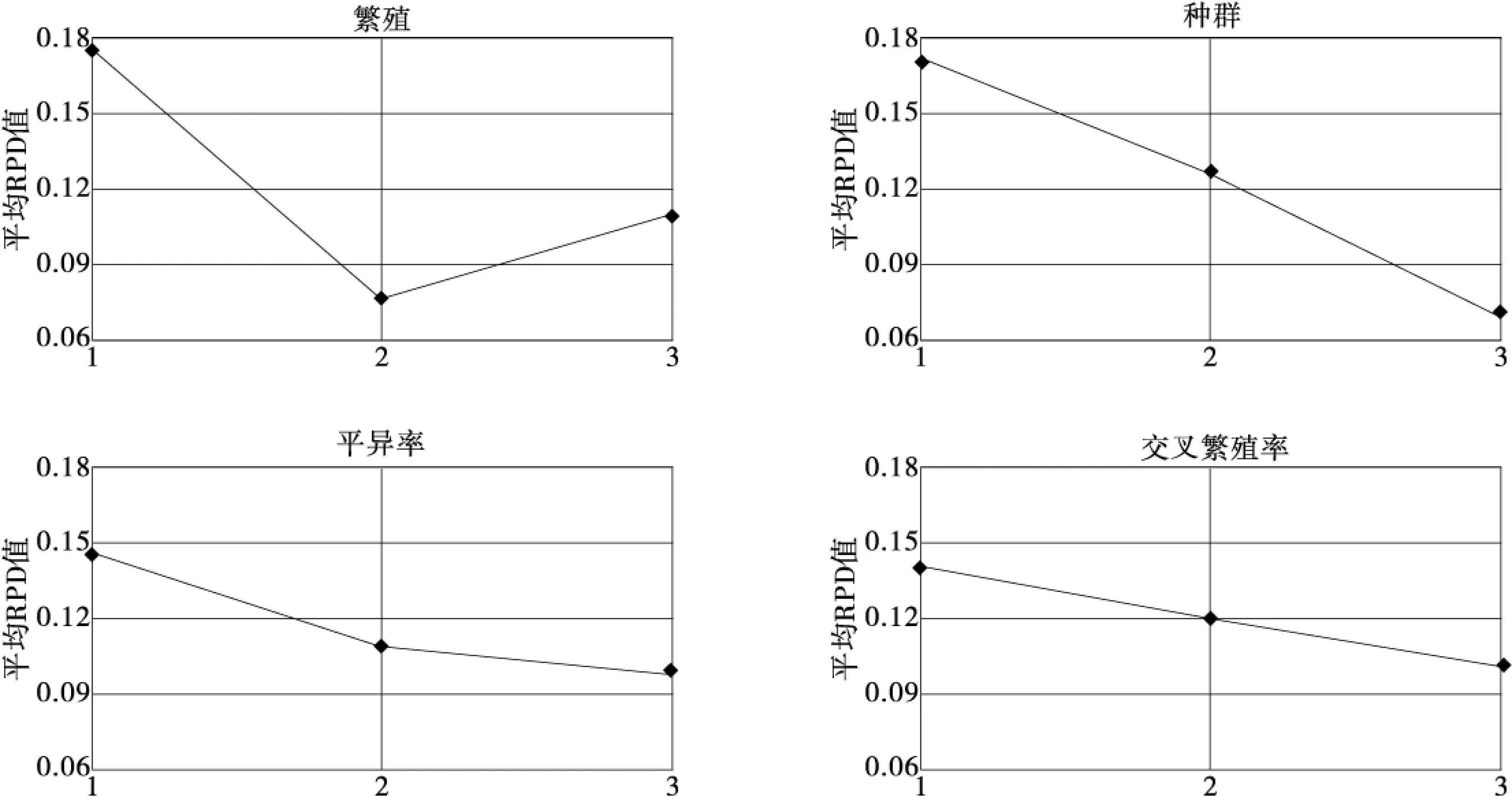
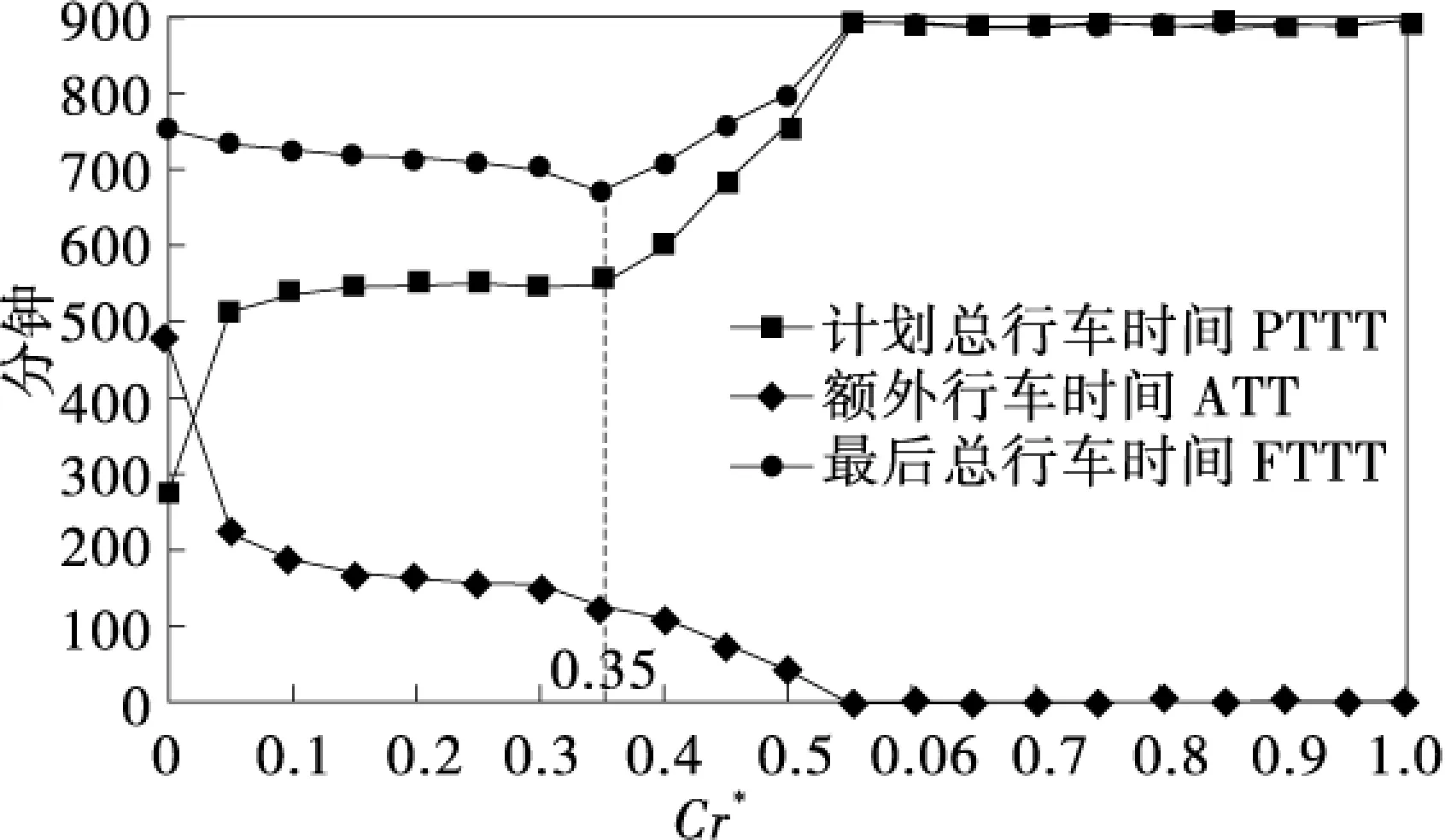
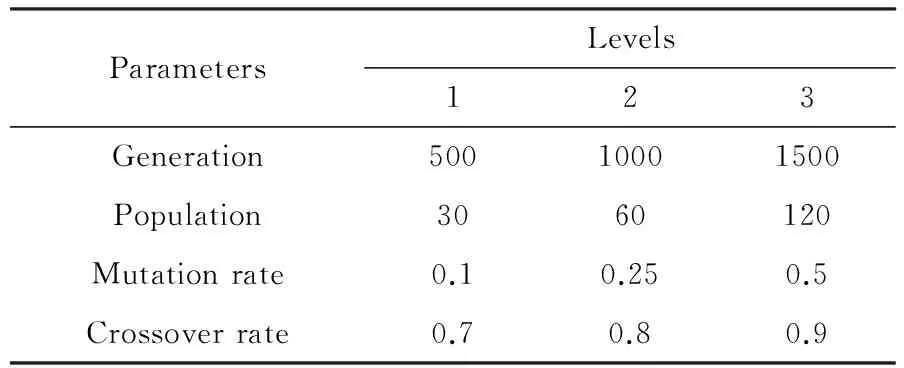
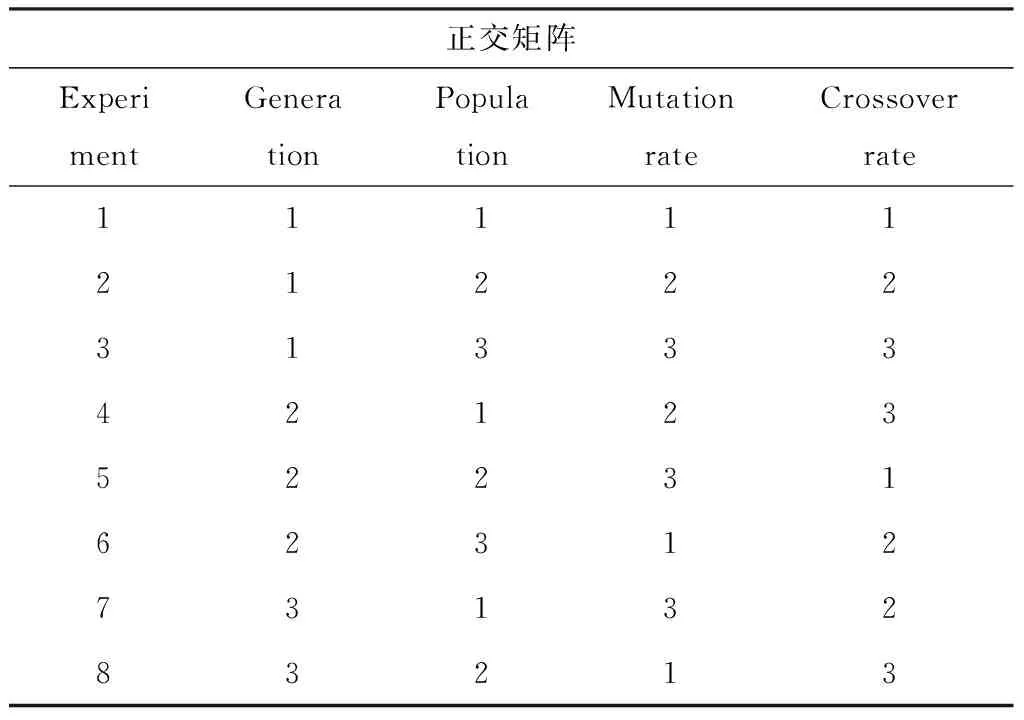
对每一个受灾点i,我们在ei1和ei2之间取值d并以此计算模糊成员函数.因此产生随机变量r.当r 在仿真了灾民实际数量后,通过比较每个受灾点的灾民的累加数量和车辆的承载能力可以计算出额外时间开销.最后,由Cr值计算出整个运输时间. 随机仿真逃生路线可以重复实验M次.计算出结果的平均值来确定相应指数Cr. 2.4经典解决方案 算法中每一个完全方案都由一串数字编码.每一个数字表示一个受灾点.插入虚设的零值表示每条独立的行车路径.例如 图7表示能同时处理4辆车和10个受灾点的方法.每一条行车路径从发车点开始到最近的避难所结束. 每种方案都需要简单的定位.这种定位不包括车辆行进路线的预先规划,而且由虚设的零值分割. 图7 经典方案 2.5初始化人口 初始化人口的数量就是方案中PopSize值. Taguchi用健壮参数设置方法优化了GA模型的参数[10].Taguchi实验中的质量驱动方法对优化线路设计的性能、质量、耗费不失是一种高效系统的方法. 设计算法参数也就是设计不同优化级别的参数.因此算法对于外部干扰很健壮.但是通过实验确定微小的参数耗费巨大.Taguchi实验可以减少实验的次数,获得近似的优化参数集合.实验简化了数组,重点研究在少量试验中产生的大量参数.实验提供了信噪比来衡量算法质量并确定优化参数. 1 setp//灾民点数量 C//车辆承载力,Cr*//可信指数 2X←Smax 3k,i=1 4Vehicle(1)←X1 6Whilei 10ifCr≥Cr*do 11Vehicle(k)←Xi+1 12Else 13k=k+1 14Vehicle(k)←Xi+1 16EndIf 17i=i+1 18EndWhile 图8构建函数的过程 简而言之,信噪比就是平均信号和标准信号的比例.信噪比的标准不同,但表示方式一致.信噪比越大越好. 3.1选择参数和适合级别 GA参数包括:繁殖、种群、突变、杂交,这些都极大影响了算法的健壮性.根据作者经验和相关文献类似问题,对于每个参数都能有3种级别.如表1所示. 表1 GA参数的级别 3.2选择合适的正交矩阵 应该做的实验数量接近于LP,这里L和P分别表示级别和参数.实验需要重复81次才能获得GA参数,这样既费时又费钱.因此,Taguchi方法转而寻找合适的正交矩阵来解决这个问题.据文献[1]合适的正交矩阵由九个参数构成,如表2所示. 表2 正交矩阵 3.3运行实验 Taguchi实验参数L9在表2给出.GA在装有MATLAB的戴尔个人电脑下运行.结果用相对偏移百分比(RPD)来衡量.RPD是平均值,可以缩小结果取值范围. RPDS在相应参数下比例的平均值在图9中表示.考虑RPD的在不同参数下的变化,遗传代和种群对于计算结果有很大的影响. RPD越小,就越接近最佳算法.在此基础上每个优化参数在表3中给出. 表3 GA参数的优化级别 我们使用了优化后的GA.参数Cr在0~1之间变化,每次变化步长为0.05.对于每一个Cr值,GA都运行三遍以获得总的行车时间和逃生时间.为了对计划路线进行评估,对额外行车时间随机仿真重复计算了20遍.计划总行车时间由灾民的模糊数量决定;额外行车时间由随机仿真程序获得的灾民数量决定.最终总行车时间=计划时间+额外时间. 图9 在不同参数下GA对应的RPDs均值 当分配偏好指数Cr变化时,图10表示PTTT、 ATT和FTTT随之变化的曲线图.根据图10,PTTT随着Cr值增大而增大,同时ATT降低. 图10 行车时间随Cr*变量改变曲线 Cr值越低,ATT值越高,PTTT值越低.相反Cr值越高,ATT值越低,PTTT值越高.如图10所示,Cr小于0.35时PTTT的增长率与ATT的下降率成反比.但是,当Cr大于0.35,PTTT的增长率超过ATT的下降率.因此当Cr从0.35增长到1时FTTT也随着增长. [1] M.A . Schwartz, T.A . Litman, Evacuation Station: the Use of Public Transportation in Emergency Management Planning[J]. Inst. Transp. Eng., 2008, 78(1):69-73. [2] Transporatation Research Board (TRB). The Role of Transit in Emergency Evacuation: Special report 294, Committee on the Role of Public Transportation in Emergency Evacuation[R]. Washington, DC, 2008. [3] F. Sayyady, S. Ek sioglu. Optimizing the Use of Public Transit System During no Notice Evacuation of Urban Areas, Comput[J]. Ind. Eng. 2012, 59: 488-495. [4] E.I. Kaisar, L. Hess, A . Benazir. An Emergency Evacuation Planning Model for Special Needs Populations Using Public Transit Systems[J]. Public Transp, 2012, 15(2):45-68. [5] H. Naghawi, B. Wolshon. Performance of Traffic Networks During Multimodal Evacuations: Simulation-Based Assessment[J]. Nat. Hazard. Rev, 2012, 13(3): 196-204. [6] B. Liu. A Survey of Credibility Theory, Fuzzy Optim[J]. Decis. Mak, 2014(5): 387-408. [7] L.A . Zadeh. Fuzzy Sets, Inf. Control[J]. 1965, 8: 338-353. [8] G. Taguchi. Introduction to Quality Engineering, Asian Product[R]. Organ./UNIPUBWhite Plains, 2013. [9] G.B. Dantzig, J.H. Ramser. The Truck Dispatching Problem[J]. Manag. Sci., 2012, 6(1): 80-91. [10] G. Taguchi. Introduction to Quality Engineering, Asian Product[R]. Organ./UNIPUB,White Plains, 2011. [11] C. Chen, C. Chou. Modeling and Performance Assessment of a Transit-Based Evacuation Plan Within A Contra-Flow Simulation Environment, Transp[J]. Res. Rec.: J. Transp. Res. Board, 2009(2): 40-50. Study on Optimization of an Evacuation Plan with Uncertain Demands LI Feng, ZENG Sai-feng, ZHANG Yi-xing, GAO De-xiang (College of Computer and Communication,Hunan Institute of Engineering, Xiangtan 411104, China) Evacuation planning is an important activity in disaster management. Due to the sudden occurrence of disasters, evacuation should be preplanned. It is necessary for evacuation plan to be as close as possible to a real evacuation operation. However, evacuation planning is a challenge because of inherent uncertainty in required information. One important source of uncertainty in evacuation is the uncertainty in evacuation demands. This paper presents an evacuation vehicle routing problem to design evacuation routes for public vehicles. In this problem, demand (number of evacuees) at each pick-up point is introduced as a fuzzy number and the assignment of the pick-up points to the vehicle routes happens based on a credibility preference index. A genetic algorithm based on fuzzy credibility theory is designed to optimize the problem. The optimum parameter set for genetic algorithm is obtained by Taguchi experimental design. The presented problem and algorithm are applied to a part of Tehran transportation network. The impact of credibility preference index on the achieved solutions is evaluated and its best value is determined for the case study. Moreover, different tests are implemented to analyze and discuss the influence of uncertainty level on the final results. evacuation planning;uncertainty level;vehicle routes;optimization 2016-04-08 湖南工程学院青年重点项目(XJ1504);湖南工程学院校级大学生创新项目[校办字83号文件47号]. 李峰(1975-),男,硕士,讲师,研究方向:计算机应用技术. U491.1 A 1671-119X(2016)03-0049-07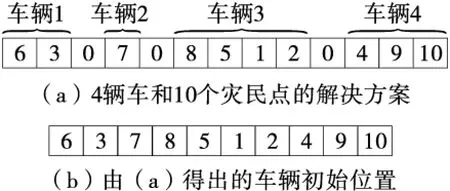
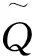
3 Taguchi试验设计
4 试验结果与分析

5 结果和探讨