小型水平轴风力机叶片气动性能优化

李建华,魏克湘,王高升

(1. 湖南工程学院 机械工程学院，湘潭 411101；2. 湖南工程学院 湖南省风电装备与电能变换协同创新中心，湘潭 411101)



小型水平轴风力机叶片气动性能优化

李建华1,2,魏克湘1,王高升1

(1. 湖南工程学院 机械工程学院，湘潭 411101；2. 湖南工程学院 湖南省风电装备与电能变换协同创新中心，湘潭 411101)

小型水平轴风力机叶片气动性能决定着发电机自身的运行寿命与工作效率.风力机叶片翼型的气动性能决定了风力发电机组的功率及载荷特性.为了提高风力机叶片气动性能和减小启动时间，以小型水平轴风力机为例，对比分析翼型对其气动性能的影响，并结合微型多目标遗传算法对弦长、半径和扭角等叶素结构参数进行优化，能高效率地解决功率系数和启动时间等优化问题.

小型风力发电机；气动性能；翼型；微型多目标遗传算法

0　前　言

风能的利用形式主要是以风能作动力和风力发电两种形式，其中又以风力发电为主.风力发电是目前最具规模化开发条件和商业化发展前景的可再生能源发电方式.风轮将风的动能转换为机械能，是风力机的核心部件；风轮由叶片和轮毂组成，其中叶片决定了风能的转换效率，是风轮的关键部件.为了达到最佳气动性能，叶片具有复杂的气动外形，其截面形状复杂，并且在翼展方向存在扭角和渐缩的弦长，构成了复杂的扭曲曲面.这使得叶片设计理论深刻、步骤繁琐、计算量大.叶片的直径、弦长、各截面翼型选择、纵向的扭角分布等都会影响到叶片的气动性能[1-4]，进而影响风轮的功率输出.风力机气动分析与计算是风力机设计和校核中重要的一环.设计出风力机总体参数和叶片气动外形之后，计算其气动性能，其结果可以作为对设计结果的评价；反之，气动性能计算结果可以作为反馈，为修正叶片气动外形提供数据.因此气动性能计算结果的准确度直接影响风力机叶片外形优化设计的优劣.风力机叶片强度、刚度以及稳定性的校核，也有赖于气动计算结果[5,6].本文以两种翼型对比分析水平轴风力机叶片气动性能，并以叶片各截面弦长和扭角为设计变量，采用 MATLAB 软件，基于遗传算法[7,8]实现叶片气动性能优化.

1　叶片气动性能计算的基本方法

叶片气动性能通常以功率系数和推力系数来表示.推力系数CT很大程度影响了塔架的设计，功率系数CP决定了风力机风轮所能获取能量的总量，即反映风力发电机从自然风中捕获风能的能力.

气流流经桨盘时，其速度值会减小，在满足质量守恒、动量守恒和Bernoulli方程的条件下可以推导出叶轮的推力系数和功率系数.叶片气动性能计算的基本方法主要有Glauert法和Wilson法[9,10].Glauert法中不计叶片翼型阻力和叶尖损失的影响但是考虑了风轮后的涡流流动.而Wilson法在此基础上进行了改进，分析了叶尖损失对叶片气动性能的影响.本文在Wilson法基础上进一步改进，引入旋转诱导因子的影响对转矩进行修正.

对于一个具有N个叶片的风力机，作用在某个叶素上的总推力T为：

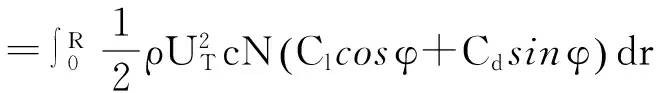
(1)

式中：UT是叶素的总速度，U0是风速，Cl是升力系数，Cd是阻力系数，c是叶素弦长，ρ是空气密度，φ是入流角，α为轴向诱导因子，r为叶素半径.

推力系数为：

(2)

式中：R为风力机半径.

由圆周力引起的转矩为：

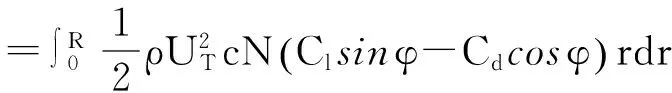
(3)

式中：W2为旋转诱导因子，Q为转矩.

功率系数为：

(4)

式中：P为功率，λr为叶尖速比.

从上式可知与功率系数和推力系数有关的主要是叶素的径向位置，弦长和扭角的几何分布、升力系数和阻力系数.而升力系数和阻力系数依赖于雷诺数和攻角，取决于翼型.在功率系数和推力系数计算的过程，只有给定了轴向诱导因子和旋转诱导因子，入流角φ才能获得，从而升力系数Cl和阻力系数Cd也可以相应求得.这是一个迭代的过程.直到动量和角动量流过叶片的流量和叶素上的推力和转矩达到平衡.

功率系数是反映风力发电机从自然风中吸取风能的能力的评价指标.是风力机叶片气动性能分析中的一个关键系数.

2　小型水平轴风力机叶片多目标优化

2.1优化问题描述

影响风机性能的重要几何参数主要有叶片数、翼型和叶素结构参数(弦长c、半径rad、扭角twi等).获取气动性能良好的翼型和叶素结构参数是叶片建模的基础.小型风力机必须在低风速下快速起动.因此本文以翼型和叶素结构参数(弦长c、半径rad及扭角twi)作为优化变量，以获得良好的功率系数和最低起动时间为优化目标.建立的优化模型如下：

2.2微型遗传算法

微型遗传算法采用小规模种群(一般分布的均匀性，根据个体拥挤距离值进行同一非支配级个体的比较和选择.微型遗传算法的这些优点使其在复杂非线性工程中应用广泛.对叶片气动性能优化问题，功率系数和起动时间与叶片翼型和叶素结构参数间映射关系不是显式函数，需通过复杂计算模型表示，致求解难度加大.遗传算法由于具有基于种群运算的基本特征及可在不考虑问题具体特征前提下用于解搜寻的进化本质，因此非常适合该问题求解.在工程实际中常要依据对问题的了解和决策人员的偏好，从多目标优化问题Pareto 最优解集合中挑选出一个或一些解作为所求多目标优化问题的最优解.遗传算法通过在代与代之间维持由潜在解组成的种群来实现多向性和全局搜索，这种从种群到种群的搜索方法在搜索Pareto 解时是有用的，因此遗传算法是求解多目标优化问题的Pareto 最优解集合的一个有效手段.

2.3叶片气动性能优化过程

叶片气动性能优化过程中涉及到叶素结构(一般沿叶片径向选取10多个剖面，即叶素，每个叶素结构参数主要由半径、弦长和扭角确定)和翼型形状.变量参数过多，难以实现.叶片的翼型在很大程度上决定了风轮的空气动力学性能，所选取的翼型升阻比越高，风力机的效率就越好，而且气动性能曲线与叶片数目及尖速比有关.本文拟假定叶素结构参数不变的情况下，先分析不同翼型对叶片气动性能的影响.选出翼型后，再改变叶素结构参数，优化叶片的气动性能.基于微型遗传算法的叶片性能优化流程如图1所示.

图1叶片多目标优化流程

3　实例分析

以一永磁电机叶片为实例进行分析.已知叶片数为3，最大功率为754 W，材料密度为550 kg/m3，风速为10 m/s，齿槽转矩为0.5 N·m.

3.1翼型对叶片气动性能的影响分析

分析翼型SD7062、翼型NACA4412对本案例叶片的功率、推力、功率系数、推力系数与叶尖速比的关系.由图2和图3可知，翼型SD7062比翼型NACA4412要好.因此本案例选翼型SD7062来构建.

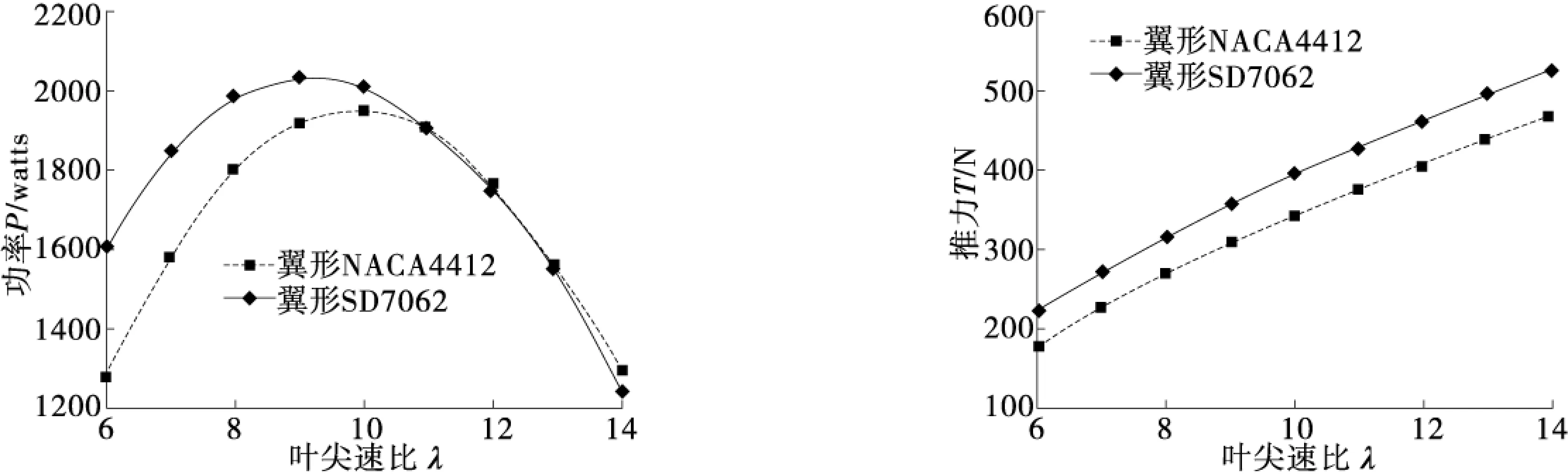
图2　功率和推力与叶尖速比关系

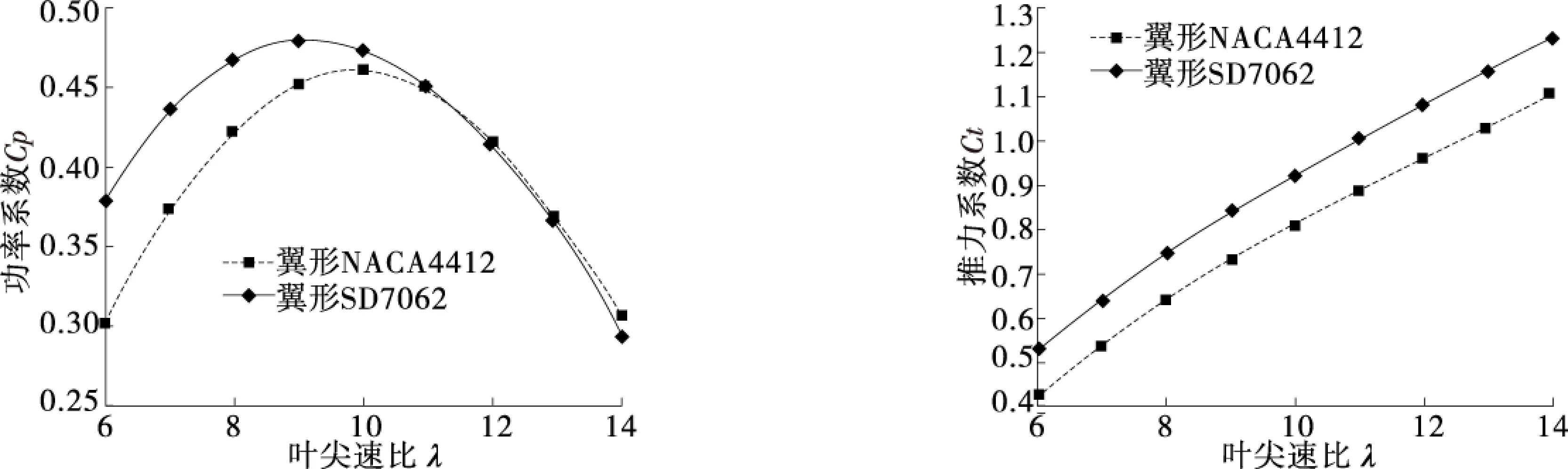
图3　功率系数和推力系数与叶尖速比关系

3.2叶素结构参数优化

选定翼型SD7062后，以叶素的结构参数弦长c、半径rad及扭角twi为优化变量.弦长为[0.03 m,0.2 m]，扭转角为[-5°,25°].叶根半径为1.06 m，轮毂半径为0.125 m.采用微型多目标遗传算法进行小型水平轴风力机叶片气动性能的多目标优化.遗传算法产生设计变量的许多个体，针对每一迭代步的设计变量，可经过足够代数的搜索，在解域内寻找到一系列最优的设计变量组合.由确定的最大代数终止迭代.

微型多目标遗传算法采用的参数设置如下：种群大小=5，交叉概率=0.1，变异概率=0.05，重启动判断代数=5.设计变量采用二进制编码，得到的多目标优化结果(100个非支配解)如图4 所示.由图4可以看出非支配解分布均匀.最小启动时间在1.526～1.838 s之间，最大功率系数则在0.452～0.481之间.表1 列出了从非支配解集中均匀选择的3个解，只列出前5个叶素.叶片气动性能需要最小的启动时间和最大的功率系数，两者不可兼顾.因此需要根据经验或工程人员的偏好选择其中的某一个解作为最优解.

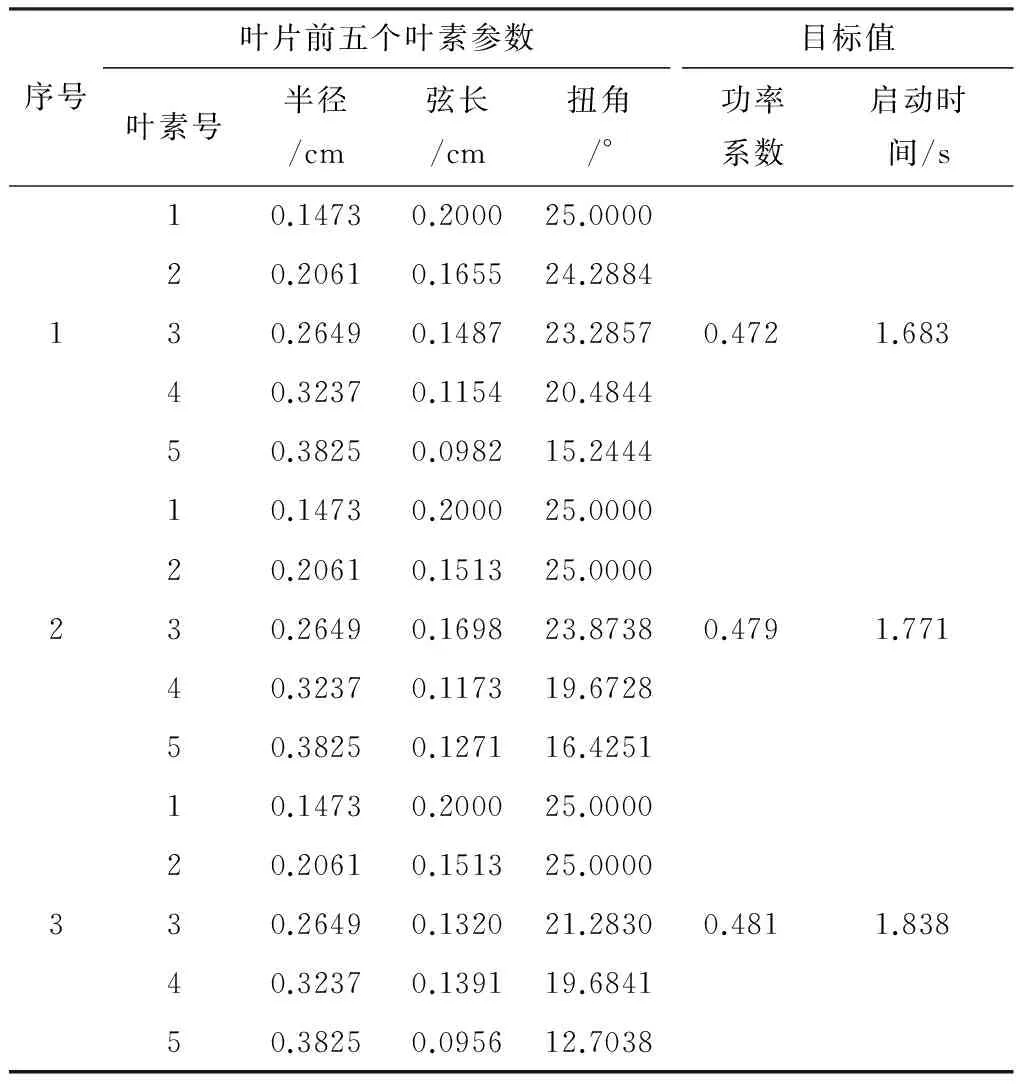
表1　小型水平轴风力机叶片多目标优化的部分非支配解

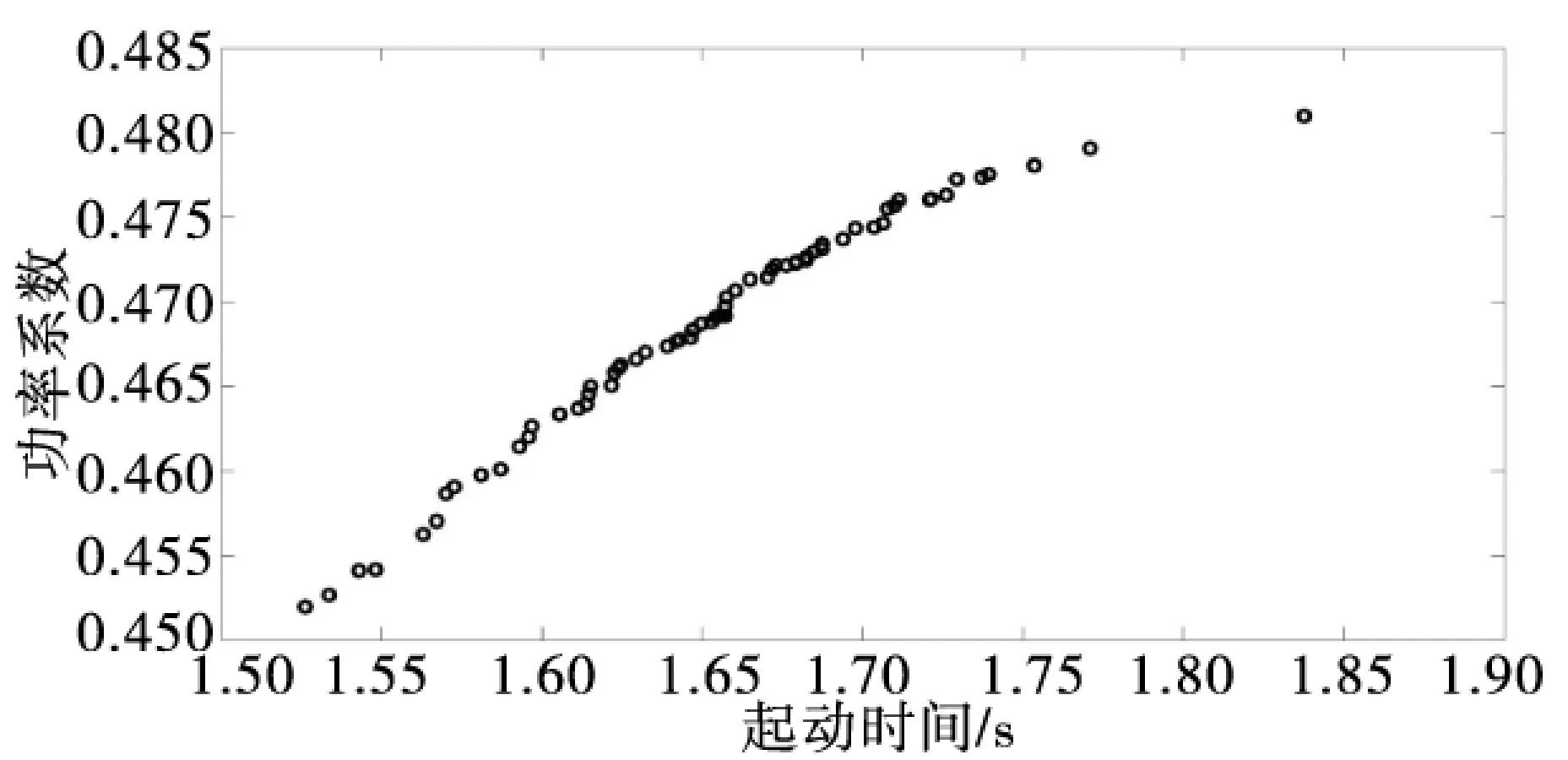
图4　多目标优化结果

4　结论

风力发电是目前最具规模化开发条件和商业化发展前景的可再生能源发电方式.风轮将风的动能转换为机械能，是风力机的核心部件.叶片决定了风能的转换效率，是风轮的关键部件.小型风力机不仅要求有良好的气动性能还要求启动时间短.为了优化叶片形状，本文先分析叶片翼型对气动性能的影响，选择叶片翼型.然后以微型遗传算法优化叶素的弦长、半径和扭转角获得良好的功率系数和较短的启动时间.为叶片的气动性能优化提供一种思路.

[1] 赵振宙,王同光,黄娟,等. 安装角对立轴风轮气动性能影响分析[J] .中国电机工程学报,2014,34(8): 1304-1309.

[2] 吕黎,毕长飞,崔鹏宇. 垂直轴风力机叶片翼型的气动性能分析[J]. 热力发电,2014,43(12): 126-129.

[3] 孙凯,温彩凤,汪建文. 小型风力机的两种翼型应力特性对比[J]. 内蒙古科技与经济,2014,321(23):89-90.

[4] 曲建俊,许明伟,梅毅,李岩,等. 叶片数对VAWT- SWS低风速自起动性能的影响[J].农业机械学报, 2014,45(5):173-178.

[5] 朱杰,蔡新,潘盼.风力机叶片结构参数敏感性分析及优化设计[J].河海大学学报(自然科学版),2015, 43(2):156-162.

[6] 林锁鑫,薛扬诗,郭良祥.小功率(小型)风力发电机叶片优化设计方法[J].中国高新技术企业,2015，338(23)：37-38.

[7] Liu, G.P. Han, X. Jiang, C. An Efficient Multi-objective Optimization Approach Based on the Micro Genetic Algorithm and its Application [J]. International Journal of Mechanics and Materials in Design, 2012, 8(1):37-49.

[8] Xin Liua, Zhiyong Zhang. Optimization of Astronaut Landing Position Based on Micro Multi-objective Genetic Algorithms [J]. Aerospace Science and Technology, 2013, 29(1): 321-329.

[9] 陈云程，陈孝耀，朱成名.风力机设计与应用.上海:上海科学技术出版社,1990(5):20-35.

[10] Tony Burton, David Sharpe, Nick Jenkins, e ta. Wind Energy Handbook [M]. John Wiley &Sons Ltd, 2001: 78-378.

Aerodynamic Performance Analysis and Optimization for a Small Horizontal-axis Wind Turbine Blade

LI Jian-hua1,2,WEI Ke-xiang1，WANG Gao-sheng

(1. College of Mechanical Engineering, Hunan Institute of Engineering, Xiangtan 411101, China;2. Hunan Province Cooperative Innovation Center for Wind Power Equipment and Energy Conversion,Hunan Institute of Engineering, Xiangtan 411101, China)

The wind wheel blades' aerodynamic performance determines the power and load characteristics of wind turbine，while the blade airfoil is the key factor of influencing the blade aerodynamic performance. Different types of airfoil shape have certain aerodynamic rules. To enhance the wind turbine performances and shorten start-up period, a small horizontal-axis wind turbine blade is carried out to study the aerodynamic performance by comparing with the different blade airfoils. The optimization model is built with a micro multi-objective genetic algorithm, in which the parameters of blade element (such as chord length, radius and twist) are optimization variables, and the maximum power coefficient and the minimum start-up period are optimization objectives. The effectiveness of the method is verified.

small horizontal-axis wind turbine; aerodynamic performance; blade airfoil; a micro multi-objective genetic algorithm

2016-01-16

国家自然科学基金资助项目(11472103)；湖南省教育厅科研资助项目(15B057).

李建华(1976—),男，硕士，讲师，研究方向：机械设计及理论.

TK83

A

1671-119X(2016)03-0024-04