非高斯高度分布函数构造的表面形貌的表征

李炯，林炜轩，程鹤登，陈榕杰，王江涌

（汕头大学 理学院，广东 汕头 515063）

表面粗糙度是评定各机械零件表面加工质量的一个重要指标。表面粗糙度理论及标准在过去的几十年里得到了巨大的发展，出现了接触式（比较法、印模发和触针法）和非接触式（光切法、实时全息法、散斑法、光外差干涉法和AFM测量法）的粗糙度测量方法[1—2]。而随着微机处理技术、集成电路技术等的发展，出现了图像法、分形法、Motif 法、功能参数集法等各种评定方法[3—6]。由于对表面形貌描述的精度需求不断增加，导致了描述表面粗糙度的参数也在不断增加。我国 GB/T 3505—2009推荐了18个二维粗糙度参数专业术语用，以描述二维表面形貌特征[7]。而多达41个粗糙度参数却又给实际应用带来了不便[8]。

高度分布函数是评估表面形貌的一个非常重要的指标，虽然它直观地给出了表面形貌高度的分布情形，但它与表面形貌并非有着一一对应的关系。同一高度分布函数可以产生各种各样的表面形貌，而不同的高度分布函数又可以用同样的方式构造出有关联的表面形貌。一般情况下，表面形貌的高度分布函数满足高斯型分布函数分布，但并非所有的表面形貌都满足高斯型分布[9—10]。本文用同一高度分布函数(包括高斯和非高斯型)构造不同的表面形貌，同时，用不同高度分布函数以同样的方式构造出表面形貌，再研究表征这些表面形貌各参数之间的关系。特别讨论了非高斯型高度分布函数对表征表面形貌高度类粗糙度参数的影响，并在此基础上提出了可以简化表征参数数目的方案。

1 表征参数与高度分布函数

1.1 表面形貌的表征参数

现今评估和衡量表面形貌粗糙度的参数多达 41个，其大致可以分为：高度类参数(Amplitude parameters)、间距类参数(Spacing parameters)和混合类参数(Hybrid parameters)。不同类型的参数描述的对象有所差异，高度类参数对应于表面形貌的纵向特性评定，间距类参数对应于表面形貌的横向特性评定，混合类参数是高度信息和间距信息的结合，任意高度或间距的变化都会导致混合类参数的改变[8]。其中，高度类参数作为比较重要的参数，多应用于对表面形貌的描述[6,12]。因此，本文选取高度类的 16个参数来表征所构造的表面形貌的相关特征，见表1。

表1 高度类参数列表Tab.1 List of the amplitude parameters

1.2 高度分布函数

高度分布函数（Height Distribution Function，HDF）是对表面形貌的高度分布进行统计的直方图。因为表面形貌是由很多不同高度的点组成，可以将表面形貌看作一个数组。统计表面形貌在[y,y+δy]高度范围内的点数，当δy的值趋于零时，就能够得到高度为y所对应的点数n。将y作为横轴，n作为纵轴，就可以得到该表面形貌所对应的高度分布函数（HDF）。如图1所示，左边为表面形貌的剖面图（profile），右边即为表征该剖面的高度分布函数。图2给出了本文将要讨论的6种不同的高度分布函数。高度分布函数不仅包含了表面形貌的高度信息，而且还可以通过其构造各种新的表面形貌。

2 同一高度分布函数构造的表面形貌特征

2.1 余弦型高度分布函数构建的表面形貌

给定一个余弦型的高度分布函数：h代表高度，p代表点数，-π/2≤h≤π/2（如图 2b所示）。当ℎ取一定的抽样间隔时（如h=0.0001时），则高度h和对应的点数p都被分为一系列不连续的数值，那么就可以将h和p视作数组。表面形貌对应的数组y大小为∑p，然后采用随机（或某一特定）的取点排列形式，将点数p随机赋值到数组y中，就构造出一个表面形貌。

通过计算机模拟，可以得到一系列随机排列、数组的大小均为∑p的表面形貌，具体的构建方法如下：

1）对数据进行预处理，利用计算机的随机函数，选取表面形貌的随机起点h0，则其对应的点数为p(h0)。

2）判断原始数组p是否为零，如是，结束程序。

3）通过随机函数，确定从原始数组取高度点的方向（左/右）、取点范围Δh和取点间距n。

4）判断高度对应的点数p(ℎ)是否为为零，如不是，保存ℎ，点数p(ℎ)自减 1，跳到下一个高度ℎ+n。

5）判断高度ℎ+n是否大于Δh，如是，返回第2步；否则，执行第4步。

通过上述随机取点、放置的方式，本文构建了一系列不同的随机数组，即一系列不同的、服从同一个余弦型高度分布函数的表面形貌。

2.2 参数统计

通过模拟，可以得到一系列随机排列、数组大小均为∑p的表面形貌。本部分共进行多次模拟，并选取其中10组数组（表面形貌）作为实验对象。分别对所构造的表面形貌的高度类粗糙度参数进行统计，结果如下。

2.2.1 与高度位置无关的参数

在高度类粗糙度参数中，Ra、Rq、Rsk和Rku与高度位置信息无关，因此，对所构造的10个表面形貌来说，这4个参数保持一致，其大小Ra=0.577 μm，Rq=0.691 μm，Rsk=−1.30×10−5，Rku=2.194。

由于Ra与Rq反映的都是轮廓高度的变化情况，只要整体的表面形貌高度信息保持不变（即同一个高度分布函数），则Ra和Rq的数值都会保持一致，无论表面形貌的高度是按何种方式来随机排列。

表面形貌的偏度Rsk通常是用来衡量表面形貌关于中线的对称性。对于对称的高度分布函数，表面形貌的偏度为零。这个参数可以分辨具有相同Ra、Rq参数的不同表面形貌。因为高度分布函数包含了除位置外所有的高度信息，所以，这10个表面形貌的数组元素都取自同一高度分布函数，其数组元素一样，只是分配的位置不同。因此，Rsk参数具有相同的值。

表面形貌的峰度Rku通常是用来描述表面形貌的陡峭程度。如果Rku＜3，则表面形貌处于平峰态，只有少量尖锐的波峰和波谷；如果Rku＞3，则说明表面形貌处于尖峰态，具有较多尖锐的波峰和波谷。与Rsk参数相似，由于10个表面形貌的数组元素一样，只是位置不同，所以表面形貌所包含的尖锐波峰和尖锐波谷数量应该具有一致性，Rku的数值也相同。

2.2.2 由波峰、波谷决定的高度参数

由波峰、波谷决定的参数分别为：Rp（最大峰值）、Rv（最大谷值）、Rpm（轮廓峰平均高度）、Rvm（轮廓谷平均深度）、Rmax（轮廓最大的高度）和k（轮廓度因子）。其中，Rp、Rv、Rmax和k的数值分别具有相同的数值，与表面形貌的高度位置无关，且Rp=1.507 μm，Rv=1.508 μm，Rmax=3.141 μm，k=0.500；Rpm和Rvm的数值随着表面形貌的不同而不同，如图3所示（图中的横坐标1至10表示表面形貌的编号，以下类同）。

由于给定的高度分布函数满足-π/2≤h≤π/2，即高度的最小值、最大值分别是-π/2和π/2，因此构建出的表面形貌最大谷值Rv和最大峰值Rp分别为-π/2和 π/2。此外，因为另一高度粗糙度参数Rmax=Rp+Rv，根据以上的论述，Rmax的数值必定为π。而k=Rv/Rmax，由于Rv和Rmax的数值均保持不变，所以，k的数值也保持一定。

由于Rpm和Rvm计算的是5个抽样长度内的最大峰值的平均值与最大谷值的平均值。若5个最大的峰谷值不是均匀地分配在5个抽样长度内，则就会导致Rpm和Rvm参数数值的差异，因此，这两个参数的大小受到峰谷位置的影响。

2.2.3 与表面形貌高度位置相关的参数

高度类粗糙度参数是统计表面形貌的纵向分布特征，但由于实验的表面形貌是将高度信息随机分配在数组上，这便导致部分高度类参数在进行统计时，会随着表面形貌的横向分布而呈现出不同的数值。在统计的参数中，Rz（微观不平度十点平均高度）、Rti（局部最大峰谷高度）、Rtm（最大峰谷高度均值）、Ry（最大峰谷高度）、R3y（第三点高度）和R3z（第三点高度均值）便是随高度位置信息变化而变化的粗糙度参数。以上各个参数随表面形貌不同的变化情况如图4所示。

由图4中所显示的参数数值的变化情况可以得出：参数Rz、Rti、Rtm、Ry、R3y、R3z（Rti和R3y没有列出）是不断变化的。由于10个构造的表面形貌是通过对高度分布函数的高度信息进行随机排列而得到的新数组，对于每一个表面形貌，其波峰出现在一个位置的概率是不定的。而这部分所涉及的 6个高度类粗糙度参数都是随高度位置而变化，因此这 6个粗糙度参数会随着实际表面形貌的峰谷排列情况而改变，从而体现在表征表面形貌随高度位置变化的参数数值的波动，如图4所示。

3 不同高度分布函数构造的表面形貌特征

3.1 6种不同的高度分布函数

给定6种不同形状的高度分布函数(见图2），采用同一种方式来构建表面形貌。其中，h代表高度，p代表点数，-π/2≤h≤π/2。每个高度分布函数都以对照组的高斯型高度分布函数为标准，进行归一化。此部分的表面形貌构建方式同样采用随机的取点排列形式，将高度分布函数的点数p随机赋值到数组y中，最后得到一个表面形貌。

对照组：高斯型高度分布函数。实验组：A对称型非高斯高度分布函数，对称型高度分布函数选用余弦型、等腰三角形和等腰梯形高度分布函数；B非对称型非高斯高度分布函数，非对称型高度分布函数选用三角形和直角三角形高度分布函数。

此部分的表面形貌构建方式与之前的有所差异，其具体的构建方法如下：

1）对数据进行预处理，然后将从分布函数得到的高度排列∑p打乱，并定义表面形貌的最大高度差Δh。

2）利用程序的随机函数，确定表面形貌y的起点y(1)并将其从∑p中剔除。

3）从高度排列∑p中提取高度点p，与y(1)进行比较。如果满足两者之差在△ℎ内，则将其归入到表面形貌y中，并将其作为起点（同时从∑p中剔除）；否则，把p与表面形貌的终点y(end)进行比较，判断是否满足两者差在Δh内，如果满足，则将其归入到表面形貌y中，并将其作为终点（同时从∑p中剔除）。

4）检测原始高度排列∑p是否为零，若是，则结束构建；否则，返回第3步继续构建。

通过上述的程序过程，本文利用图2给出的6种高度分布函数，用以上同一种方式构建了一系列的随机表面形貌，然后对粗糙度参数进行统计分析。

3.2 参数统计

每种高度分布函数选取10个表面形貌作为实验对象，总共获得60个表面形貌的数组元素，并对这些模拟表面进行参数统计。所选用的参数是上述16个高度类粗糙度参数，其统计结果如下。

3.2.1 由高度分布函数确定的参数

在高度类参数的统计时，发现有4个参数只跟随高度分布函数的变化而变化，它们与表面形貌高度位置的横向分布无关。这 4个参数分别是Ra、Rq、Rsk、Rku，它们的数值变化随高度分布函数的变化情况如图5所示（图中用i-trapezoid、i-triangle、ra-triangle分别表示等腰梯形，等腰三角形和直角三角形HDF，以下类同）。

在第2节已说明，对应于同一个高度分布函数，Ra、Rq、Rsk、Rku保持数值不变。而图 5表示，随着高度分布函数对称性的逐渐消失，Ra、Rq呈现出正相关的情形，当对称性达到最小时（即直角三角形时），Ra、Rq值达到极大值，即随着对称性的消失，其数值有一定的增加趋势。

而Rsk、Rku的变化趋势虽不像负相关的情形，但也可明显看出，当对称性消失时，Rsk和Rku的数值明显小于对称性时的数值。分布函数处于对称的情况时，参数数值明显区别于非对称性时的参数数值。

3.2.2 由峰值、谷值限定的参数

在统计过程中，有4个参数始终保持不变，它们不随高度分布函数的改变而变化，也不随表面形貌的高度位置信息的变化而变化。这4个参数分别是Rp、Rv、Rmax和k。另外，参数Rz的数值虽然随着高度分布函数形状改变而变化，但其数值变化较小，因此将其归入这部分中讨论。它们的数值大小如表2所示。

由于在用计算机模拟表面形貌时，给定的6个高度分布函数的高度都在-π/2≤h≤π/2之间，类似于之前说明的情况，最大峰值、谷值的数值只能被限制在-π/2和π/2。因此，轮廓最大高度只会等于π，k只会等于1/2，不会随高度位置信息的变化而发生改变。

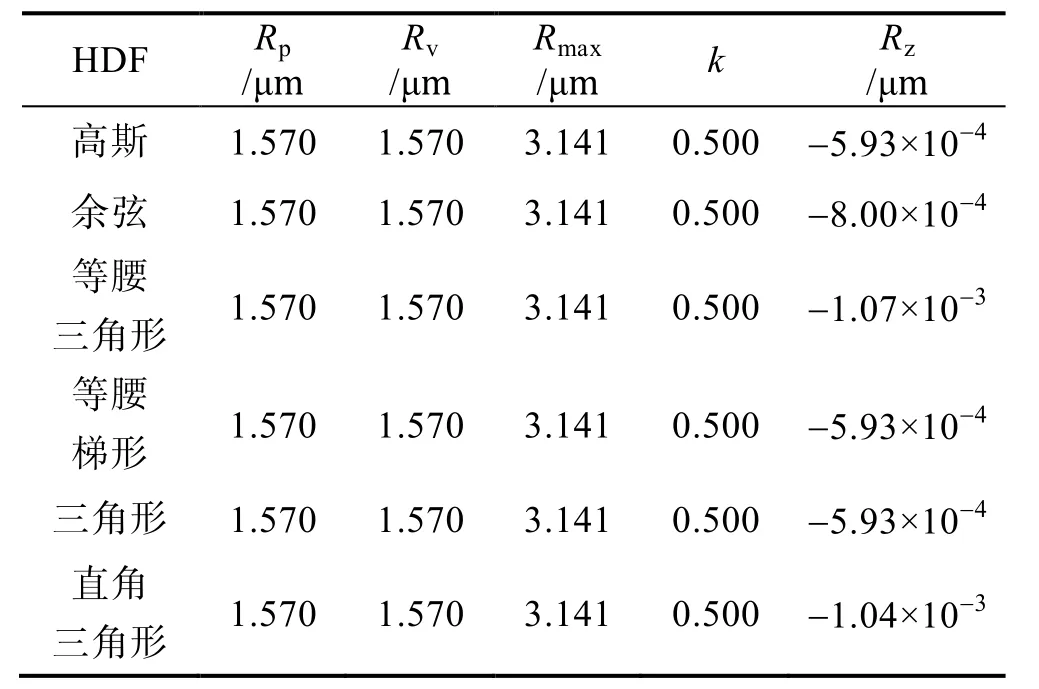
表2 Rp、Rv、Rmax、Rz和 k的数值Tab.2 Values of Rp, Rv, Rmax, Rz and k

另外，Rz是表示最高峰值与最深谷值之间的差值平均值。由于计算机程序模拟表面形貌时，是将最深谷值设置为略微大于最高峰值的，因此Rz的数值是负值。此外，Rz数值的变化是因为在构建表面形貌时，会存在某些高度点因不符合取点原则而被舍弃的情况，当分布函数内最大的（或最小的）几个高度点被舍弃时，便会造成Rz数值的波动。

3.2.3 随高度分布函数变化的参数

除了以上9个参数，剩下7个参数（Rpm、Rvm、Ry、Rti、Rtm、R3y和R3z）都会随着表面形貌的高度位置随机改变而发生变化。对于同一种高度分布函数，这些高度类参数的数值都不是恒定的，而对于不同的高度分布函数，它们的数值也不相同，而且没有显示出一定随对称性改变的规律，更多地是显示出数值的波动。由于Rtm和Ry表示的是参数Rti的平均值和最大值，因此这三个参数的图像变化情况是一致的。而R3z和R3y分别表示表面抽样长度内的第三点高度和第三点高度的最大值，其表征的内容与Rti、Ry相似，因此这两个参数的变化与Rtm、Ry和Rti极其相似。因此，可选用Ry来反映这四个参数的变化情况。这部分参数的数值变化见图6。

由图6的数据可以看出，这些参数随着高度分布函数的不同而无规律波动，这种数据的波动是表面形貌的高度位置随机分配和高度分布函数的差异所致。

4 结论

本文分别利用同一非高斯型高度分布函数和不同的非高斯型高度分布函数来构建表面形貌，并分析其高度类粗糙度参数。根据统计结果得出的结论如下。

1）由同一种高度分布函数构建的表面

当高度类参数满足对整个表面形貌的数学统计，忽略高度数据的位置情况或是与整个表面形貌的一些极值有关，这些极值不会随着位置的变化而影响到本来的特性（如表面形貌的最高峰和最低谷）时，参数数值保持不变。

当高度类参数只是满足对局部表面形貌的数学统计，统计位置的不同会造成参数的变化或与表面形貌的极值无关时，参数数值会表现出不确定性。

2）由不同种高度分布函数构建的表面

从区分表面形貌的角度出发，可以根据要求减少参数的测量：若只需要分辨表面形貌时，可只测量Ra、Rq、Rsk、Rku。由于它们只和高度分布函数有关，且这4个参数会随着高度分布函数对称性的改变而发生变化，因此可通过测量这4个参数来简要区分不同对称性高度分布函数构造的表面形貌。

当测量出表面形貌的峰谷最大值时，可以根据其测量值来确定另外4个参数Rp、Rv、Rmax、k的数值，从而进一步对表面形貌进行区分。而如果需要对一个表面形貌的细节进行细致分析时，可计算剩余的8个参数来分析其详细的高度位置信息。

3）应用

现应用上述结论，对图1中三种不同的表面形貌进行表征区分。首先利用分布函数的形状差异，可对比高斯型（或余弦型）表面形貌（图1a或b）和三角形表面形貌（图1c）。高斯型（余弦型）分布函数是对称型的结构，对应的表面形貌的高度点均匀地分配在中线两侧，并且在中线位置的高度点最为集中。而非对称结构的三角型分布函数，其表面形貌的高度点更多地集中于中线下方。对于满足分布函数形状差异较大的表面形貌，可以通过对比其纵向分布特征，即高度点的集中范围来简单表征形貌之间的差异，如通过对比图1a与c的纵向分布差异来区分表面形貌。这是高度分布函数的一个直接应用。

但在表征高斯型与余弦型这两种表面时，由于它们的纵向特征较相似，无法简单判断，则必须利用粗糙度参数来表征其差异、区分。根据上述的选取建议，对比高斯型和余弦型表面时，可选用参数Ra（Ra-gau=0.6403、Ra-cos=0.7664）和Rku（Rku-gau=2.1524、Rku-cos=2.1940）来反映两种表面剖面的细微差异，进行初步简单区分。假如需要对形貌的特征进行较高精度的表征时，也可适当地选用其他参数（如Rpm、Rvm、Rti等）来分析表面形貌的横向特征，进而更精确地反映形貌的信息。