高精度自适应小波神经网络人工智能方法探索*
2016-08-31刘经纬普1首都经济贸易大学信息学院北京100070北京工业大学电子信息与控制工程学院北京10014清华大学信息技术研究院北京100084
刘经纬,赵 辉,周 瑞,王 普1.首都经济贸易大学 信息学院,北京 100070.北京工业大学 电子信息与控制工程学院,北京 10014.清华大学 信息技术研究院,北京 100084
高精度自适应小波神经网络人工智能方法探索*
刘经纬1,2+,赵辉3,周瑞2,王普2
1.首都经济贸易大学 信息学院,北京 100070
2.北京工业大学 电子信息与控制工程学院,北京 100124
3.清华大学 信息技术研究院,北京 100084
LIU Jingwei,ZHAO Hui,ZHOU Rui,et al.Exploration of high-precision adaptive wavelet neural network artificial intelligence method.Journal of Frontiers of Computer Science and Technology,2016,10(8):1122-1132.
摘要:针对当前人工智能方法存在的训练精度瓶颈问题和智能系统对高精度人工智能方法的迫切需求问题,结合小波分析和BP(back propagation)、RBF(radial basis function)神经网络的优点,提出了自适应小波神经网络(adaptive wavelet neural network,AWNN)方法,将其应用于智能视频分析系统和智能控制系统,并验证了AWNN方法可以取得更好的收敛性、准确性、精度等。通过对AWNN方法与经典的神经网络进行理论分析,并与计算机仿真进行对比分析,验证了该方法可以提升经典神经网络的速度和精度;进而通过将AWNN方法植入真实的视频分析系统进行实验,验证了AWNN方法与现有的视频分析技术相比具有更准确的内容分类能力;最终将AWNN方法与经典控制方法相结合,通过与两种现有的神经网络控制方法进行对比分析,验证了AWNN控制方法具有更好的控制性能。
关键词:小波神经网络;智能系统;视频分析;智能控制系统;神经网络控制
1 引言
经典的人工智能方法主要可以分为两大类:一是基于规则和推理技术的人工智能,例如专家系统、模糊逻辑、搜索方法、遗传算法、群集智能和基于规则的机器学习方法;二是基于人脑原理的神经网络技术,例如前馈神经网络、反馈神经网络、复合神经网络和基于神经网络的机器学习方法。
上述经典的人工智能方法在知识的海量存储和智能单元的处理能力(智能算法的局限性)两个方面遇到了瓶颈,导致其智能在一些简单的领域被有限地应用。经典的人工智能方法在学习知识的容量、精度和稳定性三方面亟待提升。
2012年以来,微软、苹果、谷歌、百度等公司相继在人工智能领域进行了重量级战略投资,开发了Cortana、Siri等人工智能系统,并发表了大量研究成果。2015—2016年,谷歌公司研究人员在“Nature”杂志发表多篇论文[1-2],展示了将深度人工智能方法应用于计算机,从而实现对49项游戏的学习和操控。计算机通过实时在线学习,对半数以上比赛的操控效果达到了与测试人员非常接近的水平,在部分比赛中超过测试人员。研究表示“该成果是世界上第一个能面对不同任务进行学习,对不同系统进行控制并胜出的人工智能算法。”计算机科学和IT领域开始向人工智能应用领域深水区迈出步伐,对具有高性能的人工智能理论和应用进行研究成为计算机科学探索的前沿阵地。2016年3月,谷歌公司采用上述理论研发的AlphaGo人工智能系统在围棋项目人机对战中,战胜了世界围棋冠军李世石。
神经网络模型本质上更接近于人脑智能的产生原理,通过对上述人工智能领域最新的研究成果和趋势进行分析,基于神经网络的人工智能方法具有更加广阔的研究前景。其中,对神经网络的结构和神经元节点的特性进行改进,成为人工智能领域再一次跨越式发展的突破口。本研究针对后者进行探索,即探索改进神经元节点。研究成果可以进一步应用于前者,即在调整神经网络接口的基础上实施对神经元节点的改进,从学习知识的容量、精度和稳定性三方面对经典人工智能模型进行改进。
经典的神经网络可以分为前向网络和反馈网络。其中应用最广泛的两种神经网络模型是BP (back propagation)神经网络和RBF(radial basis function)神经网络,还有很多基于这两类模型的改进模型。传统的BP网络算法[3]采用基于误差反向传播的梯度算法[4],充分利用了多层前向网络的结构优势,算法相对成熟,具有很多应用案例;RBF网络[5]利用差值法的研究成果,采用前馈的结构,各有优缺点。
BP神经网络模型的优点是:(1)具有较强的非线性映射能力;(2)具有高度自学习和自适应的能力;(3)具有良好的泛化能力,即对新鲜样本的适应能力;(4)具有一定的容错能力。
BP神经网络存在的缺点和问题是:(1)局部极小化影响精度;(2)算法收敛速度慢;(3)对训练样本依赖。
RBF神经网络[6]采用了与BP神经网络不同的局部激励函数,很大程度上克服了BP神经网络的上述缺点。RBF神经网络的优点是:(1)具有唯一最佳逼近的特性,无局部极小问题;(2)具有较强的输入和输出映射功能,在前向网络中RBF网络是完成映射功能的最优网络;(3)学习过程收敛速度快。
RBF神经网络存在的问题是:(1)RBF隐含层节点的中心难以获得;(2)隐含层节点数难以确认;(3)训练过程非常不平稳,频繁出现系统误差跳变。
小波分析被称为数学显微镜,小波变换可以通过尺度伸缩和平移对信号进行多尺度分析,能有效提取信号的局部信息[7],具有良好的函数逼近能力和模式分类能力[8]。小波神经网络已被证明在逼近单变量函数时是渐近最优的逼近器[9]。
本文希望同时解决上述3个问题:BP神经网络陷入局部极小问题,RBF神经网络训练过程不稳定问题,以及在神经元规模有限的情况下训练精度瓶颈问题。试图探索将上述3种算法优点相结合,从而克服彼此的缺陷,并引入对样本的自适应机制,构建出自适应小波神经网络[10](adaptive wavelet neural network,AWNN)方法。
本文首先验证了AWNN方法相对于经典神经网络的性能提升;进而应用于智能视频分析系统,在真实环境中验证了AWNN方法应用相对于其他经典神经网络应用的性能提升;最后与经典控制方法相结合,通过计算机仿真的方法验证了AWNN控制系统相对于其他经典神经网络控制系统的性能提升。
新型网络具有上述3种算法的优点[11]以及如下有益效果:(1)隐含层节点采用尺度变换函数,克服了局部极小点问题;(2)降低了隐含层神经元相关性,较之RBF神经网络,收敛过程更加平稳,收敛速度得到提升;(3)具有更好的局部特性和多分辨率学习能力,提升了神经网络的训练精度,特别是在神经元节点规模有限的情况下,提升了神经网络的学习能力;(4)自适应层和综合层的设计使该算法在应用中具有自适应样本能力;(5)为深度神经网络学习方法中隐含层节点的改进、算法的分辨率和精度提升提供理论和实验依据。
2 AWNN模型建立
2.1AWNN设计
AWNN设计原理如下:(1)BP神经网络结构中通过反向误差传播原理,可以获得稳定、快速、单调的误差收敛效果;(2)RBF神经网络中隐含层神经元采用基函数变换算法,相当于增加了误差调整维度,从而可以跳出陷入局部极小的情况;(3)小波变换算法的尺度变换算法具有极好的局部信息提取能力。
AWNN设计思路如下:采用BP神经网络拓扑结构和RBF神经网络隐含层神经元结构,将小波尺度变换函数作为神经网络隐含层的活化函数[12],并设计对样本的自适应机制。
自适应小波神经网络的结构由5层组成:输入层、自适应层、小波函数计算层、输出层、综合层,如图1所示。
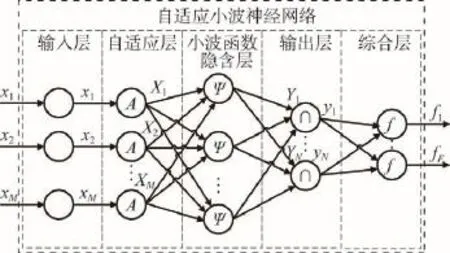
Fig.1 Structure of adaptive wavelet neural network图1 自适应小波神经网络结构图
框架理论[13]的结论是:框架边界越接近,稳定性就越好,但也会造成数据冗余。选取满足框架条件的Morlet小波函数,如式(1)所示:

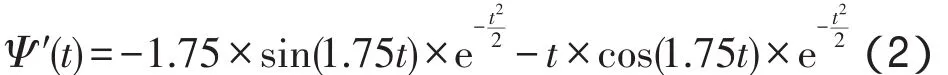

对式(1)求一阶导数,如式(2)所示:
其中,Ψj为第 j个小波基,j=1,2,…,n,n为小波基的个数;aj为第 j个小波基的伸缩因子;bj为第 j个小波基的平移因子。
输出层第i个变量Y(i)的计算如式(4)所示:
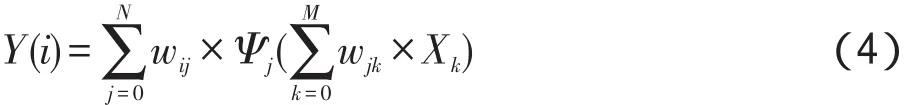
其中,Xk为隐含层输入;wij和wik为连接权值。
按照式(5)定义熵函数E:
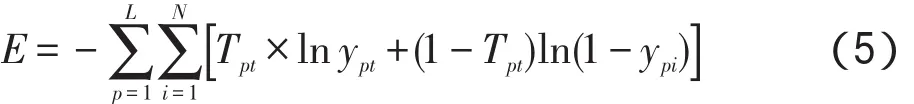
对式(5)求偏导数,如式(6)至式(9)所示:
唉,杨小水叹了一声。还是应了那句老话,不是没报时候未到啊。《狸猫换太子》那戏,刘皇后最后落了什么好?自己的儿子没有成年就病死了,皇帝将贤王的儿子收为养子,后来又立为太子。知道这个孩子是谁吧?
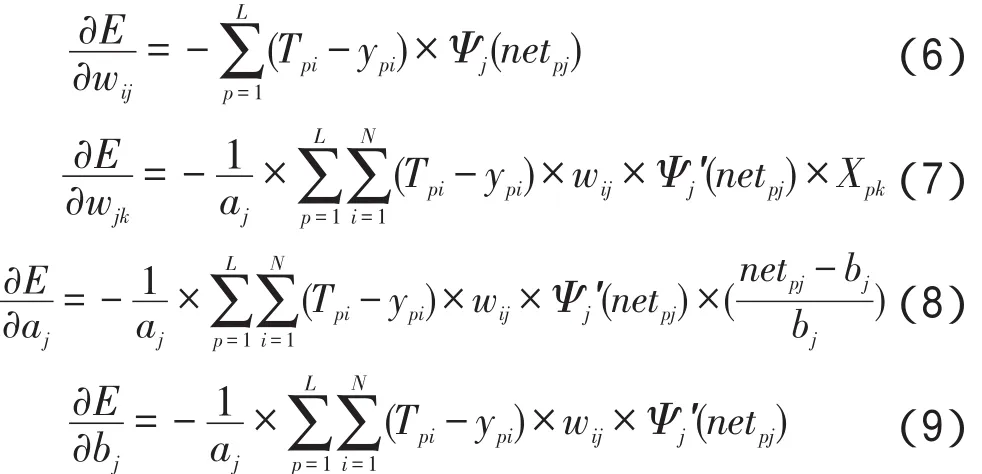
依据梯度下降法,得到AWNN权值调整公式,如式(10)至式(13)所示:
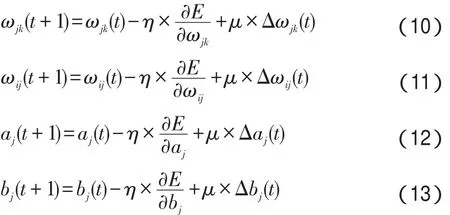
其中,η为网络学习速率;μ为动量系数。
2.2AWNN算法特性理论分析
2.2.1收敛性分析
设神经网络训练样本集为{Xk(t),dk},其中Xk(t)∈ (C[0,T])n,dk∈R,则给定训练误差的情况下,由式(4)、式(5)定义的小波神经网络应满足方程组如式(14)所示:

其中,dk为期望输出。对式(14)求解,若系数矩阵正定,则有唯一解。采用迪汉洛夫正则化理论,寻求F(X)使得式(15)泛函最小,即可求解[14]。
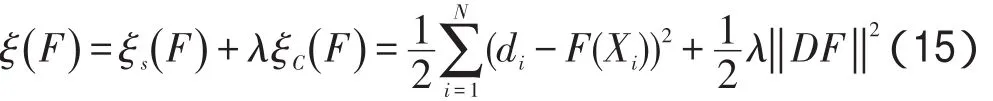
如果AWNN满足框架条件,则可以证明AWNN可以任意精度逼近训练样本[15],即满足式(16)。
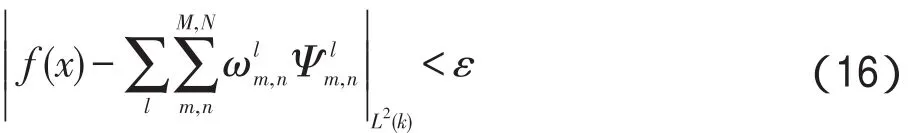
2.2.2效率分析
由式(10)至式(13)可以看出,小波基尺度变换函数增加了两个尺度变化参数aj和bj,也可以看作两组权值,从而打破了BP神经网络中仅有ωij和ωjk两组权值在最速下降法训练过程中的单调变化特性。在一次训练中,4组权值的共同训练提升了误差变化率,使得AWNN训练次数降低。但是,Morlet小波函数及其导数中存在很多零点,这些零点在训练过程中将会导致Δaj、Δbj、Δωij和Δωjk出现归零的情况,这将是导致训练效率降低的隐患[16]。同时,Morlet函数与Sigmoid函数相比,其波动性更大,对于一个较小的权值调整量Δωij<ε,经过式(4)的计算,会被快速放大。因此AWNN算法中初值对算法效率影响极大。
构建神经网络效率评估模型,如式(17)所示:
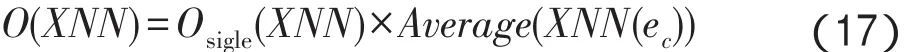
其中,O(XNN)表示X神经网络算法的时间复杂度;Osigle(XNN)表示X神经网络算法单次训练算法复杂度,例如Osigle(AWNN)可以表示为:Average(XNN(ec))表示在各种神经网络达到相同训练误差时的平均训练次数,该数值可通过对仿真结果进行统计的方法获得。
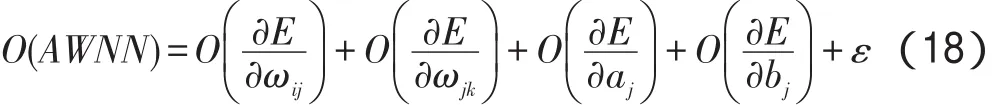
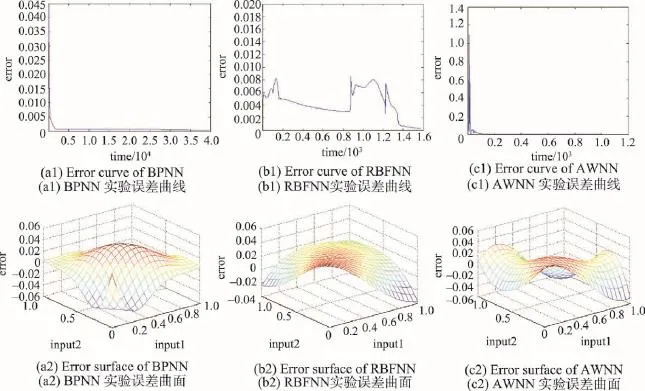
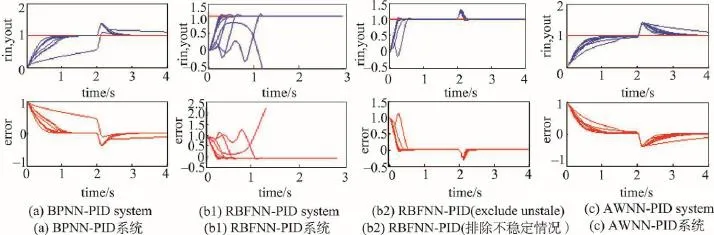
当神经网络权值与尺度变换参数初始化算法为随机数且满足0至1区间均匀分布,不同神经网络的学习效率与惯性系数相同,目标误差一致,样本数据一致时,O(XNN)即可表征各算法时间复杂度。常见算法的时间复杂度:O(1) 2.3AWNN验证研究 本节的实验目标是:通过计算机编程实现3种神经网络BPNN、RBFNN、AWNN。首先验证算法的可行性和基本特征,进而验证可达性,即AWNN能否提升神经网络的最大训练精度。 训练集设计为二维平面上的每个点到三维曲面上每个点的映射关系,即输出曲面上的每个点的高度值z与输入平面上每个点坐标(x,y)之间的映射关系,如式(19)所示: 在输入平面上取3×3个点构成训练集的输入集X,计算得到训练集的目标输出集T: 在输入平面上取21×21=441个点,每个点的坐标构成测试集Xt每一个输入,因此Xt为2行441列的矩阵,每一列为一个坐标,测试集的输出Tt为1行411列的矩阵,计算方法同样如式(19)所示。 2.3.1AWNN可行性与特征实验 对BPNN、RBFNN和AWNN设计相同的实验参数,构成对比实验:(1)令算法终止的条件为训练次数到达上限max_epoch=100 000,或每个训练样本的前向计算值与目标输出值的误差全部都小于目标误差err_goal=0.1;(2)设置一组实验总轮数均为case_repeat=10;(3)设置相同的学习效率参数lr=0.2,相同的惯性系数la=0.3。计算机仿真结果如图2所示。 Fig.2 Simulation results of feasibility verification图2BPNN、RBFNN和AWNN仿真实验结果 从图2中可以看出:3种算法均可以完成训练。BPNN训练过程中误差单调递减,即可能陷入局部极小;RBFNN训练过程中递减的过程经常会被打破,而且跳变的过程频率和幅度都比较大,这种特性有利于概率性地获取高精度,也带来了应用过程中不稳定的可能性;AWNN算法误差跳变的过程出现在训练前期,误差减小的过程很快进入了平稳的状态。因此可以认为AWNN克服了BPNN陷入局部极小的问题,继承了BPNN训练过程平稳和快速的优点,同时也克服了RBFNN频繁出现跳变产生的不稳定问题,但保留了RBFNN跳出局部极小点的能力。RBFNN测试集输出曲面最平滑,BPNN测试集输出曲面效果最差,AWNN介于其间。 进一步分别对3种算法连续仿真10次,得到实验结果如表1所示。表1进一步表明:(1)3种算法均存在训练完成(收敛)的情况。(2)AWNN平均训练次数最少,即训练效率最高,约为BPNN的1/4,RBFNN 的1/8;RBFNN平均训练次数最多,即训练效率最低。(3)BPNN训练误差曲线是单调递减的,存在局部极小点问题,导致大多数训练无法达到高精度;而RBFNN和AWNN则可以跳出局部极小点,存在达到更高精度的概率。 Table 1 Feasibility experiment results of BPNN,RBFNN andAWNN表1BPNN、RBFNN和AWNN可行性实验结果 2.3.2AWNN高精度实验 保持3种神经网络训练参数一致,将目标精度逐渐提高(目标误差err_goal=0.1逐步减小)并多次重复训练,对比3种方法的训练过程和结果。即设定目标误差err_goal=0.05,分别连续仿真case_repeat=10次,实验结果如表2所示。 Table 2 Reachability experiment results of BPNN,RBFNN andAWNN表2BPNN、RBFNN和AWNN可达性实验结果 表2表明:AWNN的训练成功率(60%)最高,即算法可达性最好;RBFNN的训练成功率为40%;而BPNN实验成功率为0%,精度最差。 将训练的目标误差err_goal减小至0.03和0.02时,RBFNN和AWNN的训练成功率会进一步降低,但AWNN的训练成功率始终高于RBFNN。当RBFNN训练成功率降低为0%时,AWNN依然存在训练成功的情况,进一步验证了AWNN的训练成功率最高。AWNN与RBFNN均可以获得极高的训练精度,而AWNN具有训练成功率高的优势。 将AWNN应用于智能视频分析实验[17],验证AWNN算法的特性。该实验分为两个大步骤,即视频处理和视频分析。前者包括6个子步骤:对时间序列图像的预处理、背景更新、背景差分、图像分割、标准化、二值化;后者包括两个子步骤:特征提取和模式识别。整个过程如图3所示。 Fig.3 Process of video analysis图3 视频处理和分析过程 3.1标识物入侵检测分析实验设计 选取经典的数字图像入侵识别实验,进而推广到对于一般物体的入侵、识别情况,实施步骤如下: (1)训练样本和待测样本的确定。将10个数字0,1,…,9制作成为纸板,如图4所示。将这些图像进行编码,即将每个数字图像对应为一个的3×5布尔量网络。例如:用[1 1 1 1 0 1 1 0 1 1 0 1 1 1 1]表示0,用[0 1 0 0 1 0 0 1 0 0 1 0 0 1 0]表示1。 Fig.4 Images of numbers to be identified图4 待识别的数字图像 (2)BPNN、RBFNN和AWNN设置相同的算法参数。网络学习速率η=0.1;动量系数 μ=1;目标熵Et=0.01;最大训练次数epoch=10 000;选取Sigmoid函数为激励函数,Sigmoid函数参数为θ0=1,θ1=0,α=2和β=1;设置AWNN输入层和自适应层结点数M=15,隐含层结点数n=10;输出层和综合层结点数N=F=1;训练精度err_goal=0.000 1;实验重复次数case_repeat=20。 (3)视频处理速度为每秒钟处理5帧图像,当用台式计算机时,图像处理速度最高可以达到图像显示速度25帧/s,视频图像尺寸为CIF格式。 3.2实验结果分析 随机抽取标有数字的纸板移入智能监控区域,系统将检测到入侵的纸板并对数字进行识别,实验结果参见图5(a)所示。为验证AWNN算法对于细节的分辨能力,分别选取与图5(a)所示样本极其近似的样本进行实验,实验结果参见图5(b)。 Fig.5 Results of intelligent video surveillance system图5 智能视频监控系统运行示例 从图5(a)的中间窗体中可以看到,入侵的运动目标被红色方块标示出;左上角的窗体是被检测到的入侵图像区域;左下角的窗体是被检测到的区域的图像经过标准化处理和二值化处理后的结果;左侧被上述窗体遮盖的命令行窗体中显示了被检测到区域的图像经过神经网络计算的输出值,右上方窗口显示了识别的结果。 采用了AWNN算法的视频分析系统,可以完成特征相似的入侵目标侵入检测。 将上述仿真实验中的分类器算法替换为BPNN 和RBFNN算法,在不同训练精度下分别训练20次,得到的实验结果如表3所示。 Table 3 Comparison results betweenAWNN,BPNN and RBFNN video analysis application experiments表3AWNN与BPNN、RBFNN视频分析应用实验结果 从对比实验中可以看出:当目标训练误差精度较高(允许较小误差)时,BPNN始终无法完成训练,RBFNN存在较小的概率可以完成训练,而AWNN则存在较大的概率可以完成训练。即当极高精度要求时,只有AWNN可以完成训练,再次验证了AWNN具有克服局部极小点的特性,且可以获得最高精度。 将AWNN应用于智能控制实验,验证AWNN算法相对于BPNN、RBFNN算法可以使智能控制系统具有更好的特性。 神经网络控制系统结构图如图6所示。原理是在线整定器的神经网络根据系统输出量和状态量,采用梯度下降法向着输出误差最小的方向,前向计算出控制参数的更新值,新的控制参数使得在线整定器计算出最新的控制量。 Fig.6 Structure of control system图6 控制系统的结构图 在线整定器先后采用BPNN、RBFNN和AWNN算法与经典控制方法相结合,从而构成一组对比实验,即BPNN-PID、RBFNN-PID和AWNN-PID神经网络智能控制算法对比实验,从而对AWNN算法在智能控制领域应用得到的性能提升进行验证。 4.1在线整定器算法 此时其性能指标函数定义为: 选取满足框架条件的小波函数Ψa,b(t)[18]: 上述各项计算公式推导如下: 4.2计算机仿真实验 BPNN-PID、RBFNN-PID、AWNN-PID仿真程序设计方案如下:采用增量式数字PID算法作为控制器算法;采用阶跃信号rin=1作为输入;设置最大训练次数max_epoch=3 000;设置学习速率xite=0.2,惯性系数alfa=0.05。 选取最常见的二阶模型延迟环节[19]作为被控对象模型。该模型常见于液压、气动等传统控制系统中,被控对象模型为: 设计该系统为动态非线性系统,将系统内部和外部环境动态变化等价为系统输入,设置该波动起始时刻d_k=2 000,波动周期长度l_k=100。 计算机仿真结果如图7所示,对比仿真结果中的关键数据,如表4所示。 图7表明,各算法均存在收敛的可能性。其中,BPNN-PID和AWNN-PID算法实验100%收敛,而RBFNN-PID出现不收敛的情况。 表4表明:(1)AWNN-PID方法在响应快速性方面均优于BPNN-PID,RBFNN-PID方法存在不稳定的情况,但具有最快的阶跃响应速度,且是唯一出现超调的算法;(2)AWNN-PID方法的平均稳态误差小于RBFNN-PID方法,BPNN-PID方法具有最小的稳态误差;(3)各算法在非线性系统应用中,面对系统内部和外部的动态波动和扰动,各算法具有自适应跟踪与恢复能力,其中AWNN算法具有快速响应系统波动与波动后快速恢复能力,具有较好的鲁棒性。 可以得到如下结论:AWNN-PID方法具有较好的稳定性、鲁棒性,比BPNN-PID方法具有更好的响应速度。RBFNN-PID方法不稳定,不建议将没有稳定性保证机制的RBFNN-PID方法应用于工程实践。 Fig.7 Simulation results of output and error of 3 kinds of control systems图7 3个控制系统输出和误差的仿真结果 Table 4 Key data in comparative simulation results of dynamic nonlinear systems between different methods表4 不同算法在动态非线性系统中仿真对比实验结果的关键数据 AWNN算法结合了小波变换、BPNN、RBFNN算法的优点:继承了BPNN的优点,具有更好的快速收敛性;继承了RBFNN的优点,可以克服局部极小问题;继承了小波分析的优点,具有更高的分辨精度。对比实验验证了AWNN算法可以通过多次重新训练,更高概率地得到更高的精度。 当BPNN、RBFNN、AWNN分别应用于智能视频监控系统,均可实现对带有标准数字的纸板进行入侵检测、处理、分析识别功能。通过对比实验,验证了AWNN算法在训练效率、训练成功率和精度方面具有更好的特性。特别是在高精度实验中,BPNN无法完成神经网络的训练,RBFNN的训练成功率也无法达到AWNN的水平。AWNN算法和系统可以应用到家居、提款机和博物馆等智能监控领域。 BPNN、RBFNN、AWNN可以分别与经典控制算法相结合,从而构成了BPNN-PID、RBFNN-PID、AWNN-PID智能控制系统,通过算法对比实验,验证了AWNN-PID控制系统可以100%收敛,并获得理想的动态特性和鲁棒性,具有工程应用的可靠性。该方法可以应用于解决“中国制造2025”与“工业4.0”战略中涉及的系统智能化方面的前沿探索性问题。 References: [1]Silver D,Huang A,Chris J,et al.Mastering the game of go with deep neural networks and tree search[J].Nature,2016, 529:484-489. [2]Mnih V,Kavukcuoglu K,Silver D,et al.Human-level control through deep reinforcement learning[J].Nature,2015, 518:529-533. [3]Liu Chunxia,Shu Tong,Chen Shou.An improved grey neural network model for predicting transportation disruptions[J]. Expert Systems withApplications,2016,45:331-340. [4]Wang Ershen,Li Xingkai,Pang Tao.A particle filtering algorithm based on the BP neural network[J].CAAI Transactions on Intelligent Systems,2014,9(6):709-713. [5]Zhang Jiangbin,Deng Zhaohong,Wang Shitong.Radial basis function neural network modeling using fuzzy subspace clustering[J].Journal of Frontiers of Computer Science and Technology,2015,9(12):1513-1522. [6]Han Honggui,Qiao Junfei,Bo Yingchun.On structure design for RBF neural network based on information strength[J]. ActaAutomatica Sinica,2012,38(7):1083-1090. [7]Daubechies I.Ten lectures on wavelets[M].Philadelphia,USA: SIAM Press,1992. [8]Li Gang,Xu Pengcheng,Han Longmei.Fault spatial-temporal detecting and diagnosis for power grid based on wavelet analysis[J].Journal of System Simulation,2015,27(12): 3018-3024. [9]Kreinovich V,Sirisaengtaksin O,Cabren S.Wavelet neural networks are asymptotically optimal approximators for functions of one variable[C]//Proceedings of the 1994 IEEE International Conference on Neural Networks,IEEE World Congress on Computational Intelligence,Orlando,USA, Jun 27-Jul 2,1994.Piscataway,USA:IEEE,1994:299-304. [10]Wang Pu,Liu Jingwei,Li Huimin,et al.Adaptive wavelet neural network based anomaly detection and fault diagnosis classification system and method:China,ZL201110023943.2 [P].2012-08-30. [11]Li Baojian,Cheng Chuntian.Monthly discharge forecasting using wavelet neural networks with extreme learning machine[J].Science China-Technological Sciences,2014,57 (12):2441-2452. [12]Loussifi H,Nouri K,Braiek N B.Anew efficient hybrid intelligent method for nonlinear dynamical systems identification:the wavelet kernel fuzzy neural network[J].Communications in Nonlinear Science and Numerical Simulation, 2016,32:10-30. [13]Huang Ping,Yuan Xiao.Solving algorithm and program for band scaling computing of common wavelet[J].Journal of Chengdu University of Information Technology,2011,26 (2):144-145. [14]Li Yang.Research on wavelet process neural network correlative theory and its application[D].Harbin:Harbin Institute of Technology,2008. [15]Huang Tongcheng.Research on VOCR and HOCR Technology based on wavelet neural network theory[D].Shanghai: Shanghai University,2008. [16]Feng Zaiyong.Comparative study and application research between wavelet neural network and BP neural network[D]. Chengdu:Chengdu University of Technology,2007. [17]Xu Zhiwen,Guo Xiaoxin,Pang Yunjie,et al.Design and realization of network surveillance system Based on streaming media[J].Chinese Journal of Scientific Instrument,2004,25 (S2):304-307. [18]Chen Zhe,Feng Tianjin.The application of wavelet neural network for time series prediction and system modeling based on multi resolution learning[C]//Proceedings of the 1999 IEEE International Conference on System,Man and Cybernetics,Tokyo,Japan,1999.Piscataway,USA:IEEE, 1999:425-430. [19]Tajjudin M,Rahiman M H F,Ishak N,et al.Comparison between optimally-tuned PID with self-tuning PID for steam temperature regulation[C]//Proceedings of the 2012 4th International Conference on Intelligent and Advanced Systems, Kuala Lumpur,Jun 12-14,2012.Piscataway,USA:IEEE, 2012:551-556. 附中文参考文献: [4]王尔申,李兴凯,庞涛.基于BP神经网络的粒子滤波算法[J].智能系统学报,2014,9(6):709-713. [5]张江滨,邓赵红,王士同.模糊子空间聚类的径向基函数神经网络建模[J].计算机科学与探索,2015,9(12):1513-1522. [8]李刚,许鹏程,韩龙美.基于小波分析的电力系统故障时空检测与诊断[J].系统仿真学报,2015,27(12):3018-3024. [10]王普,刘经纬,李会民,等.自适应小波神经网络异常检测故障诊断分类系统及方法:中国,ZL201110023943.2[P]. 2012-08-30. [13]黄苹,袁晓.常见小波的尺度进制求解算法与程序[J].成都信息工程学院学报,2011,26(2):144-145. [14]李洋.小波过程神经网络相关理论及其应用研究[D].哈尔滨:哈尔滨工业大学,2008. [15]黄同成.基于小波神经网络理论的VOCR与HOCR技术研究[D].上海:上海大学,2008. [16]冯再勇.小波神经网络与BP网络的比较研究及应用[D].成都:成都理工大学,2007. [17]许志闻,郭晓新,庞云阶,等.流媒体网络视频监控系统的设计和实现[J].仪器仪表学报,2004,25(S2):304-307. LIU Jingwei was born in 1982.He received the Ph.D.degree in pattern recognition and intelligent system from Beijing University of Technology in 2014.Now he is a lecturer at College of Information,Capital University of Economics and Business.His research interests include artificial intelligence,intelligent control and intelligent system,etc. 刘经纬(1982—),男,北京人,2014年于北京工业大学获得博士学位,现为首都经济贸易大学信息学院讲师,主要研究领域为人工智能,智能控制,智能系统等。发表学术论文20余篇,参与国家自然科学基金项目等。 ZHAO Hui was born in 1988.He is a post doctor at Research Institute of Information Technology,Tsinghua University.His research interests include artificial intelligence and intelligent control of railway transportation,etc. 赵辉(1988—),男,河南人,清华大学信息技术研究院轨道交通控制技术研究中心博士后、助理研究员,主要研究领域为人工智能,轨道交通智能控制等。发表学术论文10余篇。 ZHOU Rui was born in 1983.She received the Ph.D.degree from Beijing University of Technology in 2013.Now she is an assistant professor at Beijing University of Chinese Medicine.Her research interest is process control. 周瑞(1983—),女,北京人,2013年于北京工业大学获得博士学位,现为北京中医药大学讲师,主要研究领域为过程控制。发表学术论文10余篇,主持国家基金1项,完成北京市基金2项,参与国家自然科学基金3项。 WANG Pu was born in 1962.He received the Ph.D.degree from China University of Mining and Technology in 1988.Now he is a professor and Ph.D.supervisor at Beijing University of Technology.His research interests include control science and engineering and intelligent system,etc. 王普(1962—),男,北京人,1988年于中国矿业大学获得博士学位,现为北京工业大学教授、博士生导师,主要研究领域为控制科学与工程,智能系统等。发表学术论文80余篇,承担各类科研项目50余项。 *The National Natural Science Foundation of China under Grant No.11402006(国家自然科学基金);the Science and Technology Foundation of Beijing Municipal Education Commission under Grant No.KM201610038001(北京市教委科技基金);the Project and Foundation of Capital University of Economics and Business under Grant Nos.00791554410263,00791654490210, 00791654210157(首都经济贸易大学科研启动基金、校内专项科研项目、校级教改青年项目). Received 2016-01,Accepted 2016-03. CNKI网络优先出版:2016-04-08,http://www.cnki.net/kcms/detail/11.5602.TP.20160408.1642.006.html 文献标志码:A 中图分类号:U621;TP273 doi:10.3778/j.issn.1673-9418.1602015 Exploration of High-Precision Adaptive Wavelet Neural Network Artificial Intelligence Methodƽ LIU Jingwei1,2+,ZHAO Hui3,ZHOU Rui2,WANG Pu2 Abstract:In order to solve the accuracy problem and the requirements of artificial intelligence systems,this paper proposes an adaptive wavelet neural network(AWNN)method,which is combined with the advantages of wavelet analysis method,BP(back propagation)and RBF(radial basis function)neural network.Then,this paper uses AWNN into intelligent video analysis and intelligent control system,and verifies better convergence and high accuracy of AWNN. Firstly,AWNN is analyzed theoretically and a group of comparative simulation experiments are implemented to verify that AWNN can improve speed and precision.Secondly,AWNN based intelligent video analysis systems are imple-mented to verify that AWNN has more accurate content classification ability.Finally,AWNN based intelligent control systems are implemented to verify thatAWNN has better control features. Key words:wavelet neural network;intelligent system;video analysis;intelligent control system;neural network control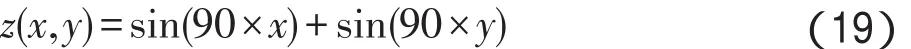



3 AWNN智能视频分析系统应用研究
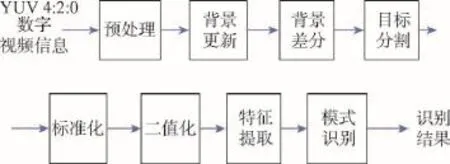


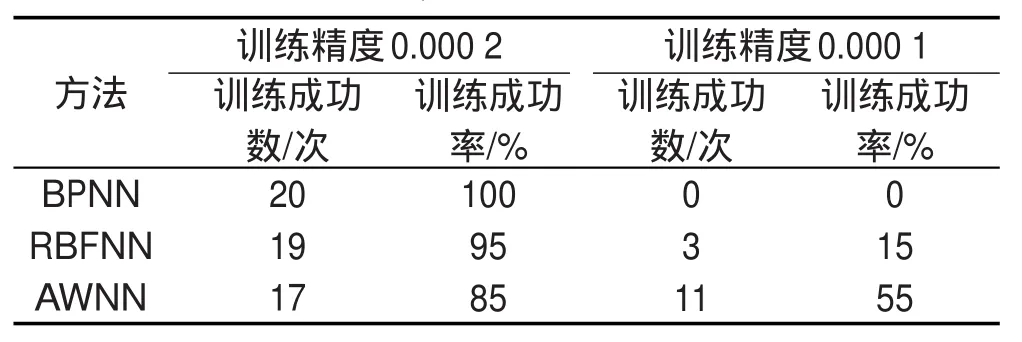
4AWNN智能控制系统应用研究
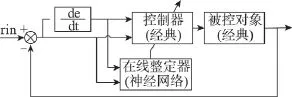


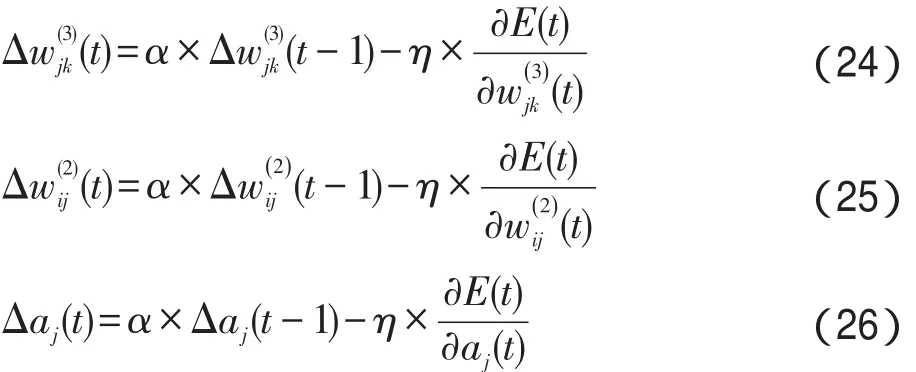
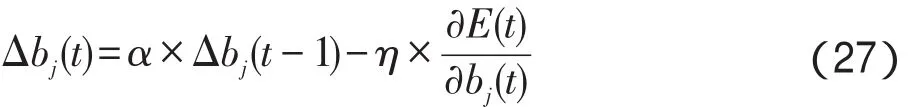
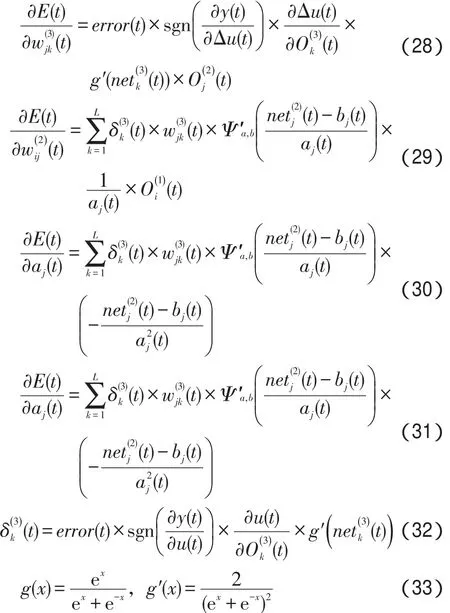


5 结论与展望




1.College of Information,Capital University of Economics and Business,Beijing 100070,China
2.College of Electronic Information and Control Engineering,Beijing University of Technology,Beijing 100124,China
3.Research Institute of Information Technology,Tsinghua University,Beijing 100084,China
+Corresponding author:E-mail:liujingwei@cueb.edu.cn
