离散小波变换在医学图像中的应用

韩宝如， 林尔敏*（海南软件职业技术学院，海南琼海，571400）



离散小波变换在医学图像中的应用

韩宝如， 林尔敏*
（海南软件职业技术学院，海南琼海，571400）

本文以三维医学体数据作为研究对象，充分利用离散小波变换，对其进行多分辨率分解，把三维医学体数据分解成三个不同方向上的子医学体数据。实验结果表明，三维医学体数据经过离散小波变换后被分割成八个子频带，其主要能量和特征集中在低频子带系数中，可以用来提取特征向量构造零水印。

离散小波变换；三维医学体数据；多分辨率分解

0 引言

小波变换是一门新兴学科，自提出以来，小波分析理论、方法与应用的研究一直处于快速的发展中。小波变换能够依据信号分析的需要，进行信号的局部化分析。这是因为它拥有随着频率变化的“时间-频率”窗口。经过这些多年的发展，小波变换的研究与应用，已经吸引了越来越多研究人员极高的关注，目前已经是国际研究人员研究的热点问题。小波变换的应用领域非常广阔，已经应用到科学研究的许多方面。例如信号处理、图像和视频分析与处理、、理论物理、量子力学、机器视觉、语音信号处理、医学图像处理、故障诊断和地质数据处理等方面。

小波变换具有多分辨率分析的特点，避免了短时傅立叶变换在单分辨率上的缺点。它的“时间-频率”窗口可以依据信号的具体形式和要求进行变化。因此在时域和频域都有表征信号局部信息的能力。在一般情况下，为了提高频率的分辨率，在低频部分（信号较平稳）可以采用较低的时间分辨率。为了获得确的时间定位。通常在高频情况下（频率变化不大）采用较低的频率分辨率。由于具有这些特点，所以小波变换可以检测正常信号的瞬态，并能把其频率成分显示出来，故被叫做数学显微镜。

为了计算离散的位移和尺度，把连续小波离散化，叫做离散小波变换。即只对连续伸缩因子与平移因子进行离散化，时间变量并不进行离散化。

1　一维离散小波变换

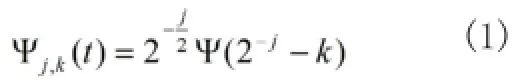
则其变换系数是：

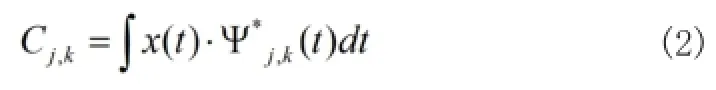
其重构公式是：

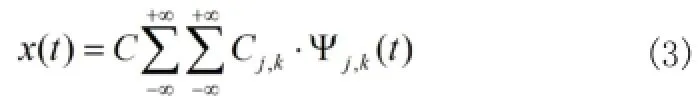
式中C是常数，与信号无关。

所以一维离散小波变换是：

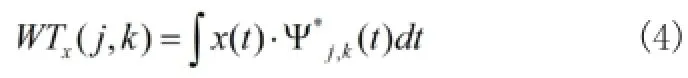
其逆变换是：

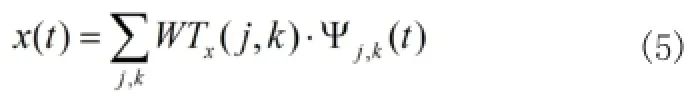
① 线性

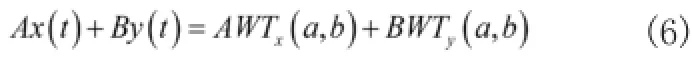
式中，A，B 为任意的实常数。

② 移位不变性

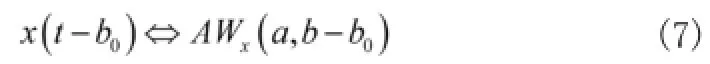
③ 尺度变换性

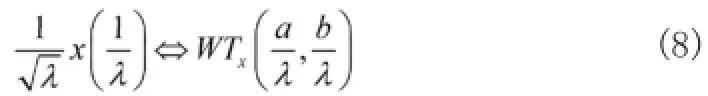
④ 能量守恒定律

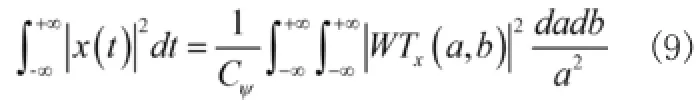
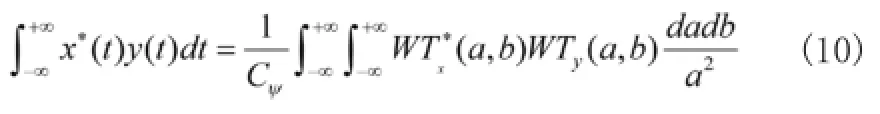
⑤ 相似性与消失矩

通过伸缩参数和平移参数，一个小波能够得到一个小波族，且它们彼此自相似，这通常要求小波有消失矩的特性：

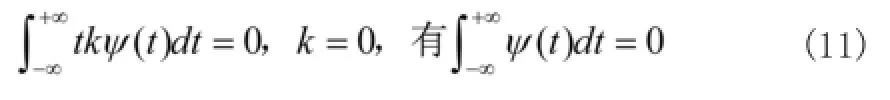
2　二维离散小波变换

根据一维离散小波变换，推广到二维离散小波变换。在二维离散小波变换情况下，令为二维尺度函数，只讨论尺度函数是可以分离的情况，有：

利用二维离散小波变换首先对图像进行变换，其变换的本质是多分辨率的分解，具体而言就是对图像的不同频率和空间进行分解，这些频率和空间都有其对应的子图像，子频带我们用LL来表示低频的子带，同样，HL、LH和HH分别是水平子带、垂直子带和对角子带（这四个大写字母组合都是指代频率，其主要区别在于中首字母是水平方向，而第二个字母则是垂直方向）。如果继续对其进行二维离散小波变换则在左上角的LL低频子带继续按照上面的方式进行，以此类推。二维离散小波分解如图1所示。

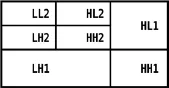
图1　小波分解

3　三维离散小波变换

利用三维离散小波变换对三维体数据进行变换，即对体数据做多分辨率分解，将体数据分解成X，Y，Z不同方向上的子体数据，经过变换后，体数据被分割成八个频带。三维离散小波变换的一层分解如图2所示。

图2　三维离散小波变换的一层分解

通过低频和高频滤波后得到的体数据的高频成分和低频成分，分别用L和H表示。利用三维离散小波变换对体数据变换后，体数据被分解成低频三维子带及高频三维子带，前者是代表体数据低频特性的“近似系数”LLL1，后者即为代表此体数据高频信息的“细节系数”，下标“1”用来表示此为DWT的第一层分解。

4　实验

对一个医学图像进行二维离散小波变换， 其一级分解后的图像如图3所示。从图3中可看出，医学图像的大部分能量集中在低频子带LL，它被叫做原始医学图像的逼近子图。其它三个子带具有原医学图像的水平边缘细节、垂直边缘细节和对角边缘细节，代表细节特性，被称作细节子图。

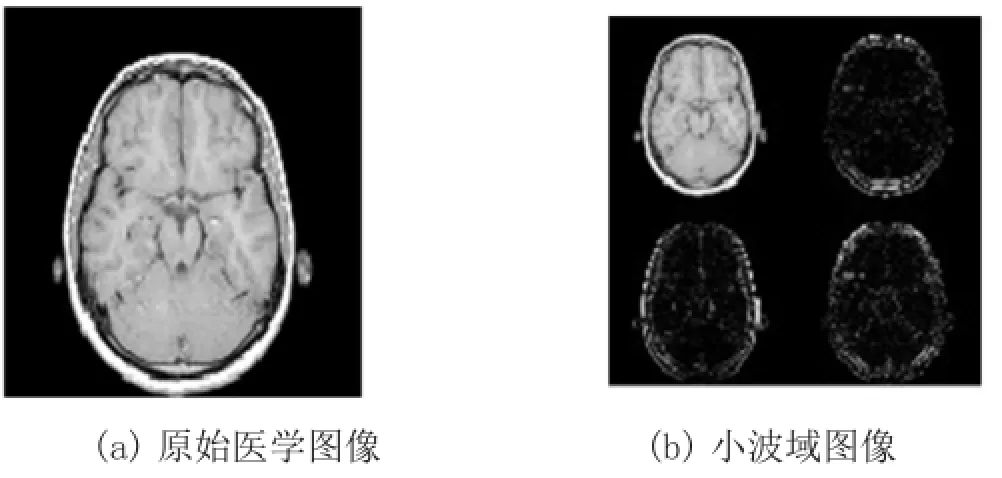
图3　医学图像的离散小波变换

对肝医学体数据进行三维离散小波变换（一层）后的结果如图5所示。

从图4和图5可以看出，对于三维医学体数据而言，通过离散小波变换，就是体数据进行多分辨率分解，把图像分解成X，Y，Z不同方向上的子图像。三维数字体数据经过小波变换后被分割成八个频带。从图中可以看出，三维医学体数据的主要能量和低频特征集中在低频系数中。

5　结论

本文首先介绍了小波变换的发展、特点和应用。其次详细介绍了离散小波变换的定义和性质。并利用离散小波变换对二维医学图像和三维医学体数据进行了分解，效果非常好。因此离散小波变换在医学图像中的应用越来越广泛。

［1］ 李京兵，杜文才. 二维和三维医学图像稳健数字水印技术［M］.北京：知识产权出版社， 2012.

［2］ Baoru Han， Jingbing Li. Application of chaotic neural network and 3D DWT-DFT in medical volume data watermarking［C］. ITMI2013， 2013， 1209-1212

［3］ 侯艳芹， 李均利， 魏平等. 一种基于二维离散小波变换的医学图像增强算法［J］. 计算机工程与应用， 2006，42（7）：227-229.

［4］ 杨小帆， 黄向生， 何中市，等. 离散小波变换图像压缩技术综述［J］. 计算机科学， 2002， 29（5）：110-111.

［5］ 王向阳， 杨红颖. 一种基于离散小波变换的图像数字水印算法［J］. 微型机与应用， 2003， 22（2）：50-52.

林尔敏 ：通信作者

Discrete wavelet transform in medical image application

Han Baoru，Lin Ermin*
（Hainan Software Profession Institute， Hainan， Qionghai，571400）

In this paper，the three-dimensional medical volume data is used as the object of study，and the discrete wavelet transform is used to decompose the three-dimensional medical volume data.Threedimensional medical volume data is decomposed into three sub medical data in different directions.The experimental results show that the three-dimensional medical volume data is divided into eight subbands by discrete wavelet transform.And the main energy and features are concentrated in the low frequency subband coefficients，which can be used to extract feature vectors to construct zero-watermarking.

Discrete wavelet transform；three-dimensional medical volume data；multi-resolution decomposition

海南省高等学校科学研究项目（Hnky2015-80）

韩宝如（1982-），男，山东临沂人，副教授，在读博士研究生，主要从事数字水印，通信技术研究；