基于预紧轴承动刚度的高速电主轴动特性分析*

崔　立

(上海第二工业大学工学部，上海 201209)



基于预紧轴承动刚度的高速电主轴动特性分析*

上海市自然科学基金项目(14ZR1416800)；上海市联盟计划项目(LM201408)；国家自然科学基金资助(51305251、50905061)；上海第二工业大学重点学科“材料与工程”(XXKZD1601)

崔立

(上海第二工业大学工学部，上海 201209)

针对定位预紧的电主轴球轴承，基于球和套圈相互作用模型，推导了球轴承刚度求解模型，使用Newton-Raphson方法求解可到刚度矩阵。基于Riccati传递矩阵法，给出了考虑轴承动刚度的电主轴临界转速计算方法。建立了铣削激振下考虑轴承动刚度的电主轴动力学方程，使用Runge-Kutta法求解得到电主轴动力学响应。对某铣削高速电主轴计算，结果发现轴承径向刚度随转速增大而减小，采用定位预紧后刚度增大，且随转速增大轴心预紧刚度增大明显。考虑轴承动刚度可得到更为准确的电主轴动特性结果，最后通过高速电主轴动特性实验证明了该模型对动特性预测的准确性。

高速电主轴；动刚度；球轴承；动态特性；临界转速

电主轴的动态特性指它抵抗受迫及自激振动的能力。动态特性包括固有振动特性和响应特性，这些特性对机床加工性能的影响很大，不仅影响机床的加工精度、使用寿命，也影响着其高效率性能的发挥。

为提高电主轴的精度，主轴上使用的滚动轴承需预紧，轴承预紧后各滚动体受力将更加均匀，可提高抗振性。目前关于考虑轴承预紧，研究电主轴性能的研究已有不少。Alfares等[1]建立了电主轴的五自由度动力学方程，分析了轴承预紧力对电主轴动力学性能影响，结果表明随着初始预紧力的增大主轴的振动量减小，但预紧力增大到一定程度时，主轴的振动将不再明显减小。Lin等[2]研究了在超高速情况下电主轴的动力学特性，轴承预紧力对轴承刚度与主轴动力学的影响，高转速对轴承球离心力、陀螺力矩，进而分析了对主轴整机动力学的影响。Kang等[3]用有限元法，使用Ansys软件分别完成机床主轴轴承系统静态、动力学特性与机床的颤振分析。赵志刚等[4]基于Ansys软件对电主轴转子轴承系统进行了动静态性能分析，给出了轴承位置及跨距对电主轴动特性影响。李松生等[5-6]用有限元法，建立了高速电主轴轴系转子动力学模型，分析了轴承支承特性随速度变化的非线性特性和电主轴固有频率。邱海飞等[7]设计了电主轴动力学试验台，确定了不同转速段轴承最小预紧力。以上这些研究中，研究了预紧力对电主轴动特性的影响，但未考虑预紧作用下轴承动刚度的影响。

本文提出了考虑轴承动刚度的电主轴动特性计算方法，给出了电主轴临界转速和动态响应的计算方法，通过对高速电主轴动特性测试验证模型的可靠性。

1　考虑动刚度的电主轴临界转速分析

1.1考虑预紧的轴承刚度模型

轴承预紧方式有定位预紧和定压预紧。由于定位预紧方式对增加轴承刚度更为有效，所以定位预紧广泛应用于大功率高速机床主轴上。

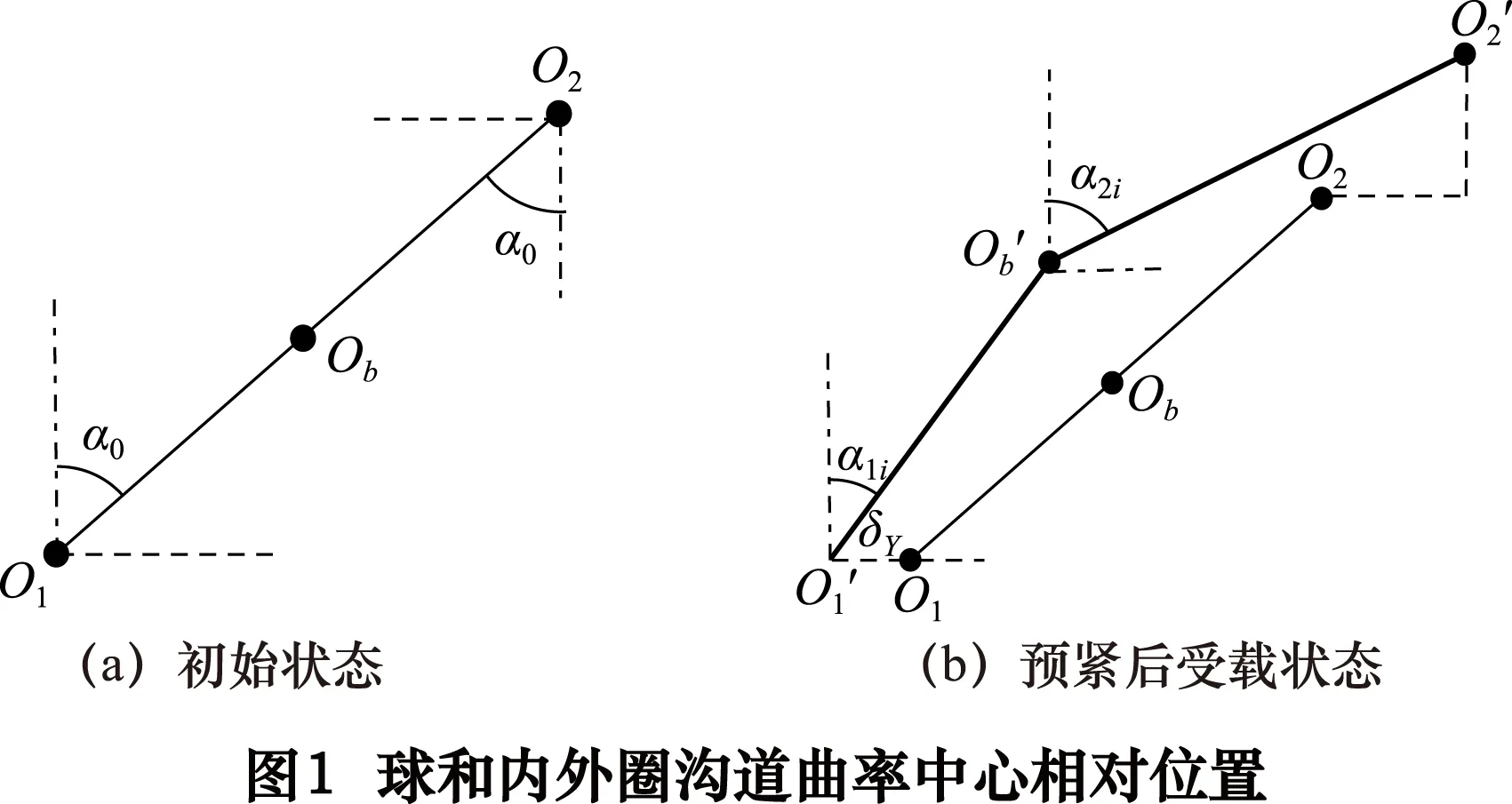
图1a为球轴承初始状态时球和内外圈沟道曲率中心相对位置，内外圈沟道的曲率中心分别为O2和O1，球的曲率中心为Ob，初始接触角为α0。在外圈受到定位预紧作用下，外圈曲率中心从O1移动到O1′，假设球轴承工作时受轴向载荷和径向载荷作用，图1b为受载状态下，外圈曲率中心不变，内圈曲率中心沿轴向和径向移动到O2′，球的曲率中心移动到Ob′，α1i、α2i分别为受载后第i个滚动体与外圈、内圈的接触角。

-(f1-0.5)Dw

(1)

-(f2-0.5)Dw

(2)

(3)

(4)

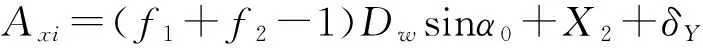
由赫兹接触理论[8-9]可求得球和外圈、内圈的接触力Q1i、Q2i。

假设轴承所受载荷[Fi]={Fx,Fy,Fz}，建立球和内圈的力平衡方程可得：

Q1isinα1i= Q2isinα2i

(5)

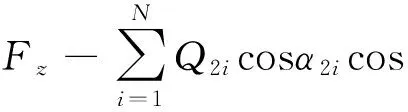
式中：ωoi是第i个球的公转转速，采用Newton-Raphson方法求解非线性方程组。轴承刚度可得

(6)

式中：Kb为刚度矩阵，求解方程组得到的雅可比矩阵即为轴承刚度矩阵。

1.2考虑动刚度的电主轴临界转速计算

电主轴实际工作过程中应避开临界转速，因此应计算出电主轴的临界转速。而电主轴运转过程中由于轴承刚度会发生变化，为准确计算电主轴临界转速，应该考虑轴承动刚度进行计算。本文采用求解快速且精度较高的传递矩阵法。

将电主轴轴承系统划分为若干杆单元和节点，建立动力学方程如下：

(7)

式中：u为节点位移矩阵；M为质量矩阵；C为阻尼矩阵；G为陀螺力矩阵；F为载荷矩阵；Ks为转轴刚度矩阵[10]，Kb为轴承刚度矩阵。

电主轴运转过程中，当轴承转速或所受载荷变化时轴承刚度也将发生变化，因此应考虑动刚度，联立式(6)与式(7)，使用Riccati传递矩阵法[10]求解可得到系统的频率方程式：

(8)

式中：S为电主轴的Riccati传递矩阵。使用Newton-Raphson方法求解式(8)可得各阶特征值：

s=λj+iωj

(9)

式中：λj为衰减因子；ωj为固有频率。

在电主轴转速范围内计算系统的特征值，得到固有频率，当固有频率与电主轴转速相等时，即为电主轴临界转速。

2　考虑动刚度的电主轴响应分析

铣床电主轴的激振力主要来自于铣刀的铣削力，圆柱铣刀的平均圆周切削力公式为：

(10)

式中：CF为铣削材料系数；ae为铣削深度；af为每齿进给量；dq为铣刀直径；ap为铣削宽度；Z为铣刀齿数。

铣削激振力可写为：

q(t)=Fqcos(ωqt)

(11)

式中：ωq为激振力频率，ωq=Zω；ω为轴频。

铣削激振力是周期性的激振力，为分析铣削激振力作用下的动态响应，将式(11)中的铣削激振力g(t)替代式(7)，联立式(5)求解轴承动刚度矩阵Kb。使用Runge-Kutta法求解式(7)，得到电主轴各节点的动力学响应。

3　电主轴动态性能分析与实验

3.1电主轴临界转速分析

以图2所示的铣削电主轴为例进行分析，电主轴总长度为550 mm，前支承轴承采用3个型号相同的角接触球轴承7014，后支承轴承采用两个型号相同的角接触球轴承7010，前后支承轴承都采用定位预紧，电主轴最高工作转速为18 000 r/min。

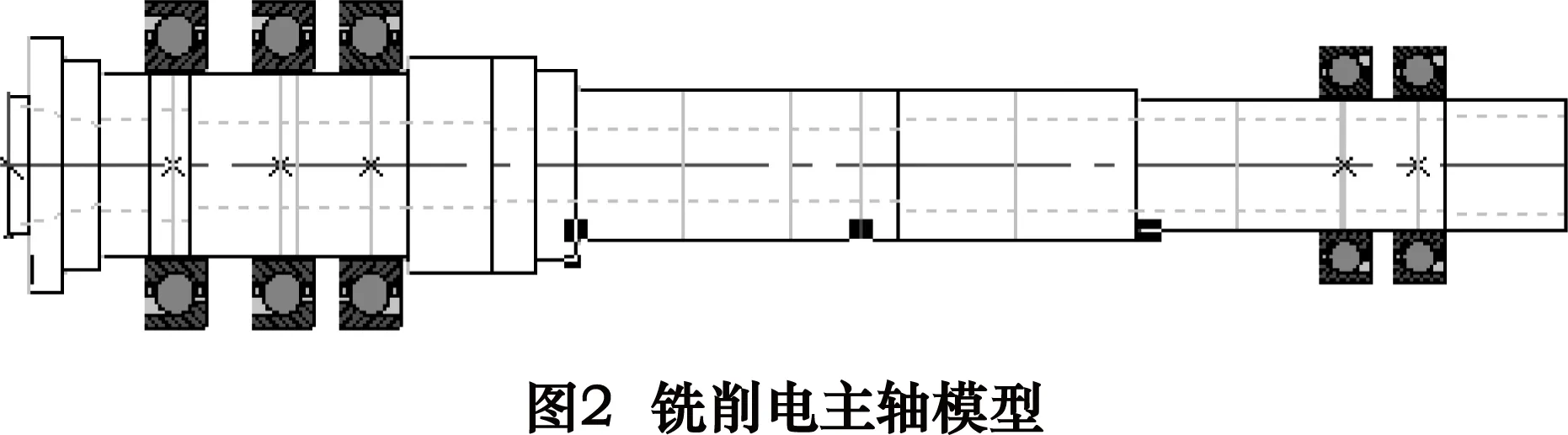
对前支承轴承7014进行刚度计算。图3给出了在电主轴最高转速18 000 r/min时，前支承轴承刚度随预紧量变化曲线。可以看出轴向刚度和径向刚度均随预紧量增大而增大，但增大幅度随预紧量增大逐渐减小。考虑到高速电主轴发热量随预紧量增大也会逐渐增大，选取较轻预紧，预紧量为10 μm。

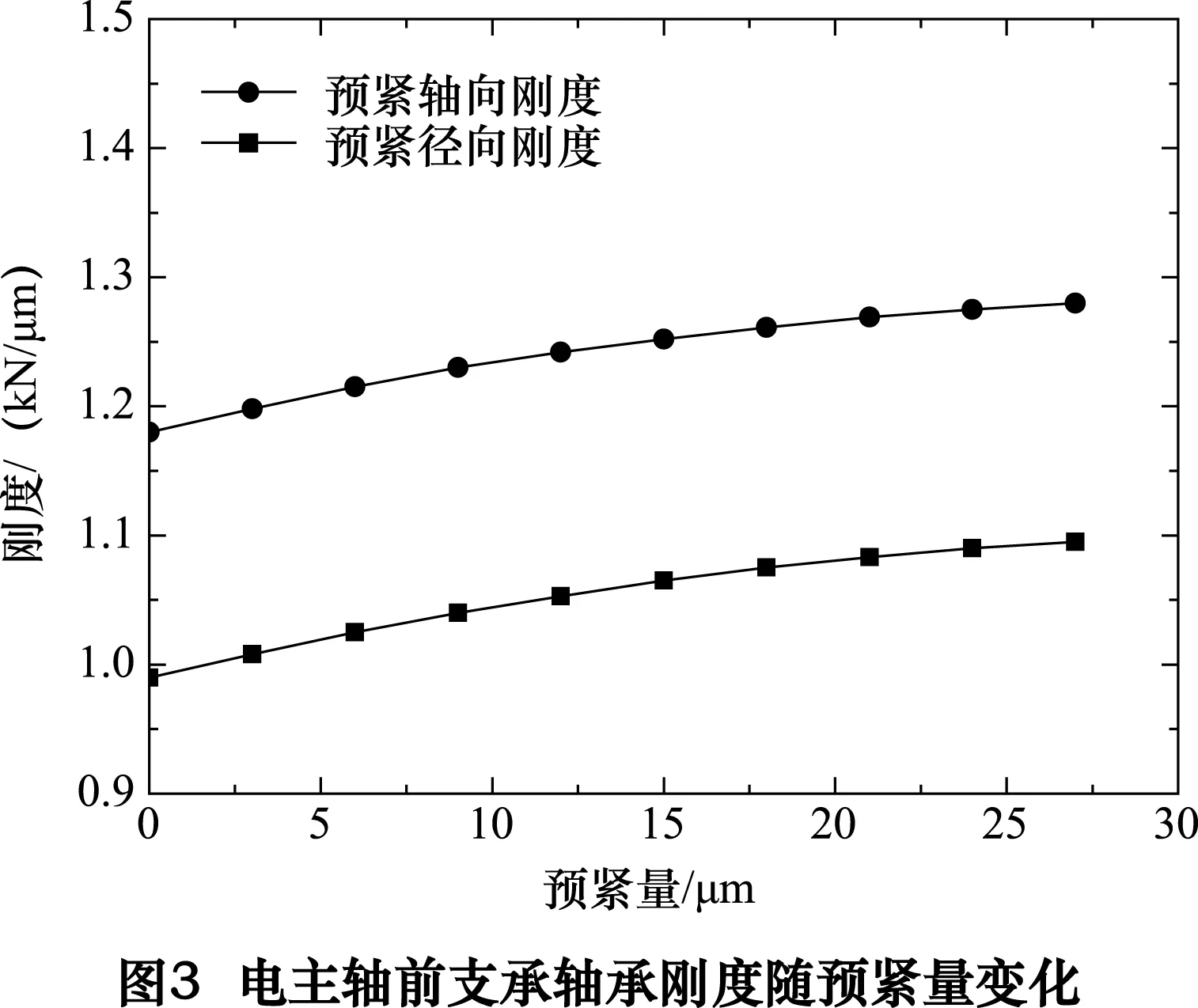
当定位预紧为10 μm时，图4给出了在联合载荷作用下球轴承径向刚度随随转速增大呈非线性减小，轴向刚度随转速增大而增大。轴承采用定位预紧后，轴向和径向刚度与没有预紧相比均增大，且随转速增大预紧刚度的增大更加明显。

使用本文给出的动刚度方法计算电主轴固有频率，同时与不考虑动刚度方法计算对比，图5给出了电主轴的一阶、二阶临界转速计算结果对比，图中虚线为同步激励线，同步激励线与各固有频率曲线的交点即为电主轴的各阶临界转速。

可以看出，考虑动刚度计算得到的电主轴临界转速为22 500 r/min、31 500 r/min，而不考虑动刚度计算得到的电主轴临界转速则为25 000 r/min、38 000 r/min，两种计算方法得到的一阶和二阶临界转速差别分别为11.1%和20.6%，这是由于轴承刚度随转速增大而改变，引起临界转速值的改变。

3.2电主轴动态响应分析

CF取68．2，铣削深度ae取2 mm，每齿进给量af取0.2 mm，铣刀直径dq取32 mm，铣削宽度ap为25 mm，铣刀齿数Z为4。在最大转速18 000 r/min时，铣削激振力为：q(t)=1935cos(1200t)，将电主轴划分为10个节点，求电主轴各节点位移响应。

图6为考虑动刚度和未考虑动刚度时，电主轴各节点位移响应最大值曲线，可看出最大位移在电主轴前端，考虑动刚度和未考虑动刚度时最大位移分别为19 μm和15 μm，未考虑动刚度时电主轴位移响应整体偏小。

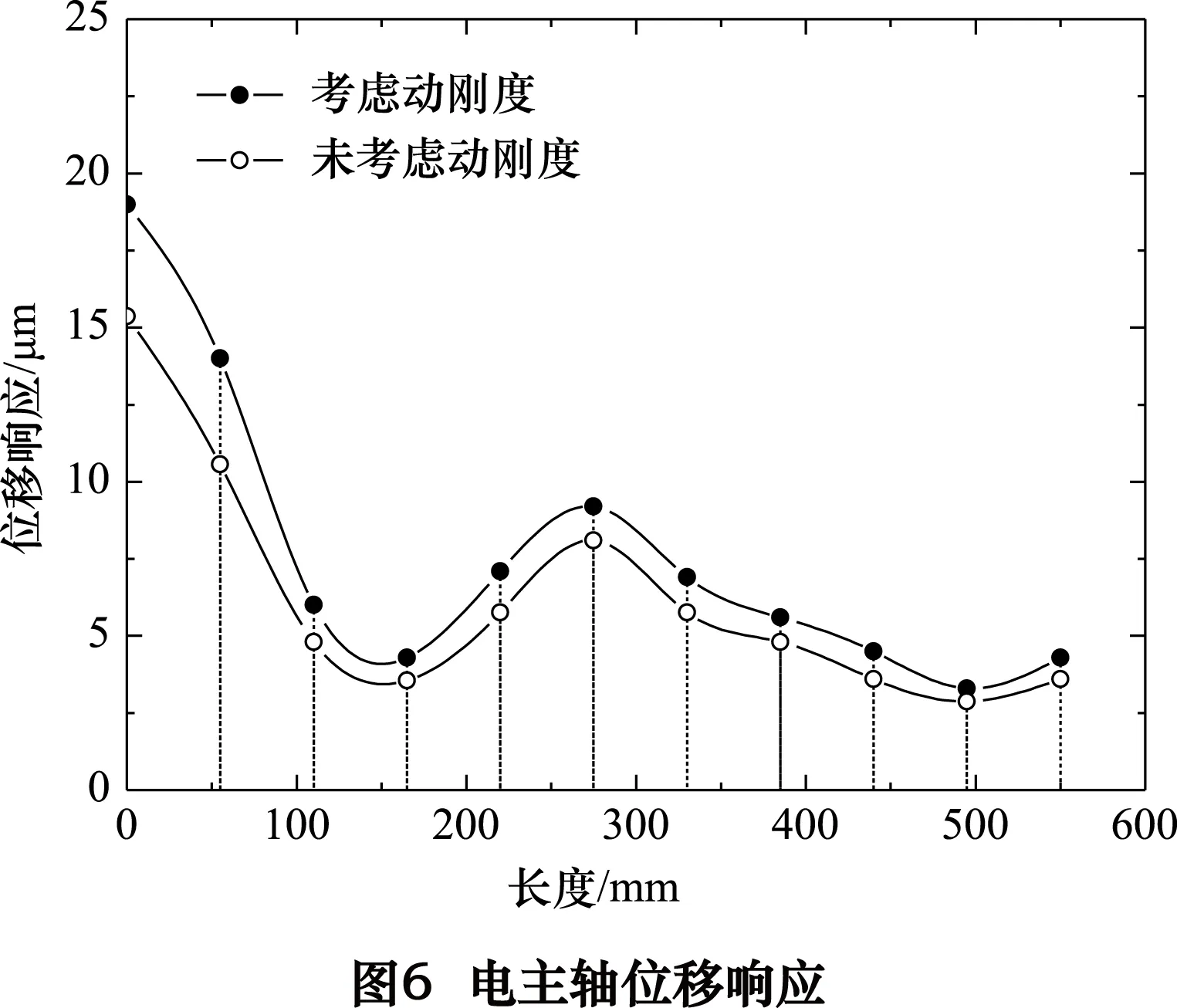
3.3电主轴动态特性实验

在自主开发的高速大功率电主轴实验台上测试，实验台包括电主轴、变频器、水冷装置、空气压缩机，以及温度、振动、位移、LMS数据采集等测试系统。图7是电主轴性能测试实验台，电主轴最高转速18 000 r/min，功率45 kW，支承轴承为角接触球轴承，预紧量为10 μm。

使用该实验台进行高速电主轴前端振动位移测试，转速测试范围为2 000 r/min到18 000 r/min，加载转矩20 N·m，图8为电主轴前端位移实验结果和计算结果对比，随转速增大振动位移逐渐增大，考虑动刚度计算与测试结果较为接近，高速时有一定误差，是由于电主轴内部零件存在不平衡量导致的振动，实验结果验证了文中方法的可靠性。

4　结语

建立了考虑预紧的球轴承刚度求解模型，基于Riccati传递矩阵法，给出了考虑轴承动刚度的电主轴临界转速计算方法和动特性计算方法，对某高速电主轴动特性进行了分析，得到如下结果：

(1)球轴承径向刚度随转速增大而减小，轴向刚度随转速增大而增大，采用定位预紧后，轴向和径向刚度与没有预紧相比均增大，且随转速增大预紧轴向刚度增大更加明显。

(2)考虑滚动轴承的动刚度计算转子系统的临界转速，与定刚度值计算相比有较大差别，为准确计算电主轴临界转速应考虑动刚度。

(3)实验验证了考虑轴承动刚度可得到更为准确的电主轴动特性结果，为电主轴动态特性的准确分析提供了方法。

[1]Mohammed A Alfares, Abdallah A Elsharkawy. Effects of axial preloading of angular contact ball bearings on the dynamics of a grinding machine spindle system[J]. Journal of Materials Processing Technology, 2003,136: 48-59.

[2]Lin Chi-wei, Tu Jay F, Kamman Joe. An integrated thermo mechanical dynamic model to characterize motorized machine tool spindles during very high speed rotation[J]. International Journal of Machine Tool & Manufacture, 2003, 43: 1035-1050.

[3]Kang Y, Chang Y P. Integrated CAE strategies for the design of machine tool spindle-bearing systems[J]. Finite Elements in Analysis and Design,2001, 37: 485-511.

[4]赵志刚, 巫少龙. 基于ANSYS的机床电主轴动态性能分析[J]. 制造技术与机床, 2010(8): 149-152.

[5]李松生，杨柳欣，王兵华.高速电主轴轴系转子动力学特性分析[J].轴承, 2002(2):15-17.

[6]李蓓智，吴喜如，杨建国．精密数控车床电主轴一轴承-转子系统动态性能计算分析[J]．机械设计与制造，2010(3): 173-175．

[7]邱海飞. 高速陶瓷电主轴动力学特性研究[J]. 制造技术与机床, 2014(12): 101-107.

[8]Harris T A. Rolling bearing analysis[M]. New York: Wiley, 2009.

[9]王黎钦，崔立，郑得志. 航空发动机高速球轴承动态特性分析[J]. 航空学报, 2007, 28(6): 1461-1467.

[10]闻邦椿. 高等转子动力学-理论、技术与应用[M]. 北京：机械工业出版社, 2000.

(编辑李静)

(收修改稿日期：2016-05-11)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Dynamic characteristics analysis of high speed motorized spindle based on dynamic stiffness of rolling bearing with preload

CUI Li

(Faculty of Engineering, Shanghai Polytechnic University, Shanghai 201209, CHN)

For spindle bearings with position preload, bearing stiffness model is presented based on the interactions model between the ball and rings. Newton-Raphson method is used to solve the stiffness matrix. Based on Riccati transfer matrix method, calculation method of critical speed of motorized spindle considering the dynamic stiffness of bearing is presented. The dynamic equation of the motorized spindle considering dynamic stiffness of bearing under milling excitation is given, and the dynamic responses are solved by using Runge-Kutta method. Taking a high speed milling spindle as an example, results show that radial stiffness of the bearing decrease with increase of rotating speed, the bearing stiffness increases with the positioning preload, and the increase becomes obvious with the increases of speed. More accuracy of dynamic responses of the spindle system can be obtained by considering dynamic stiffness. Finally the dynamic characteristic experiment of high-speed electric spindle demonstrates the accuracy of the proposed model.

high speed motorized spindle; dynamic stiffness; ball bearing; dynamic characteristics; critical speed

TH133.3

A

10.19287/j.cnki.1005-2402.2016.07.014

崔立，男，1981年生，博士，副教授，研究方向为高速轴承技术、摩擦学、转子动力学，已发表论文30余篇。

160723