几何误差对多孔质气静压轴承性能的影响*

侯晓帅　赵则祥　于贺春　张国庆　何　鑫　姚　博

(中原工学院机电学院，河南 郑州 451191 )



几何误差对多孔质气静压轴承性能的影响*

国家自然科学基金资助项目(51475485)；国家自然科学基金资助项目(51405523)；郑州市科技攻关项目(121PPTGG363-6)

侯晓帅赵则祥于贺春张国庆何鑫姚博

(中原工学院机电学院，河南 郑州 451191 )

针对几何误差对多孔质气静压轴承性能的影响，采用基于有限体积法的Fluent软件对流场进行三维建模仿真。研究了几何误差对多孔质气静压轴承承载力和刚度的影响，得到以下结论：几何误差形成的气膜间隙变化造成的压力分布不均，当中凸-直线、中凸-圆弧和圆锥度误差在3 μm以内时，对气静压轴承的性能有明显的提高；沿径向方向上倾斜3 μm以内时，对气静压轴承的性能影响不大；中凹和椭圆度误差对气静压轴承的性能有负作用。

气静压轴承；几何误差；承载力；刚度

多孔质材料作为气静压轴承的节流器具有广泛的应用范围，主要原因是多孔质材料节流器供气面积大，稳定性能好，具有较高的承载能力和刚度等优点[1]。目前，多孔质材料有青铜、不锈钢、陶瓷和石墨等。青铜和不锈钢材料的塑性较大，用机械加工方法难以获得不被堵塞的多孔质表面。经磨削加工的陶瓷孔隙内极易出现脆裂的微粒。采用冷等静压的工艺方法制造出的各向同性多孔质石墨是比较理想的材料，它不仅具备一般石墨的全部特性而且材料结构均匀且致密、孔隙分布均匀、抗氧化能力强[2]。但是多孔质石墨由于质软，加工过程中不利于保证几何精度。

吴笛[3]建立了局部多孔质气静压径向轴承的数学模型并研究了各参数对轴承静态特性的影响；李欢欢等人[4]研究了椭圆误差对多孔质气静压轴承特性的影响；李树森等人[5]理论推导了几何形误差对气静压圆柱轴承运动精度的影响关系式，提出设计时应当考虑几何误差的影响，但未给出详细的设计指导；徐建民等人[6]应用边界元法研究了在二维流动假设下，轴承副具有几何形状误差时空气静压轴承的工作特性；侯志泉[7]系统研究了工作参数和结构参数以及静压轴承摩擦副形状误差对液体静压轴承性能的影响规律；边新孝等人[8-9]考虑气膜厚度误差对小孔节流径向轴承承载能力的影响；采用数值计算的方法，分析了小孔节流径向轴承支点反力不在中点或在中点且有弯矩时偏载情况的影响；Pande S S等人[10]利用有限差分法分析了几何形误差和表面粗糙度对小孔节流径向轴承静态特性的影响；James Nevel[11]研究了定子和转子的n棱圆误差对气静压轴承性能的影响，分析了由于气膜的弹性作用弥补了n棱圆误差的缺陷，n棱圆误差对气静压轴承性能的影响可以忽略。综合国内外的研究现状，笔者通过分析几何误差形成的气膜间隙变化造成的压力分布情况，研究了多孔质气静压主轴的圆度、圆柱度和倾斜度等几何误差对气静压轴承承载力和刚度的影响。

1　模型建立

1.1物理模型的建立

建立的多孔质气静压径向轴承副模型如图1所示。设定多孔质径向轴承的主要参数如表1所示。理想状态下的具体结构参数：直径d=50 mm，长L=80 mm，单侧气膜厚度h=10 μm。

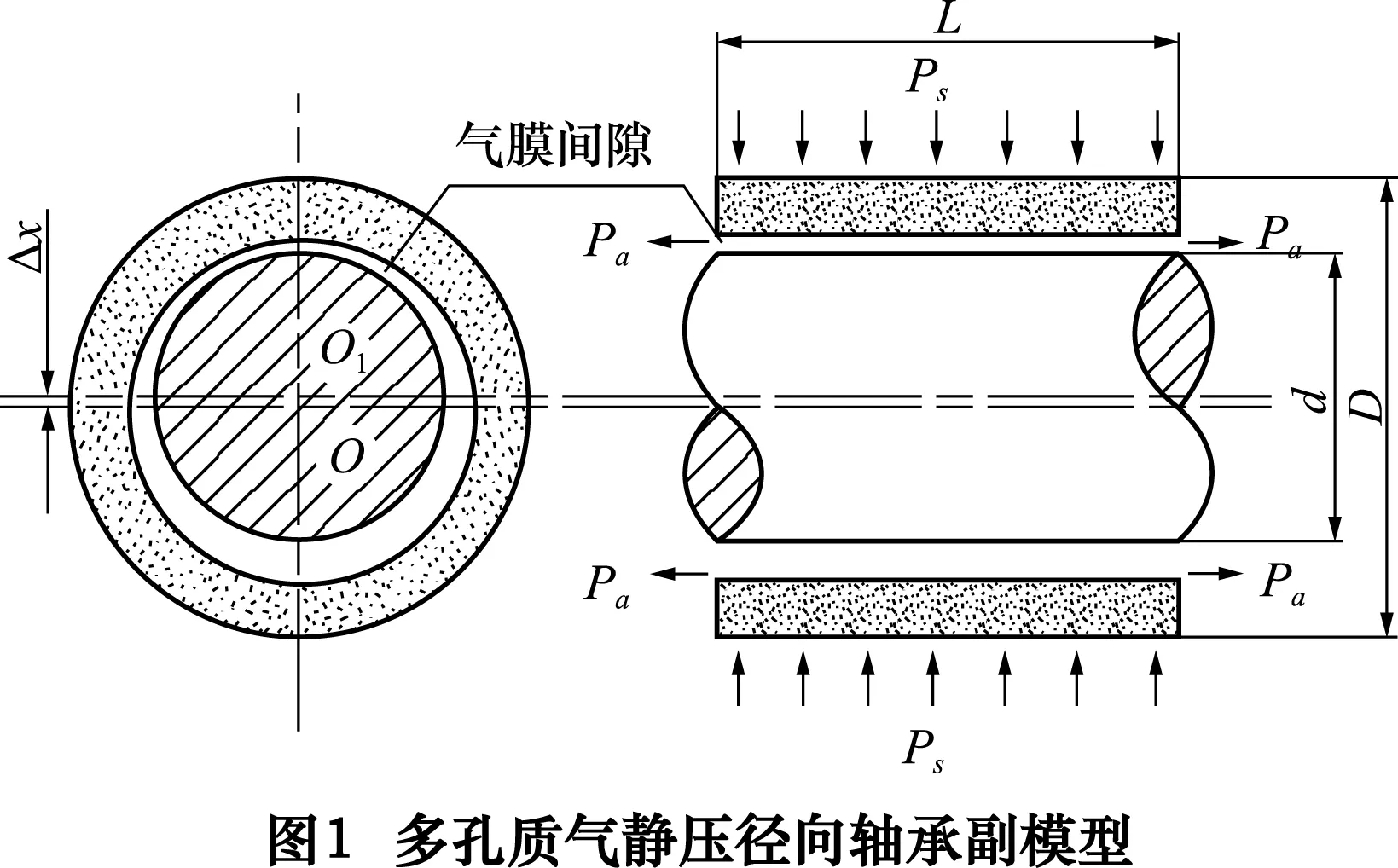
表1主要参数表

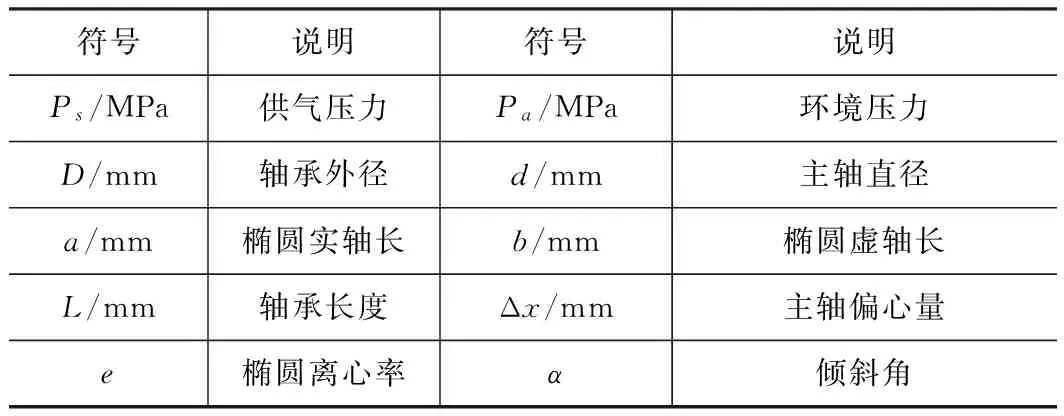
符号说明符号说明Ps/MPa供气压力Pa/MPa环境压力D/mm轴承外径d/mm主轴直径a/mm椭圆实轴长b/mm椭圆虚轴长L/mm轴承长度Δx/mm主轴偏心量e椭圆离心率α倾斜角

根据国家标准GB/T1182-2008《产品几何技术规范(GPS)几何公差 形状、方向、位置和跳动公差标注》的规定，几何误差包括形状公差、方向公差、位置公差和跳动公差。形状公差主要包括圆度和圆柱度等[12]。在实际生产中，加工出来的气静压径向轴承(孔)与其相配的轴不仅存在尺寸偏差而且存在诸如圆度、圆柱度等几何误差，造成气膜厚度在轴向和径向都是不均匀的。同时，多孔质气静压轴承与主轴在装配过程中会产生倾斜度误差。

为便于理论分析，采用简化了的主轴几何误差模型计算多孔质气静压轴承的承载力和刚度。其中简化原则是：保证不改变几何公差值的情况下，将多孔质气静压主轴表面不同波纹度的曲线通过最小二乘法拟合为直线或圆弧等形状。

1.1.1圆度误差

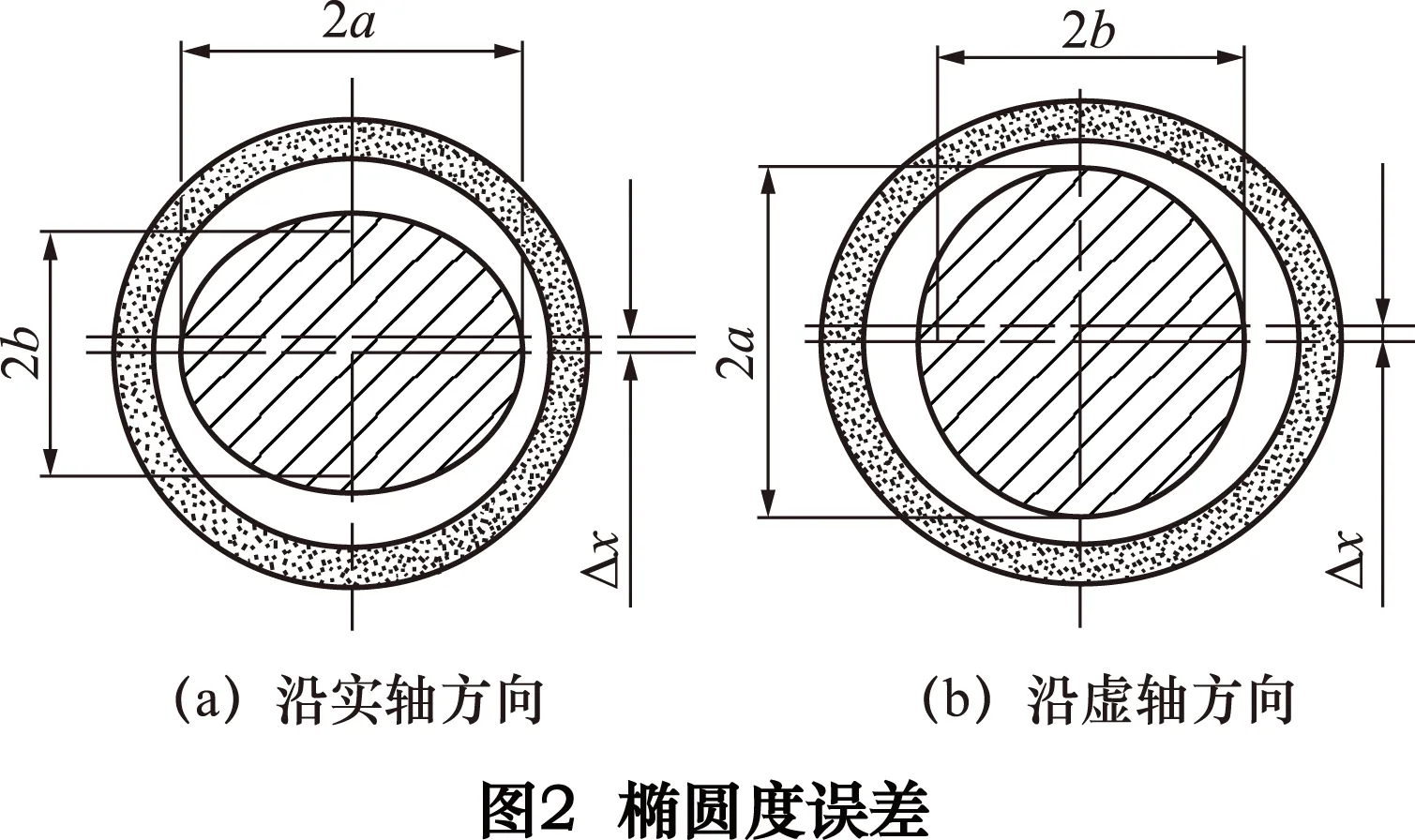
圆度误差主要指椭圆度误差包括沿实轴和虚轴两种模型，如图2所示。

1.1.2圆柱度误差

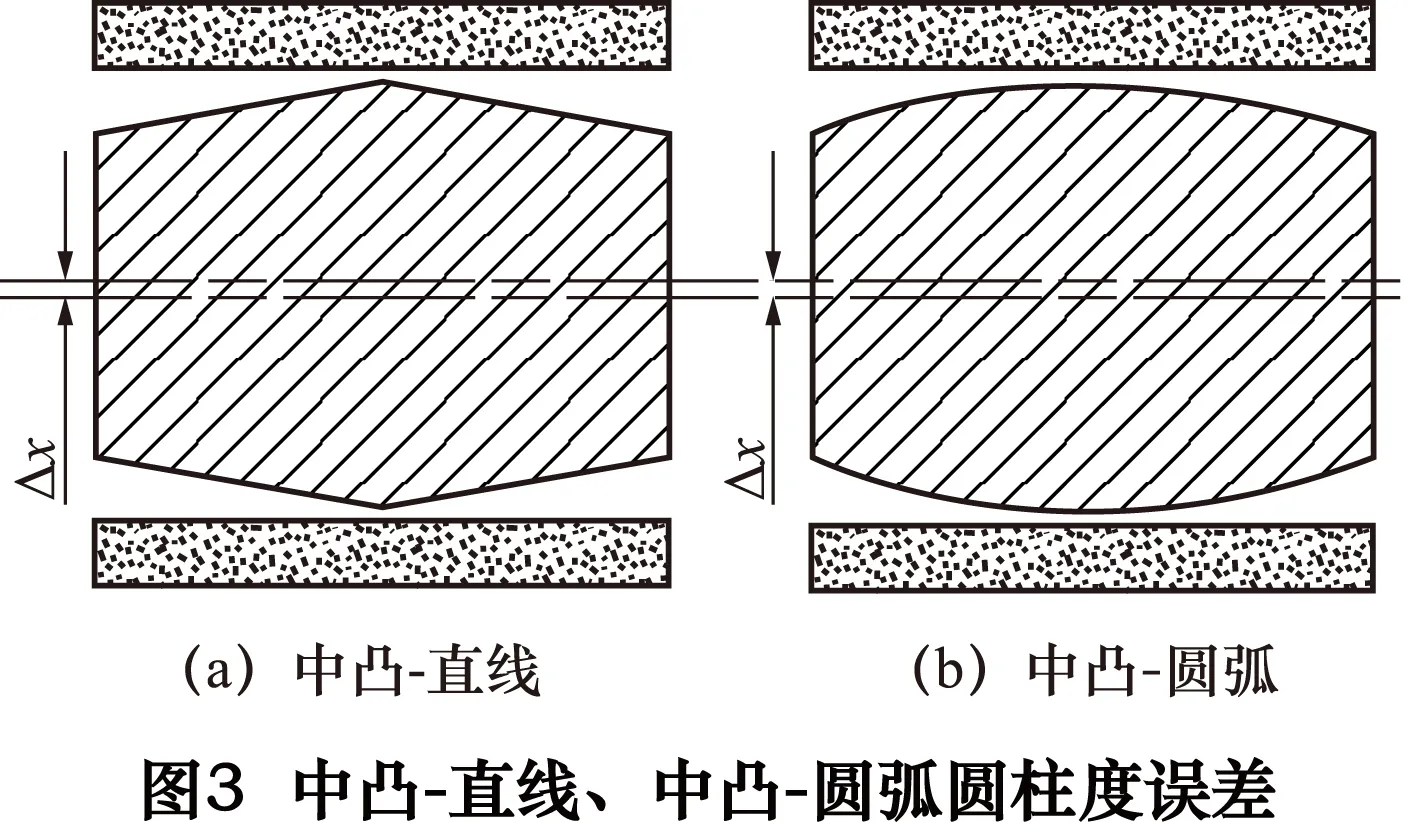
主轴圆柱度误差主要包括中凸、中凹型误差和圆锥度误差，其它形状类型暂不讨论。

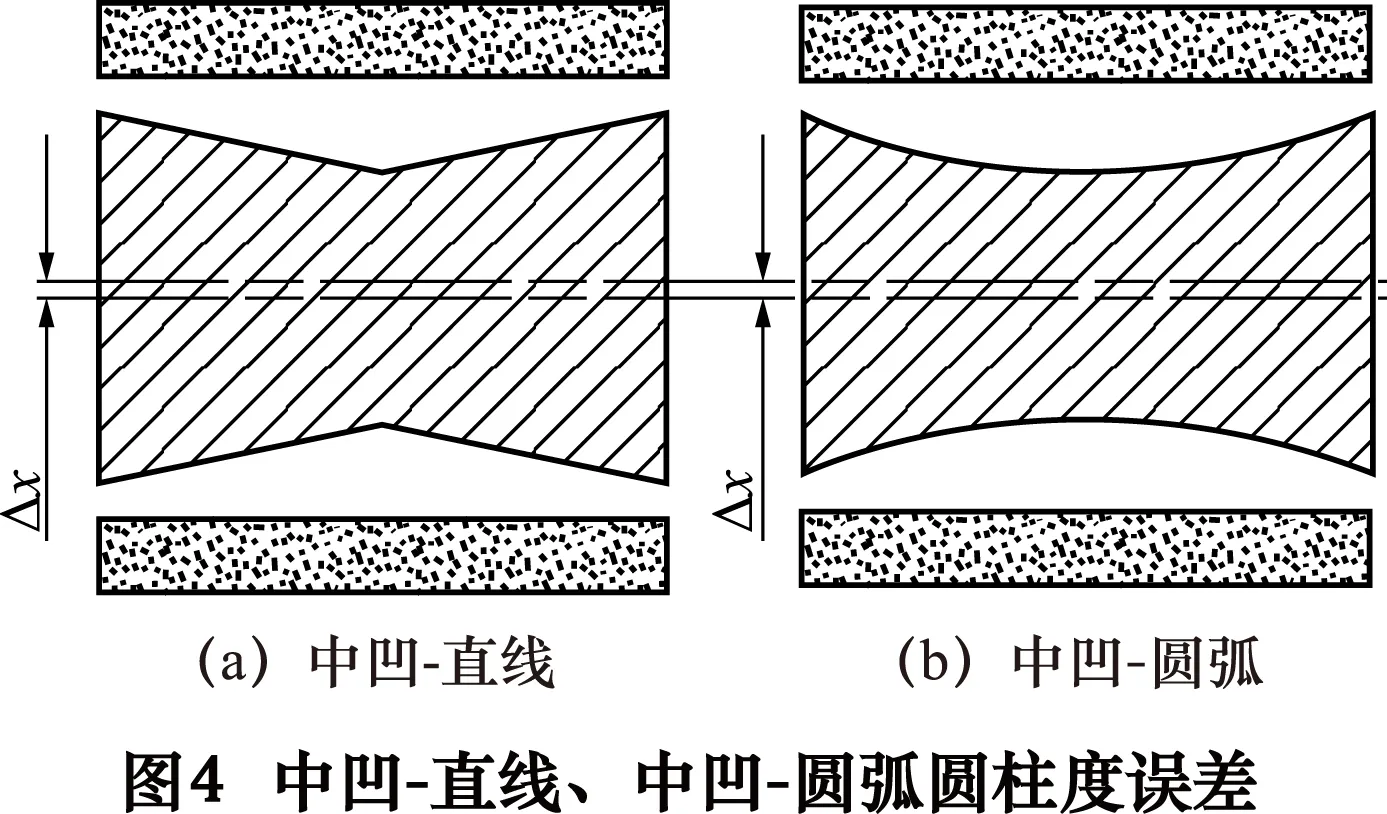
(1)主轴中间凹、凸引起的误差通过最小二乘法拟合为直线形和圆弧形两种，如图3～4所示。

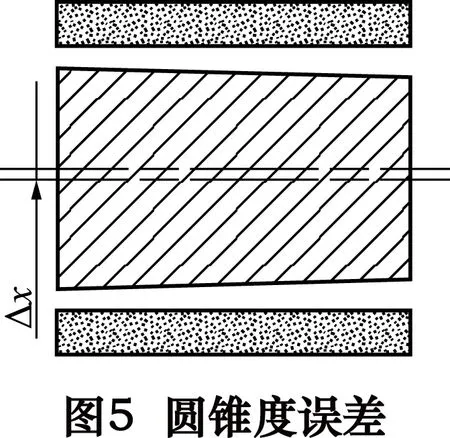
(2)圆锥度误差，造成气膜厚度沿轴线方向的不均匀，如图5所示。

1.1.3倾斜度误差

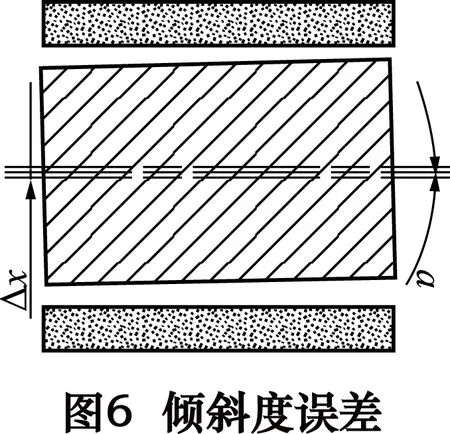
装配过程中主轴倾斜度误差，如图6所示。

1.2网格的划分

通过分析，建立的物理模型包括多孔质气静压径向轴承和气膜间隙两部分，考虑到流场尺寸与气膜尺寸比例失调，计算精度及效率等问题，采用分区划分的方法[13]。对于气膜间隙的厚度方向进行加密处理，两部分均采用结构化网格。本次分析设定气膜间隙网格数值为6，其余部分网格间距为1 mm，多孔质石墨透气率为18%，收敛精度为1×10-9。

1.3边界条件的设置

计算有以下3个假设条件[2]：

(1)壁面绝对光滑，不考虑壁面粗糙度影响。

(2)不考虑转速的影响。

(3)牛顿流体通过多孔介质的流动，假定为层流流动并遵守Darcy定律，不考虑滑移边界的影响。

根据以上假设条件，具体边界条件设定如下：

(1)环境压力Pa=0.1 MPa，环境温度Ta=300 K。

(2)供气压力恒定Ps=0.5 MPa(绝对压力)，供气温度Ts=300 K；出口压力等于环境压力Pa，温度为环境温度Ta。

1.4刚度的求解

多孔质气静压径向轴承的承载能力随着偏心量变化的曲线。对于静态刚度Kw可以采用差分方法进行计算[14]，计算公式如下：

(1)

式中：Kw为静态刚度，N/μm；W为承载力，N；h为气膜厚度，μm。

2　Fluent仿真结果分析

2.1几何误差Fluent分析

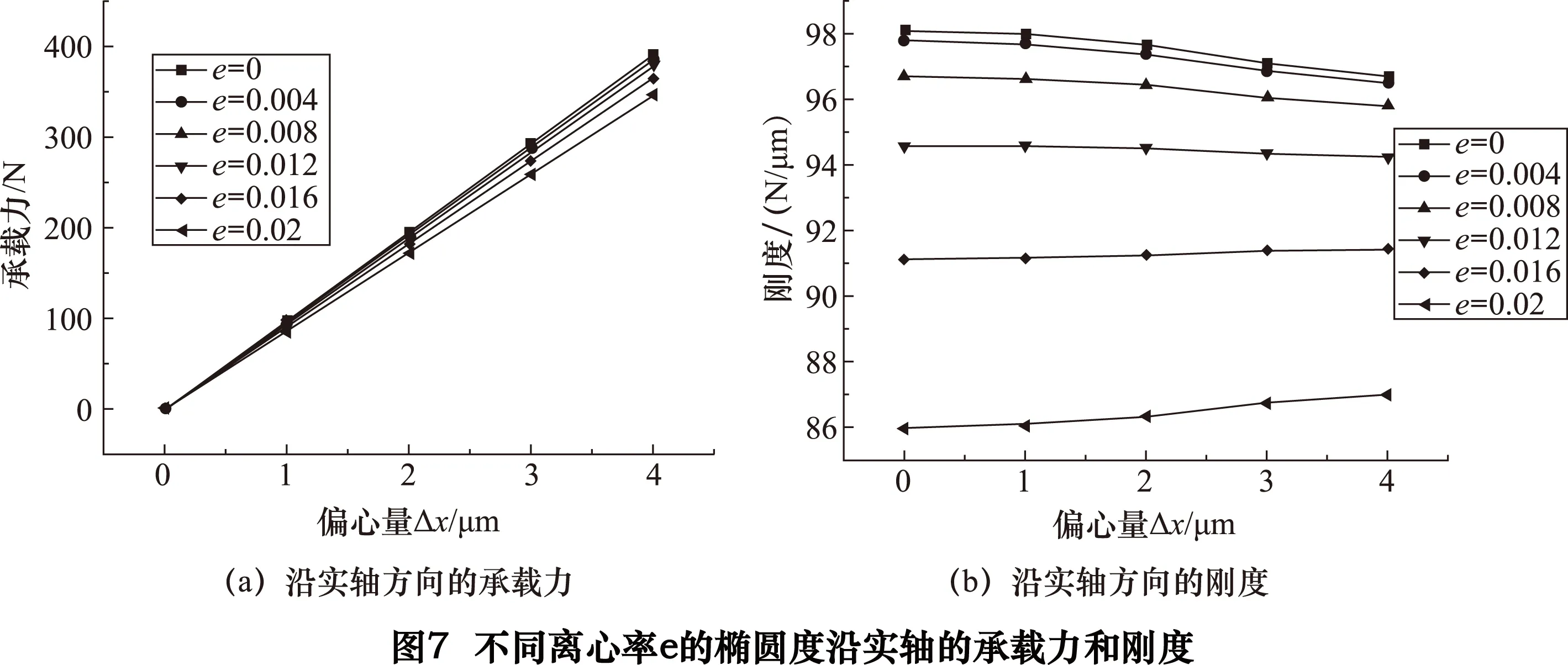
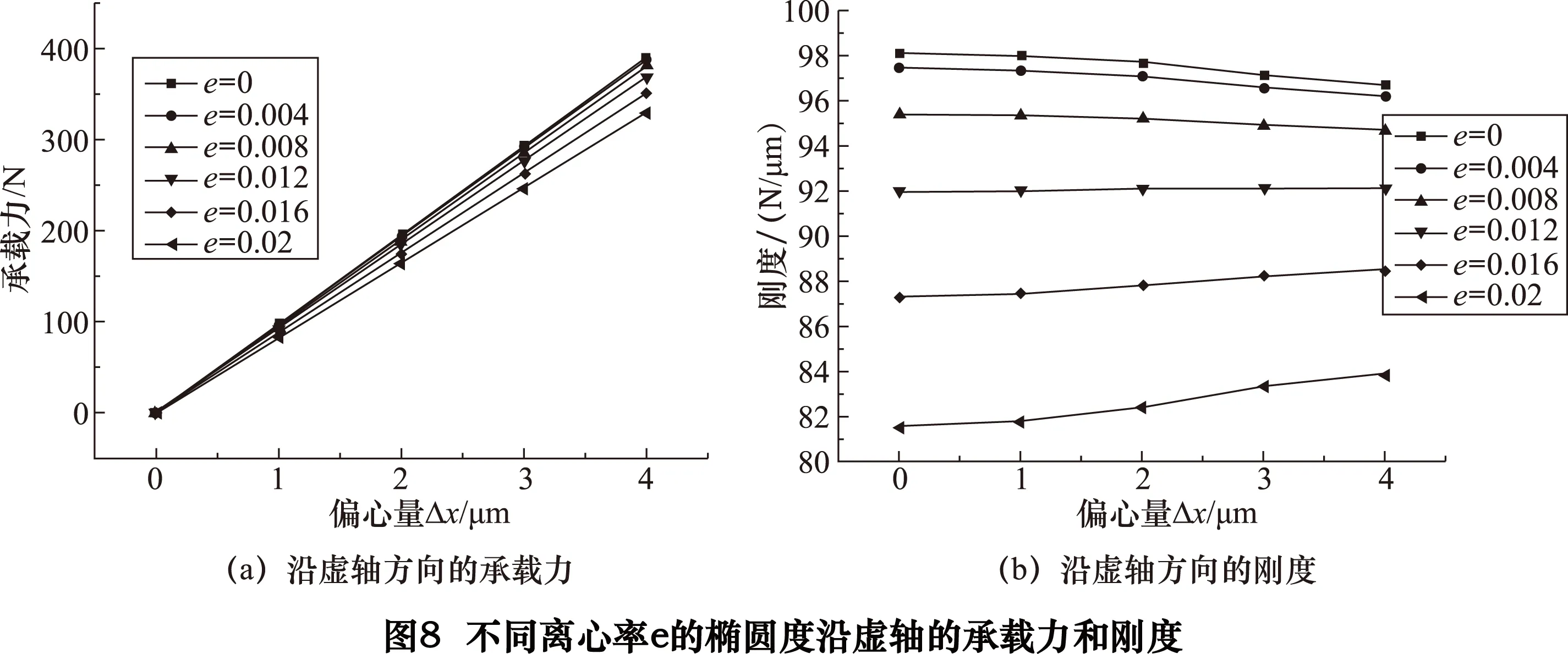
2.1.1椭圆度误差对承载力和刚度的影响分析

不同离心率的椭圆度对承载力和刚度的影响如图7～8所示。

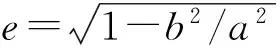
2.1.2圆柱度误差对承载力和刚度的影响分析

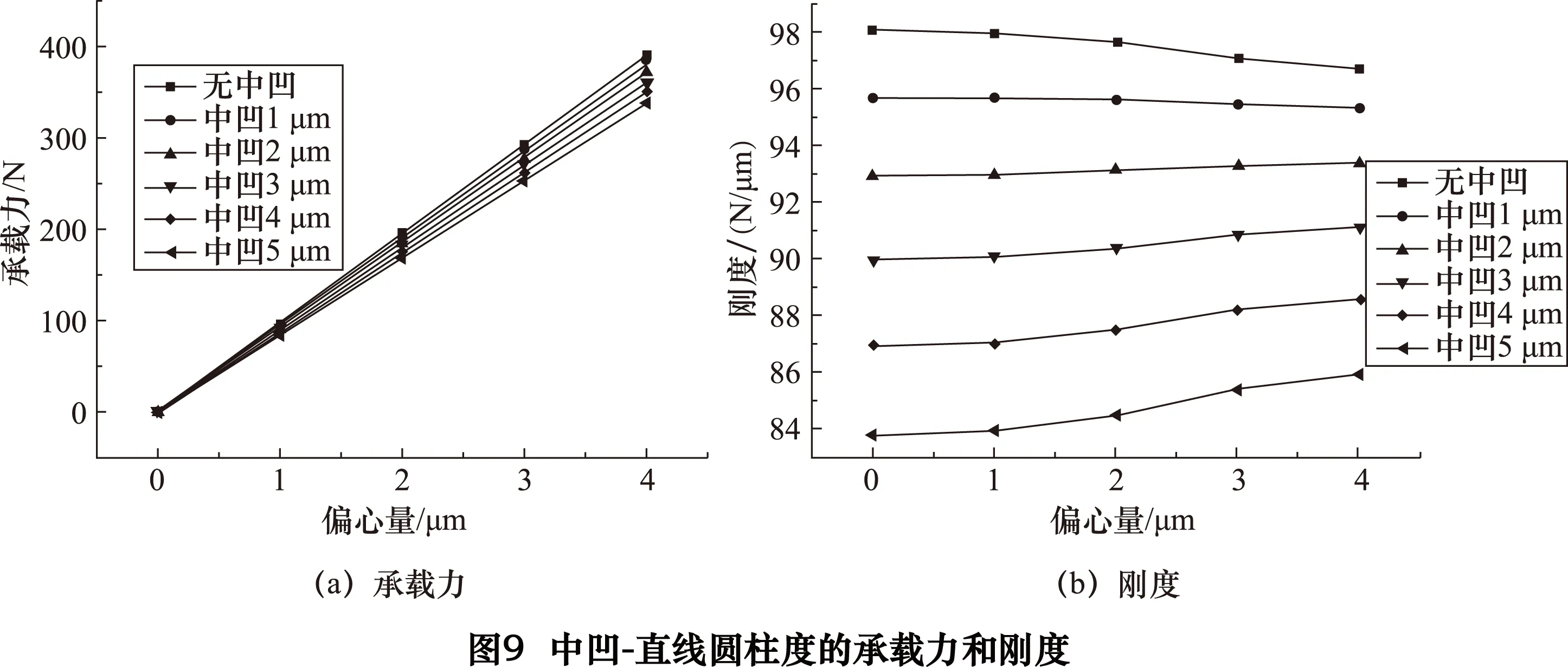
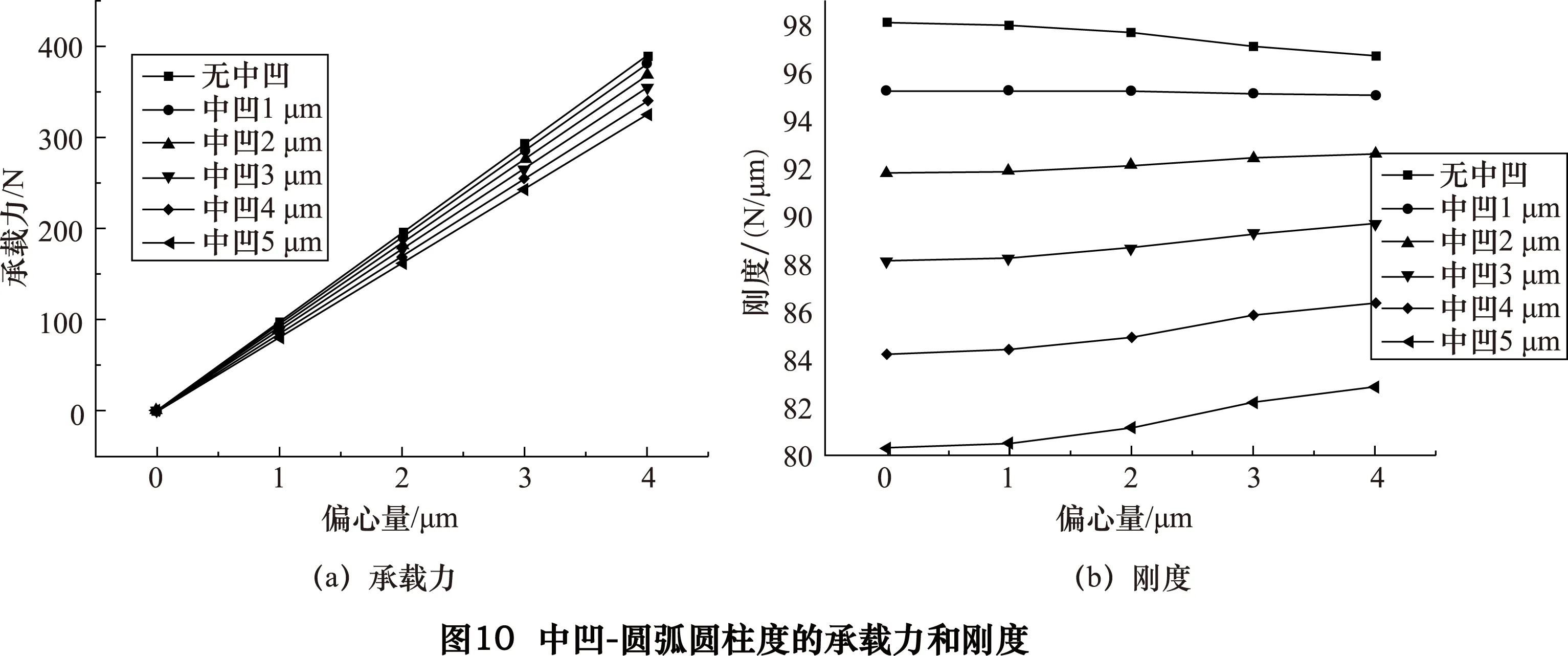
(1)主轴中间凹引起的误差对承载力和刚度的影响如图9～10所示。

在偏心量相同的情况下，随着中凹误差的增大承载力减小；从仿真分析得到的数据比较，中凹-圆弧的承载力(图10a)下降速度比中凹-直线(图9a)的快；

随着中凹误差的增大刚度减小且幅度较大。在相同中凹误差的情况下，随着偏心量的增大承载力增大；随着偏心量的增大刚度小幅度波动；当中凹误差大于1μm时，随着偏心量的增大，刚度增加但幅度较小。中凹-直线(图9)的承载力和刚度整体比中凹-圆弧(图10)的承载力和刚度好；具有中凹-直线(图9)和圆弧(图10)等圆柱度误差的气静压轴承的承载力和刚度比理想情况下差。

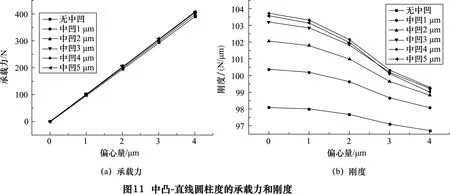
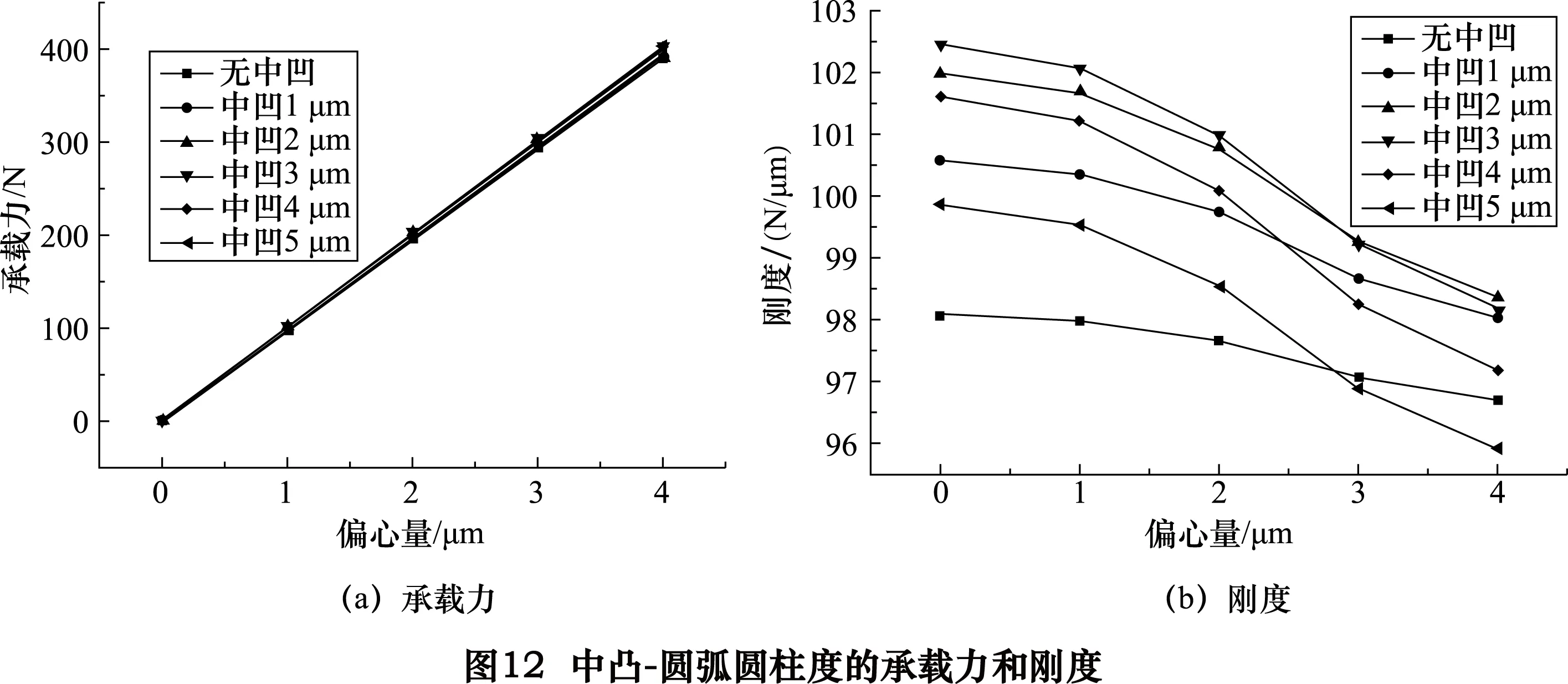
(2)主轴中间凸引起的误差对承载力和刚度的影响如图11～12所示。

在偏心量相同的情况下，随着中凸误差的增大承载力小范围内增加；从仿真分析得到的数据比较，中凸-直线的承载力(图11a)增长速度比中凸-圆弧(图12a)的快；随着中凸误差的增大刚度增大；当中凸误差大于3 μm时，刚度增长幅度较小。在相同的中凸误差情况下，随着偏心量的增大承载力增大；随着偏心量的增大刚度减小；当中凸误差大于3 μm时，刚度减小且幅度较大。中凸-直线(图11)比中凸-圆弧(图12)误差整体的承载力和刚度好。具有中凸-直线(图11)和圆弧(图12)等圆柱度误差的气静压轴承的承载力和刚度比理想情况下的好。

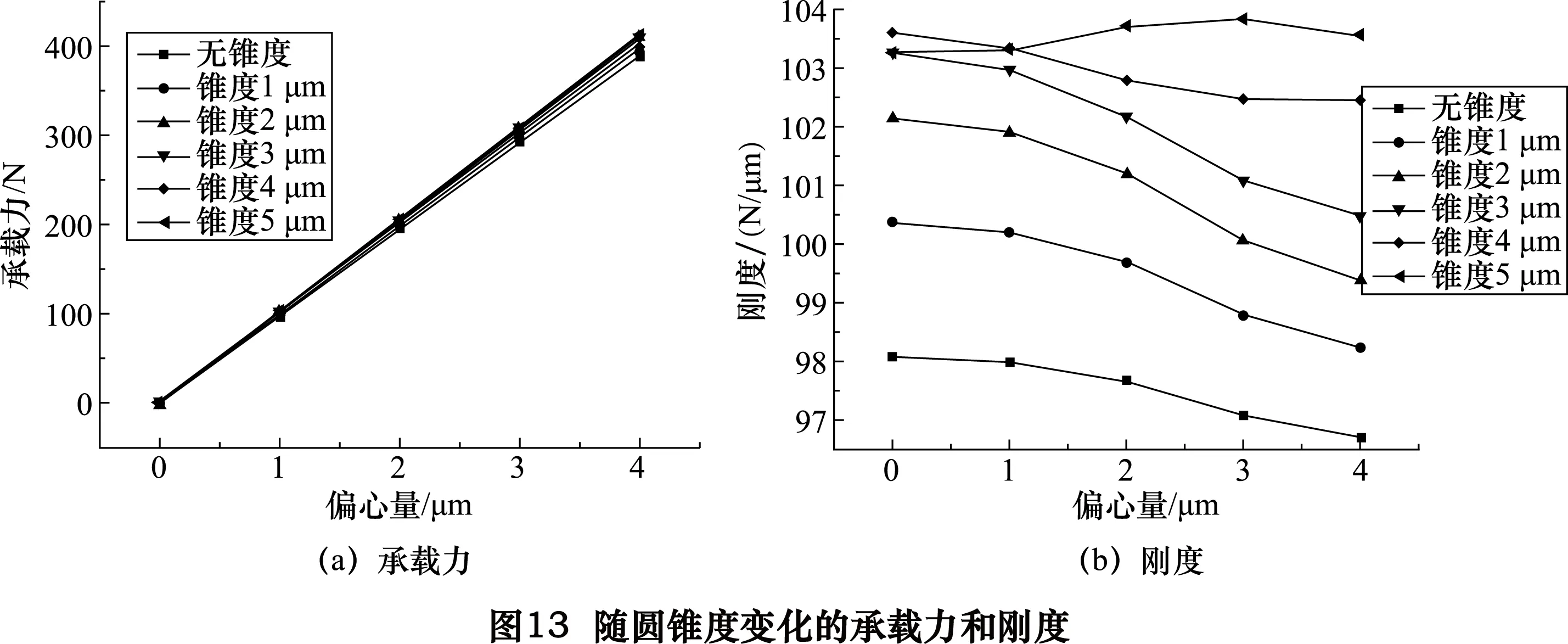
(3)圆锥度对承载力和刚度的影响如图13所示。

在圆锥度相同的情况下，随着偏心量的增大承载力随之增大；刚度随之减小但幅度较小。在偏心量相同的情况下，随着圆锥度误差(图13)的增大承载力和刚度均有不同程度的增加；当圆锥度误差大于3 μm时，刚度增长发生剧变。由于气静压径向轴承副性能不受锥度(正锥或倒锥)的影响，在一定情况下可以允许有一定的圆锥度误差，但应尽量保持在3 μm以内。

2.1.3倾斜度对承载力和刚度影响分析

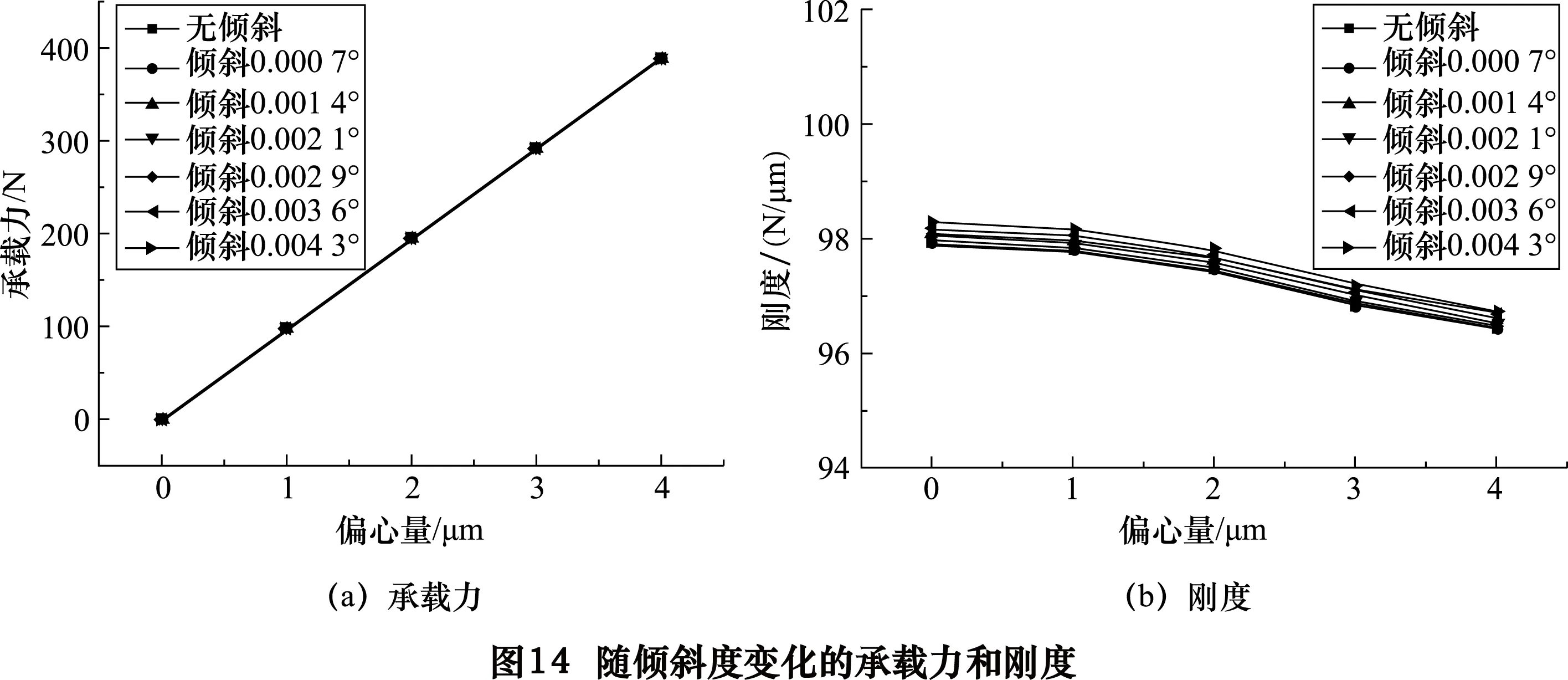
装配中产生的主轴倾斜度引起的位置误差对承载力和刚度的影响，如图14所示。

当0≤α≤arctan(0.006/L)时，在倾斜度(图14)相同的情况下，随着偏心量的增大刚度减小但幅度较小。在偏心相同的情况下，随着倾斜角度的变化承载力和刚度几乎不变；沿径向方向上倾斜在3 μm以内时，对气静压轴承的性能影响不大。

2.2原因分析

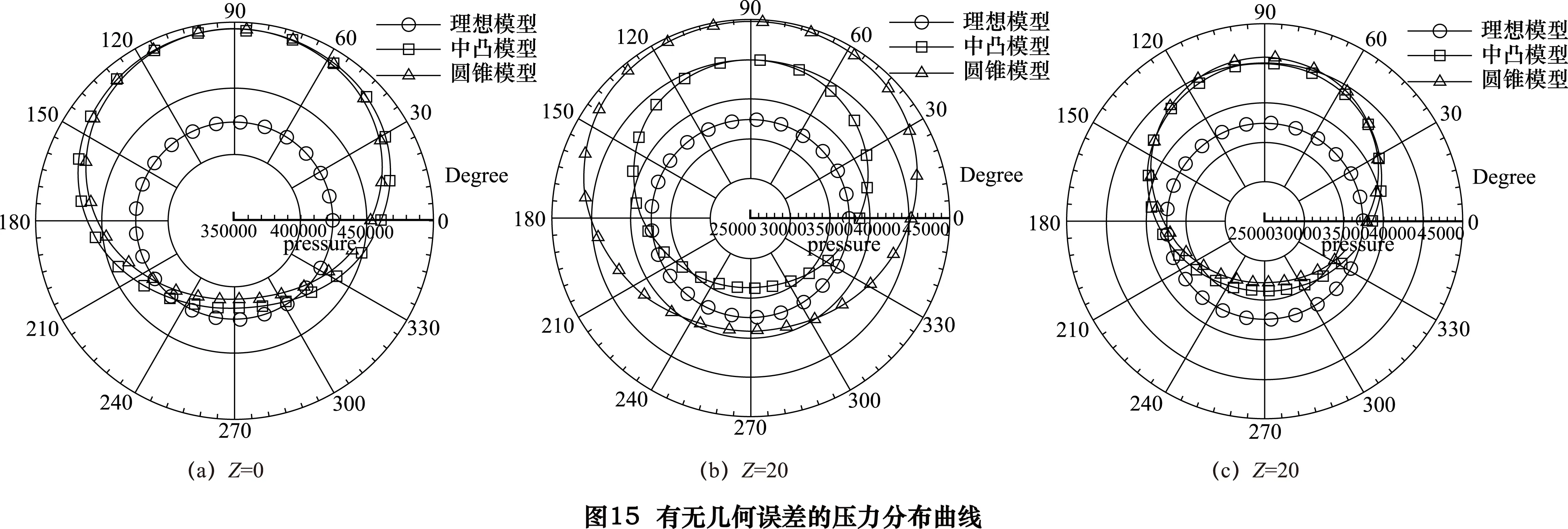
多孔质气静压主轴具有中凸圆柱度和圆锥度几何误差时，承载力和刚度反而增大主要是由于几何误差作用促使气膜间隙沿轴向和径向都不均匀而产生的压力分布不均，如图15所示。

图15中，90°方向为气膜间隙较小一侧；270°方向为气膜间隙较大一侧；Z=0(图15a)处为轴向中间位置；Z=-20(图15b)和Z=20(图15c)分别为轴向1/4和3/4处。气体通过多孔质气静压轴承进入孔/轴之间形成的气膜间隙，90°方向压力最大，270°方向压力较小。理想模型压力分布沿轴向在小范围内波动，在轴向对称位置的压力分布相等，沿径向形成的压差约为供气压力的10%；中凸模型由于几何误差的作用，在轴向Z=0处时，气膜间隙最小从而导致在径向90°方向压力最大；在轴向Z=-20和Z=20时，气膜间隙逐渐增大，压力分布逐渐减小，沿径向形成的压差约为供气压力的31%；圆锥模型(正锥)由于几何误差的作用，在轴向Z=-20处时，气膜间隙较小，压力分布较大；在轴向Z=20处时，气膜间隙逐渐增大，压力分布逐渐减小，沿径向形成的压差约为供气压力的34%；中凸和圆锥模型在轴向1/4和3/4处，沿径向压差比理想模型的大，所以中凸和圆锥模型承载力和刚度增加。由于圆锥模型沿径向压差比中凸模型的大，所以在相同圆柱度误差值下，随着偏心量的增大，圆锥模型刚度减小幅度比中凸模型小。最终，气体沿着具有中凸圆柱度和圆锥度等几何误差的主轴线性流向两端。

3　结语

本文研究了几何误差对多孔质气体静压轴承副的特性影响，得到如下结论：

(1)具有中凸和圆锥度误差的气静压轴承的承载力和刚度比理想情况下要好，可以允许有一定的中凸和圆锥度误差，但应尽量在3 μm以内。

(2)具有椭圆度和中凹圆柱度误差的气静压轴承的承载力和刚度比理想情况下差；生产中应尽量避免主轴有椭圆度和中凹误差。

(3)沿椭圆实轴的气静压轴承承载力和刚度比沿椭圆虚轴的好。

(4)沿径向方向上倾斜3 μm以内时，对气静压轴承的性能影响不大。

[1]杜金名. 多孔质流体静压轴承润滑技术的研究[D]. 哈尔滨：哈尔滨工业大学，2003.

[2]王云飞. 气体润滑理论与气体轴承设计[M]. 北京：机械工业出版社，1999.

[3]吴笛. 局部多孔质气体静压径向轴承的建模与仿真[J]. 轴承，2010(10)：31-36.

[4]李欢欢，于贺春，张国庆，等. 椭圆误差对多孔质径向气体静压轴承特性的影响[J]. 制造技术与机床，2015(6)：84-87.

[5]李树森，刘暾，张鹏顺，等. 几何形误差对气体静压圆柱轴承运动精度的影响[J]. 润滑与密封，2001(3)：45-48.

[6]徐建民，陈明. 形状误差对气体静压圆柱轴承静特性的影响[J]. 武汉化工学院学报，1998，20(1)：71-74.

[7]侯志泉. 基于CFD动网格方法的液体静压主轴回转精度机理研究[D]. 长沙：湖南大学，2013.

[8]边新孝，李谋渭，李威. 加工误差对气体静压径向轴承的影响[J]. 北京科技大学学报，2005，27(3)：331-333.

[9]边新孝，李谋渭. 静压空气轴承偏载时的承载分析[J]. 航空精密制造技术，2005，41(1)：17-19.

[10]Pande S S, Somasundaram S. Effect of manufacturing errors on the performance of aerostatic journal bearings[J]. Wear, 1981，66(2)：145-156.

[11]James Nevel. The effect of stator and rotor form error on air bearing spindle accuracy[D]. US:The pennsylvania state university, 2011.

[12]毛平淮. 互换性与测量技术基础[M]. 北京：机械工业出版社，2011.

[13]Liang Yingchun, Liu Jingshi. Computational fluid dynamics analysis of an aerostatic journal bearing with slot-entry restrictors[J]. Advanced Science Letters, 2011，4(8-10)：2817-2821.

[14]孙雅洲，卢泽生，饶河清. 基于FLUENT软件的多孔质静压轴承静态特性的仿真与实验研究[J]. 机床与液压，2007，35(3)：170-172.

(编辑谭弘颖)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Effect of geometric error on the performance of porous aerostatic bearing

HOU Xiaoshuai, ZHAO Zexiang, YU Hechun, ZHANG Guoqing, HE Xin, YAO Bo

(School of Mechanical & Electrical Engineering，Zhongyuan University of Technology, Zhengzhou 451191，CHN )

The effect of geometric error on the performance of porous aerostatic bearing is studied in this paper. The three-dimensional models of porous aerostatic bearing are built and the simulations are carried out with the Fluent software based on the finite volume method. The influence of the capacity and stiffness of porous aerostatic bearing are obtained; the distribution of uneven pressure caused by gas film clearance changes, error within 3μm of conicity and bulge in the middle can improvement the performance of porous aerostatic bearing; within 3μm of slope on the radial direction has a little influence; error of ovality and concave have a negative effect on the performance of porous aerostatic bearing.

aerostatic bearing；geometric error；loading capacity；stiffness

TH133.35

A

10.19287/j.cnki.1005-2402.2016.07.004

侯晓帅，男，1990年生，硕士研究生，主要研究方向为精密制造技术与装备。

2016-01-26)

160713