PMMA微细铣削参数优化实验研究*

李元镇　程　祥　孟繁杰　郑光明　徐汝锋

(山东理工大学机械工程学院，山东 淄博 255049)



PMMA微细铣削参数优化实验研究*

李元镇程祥孟繁杰郑光明徐汝锋

(山东理工大学机械工程学院，山东 淄博 255049)

以聚合物微流体装置中常用的基体材料PMMA作为对象，通过高速微细铣削实验，对铣削过程中的因素参数进行优化实验研究。利用单因素实验法和正交实验法，以被加工工件的表面粗糙度为实验指标，选取轴向切深、每齿进给量和径向切深3个主要因素展开实验。实验结果表明，轴向切深ap=15 μm，每齿进给量fz=5 μm/z，径向切深ae=0.34 mm时，可以获得最小的表面粗糙度。对表面粗糙度影响程度由大到小依次是ap、fz、ae，并进一步通过实验验证。

PMMA；微细铣削；参数优化；单因素实验；正交实验

材料PMMA(聚甲基丙烯酸甲酯)由于透明度优良，具有良好的绝缘性、耐腐蚀性和机械强度，使其在航空、建筑、农业、光学仪器等领域得到了广泛应用[1]。同时，由于良好的光学特性，PMMA已经成为聚合物微流体装置研究中的主要基体材料。利用微细铣削的加工方法加工PMMA基体材料，可以提高加工过程的效率，减少加工成本，而且适合加工复杂的三维形貌特征[2]。但是对PMMA材料的微细铣削研究尚处于探索阶段，因此对其进行微细铣削实验研究具有重要的研究价值。

微细铣削是微细加工领域的一种精密加工方法，以其加工精度高、成型能力强[3]成为微机械制造领域中的关键技术。与常规尺度机械加工相比，微细铣削伴有最小切削厚度现象，从而出现尺度效应，这使得微细铣削规律不同于常规的铣削[4]。在微细铣削中，表面粗糙度是高速精加工表面质量指标中的一个重要评价参数[5]，而在影响表面粗糙度的因素中，铣削用量轴向切深、每齿进给量和径向切深对加工表面质量起主要影响作用，因此铣削过程中各因素参数的合理选取与优化显得至关重要。针对不同材料的微细铣削，国内在因素参数优化研究上做了一系列的实验，文献[6]分别针对不锈钢和生物材料钛做了关于主轴转速、切削深度和每齿进给量对表面粗糙度的影响实验，结果表明高的主轴转速可以获得更好的加工质量。文献[7]对铝合金材料研究分析了切削速度与每齿进给量交互作用对加工槽底表面粗糙度的影响，实验结果表明当每齿进给量较小时，随着切削速度的提高表面粗糙度值呈先减小后增大的变化趋势；而每齿进给量较大时，随切削速度的提高表面粗糙度值先增大后减小。切削速度较低时，表面粗糙度值随每齿进给量的增大先减小后增大；但切削速度大于30 m/min 时，随着每齿进给量的增大，表面粗糙度值呈现逐渐增大的趋势。

本文针对PMMA材料，通过高速微细铣削实验，并借助单因素实验法和正交实验法[8]，研究微细铣削表面粗糙度以及各铣削因素对其影响规律，获得微细铣削的优化因素参数。

1　实验准备

本实验加工机床采用三坐标桌面微细铣削数控机床3A-S100，如图1所示，具有 0.5 μm的定位精度[9]。机床主轴采用80 000 r/min的高速空气轴承和空气涡轮驱动主轴，径向跳动和轴向窜动均在1 μm以内。

本实验采用直径为1 mm的涂层双刃硬质合金立铣刀，所用加工PMMA材料工件为长30 mm、宽30 mm、高20 mm的长方体块。

2　实验方案与结果分析

在PMMA微细铣削参数优化实验研究中，实验的目的是获取微细铣削中的最优铣削因素参数，实验指标为实验后测量的表面粗糙度，选取的铣削因素是轴向切深ap(背吃刀量)、每齿进给量fz和径向切深ae(侧吃刀量)。先采用单因素实验法获得适合铣削的各种因素的参数范围，然后在其所在的适当范围内各取水平值进行正交实验，以此确定铣削过程中各因素的影响大小及显著性，寻找微细铣削中的最优铣削参数组合。

2.1微细铣削单因素实验

单因素实验选取的各铣削因素如表1所示。

由表1可以看出，共需铣削18个沟槽表面。为了减少多次装夹带来的刀具与工件之间的定位误差，安排的实验布局如图2所示。

表1　实验各铣削因素参数

在本铣削实验中，由于第一组变量因素为轴向切深，第二组变量因素为每齿进给量，故两组实验每个沟槽均可由铣刀一次单向进给铣削完成，即沟槽的宽度就是铣刀的直径1 mm，如图3a所示。第三组变量因素为径向切深，因为刀具需要进行径向进给，故每个沟槽由铣刀一次往复进给铣削完成，如图3b所示。由于本实验中轴向切深即背吃刀量较小，为了便于实验后续表面粗糙度的测量，实验中每个沟槽均轴向下刀2次，即每个沟槽连续下刀2次进行铣削。

实验加工过程及结果如图4所示，测量时使用接触式表面粗糙度测量仪，采用每组实验各测量4次表面粗糙度取平均值的方法，从而对铣削后的各个沟槽的表面粗糙度值进行分析。

第一组实验结果如图5所示。

由图5可看出随着轴向切深的不断变大，表面粗糙度值呈现先减小后增大的趋势。轴向切深在15 μm时表面粗糙度值达到最小，当轴向切深小于15 μm时，由于最小切削厚度的影响，表面粗糙度值随着轴向切深的减小而增大；当轴向切深大于15 μm时，随着轴向切深的不断增大，刀具在铣削过程中所受到的切削力越大，产生的振动越大，表面质量变差，从而表面粗糙度值逐渐增大。因此在进行下一步的微细铣削正交实验时，轴向切深可在区间10～20 μm内取值，从而得到更小的表面粗糙度值。

第二组实验结果如图6所示。

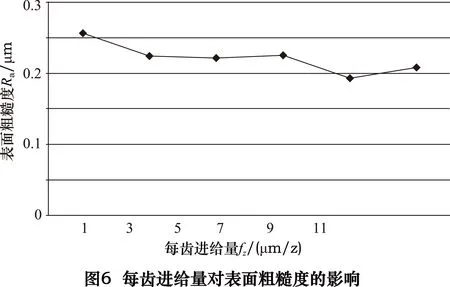
由图6可以看出随着每齿进给量的不断变大，表面粗糙度值总体呈现逐渐减小的趋势。当每齿进给量fz=7 μm/z与fz=9 μm/z时图像折线波动较大，此时图像不稳定可能是实验测量误差造成的。在本组实验中，虽然每齿进给量fz=9 μm/z时表面粗糙度最小，但此时沟槽毛刺较严重(如图7所示，图中各沟槽从左往右每齿进给量fz依次为1 μm/z，3 μm/z，5 μm/z，7 μm/z，9 μm/z，11 μm/z)。而每齿进给量fz=5 μm/z时，沟槽毛刺较少，表面粗糙度值也较小，因此在下一步的正交实验中每齿进给量fz可在5 μm/z附近范围内取值，从而得到更小的表面粗糙度值。

第三组实验结果如图8所示。

由图8可看出随着径向切深的不断增大，表面粗糙度值呈现缓慢增大的趋势，特别是径向切深在0.2～0.4 mm范围时表面粗糙度值变化并不显著。因此在进行下一步的微细铣削正交实验时，径向切深可根据实际情况在0.2～0.4 mm范围内取值，从而得到更小的表面粗糙度值。

通过以上实验结果分析可以得出，在单因素实验中当其他因素不变，轴向切深ap=15 μm时，沟槽的表面粗糙度达到最小值；当其他因素不变，径向切深ae=0.3 mm时，沟槽的表面粗糙度达到最小值；当其他因素不变，每齿进给量fz=9 μm/z时，沟槽的表面粗糙度达到最小值，但每齿进给量fz=5 μm/z时，沟槽毛刺较少，表面粗糙度值也较小。因此在下一步的正交实验中每齿进给量fz可在5 μm/z附近范围内取值，而轴向切深ap可在15 μm附近范围内取值，径向切深ae可在0.3 mm附近范围内取值。综合来看，正交实验中轴向切深ap可在10～20 μm范围内取值，每齿进给量fz可在3～7 μm/z范围内取值，径向切深ae可在0.2～0.4 mm范围内取值。

2.2微细铣削正交实验

基于单因素实验结果，正交实验3个主要影响因素及水平如表2所示。

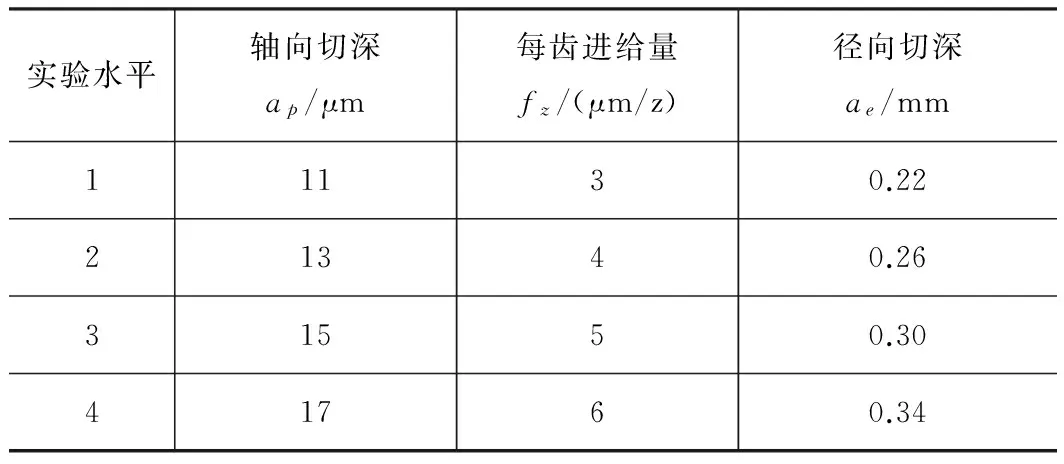
表2　实验主要影响因素及水平

因为本实验仅考察3个主要因素对表面粗糙度的影响效果，不考察因素间的交互作用，故选用L16(45)正交表，具体实验方案如表3所示。

表3　实验具体铣削方案

由表3可以看出，该实验共需铣削16个沟槽表面。为了减少多次装夹带来的刀具与工件之间的定位误差，安排的实验布局如图9所示。

因为本实验是多因素正交实验，在每个沟槽的铣削过程中，轴向切深、每齿进给量和径向切深3个因素需同时考虑，所以每个沟槽由铣刀一次往复进给铣削完成，如图10所示。同样为了便于实验后续表面粗糙度值的测量，实验中每个沟槽均轴向下刀4次，即每个沟槽连续下刀4次进行铣削。

实验采用每组实验各测量4次表面粗糙度取平均值的方法，基于表3所列的各种不同铣削参数组合，所测得的各个沟槽的表面粗糙度值如图11所示。

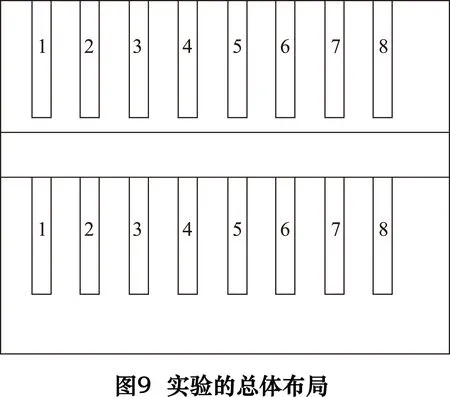
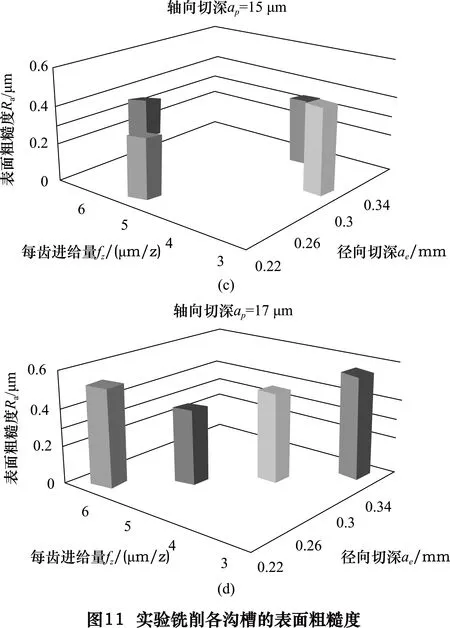
对图11中的实验数据进行极差分析，分析结果如表4所示。

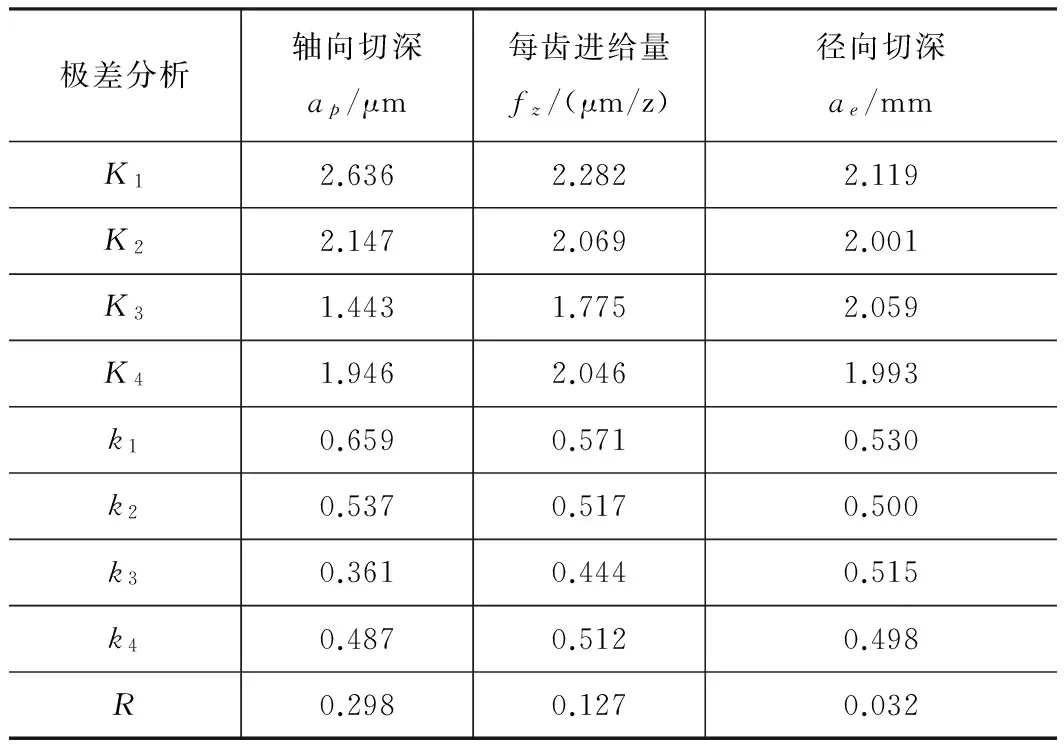
表4　实验数据的极差分析

表中：Ki为因素所在列第i水平对应的粗糙度之和；ki为因素所在列第i水平对应的粗糙度的平均值；R为各列因素所对应的极差值

根据极差R的大小，可以判断各因素对实验指标的影响主次。由表4比较各R值大小，可得0.298>0.127>0.032，所以在本实验中，对表面粗糙度影响最大的因素是轴向切深ap，其次是每齿进给量fz，影响最小的因素是径向切深ae。同时以各因素水平为横坐标，表面粗糙度的平均值ki为纵坐标，可绘制各因素与表面粗糙度的趋势图，如图12所示。

由图12a可以看出，随着轴向切深的增大，表面粗糙度值呈现先减小后增大的趋势，轴向切深在拐点处时表面粗糙度值最小，变化趋势非常明显；图12b中随着每齿进给量的增大，表面粗糙度值呈现先减小后增大的趋势，每齿进给量在拐点处时表面粗糙度值最小，变化趋势较明显；图12c中随着径向切深的增大，表面粗糙度值变化较缓和，变化趋势不明显。

根据图11对实验数据进行方差分析，分析结果列于方差分析表中，如表5所示。

表5　实验数据的方差分析

表中：A为轴向切深ap，B为每齿进给量fz，C为径向切深ae，SS为离差平方和，df为自由度，MS为平均离差平方和。

通过以上实验结果分析可以得出，由于本实验的指标为铣削后的表面粗糙度值，实验指标越小,表面质量越好。从表4和图12中可以看出，在不考虑交互作用的情况下，最优方案应取各因素最小k值所对应的水平，即轴向切深ap=15 μm，每齿进给量fz=5 μm/z，径向切深ae=0.34 mm。从方差分析结果表5可以看出，轴向切深ap对实验结果有非常显著的影响，每齿进给量fz对实验结果有显著影响，径向切深ae对实验结果没有显著影响，所以对于因素径向切深来说，可以选取其中最大的水平值ae=0.34 mm，从而在实际铣削加工中提高铣削效率，节省加工时间。

3　实验验证

按照所得最优方案的铣削参数，即轴向切深ap=15 μm，每齿进给量fz=5 μm/z，径向切深ae=0.34 mm分别进行4组验证实验，结果如图13所示，表面粗糙度值测量结果如表6所示。

表6　验证实验的测量结果

从表6中的测量数据可以看出，最优方案的铣削参数即轴向切深ap=15 μm，每齿进给量fz=5 μm/z，径向切深ae=0.34 mm时可以获得较小的表面粗糙度值，从而验证了上述理论分析的正确性以及本实验最优方案铣削参数的可行性。

根据本实验所得到的最优铣削参数可以铣削形状较为复杂的沟槽特征，从而获得较小的表面粗糙度值，铣削的沟槽特征如图14所示。

4　结语

对PMMA材料进行了微细铣削的单因素实验和正交实验研究，经过对实验数据的综合分析，可以得出以下结论：各因素对表面粗糙度影响程度由大到小依次是轴向切深ap、每齿进给量fz和径向切深ae。轴向切深和每齿进给量对实验结果有显著的影响，随着轴向切深和每齿进给量分别增大，表面粗糙度值呈现先减小后增大的趋势，轴向切深和每齿进给量与表面粗糙度之间存在一个近似抛物线曲线关系。径向切深对实验结果没有显著的影响，随着径向切深的增大，表面粗糙度值变化较缓和，变化趋势不明显。得到了优化的各因素参数为轴向切深ap=15 μm，每齿进给量fz=5 μm/z，径向切深ae=0.34 mm。

[1]陈卢松, 黄争鸣. PMMA透光复合材料研究进展 [J]. 塑料, 2007, 36(4): 90-91.

[2]Chen P C, Pan C W, Lee W C, et al. An experimental study of micromilling parameters to manufacture microchannels on a PMMA substrate[J]. Int J Adv Manuf Technol, 2014, 71: 1623-1630.

[3]李洪波, 文杰, 李红涛. 微铣削表面粗糙度实验研究 [J]. 武汉理工大学学报, 2010, 32(14): 187-188.

[4]石文天, 刘玉德, 王西彬, 等. 微细铣削表面粗糙度预测与试验[J]. 农业机械学报, 2010, 41(1): 211-215.

[5]王素玉, 艾兴, 赵军, 等. 高速铣削表面粗糙度建模与预报[J]. 制造技术与机床, 2006(8): 65-68.

[6]Elisa V, Xavier G, Joaquim C. An experimental analysis of process parameters for the milling of micro-channels in biomaterials[J]. International Journal of Mechatronics and Manufacturing Systems, 2012, 5(1): 46-49.

[7]邢栋梁, 张建华, 沈学会, 等. 微细铣削铝合金表面粗糙度的实验研究 [J]. 制造技术与机床, 2011(3): 30-33.

[8]李云雁, 胡传荣. 试验设计与数据处理 [M]. 北京: 化学工业出版社, 2008: 128-153.

[9]张升, 程祥, 代玉娟. 超精密桌面微细铣削机床的研制 [J]. 机械设计与制造, 2014(1): 110-112.

(编辑李静)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

An experimental study on micro-milling parameters optimization of PMMA

LI Yuanzhen, CHENG Xiang, MENG Fanjie, ZHENG Guangming, XU Rufeng

(School of Mechanical Engineering, Shandong University of Technology, Zibo 255049, CHN)

In this paper, the substrate material PMMA which is widely used in the polymer microfluidic devices is selected to study for the parameters optimization by high speed micromilling experiments. The experiments have been studied by using single factor experiment method and orthogonal experiment method. The axial depth of cut, the feed per tooth and the radial depth of cut have been selected as the main factors in the experiments of micromilling according to the milled surface roughness. The experiment results show that the smallest surface roughness is achieved with the axial depth of cut of 15 μm, feed per tooth of 5 μm/z and radial depth of cut of 0.34 mm. The impact of surface roughness in descending order isap,fz,ae.Further verification experiments have been successfully conducted.

PMMA; micromilling; optimization of parameters; single factor experiment; orthogonal experiment

TG547

A

李元镇，男，1991年生，学士，研究方向为微细铣削加工。

2015-07-21)

160206

* 山东省自然科学基金(ZR2015EL023)